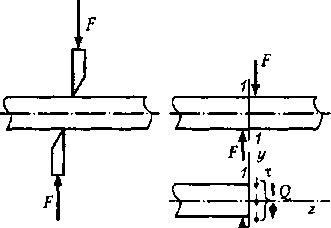Как найти площадь среза

Срез металла

Срез металла, его толщина, ширина и площадь. Вследствие деформации  стружки, происходящей в процессе ее образования, ширина и особенно толщина ее получаются больше размеров b и а на рис. Длина стружки оказывается меньше соответственного размера обработанного участка поверхности детали. Поэтому площадь 1, заштрихованная на рис. и называемая срезом, не отражает поперечного сечения стружки, снимаемой в этом случае.

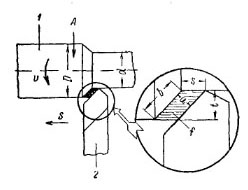
Срезом металла называется поперечное сечение слоя металла, снимаемого при данной глубине резания и подаче. Размеры среза характеризуются его толщиной и шириной.

Толщиной среза металла называется расстояние между положениями режушей кролхки резца до и после одного оборота детали, измеренное по перпендикуляру к режущей кромке.

Толщина среза измеряется в миллиметрах  (мм) и обозначается буквой а.
Шириной среза называется расстояние между крайними точками работающей части режущей кромки резца. Ширина среза измеряется в миллиметрах (мм) и обозначается буквой Ь.
Четырехугольник, заштрихованный на рис., изображает площадь среза.

Площадь среза равна произведению подачи на глубину резания.

Площадь среза измеряется в миллиметрах квадратных и обозначается буквой f определяется по формуле среза металла:

f=s*t

где f — площадь в мм²;

s – подача на один оборот в мм;

t – глубина резания в мм.

Если, например, обтачивание детали производится при подаче 0,2 мм/об и глубине резания 4 мм, то площадь среза равна

f=s*t=0,2*0,4=0,8 мм²

Инструкционно-технологическая
карта

к
практическому занятию №2

Дисциплина:
Техническая
механика

Тема: Расчет на
срез и смятие.

Цель
занятия: Закрепить
теоретический материал по последовательности расчетов на срез и смятие.

Отводимое время: 2ч.

Обеспечение рабочего места:

1. рабочая тетрадь.

2. инструкционно-технологическая карта.

3. чертежные принадлежности.

Содержание
работы:

1. Ознакомиться с заданиями и методическими указаниями по их
выполнению.

2. Выполнить расчеты.

3. Выполнить задание по определить, исходя из
условий прочности на срез и смятие, необходимый диаметр болта в соединении.

ЗАДАНИЯ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ИХ
ВЫПОЛНЕНИЮ

1. общие сведения.

Срезом называется
деформация, возникающая под действием двух близко расположенных противоположно
направленных сил. При этом возникают касательные напряжения.

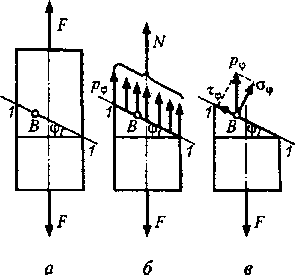
Примером  элемента
металлических конструкций,  работающего на срез,  служит заклёпка (рис.а).  При
некоторой величине действующих сил F
стержень заклёпки может быть срезан по сечению аа. Силы  F  (рис.
б) передаются путём давления стенок отверстия на стержень заклепки.

Чтобы найти напряжения,  возникающие
в сечении  аа  стержня заклёпки под действием сил F ,
применяется метод сечений. Рассечем мысленно стержень заклёпки на две части и
рассмотрим условие равновесия одной из частей стержня (рис. б).

Со стороны листа на неё
передаётся внешняя сила F,
а по сечению аа действуют внутренние силы.
Поперечная сила Q,
возникающая в сечении аа уравновешивает внешнюю силу F
и численно равна ей Q=
F.

Приблизительно можно
принять, что касательные напряжения распределяются по сечению равномерно

                                                 t = Q/ А_ср.

Условие прочности
элементов работающих на срез, имеет вид

                                    
t = Q/ А_ср = £ [t_ср],                           где

А_ср –
площадь среза,

Q
– поперечная сила возникающая в сечении,

[t_ср]
– допускаемое касательное напряжение.

Величину допускаемого
напряжения  назначают на основании испытаний на срез. Обычно принимают    [t_ср] = (0,7 – 0,8) [d].     

На стержень заклепки
давление со стороны отверстия в листе передается по боковой поверхности
полуцилиндра высотой, равной толщине листа d  
(рис.1а и 1б).

Напряжения смятия
распределены по поверхности неравномерно. Так как закон их распределения точно
неизвестен, расчет ведут упрощенно, считая их постоянными по расчетной площади
смятия.

Проверку элементов
конструкции на смятие проводят по формуле

                                            d_см
= Q/ А_см £ [d_см
],                     
 где

А_см
– площадь смятия,

[d_см
] – допускаемое напряжение на смятие.  Обычно
принимают  [d_см ]
= (1,7-2,2)  [d_см ]
. Расчетные площади среза и смятия (  А_ср и А_см) вычисляются
в каждом конкретном случае в зависимости от вида соединения и характера
передаваемого усилия. Так, для заклепочного соединения  на рис.1а   и 
1б площадь среза одной заклепки соответствует её поперечному сечению   А_ср
= pd²/4.
За площадь смятия заклепки условно принимается её диаметральное сечение под
одним листом, то есть прямоугольник  (рис. 1б и1в)  Асм
= dd.

Пример.

Определить, исходя из условий прочности на срез и смятие,
необходимый диаметр болта в соединении, показанном на рис. 2, если d = 20 мм; d₁ = 12 мм; допускаемые
напряжения: [t_ср] = 100 Н/мм²; [d_см] = 240 Н/мм²;
растягивающая сила F =
120кН. Болт установлен в отверстие без зазора.

Р е ш е н и е.

Так как болт работает на
срез одновременно по двум сечениям – аа  и  bb,
то общая площадь среза составит

А_ср
= 2pd²/4
= pd²/2.

Поперечная сила в болте
равна силе, растягивающей стык Q
= F.

По условию прочности на
срез имеем

А_ср
= pd²/2
³  F[t_ср],

Откуда получаем

d ³
 F/p[t_ср]
= 2120 10³/3,14 100 = 27,6 мм.

Согласно данным задачи  2d₁,   поэтому
опасной в отношении смятия является площадь смятия внутренней детали  Асм = d.

Из условия прочности на
смятие

Асм
=F/
[d_см ],             
или

d ³
F/
[d_см ], 
           отсюда

d  ³
F/
d[d_см
]  =  120   10³ / 20
 240 = 25 мм.

Из двух значений
диаметра  d,
найденных по условиям прочности на срез и смятие, следует принять большее, то
есть  d 
³

З а д а н и е.

Определить, исходя из
условий прочности на срез и смятие, необходимый диаметр болта в соединении,
показанном на  рис. а,  если d = 35 мм;
допускаемые напряжения: [t_ср]
= 120 Н/мм²; [d_см]
= 280 Н/мм²; растягивающая сила F
= 220кН. Болт установлен в отверстие без зазора.

Сдвигом
называется такой вид деформации, при
которой в любом поперечном сечении
бруса возникает только попереч­ная
сила.
Деформацию сдвига можно наблюдать,
например, при резке ножницами металлических
полос или прутков (рис. 20.1, а).

Рассмотрим
брус площадью поперечного сечения А,
перпен­дикулярно оси которого
приложены две равные и противопо­ложно
направленные силы F;
линии действия их параллельны и

находятся
на относительно не­большом расстоянии
друг от друга. Для определения попе­речной
силы Q
применим ме­тод сечений (рис, 20.1, б).

FV

а б

Рис.
20.1

Во
всех точках поперечного сечения
действуют распреде­ленные силы,
равнодействую­щую которых определим
из ус­ловия равновесия оставленной
части бруса;

откуда
определим поперечную силу

Q=F-

Поперечная
сила есть равнодействующая внутренних
касатель­ных сил в поперечном сечении
при сдвиге.

Естественно
считать, что при сдвиге в поперечном
сечении бруса действуют только
касательные напряжения т. Предполага­ем,
что эти напряжения распределены по
сечению равномерно и, следовательно,
их можно определить по формуле

1. =
   Q/A.

Очевидно,
что при сдвиге форма сечения на значение
напряже­ния не влияет.

Примечание.
Изложенный в этом подразделе расчет
касательных напряжений при сдвиге
приближенный, так как линии действия
сил F
и Q
(см.
рис. 20.1, б)
не направлены по одной прямой и, строго
говоря, эти си­лы не являются
уравновешенной системой, а представляют
собой пару сил. Однако момент этой пары
(ввиду малого плеча) невелик, и
соответст­вующими ей напряжениями
можно пренебречь.

1. Расчеты
   на прочность при сдвиге

Условие
прочности детали конструкции заключается
в том, что наибольшее напряжение,
возникающее в ней (рабочее напряже­ние),
не должно превышать допускаемое.

Расчетная
формула при сдвиге

t
= Q/A<[x]

читается
следующим образом: касательное
напряжение при сдвиге,
вычисленное по формуле %
= Q/А,
не должно превышать допускае­мое.

По
этой расчетной формуле проводят проектный
и провероч­ный расчеты и определяют
допускаемую нагрузку.

Деформация
сдвига, доведенная до разрушения
материала, на­зывается срезом
(применительно к металлическим деталям)
или скалыванием
(применительно к неметаллическим
конст­рукциям).

Допускаемое
напряжение на срез выбирают для пластичных
ма­териалов в зависимости от предела
текучести. В машиностроении для штифтов,
болтов, шпонок и т.п. принимают

[т_ср]
= (0,25…0,35)а_т.

Для
древесины допускаемые напряжения на
скалывание во вруб­ках колеблются в
пределах от 0,5 до 1,4 МПа и зависят от
сорта дере­ва и направления врубки
по отношению к направлению волокон.

При
расчетах на срез в случае, если соединение
осуществляется несколькими одинаковыми
деталями (болтами, заклепками и т.д),
полагают, что все они нагружены
одинаково.

Расчеты
соединений на срез обычно сопровождают
проверкой прочности этихЪэединений на
смятие.

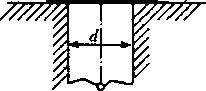
Пример
20.1. Определить силу F,
необходимую для пробивания квад­ратного
отверстия размером а
= 25 мм в стальной полосе толщиной 5 = = 10
мм, если предел прочности при срезе т_в
– 360 МПа. Определить на­пряжения сжатия
в пуансоне (рис. 20.2).

Решение.
Определим разрушающую нагрузку F:

Площадь
среза А_ср
равна площади боковой поверхности
пробитого от­верстия:

а

Д_р
= = 4 * 25 * КГ³
•
10 • Ю’³
= 1000 10″* м².
Следовательно, F
— т_вД._р
= 360-10⁶
-1000 10^-6
= 360 10³
Н.

D

F

Определим
напряжения сжатия в пуансоне:

о_с=F/A,

где
А
—
площадь поперечного сечения пуансона;

Л
= л²
=
25²-10-⁶
= 625-10-⁶
м²,

следовательно,

<у_с
= F/A
=
360-10³/
(625 ■ 10^-6)
= 576 1 0⁶
Па = 576 МПа.

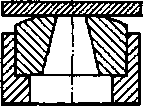
Пример
20.2. Определить напряжения смятия и среза
в головке стержня, растягиваемого силой
F=
100 кН. Дано: D
=
32 мм, d=
20 мм, h
= = 12 мм (рис. 20.3).

Решение.
Определим площадь смятия Л_СЧ1
и площадь среза А_ср
го­ловки. Площадь опорной поверхности
головки, работающей на смятие, равна

Д_м
= nD²/4
– пd²
/4 = –
d*)/4
= 3,14(32²
– 20²)
• 10″⁶
/4 = 490 • 10~⁶
м².

Площадь
среза равна площади боковой поверхности
цилиндра диа­метром d
и высотой h

А_ср
= ndh
= 3,14- 20-10^_3
■ 12 • 10~³
= 754-10“⁶
м².

Определим
напряжения смятия и среза головки:

а_см
= F/A_CM
= 100*10³/(490*10″⁶)
= 204 10⁶
Па = 204 МПа; о_ср
= F/A^
= 100 10³/
(754 * tO^-6)
= 133-10⁶
Па = 103 МПа.

Пример
20.3. В условиях примера 19.6 определить
напряжения среза в болте (см. рис. 19.14).

Решение.
Напряжения среза в болте определяем по
формуле т = F/Др.
Площадь среза Л_ср
представляет собой две площади
попереч­ного сечения болта:

Аср
= 2nd²/4
= nd²/2,

следовательно,

т_ср
= F/A_c?
= 2F/(nd²)
= 2 • 32 ■ 10³
/ (ЗД 4 • 400 • 10^-6)
= 54-10⁶
Па = 54 МПа.

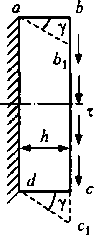
1. Деформация
   и закон Гука при сдвиге

Для
установления параметров, характеризующих
деформацию при сдвиге, рассмотрим
элемент бруса в виде параллелепипеда
abed,
на грани которого дейст­вуют только
касательные напряжения х, а противопо­ложную
грань параллелепипеда представим жестко
за­щемленной (рис. 20.4). Деформация
сдвига в указан­ном элементе заключается
в перекашивании прямых углов параллелепипеда
за счет поступательного пере­мещения
грани Ьс
по отношению к сечению, принято* му за
неподвижное. Деформация сдвига
характеризу­ется углом у и называется
углом
сдвига,
или о т – Рис.20.4 носительным
сдвигом
(так как этот параметр

не
зависит от расстояния h,
на котором происходит сдвиг). Величи­на
bb_v
на которую смещается подвижная грань
относительно не­подвижной, называется
абсолютным
сдвигом.
Относитель­ный сдвиг у выражается в
радианах.

Напряжения
и деформации при сдвиге связаны между
собой за­висимостью, которая называется
законом
Гука при сдвиге.

Закон
Гука при сдвиге справедлив лишь в
определенных преде­лах нагружения и
формулируется так: касательное
напряжение прямо пропорционально
относительному сдвигу.

Математически
закон Гука можно записать в виде равенства

т
= Gy.

Коэффициент
пропорциональности G
характеризует жест­кость материала
(т.е. способность сопротивляться упругим
де­формациям) при сдвиге и называется
модулем
сдвига или модулем упругости второго
рода.

Модуль
упругости и напряжение выражаются в
одинаковых единицах:

[G]
= [т]/[у] = Па.

Приведем
значения G,
МПа, для некоторых материалов:

Чугун 4,5Ю⁴

Сталь 8,1-Ю⁴

Медь (4,0…
4,9)-10⁴

Латунь (3,5…
3,7)-10⁴

Алюминий (2,6…
2,7V
10⁴

Дерево 0,055-10

В
заключение отметим, что между тремя
упругими постоянны­ми Е,
G
и v
существует следующая зависимость:

G
= E/[2(1+v)].

Принимая
для сталей v
= 0,25, получаем

G_CT
~0,4£_ст.

1. Закон
   парности касательных напряжений

Закон
парности касательных напряжений
фор­мулируется так: касательные
напряжения в двух взаимно-перпен-
дикулярных площадках,
перпендикулярные
их общему ребру, равны по модулю.

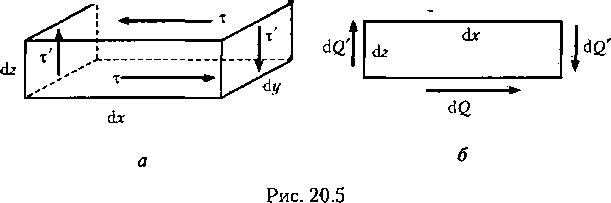
Внутри
тела вблизи некоторой точки вырежем
элементарный параллелепипед с размерами
dr,
dу,
dz
(рис. 20.5, а).

Пусть
на верхней грани этого параллелепипеда
действует каса­тельное напряжение
т. Сила, действующая в этой грани, равна

dQ
=
%<bcdy.

Так
как параллелепипед находится внутри
тела в равновесии, то – О, следовательно,
на нижней грани параллелепипеда будет

действовать
такая же сила dQ,
но направленная в противополож­ную
сторону. Пара сил (dQ,
dQ)
будет стремиться вращать парал­лелепипед
против часовой стрелки (рис. 20.5, б).

Так
как параллелепипед находится в равновесии,
то = 0,

следовательно,
пара сил (dQ,
dQ)
будет уравновешиваться ка­кой-то
другой парой с моментом, равным моменту
первой пары. Естественно считать, что
вторая пара образуется касательными
на­пряжениями т’, действующими на
боковых (правой и левой) гра­нях
параллелепипеда, причем dQ’
= %’dydz.
Следовательно,

M(dQ,dQ)
= M(dQ’,dQ’)

или

xdxdydz
—
t
‘dxdydz,

откуда

x-x

Обратим
внимание на то, что парные
касательные напряжения в двух
взаимно-перпендикулярных сечениях
направлены либо к линии пересечения
плоскостей сечений,
либо
от этой линии.

1. Напряжения
   в наклонных сечениях при растяжении.

Главные
напряжения

Через
всякую точку деформированного тела
можно провести бесчисленное множество
различно ориентированных секущих
плоскостей.

Рассмотрим
прямой брус постоянного поперечного
сечения А,
растягиваемый
силами F
(рис. 20.6, а).
Рассечем брус плоскостью 1—1,
проходящей через точку В
и составляющей с поперечным се­чением
угол <р, отбросим верхнюю часть и
рассмотрим равновесие нижней.

Очевидно,
что равнодействую­щая N
внутренних сил, действую­щих в наклонном
сечении, будет равна растягивающей силе
F:

Рис.
20.6

N
= F,

а
напряжения р_ф
будут параллель­ны оси бруса (рис.
20.6,6).
Полагая, что напряжения p_v
распределены по наклонному сечению
равномер­но, получим

p₉
= N/A_r

где
Л_ф
— площадь наклонного сече­ния.

Нормальные
напряжения о в поперечном сечении будут
равны

с
= М/
А

А

Так
как Л_ф
= A/cos<p,Top₉
– N/А_щ
=N/{А/cos<p)=
acos<p.

Разложим
полное напряжение р
в точке наклонного сечения на нормальное
с_ф
и касательное т_ф
напряжения (рис. 20.6, в); тогда

=
р_ф
costp
= acos²
ф;

=
ру
sincp
= стсоэф этф – (о/2.)5т2ф.

Отсюда
следует вывод: при
растяжении бруса в наклонных сече­ниях
возникают равномерно распределенные
по сечению нормаль­ные и касательные
напряжения и соответствующие этим
напря­жениям деформации растяжения
и сдвига.

Рассмотрим
частные случаи:

1. Ф
   = 0; а_ф
   = acos²
   ф = с = о_тах.

Нормальные
напряжения имеют максимальное значение
в по­перечном сечении:

=
(а/2)зт2ф =0.

Касательные
напряжения в поперечном сечении равны
нулю;

1. ф
   = 45°; с _ф
   = о cos²
   ф = а/2;
   т_ф
   = (ст/2) зт2ф = а/2 = т _тах.

Касательные
напряжения достигают своего максимального
зна­чения в сечениях, наклоненных к
оси под углом 45°. Эти напряже­ния
являются причиной появления на
растягиваемом образце при достижении
предела текучести сетки наклонных линий
Людер- са—Чернова;

1. ф
   = 90; ст_ф
   =0; т_ф=0.

f«.

ТГ”

Oi

<*2

“1

Линейное

Плоское

Рис.
20.7

В
продольных сечениях бруса нет ни
касательных, ни нормаль­ных напряжений
(вспомним гипотезу о ненадавливании
волокон).

Из
изложенного следует, что, говоря о
напряжении в данной точке, всегда
необходимо указать положение секущей
плоскости, в которой это напряжение
возникает.

Совокупность
нормальных и касательных напряжений,
возни­кающих в бесчисленном множестве
различно ориентированных площадок,
проходящих через данную точку,
характеризует напря­женное
состояние в данной точке.

Площадки,
в которые касательные
напряжения равны нулю,
на­зываются главными
площадками,
а возникающие в них нормальные напряжения
— главными
напряжениями.
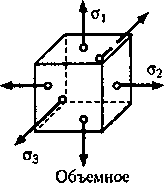
Как доказывается в теории упругости,
в общем случае напряженного состояния
в зоне исследуемой точки могут
существовать три вза­имно-перпендикулярные
главные площадки. «

В
зависимости от числа таких площадок
(где а * 0) различа­ют три основных вида
напряженного состояния: линейное
(одноосное),
плоское
(двухосное) и объемное
(трехосное) (рис. 20.7).

В
дальнейшем нас будут интересовать
только первые два вида напряженного
состояния.

Очевидно,
что в рассмотренном случае одноосного
растяжения главные площадки расположены
в поперечном и продольном сече­ниях,
т.е. взаимно-перпендикулярны. Обратим
внимание также на

то,
что главные
напряжения
в дан­ной точке имеют
максимальное и минимальное значения’.

=
e;
c_mi„
=о.

В
дальнейшем нам понадобит­ся зависимость
между не равными нулю главными
напряжениями в двух взаимно-перпендикулярных
площадках (случай плоского на­пряженного
состояния) и макси-

мальными
касательными напряжениями в наклонной
(по отноше­нию к главным) площадке.

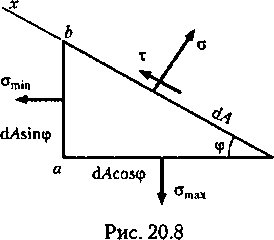
Для
вывода указанной зависимости внутри
бруса вблизи неко­торой точки вырежем
бесконечно малую призму abc
(рис. 20.8),
у которой ab
и ас
—
главные площадки, а <т_тах
и a_min
— главные на­пряжения. Площадь грани
Ьс
обозначим dA

Рассмотрим
равновесие призмы, для чего спроецируем
дейст­вующие на ее гранях силы на ось
х:

X
= 0;
TcL4 + a_min<L4sin<pcos((>-
a_maxcL4cos<p
sincp = 0,

откуда

‘^t= [(c^fm»-o_ni„)/2]sm29.

Из
этого уравнения следует, что при <р =
45°

^
^—^max(^max” ®tnin)

Еслиa_min
= 0_ктот_тах
= а_тах
/2.

Если
в случае плоского напряженного состояния
в окрестно­сти данной точки можно
выделить элементарный параллелепипед
таким образом, чтобы на его гранях
действовали только равные между собой
касательные напряжения (см. рис. 20.5, а),
то такой вид напряженного состояния
называется чистым
сдвигом. В
дальнейшем с чистым сдвигом мы встретимся
при изучении теории кручения круглого
цилиндра.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #