К решению задачи
рекомендуется приступить после решения
самостоятельной работы 7.
1.
Задаются
величиной коэффициента продольного
изгиба ф.
В первом приближении его можно принять
равным 0,6…0,8.
2.
Определяют
требуемую площадь поперечного сечения
стойки
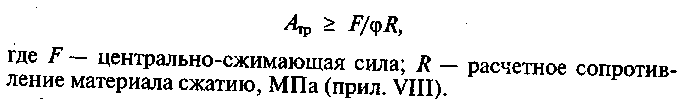
3. По
найденной площади определяют номера
профилей проката, из
которых состоит сечение, используя
прил. I.
В рамках расчетной работы рекомендуется
принять профили одинаковыми по площади,
если их несколько.
В практических
расчетах приходится решать различные
задачи: обеспечить равную в обеих
плоскостях устойчивость стойки или
наперед заданное отношение жесткостей
(устойчивостей) и т.д. Сложной задачей
является выбор типа сечения, его
габаритов, которая довольно сложна
и требует специальных знаний, поэтому
рекомендации по подбору сечения упрощены.
4.
Проверяют
устойчивость принятого сечения в
следующем порядке:
а) определяют
расчетную длину стержня:
148
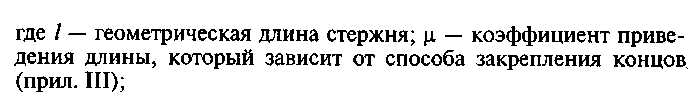
б)
определяют моменты инерции сечения Jx
и
Jy
относительно
главных центральных осей х
и
у,
которые
совпадают с осями симметрии сечения.
Моменты инерции профилей проката
относительно собственных осей
определяются по ГОСТам (прил. I);
в)
определяют радиусы инерции сечения
относительно осей х
и
у.
г)
определяют гибкость стержня относительно
осей х
и
у:
д) по
наибольшему значению Л и в зависимости
от материала стойки определяют коэффициент
продольного изгиба ф (прил. IV);
е) подставляют полученные значения в
формулу:
Если это условие
удовлетворено, то устойчивость стержня
обеспечена, если не удовлетворено — не
обеспечена. Если несущая способность
стойки не обеспечена, то необходимо
увеличить площадь сечения, приняв
больший профиль, и проверить устойчивость
стойки, добиваясь того, чтобы напряжение
было меньше расчетного сопротивления.
Если напряжение в стойке равно расчетному
сопротивлению или немного меньше, то
сечение считается рационально
подобранным, т. е. экономичным. Если
напряжение намного меньше расчетного
сопротивления, то такое сечение не
экономично, так как имеет большой запас
прочности. Поэтому, если недонапряжение
составляет более 5 %, то следует уменьшить
площадь сечения (или увеличить гибкость)
стойки, добиваясь, чтобы недонапряжение
не превышало 5 %. В некоторых случаях
этого не удается добиться из-за
ограниченности сортамента профилей
проката.
Пример
32.
Подобрать сечение центрально-сжатой
составной стойки, показанной на рис.
47. Материал стойки — сталь С-245.
Решение.
1.
Задаемся
величиной ф
= 0,7.
2.
Определим
требуемую площадь сечения
149

где
R
– 240
МПа — расчетное сопротивление
стали С-24 (прил. VIII).
Принимаем
все профили одинаковыми по площади. На
один профиль требуется площадь 50,6 : 3 =
16,8 см2.
Принимаем два швеллера № 14а площадью
А1
= 1 • 17
= 34 см2
и двутавровую балку № 14 площадью А2
=
17,4 см2.
Общая площадь сечения
А =
34 +17,4 = 51,4 см2
(см.
табл. 3 и 4 прил. I).
3.
Проверим
устойчивость принятого сечения стержня
в
следующем порядке:
а) определим
расчетную длину стержня
где
-ц = 1 для стержня с шарнирным закреплением
концов (прил. III);
б)
определим момент инерции сечения
относительно оси х:
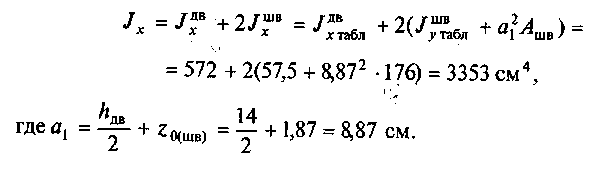
150
Определим
момент инерции сечения относительно
оси у:
в) определим радиусы
инерции сечения
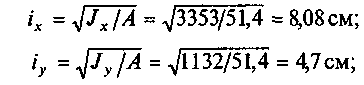
г)
определим гибкость стержня относительно
осей х
и
у:
д) для
наибольшего значения гибкости Ху
= 85,1
определим коэффициент ф (см. прил.
IV)
по
интерполяции между значениями
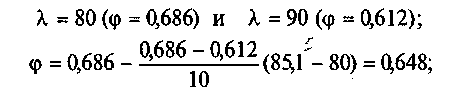
е) определим
расчетное напряжение в сечении
Это недопустимо,
поэтому необходим перерасчет.
1. Принимаем во
втором приближении среднее значение
между тем, которым задались, и тем,
что получили:
2. Требуемая площадь
сечения
На
один профиль требуется 51,6 : 3 = 17,2 см2.
Принимаем два швеллера № 16 с А{
= 2
• 18,1 = 36,2 см2
и двутавровую балку № 14 с А2
=
17,4 см2.
Полная площадь сечения
А =
2-18,1
+ 17,4 + 53,6 см2.
3. Проверим
устойчивость стойки:
а) /о = 4 м, осталось
прежним;
б)
поскольку Jx
> Jy,
определим
наименьший момент инерции, который дает
наибольшую гибкость:
151
в) радиус инерции
г) гибкость стержня
д) коэффициент
продольного изгиба получим интерполяцией
между
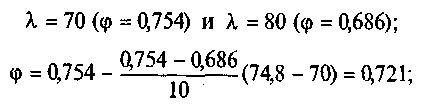
е) расчетное
напряжение
ж) недонапряжение
равно
что допустимо, но
нежелательно.
Выполним перерасчет,
уменьшив номера профилей и, как правило,
площадь поперечного сечения.
Возможны
такие варианты сечения: двутавровая
балка № 16 и два швеллера № 14 (А
= 51,4
см2);
двутавровая балка № 16 и два швеллера №
14 а (А
=
54,2 см2).
В первом случае напряжение а = = 268,4 МПа,
во втором о =243,5 МПа. Решение необходимо
провести самостоятельно по приведенной
ранее схеме. В обоих случаях напряжения
получились больше расчетного сопротивления
R
= 240
МПа, что недопустимо.
Нам
не удалось добиться того, чтобы
недонапряжение стало меньше 5 %, поэтому
оставляем сечение из двутавровой балки
№ 14 и двух швеллеров № 16 (А
= 53,6
см2
и R
=
219,9 МПа).
Интересно
отметить, что при площади сечения А
= 53,6
см2
стойка
недонапряжена на 8,37 %, а при площади
сечения А
= = 54,2
см2
перенапряжена на 1,4 %, т.е. при меньшей
площади стойка обладает большей
устойчивостью (жесткостью). Такое явление
происходит потому, что кроме площади
сечения на устойчивость стойки влияют
другие геометрические характеристики.
Ответ:
принято
сечение стойки из двух швеллеров № 16 и
двутавровой балки № 14.
152
Задание
для расчетно-графической работы 7.
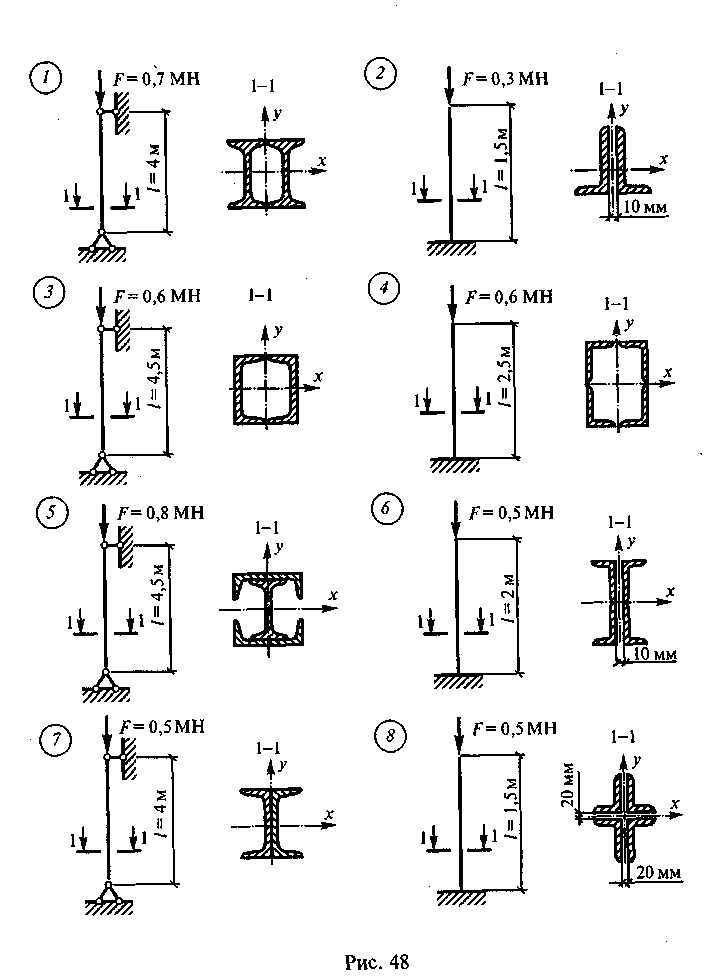
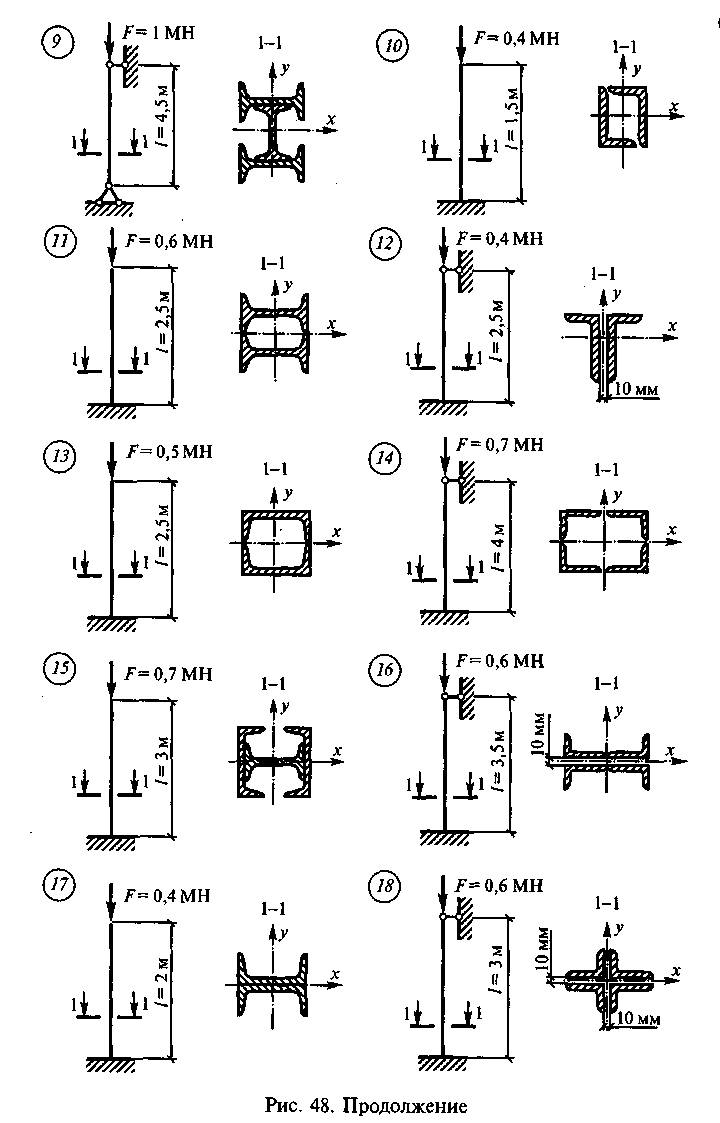
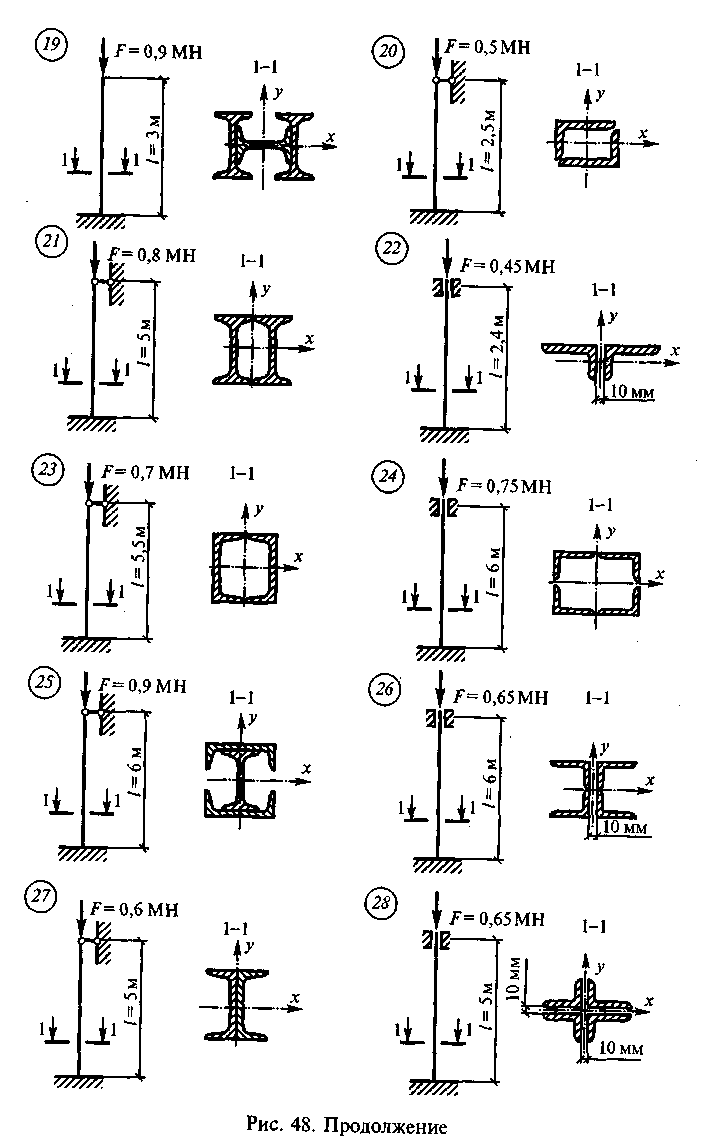
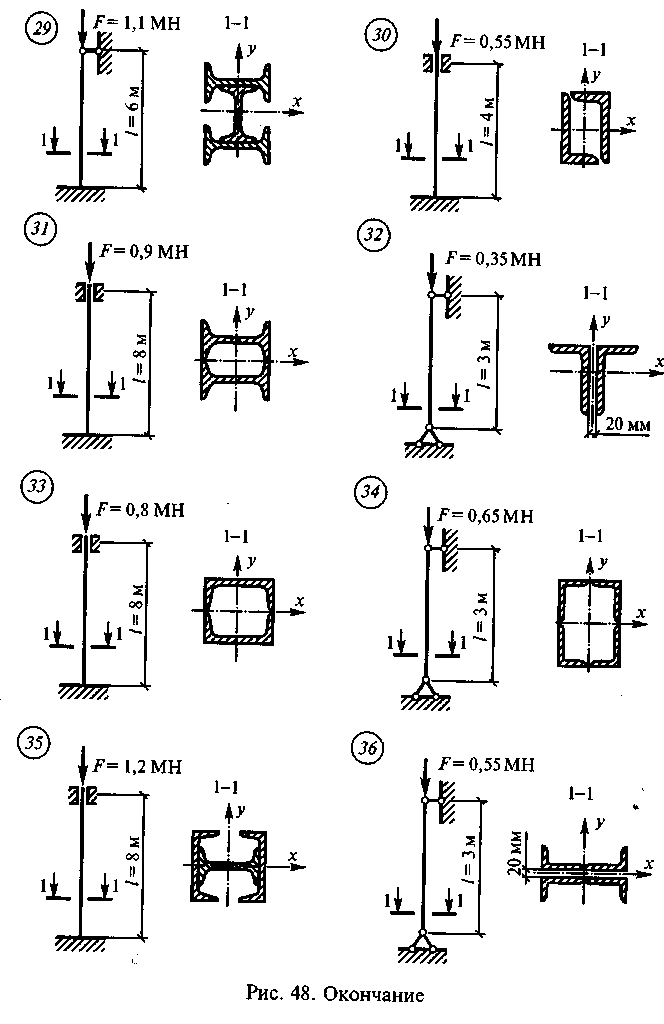
Подобрать сечение центрально-сжатой
стойки по данным одного из вариантов,
показанных на рис. 48. Материал стойки
для нечетных вариантов — сталь С-245, для
четных вариантов — сталь С-345.
153
154
155
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Расчет площади прямоугольника
|
a= |
|
|
b= |
Рассчитать
Расчет площади треугольника
Способ нахождения площади треугольника:
|
a= |
|
|
b= |
|
|
c= |
Рассчитать
Расчет площади параллелограмма
Способ нахождения площади параллелограмма:
|
a= |
|
|
h= |
|
Рассчитать
Расчет площади правильного многоугольника
|
n= |
|
|
a= |
Рассчитать
Расчет площади круга
Рассчитать площадь круга, если известен:
радиус круга – r
диаметр круга – d
|
r= |
|
Рассчитать
Расчет площади эллипса
|
a= |
|
|
b= |
Рассчитать
Расчет площади сектора круга
Рассчитать площадь сектора круга, если известен:
угол сектора – θ
длина дуги – L
|
r= |
|
|
θ= |
Рассчитать
Расчет площади трапеции
Способ нахождения площади трапеции:
|
a= |
|
|
b= |
|
|
h= |
|
|
Рассчитать |
Калькулятор для расчета площади
Данный онлайн-калькулятор позволяет рассчитать площадь различных геометрических фигур, таких как:
|
|
Для удобства расчетов вы можете выбрать единицу измерения (миллиметр, сантиметр, метр, километр, фут, ярд, дюйм, миля). Также полученный результат можно конвертировать в другую единицу измерения путем выбора её из выпадающего списка.
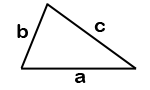
Способ нахождения площади треугольника:
| a= |
|
| b= | |
|
c= |
Вычислить
Рассчитать площадь круга, если известен:
| r= |

|
Вычислить
Способ нахождения площади параллелограмма:
| a= |

|
| h= | |
Вычислить
Рассчитать площадь сектора круга, если известен:
|
r= |

|
|
θ= |
Вычислить
Способ нахождения площади трапеции:
Площадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры.
| Метрические единицы измерения площади: | |
| Квадратный метр, производная единица системы СИ 1 м2 = | 1 са (сантиар) |
| Квадратный километр – 1 км2 = | 1 000 000 м2 |
| Гектар – 1 га = | 10 000 м2 |
| Ар (сотка) – 1 а = | 100 м2 (сотка как правило применяется для измерения земельных участков и равна 100 м2 или 10м х 10м) |
| Квадратный дециметр, 100 дм2 = | 1 м2; |
| Квадратный сантиметр, 10 000 см2 = | 1 м2; |
| Квадратный миллиметр, 1 000 000 мм2 = | 1 м2. |
Данный онлайн-калькулятор удобен при расчете площадей помещений и земельных участков.
Общая площадь поверхности квадратного столба Калькулятор
| Search | ||
| Дом | математика ↺ | |
| математика | Геометрия ↺ | |
| Геометрия | 3D геометрия ↺ | |
| 3D геометрия | Квадратный столб ↺ | |
| Квадратный столб | Площадь поверхности квадратного столба ↺ | |
| Площадь поверхности квадратного столба | Общая площадь поверхности квадратного столба ↺ |
|
✖Базовые кромки квадратной колонны — это стороны одинаковой длины, которые соединяются, образуя квадратную колонну.ⓘ Базовые края квадратной колонны [BEdges] |
+10% -10% |
||
|
✖Высота квадратного столба — это расстояние между самой низкой и самой высокой точками квадратного столба.ⓘ Высота квадратного столба [h] |
+10% -10% |
|
✖Общая площадь поверхности квадратного столба — это общая площадь двухмерного пространства, занимаемого всеми гранями квадратного столба.ⓘ Общая площадь поверхности квадратного столба [TSA] |
⎘ копия |
Общая площадь поверхности квадратного столба Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Базовые края квадратной колонны: 10 метр –> 10 метр Конверсия не требуется
Высота квадратного столба: 12 метр –> 12 метр Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
680 Квадратный метр –> Конверсия не требуется
5 Общая площадь поверхности квадратного столба Калькуляторы
Общая площадь поверхности квадратного столба формула
Общая площадь поверхности квадратного столба = 2*((Базовые края квадратной колонны^2)+(2*Базовые края квадратной колонны*Высота квадратного столба))
TSA = 2*((BEdges^2)+(2*BEdges*h))
Что такое квадратный столб?
Столб представляет собой большую, обычно цилиндрическую или квадратную, прочную конструкцию, которая стоит вертикально в качестве опоры дома или здания как конструктивно, так и эстетически. Прямоугольный кубический столб с двумя ребрами одинаковой длины является квадратным столбом. Различные типы квадратных столбов: романские, рифленые, конические и кирпичные.
У всех у нас часто возникает необходимость узнать площадь помещения, а сделать это можно или рассчитать самостоятельно или использовать для вычислений онлайн калькулятор.
Калькулятор площади помещения
Площадь комнаты необходимо знать например, для подбора необходимого количества материала для потолка или напольного покрытия. В более сложных калькуляторах есть еще и подсчет периметра и площади стен.
Разберём подробнее эту тему…
Расчет площади помещения по формуле
Расчет площади помещения делается очень просто. Площадь жилого помещения считается так же как и площадь любой прямоугольной фигуры или квадрата. Нужно всего то ширину помещения умножить на длину помещения. Это математика 3-го класса.
Формула для расчета площади помещения:
S = B * L , где
B — ширина помещения,
L — длина помещения.
Давайте рассмотрим небольшой пример. Допустим у нас есть помещение с размерами 3 на 4 метра. Подставим эти значения в нашу формулу и найдем общую площадь помещения в метрах квадратных.
S = 3 * 4 = 12 м2.
Так фактически мы рассчитали площадь пола или площадь потолка. Для простого прямоугольного помещения они будут равны.
Калькулятор площади помещения
Чтобы выполнить расчет площади помещения используя наш онлайн калькулятор достаточно выполнить всего несколько действий. В соответствующие поля введите сперва ширину помещения, а затем его длину. Не забудьте выбрать единицы измерения (метры, сантиметры или миллиметры).
Когда вы ввели все исходные данные нажмите на кнопку расчет и сразу же получите результаты расчета. Итоговая площадь может быть в выбранных вами единицах измерения (м2, см2 или мм2). Точность калькулятора площади составляет два знака после запятой.
Вот так легко и быстро рассчитает площадь помещения наш калькулятор. К тому же он бесплатный и простой, так что можете пользоваться.
В строительстве бывает так что ещё необходимо знать и площадь всех стен комнаты. Для этого есть калькулятор стен онлайн.
Было полезно? Поделитесь с друзьями!