Площадь стороны куба является площадью квадрата и представляет собой сторону квадрата, возведенную во вторую степень. Так как сторона любого квадрата-грани в кубе – это ребро куба, следовательно, ребро куба, выраженное через площадь стороны, приобретает вид квадратного корня из площади.
a=√S
Если необходимо рассчитать площадь боковой или полной поверхности куба, то это можно сделать, не проводя расчетов по вычислению ребра. Площадь боковой поверхности куба представлена четырьмя боковыми гранями, площадь которых уже известна, а площадь полной поверхности – всеми шестью гранями куба.
S_(б.п.)=4S
S_(п.п.)=6S
Для расчета всех последующих параметров понадобится полученная формула для ребра куба через площадь грани. Объем куба вычисляется как возведение ребра в третью степень, следовательно, объем куба через площадь грани равен квадратному корню из площади в третьей степени.
V=a^3=√(S^3 )
Чтобы вычислить периметр куба, нужно умножить его ребро на двенадцать, то есть умножить на двенадцать квадратный корень площади стороны куба..
P=12a=12√S
Диагональ стороны куба через теорему Пифагора выражается, как сторона квадрата или ребро куба, умноженное на корень из двух. Таким образом, диагональ стороны куба через площадь имеет вид квадратного корня из удвоенной площади.
d=a√2=√2S
Чтобы вычислить диагональ куба, нужно провести диагональ в его основании, тогда они в совокупности с боковым ребром образуют прямоугольный треугольник, в котором диагональ куба будет равна ребру, умноженному на корень из тех. Так как ребро должно быть выражено через площадь грани, диагональ куба равна квадратному корню из утроенной площади. (рис.2.1)
a^2+d^2=D^2
D^2=a^2+2a^2
D^2=3a^2
D=a√3=√3S
Сфера, вписанная в куб, обладает диаметром, равном по значению ребру куба, значит радиус такой сферы будет равен половине ребра или половине квадратного корня из площади стороны куба. (рис. 2.2)
r=a/2=√S/2
Чтобы вычислить радиус сферы, описанной вокруг куба, необходимо разделить пополам его диагональ. Так как диагональ куба равна квадратному корню из утроенной площади стороны куба, то радиус описанной сферы будет его половиной. (рис.2.3)
R=D/2=√3S/2
Как найти сторону куба зная площадь поверхности. Как найти площадь куба
Площадь поверхности куба.
Площадь поверхности куба – это суммарная площадь всех поверхностей фигуры. Площадь поверхности куба равна сумме площадей всех его шести граней. Площадь поверхности является числовой характеристикой поверхности. Для вычисления площади поверхности куба, Вам необходимо знать определенную формулу и длину одной из сторон куба. Для того чтобы Вы могли оперативно вычислить площадь поверхности куба, вам необходимо запомнить формулу и сам порядок действий. Чуть ниже мы подробно разберем порядок вычисления полной площади поверхности куба и приведем конкретные примеры.

Определение площади поверхности куба.
Определение площади поверхности куба выполняется по формуле SA = 6а 2 . Куб (правильный гексаэдр) – это один из 5 видов правильных многогранников, который является правильным прямоугольным параллелепипедом, куб имеет 6 граней, каждая из этих граней является квадратом.

Для вычисления площади поверхности куба Вам необходимо записать формулу SA = 6а 2 . Теперь давайте разберем почему данная формула имеет такой вид. Как мы говорили ранее, куб имеет шесть равных квадратных граней. Исходя из того что стороны квадрата равны, площадь квадрата составлять – a 2 , где а – сторона куба. Так куба имеет 6 равных квадратных граней, то для определения площади его поверхности, Вам необходимо умножить площадь одной грани (квадрата) на шесть. В итоге получаем формулу для вычисления площади поверхности (SA) куба: SA = 6а 2 , где а – ребро куба (сторона квадрата).
Чему равна площадь поверхности куба.
Площадь поверхности куба измеряется в квадратных единицах, к примеру, в мм 2 , см 2 , м 2 и так далее. Для дальнейших расчетов Вам необходимо будет измерить ребро куба. Как мы знаем, ребра у куба равны, поэтому Вам будет достаточно измерить только одно (любое) ребро куба. Выполнить такой замер Вы можете при помощи линейки (или рулетки). Обратите внимание на единицы измерения на линейке или рулетке и запишите значение, обозначив его через а.

Полученное значение возведите в квадрат. Таким образом, Вы возведите в квадрат длину ребра куба. Для того чтобы возвести число в квадрат умножьте его на себя. Наша формула будет иметь следующий вид: SA = 6*а 2
Вы вычислили значение площади одной из граней куба.
a 2 = 2 х 2 = 4 см 2
Полученное значение умножайте на шесть. Не забывайте, что у куба 6 равных граней. Определив площадь одной из граней, умножьте полученное значение на 6, чтобы все грани куба участвовали в расчете.
Вот мы и пришли к конечному действию по вычислению площади поверхности куба.
Как найти площадь поверхности куба?
Куб обладает множеством интересных математических свойств и известен людям с давних времен. Представители некоторых древнегреческих школ считали, что элементарные частицы (атомы), из которых состоит наш мир, имеют форму куба, а мистики и эзотерики даже обожествляли эту фигуру. И сегодня представители паранауки приписывают кубу удивительные энергетические свойства.
Куб – это идеальная фигура, одно из пяти Платоновых тел. Платоново тело – это

1. Все ее ребра и грани равны.
2. Углы между гранями равны (у куба углы между гранями равны и составляют 90 градусов).
3. Все вершины фигуры касаются поверхности описанной вокруг нее сферы.
Точное количество этих фигур назвал древнегреческий математик Теэтет Афинский, а ученик Платона Евклид в 13-ой книге Начал дал им подробное математическое описание.
Древние греки, склонные с помощью количественных величин описывать строение нашего мира, придавали Платоновым телам глубокий сакральный смысл. Они считали, что каждая из фигур символизирует вселенские начала: тетраэдр – огонь, куб – землю, октаэдр – воздух, икосаэдр – воду, додекаэдр – эфир. Сфера же, описанная вокруг них, символизировала совершенство, божественное начало.
Итак, куб, называемый также гексаэдром (от греч. “hex” – 6), – это трехмерная правильная геометрическая фигура. Его также называют правильной четырехугольной призмой или прямоугольным параллелепипедом.
У куба шесть граней, двенадцать ребер и восемь вершин. В эту фигуру можно вписать другие правильные многогранники: тетраэдр (четырехгранник с гранями в виде треугольников), октаэдр (восьмигранник) и икосаэдр (двадцатигранник).
Диагональю куба называется отрезок, соединяющий две симметричные относительно центра вершины. Зная длину ребра куба a, можно найти длину диагонали v: v = a 3.
В куб, как говорилось выше, можно вписать сферу, при этом радиус вписанной сферы (обозначим r) будет равен половине длины ребра: r =(1/2)а.
Если же сферу описать вокруг куба, то радиус описанной сферы (обозначим его R) будет равен: R= ( 3/2)a.
Довольно распространенный в школьных задачах вопрос: как вычислить площадь

Аналогично тому, как мы нашли площадь поверхности куба, рассчитаем площадь его боковых граней: Sб=4а 2.
Из этой формулы понятно, что две противолежащие грани куба – это основания, а остальные четыре – боковые поверхности.
Отыскать площадь поверхности куба можно и другим способом. Учитывая тот факт, что куб – это прямоугольный параллелепипед, можно воспользоваться понятием трех пространственных измерений. Это значит, что куб, являясь трехмерной фигурой, имеет 3 параметра: длину (а), ширину(b) и высоту (c).
Используя эти параметры, вычислим площадь полной поверхности куба: Sп= 2(ab+ас+bc).
Чтобы рассчитать площадь боковой поверхности куба, периметр основания необходимо умножить на высоту: Sб= 2c(a+b).
Объем куба – это произведение трех составляющих – высоты, длины и ширины:
V= abc либо трех смежных ребер: V=а 3.
Уравнение поверхности куба. Как найти площадь куба
Куб обладает множеством интересных математических свойств и известен людям с давних времен. Представители некоторых древнегреческих школ считали, что элементарные частицы (атомы), из которых состоит наш мир, имеют форму куба, а мистики и эзотерики даже обожествляли эту фигуру. И сегодня представители паранауки приписывают кубу удивительные энергетические свойства.
Куб – это идеальная фигура, одно из пяти Платоновых тел. Платоново тело – это
правильная многогранная фигура, удовлетворяющая трем условиям:
1. Все ее ребра и грани равны.
2. Углы между гранями равны (у куба углы между гранями равны и составляют 90 градусов).
3. Все вершины фигуры касаются поверхности описанной вокруг нее сферы.
Точное количество этих фигур назвал древнегреческий математик Теэтет Афинский, а ученик Платона Евклид в 13-ой книге Начал дал им подробное математическое описание.
Древние греки, склонные с помощью количественных величин описывать строение нашего мира, придавали Платоновым телам глубокий сакральный смысл. Они считали, что каждая из фигур символизирует вселенские начала: тетраэдр – огонь, куб – землю, октаэдр – воздух, икосаэдр – воду, додекаэдр – эфир. Сфера же, описанная вокруг них, символизировала совершенство, божественное начало.
Итак, куб, называемый также гексаэдром (от греч. “hex” – 6), – это трехмерная правильная Его также называют или прямоугольным параллелепипедом.

У куба шесть граней, двенадцать ребер и восемь вершин. В эту фигуру можно вписать другие тетраэдр (четырехгранник с гранями в виде треугольников), октаэдр (восьмигранник) и икосаэдр (двадцатигранник).
Называется отрезок, соединяющий две симметричные относительно центра вершины. Зная длину ребра куба a, можно найти длину диагонали v: v = a 3.
В куб, как говорилось выше, можно вписать сферу, при этом радиус вписанной сферы (обозначим r) будет равен половине длины ребра: r =(1/2)а.
Если же сферу описать вокруг куба, то радиус описанной сферы (обозначим его R) будет равен: R= (3/2)a.
Довольно распространенный в школьных задачах вопрос: как вычислить площадь

поверхности куба? Очень просто, достаточно наглядно представить себе куб. Поверхность куба состоит из шести граней в форме квадратов. Следовательно, для того, чтобы найти площадь поверхности куба, сначала нужно найти площадь одной из граней и умножить на их количество: S п = 6а 2.
Аналогично тому, как мы нашли площадь поверхности куба, рассчитаем площадь его боковых граней: S б =4а 2.
Из этой формулы понятно, что две противолежащие грани куба – это основания, а остальные четыре – боковые поверхности.
Отыскать куба можно и другим способом. Учитывая тот факт, что куб – это прямоугольный параллелепипед, можно воспользоваться понятием трех пространственных измерений. Это значит, что куб, являясь трехмерной фигурой, имеет 3 параметра: длину (а), ширину(b) и высоту (c).
Используя эти параметры, вычислим площадь полной поверхности куба: S п = 2(ab+ас+bc).
Объем куба – это произведение трех составляющих – высоты, длины и ширины:
V= abc либо трех смежных ребер: V=а 3.
Куб – одна из простейших трехмерных фигур. Каждому знакомы кубики льда, квадратные коробки или кристаллы соли – все они являются такими фигурами. Площадь поверхности куба – это общая площадь всех сторон на его поверхности. Все шесть его граней соразмерны, поэтому, зная длину одной из них, можно рассчитать боковую площадь и площадь поверхности любой фигуры.
Как найти площадь куба – что собой представляет фигура?
Куб – это трехмерная фигура, которая имеет одинаковые размеры. Его длина, ширина и высота идентичны, а каждое ребро встречает другие края под одним углом. Поиск площади поверхности куба быстрый и удобный, поскольку он состоит из конгруэнтных или соразмерных квадратов. Итак, как только вы найдете размер одного из квадратов, вы узнаете площадь всей фигуры.
Как найти площадь куба – грани фигуры
Из иллюстрации видно, что куб имеет переднюю и заднюю грань, две боковые и верхнюю с нижней стороны. Площадь любого куба будут составлять шесть конгруэнтных квадратов. Фактически, если развернуть его, можно четко увидеть шесть квадратов, которые составляют общую поверхность фигуры.


Как найти площадь куба
Площадь куба состоит из площади шести граней. Поскольку все они равны, достаточно знать площадь одной из них и умножить значение на 6. Площадь фигуры также находят по простой формуле: S = 6 x а², где «а» – одна из сторон куба.


Как найти площадь куба – установите площадь стороны
- Предположим, что высота куба составляет 2 см. Поскольку его поверхность состоит из квадратов, все его края будут иметь одинаковую длину. Поэтому, исходя из размеров высоты, его длина и ширина будут составлять 2 см.
- Чтобы найти площадь одного из квадратов, вспомните базовые знания геометрии, где S = а², где а – длина одной из сторон. В нашем случае, а = 2 см, так что S = (2 см)² = 2 см х 2 см = 4 см².
- Площадь одного из квадратов поверхности составляет 4 см². Не забудьте указать свое значение в квадратных единицах.


Как найти площадь куба – пример
Поскольку вся поверхность фигуры состоит из шести соразмерных квадратов, нужно умножить площадь одной стороны на 6, следуя формуле S = 6 x а². В нашем случае S = 6 х 4 см² = 24 см². Площадь трехмерной фигуры составляет 24 см².


Находим площадь куба, если сторона выражена в дробях
Если вам сложно работать с дробью, конвертируйте ее в десятичную.
Например, высота куба 2 ½ см.
- S = 6 х (2½ см) ²
- S = 6 х (2,5 см) ²
- S = 6 х 6,25 см ²
- S = 37,5 см ²
- Площадь поверхности куба – 37,5 см ².


Зная площадь куба, находим его сторону
Если площадь поверхности куба известна, можно определить длину его сторон.
- Площадь куба составляет 86,64 см². Необходимо определить длину грани.
- Решение. Поскольку известна площадь поверхности, нужно считать в обратном порядке, разделив значение на 6, а затем извлечь квадратный корень.
- Сделав необходимые вычисления, получаем длину 3,8 см.


Как найти площадь куба – онлайн измерение площади
Используя калькулятор на сайте OnlineMSchool , можно быстро вычислить площадь куба. Достаточно ввести нужное значение стороны и сервис выдаст детальное пошаговое решение задания.


Итак, чтобы знать площадь куба, вычислите площадь одной из сторон, затем умножьте результат на 6, так как фигура имеет 6 равных сторон. Можно при подсчете использовать формулу S = 6а². Если задана площадь поверхности, возможно определить длину боковой части, проделав обратные шаги.
Заострить на само куба. Из него видно, что любая из граней куба представляет квадрат. Таким образом, задача по нахождению площади грани куба сводится к задаче по нахождению площади любого из квадратов (граней куба). Можно любую из граней куба, так как длины всех его ребер между собой.
Пример: Длина ребра куба 11 см, требуется найти ее площадь.
Решение: зная длину грани, можно найти ее площадь:
Ответ: площадь грани куба с ребром 11 см равна 121 см²
Любой куб имеет 8 вершин, 12 ребер, 6 граней и 3 грани при вершине.
Куб – это такая фигура, которая встречается в быту невероятно часто. Достаточно вспомнить игровые кубики, игральные кости, кубики в различны детских и подростковых конструкторах.
Многие элементы архитектуры имеют кубическую форму.
Кубическими метрами принято измерять объемы различных веществ в различных сферах жизни общества.
Говоря научным языком, кубический метр – это мера измерения объема вещества, которое способно поместиться в куб с длиной ребра 1 м
Таким образом, можно ввести и иные единицы измерения объема: кубические миллиметры, сантиметры, дециметры и т.п.
Помимо различных кубических единиц измерения объема, в нефтяной и газовой промышленности возможно применение иной единицы – баррель (1м³ = 6.29 баррелей)
Если у куба известна длина ее ребра, то, помимо площади грани можно найти и другие параметры данного куба, например:
Площадь поверхности куба: S = 6*a²;
Объем: V = 6*a³;
Радиус вписанной сферы: r = a/2;
Радиус сферы, описанной вокруг куба: R = ((√3)*a))/2;
Диагональ куба (отрезок, соединяющие две противоположные вершины куба, который проходит через его центр): d = a*√3
- площадь куба если ребра равны 11 см
Кубом называют правильный многогранник, каждая грань которого является квадратом. Площадью куба называют площадь его поверхности, которая состоит из суммы площадей его граней, то есть, из суммы площадей квадратов, которые образуют куб.
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля – до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Это суммарная площадь всех поверхностей фигуры. Площадь поверхности куба равна сумме площадей всех его шести граней. Площадь поверхности является числовой характеристикой поверхности. Для вычисления площади поверхности куба, Вам необходимо знать определенную формулу и длину одной из сторон куба. Для того чтобы Вы могли оперативно вычислить площадь поверхности куба, вам необходимо запомнить формулу и сам порядок действий. Чуть ниже мы подробно разберем порядок вычисления полной площади поверхности куба и приведем конкретные примеры.
Выполняется по формуле SA = 6а 2 . Куб (правильный гексаэдр) – это один из 5 видов правильных многогранников, который является правильным прямоугольным параллелепипедом, куб имеет 6 граней, каждая из этих граней является квадратом.

Для вычисления площади поверхности куба Вам необходимо записать формулу SA = 6а 2 . Теперь давайте разберем почему данная формула имеет такой вид. Как мы говорили ранее, куб имеет шесть равных квадратных граней. Исходя из того что стороны квадрата равны, площадь квадрата составлять – a 2 , где а – сторона куба. Так куба имеет 6 равных квадратных граней, то для определения площади его поверхности, Вам необходимо умножить площадь одной грани (квадрата) на шесть. В итоге получаем формулу для вычисления площади поверхности (SA) куба: SA = 6а 2 , где а – ребро куба (сторона квадрата).
Чему равна площадь поверхности куба.
Измеряется в квадратных единицах, к примеру, в мм 2 , см 2 , м 2 и так далее. Для дальнейших расчетов Вам необходимо будет измерить ребро куба. Как мы знаем, ребра у куба равны, поэтому Вам будет достаточно измерить только одно (любое) ребро куба. Выполнить такой замер Вы можете при помощи линейки (или рулетки). Обратите внимание на единицы измерения на линейке или рулетке и запишите значение, обозначив его через а.
Пример : а = 2 см.

Полученное значение возведите в квадрат. Таким образом, Вы возведите в квадрат длину ребра куба. Для того чтобы возвести число в квадрат умножьте его на себя. Наша формула будет иметь следующий вид: SA = 6*а 2
Вы вычислили значение площади одной из граней куба.
Пример : а = 2 см
a 2 = 2 х 2 = 4 см 2
Полученное значение умножайте на шесть. Не забывайте, что у куба 6 равных граней. Определив площадь одной из граней, умножьте полученное значение на 6, чтобы все грани куба участвовали в расчете.
Вот мы и пришли к конечному действию по вычислению площади поверхности куба .
Источники:
http://www.calc.ru/Ploshchad-Poverkhnosti-Kuba.html
http://fb.ru/article/60830/kak-nayti-ploschad-poverhnosti-kuba
http://mmkspo.ru/osteohondroz/uravnenie-poverhnosti-kuba-kak-naiti-ploshchad-kuba/

{S_{полн}=6a^2}
На этой странице мы собрали формулы, которые помогут найти площадь полной и боковой поверхности куба. А чтобы упростить расчет у нас есть калькулятор, который сделает это быстро и точно.
В дополнение на сайте можно найти объем куба.
Куб – фигура, представляющая собой правильный многогранник, все грани которого являются квадратами. Все ребра (стороны) куба равны между собой.
Содержание:
- калькулятор площади поверхности куба
- площадь полной поверхности куба
- формула площади полной поверхности куба через ребро
- формула площади полной поверхности куба через диагональ грани
- формула площади полной поверхности куба через диагональ куба
- формула площади полной поверхности куба через периметр грани
- формула площади полной поверхности куба через периметр куба
- формула площади полной поверхности куба через объем
- формула площади полной поверхности куба через площадь вписанного шара
- площадь боковой поверхности куба
- формула площади боковой поверхности куба через ребро
- формула площади боковой поверхности куба через диагональ грани
- формула площади боковой поверхности куба через диагональ куба
- формула площади боковой поверхности куба через периметр грани
- формула площади боковой поверхности куба через периметр куба
- формула площади боковой поверхности куба через объем
- примеры задач
Что такое площадь полной поверхности куба
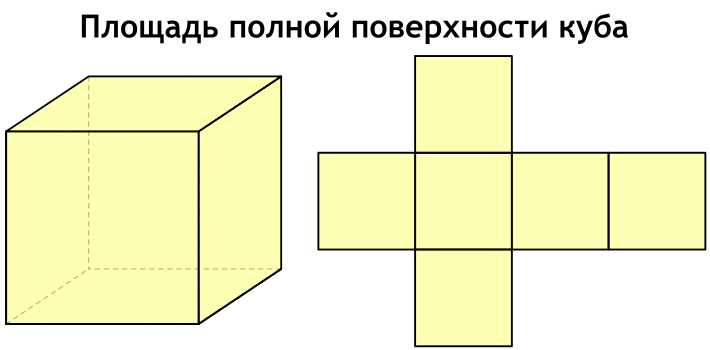
Куб состоит из сторон, которые называют гранями. Каждая такая грань представляет собой квадрат, а всего у куба 6 граней. Площади всех этих граней равны между собой и сложив все площади всех шести граней куба мы получим площадь полной поверхности куба.
Площадь полной поверхности куба – это сумма площадей всех его граней.
Площадь полной поверхности удобно представить, если посмотреть на развертку куба.
Формула площади полной поверхности куба через ребро
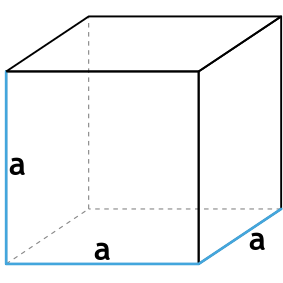
{S_{полн}=6a^2}
a – ребро куба
Формула площади полной поверхности куба через диагональ грани
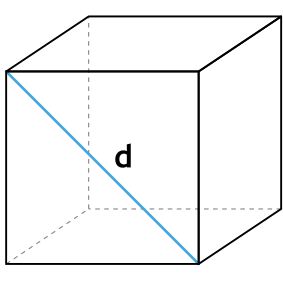
{S_{полн}=3d , ^2}
d – диагональ грани куба
Формула площади полной поверхности куба через диагональ куба
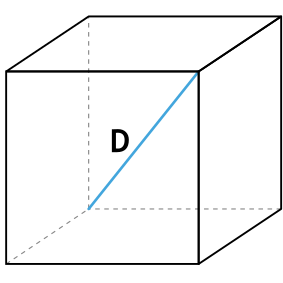
{S_{полн}=2D^2}
D – диагональ куба
Формула площади полной поверхности куба через периметр грани
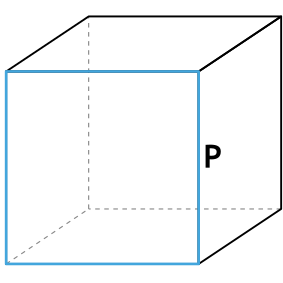
{S_{полн}= dfrac{3}{8}P^2}
P – периметр грани куба
Формула площади полной поверхности куба через периметр куба

{S_{полн}= dfrac{P^2}{24}}
P – периметр куба
Формула площади полной поверхности куба через объем
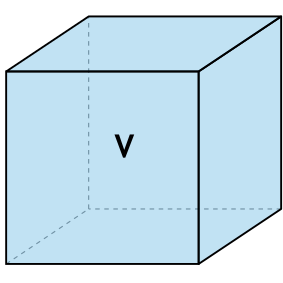
{S_{полн}= 6{(sqrt[3]{V})}^2}
V – объем куба
Формула площади полной поверхности куба через площадь вписанного шара
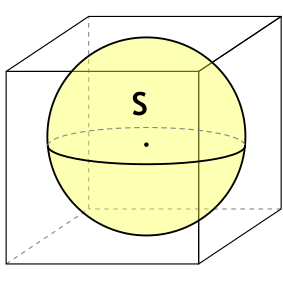
{S_{полн}= 6 dfrac{S}{pi}}
S – площадь вписанного в куб шара
Что такое площадь боковой поверхности куба
Боковая поверхность куба – сумма площадей всех его боковых граней, которых у куба четыре.
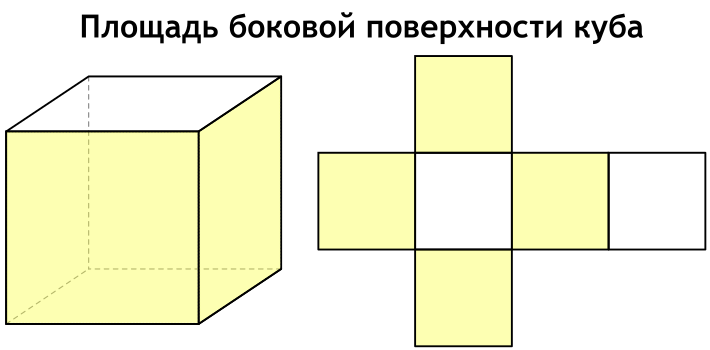
Формула площади боковой поверхности куба через ребро
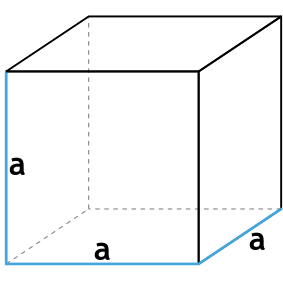
{S_{бок} = 4a^2}
a – ребро куба
Формула площади боковой поверхности куба через диагональ грани
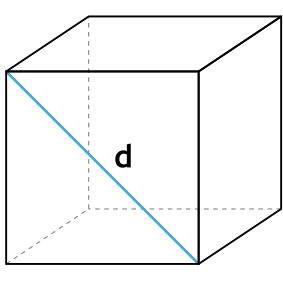
{S_{бок}=2d , ^2}
d – диагональ грани куба
Формула площади боковой поверхности куба через диагональ куба
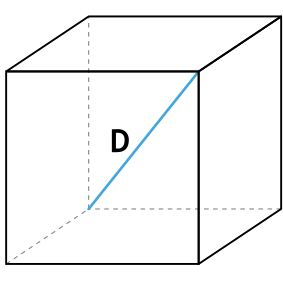
{S_{бок}=dfrac{4}{3}D^2}
D – диагональ куба
Формула площади боковой поверхности куба через периметр грани
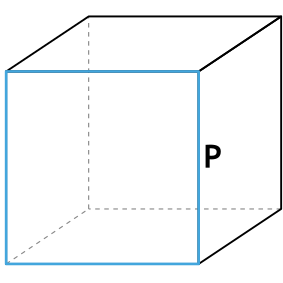
{S_{бок}= dfrac{P^2}{4}}
P – периметр грани куба
Формула площади боковой поверхности куба через периметр куба
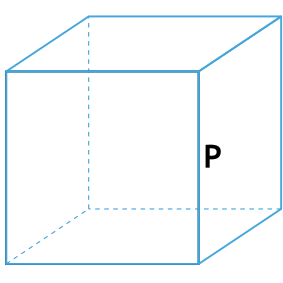
{S_{бок}= dfrac{P^2}{36}}
P – периметр куба
Формула площади боковой поверхности куба через объем

{S_{бок}= 4{(sqrt[3]{V})}^2}
V – объем куба
Примеры задач на нахождение площади поверхности куба
Задача 1
Найдите площадь поверхности куба, если его объем равен 125см³.
Решение
Для нахождения площади полной поверхности куба через его объем, нам поможет эта формула.
S_{полн} = 6{(sqrt[3]{V})}^2 = 6{(sqrt[3]{125})}^2 = 6{(5)}^2 = 6 cdot 25 = 150 : см²
Ответ: 150 см²
Проверить ответ нам поможет калькулятор .
Задача 1
Найдите площадь боковой поверхности куба с ребром 4см.
Решение
Для нахождения площади боковой поверхности куба с известной длиной ребра используем эту формулу.
S_{бок} = 4a^2 = 4 cdot 4^2 = 4 cdot 16 = 64 : см²
Ответ: 64 см²
Проверка .
Куб (или гексаэдр) — это правильный многогранник, который состоит из многоугольников, являющихся квадратами.
Онлайн-калькулятор площади поверхности куба
У куба есть двенадцать ребер, то есть, отрезков, которые являются сторонами квадратов.
Также он имеет восемь вершин и шесть граней.
У куба есть диагональ, соединяющая противоположные вершины.
Формула площади поверхности куба
Площадь поверхности куба – это сумма площадей всех его граней:
S=S1+S2+S3+S4+S5+S6S=S_1+S_2+S_3+S_4+S_5+S_6
Площадь каждой грани одинакова, то есть:
S1=S2=S3=S4=S5=S6=S′S_1=S_2=S_3=S_4=S_5=S_6=S’
S′S’ — площадь любой грани куба.
Тогда полная площадь поверхности куба запишется как:
S=6⋅S′S=6cdot S’
Рассмотрим на примерах разные способы вычисления полной площади поверхности куба.
Формула площади поверхности куба по длине ребра куба
Площадь каждой грани куба вычисляется как площадь квадрата, со стороной ребра куба по формуле:
S′=a⋅a=a2S’=acdot a=a^2
aa — сторона куба.
Отсюда, окончательно площадь поверхности куба:
S=6⋅a2S=6cdot a^2
aa — длина стороны куба.
Найти площадь поверхности куба, если длина его ребра равна 12 (см.).
Решение
a=12a=12
S=6⋅a2=6⋅122=6⋅144=864S=6cdot a^2=6cdot 12^2=6cdot 144=864 (см. кв.)
Ответ: 864 см. кв.
Формула площади поверхности куба по диагонали куба
По теореме Пифагора, диагональ куба связанна с длиной его ребра по формуле:
d2=a2+a2+a2d^2=a^2+a^2+a^2
d2=3⋅a2d^2=3cdot a^2
d=3⋅ad=sqrt{3}cdot a
Отсюда:
a=d3a=frac{d}{sqrt{3}}
Подставим в формулу для площади:
S=6⋅a2=6⋅(d3)2=2⋅d2S=6cdot a^2=6cdotBig(frac{d}{sqrt{3}}Big)^2=2cdot d^2
S=2⋅d2S=2cdot d^2
dd — диагональ куба.
Одна четвертая часть диагонали куба равна 2 (см.). Найти площадь поверхности куба.
Решение
14⋅d=2frac{1}{4}cdot d=2
Найдем диагональ:
d=4⋅2=8d=4cdot 2=8
Площадь:
S=2⋅d2=2⋅82=2⋅64=128S=2cdot d^2=2cdot 8^2=2cdot 64=128 (см. кв.)
Ответ: 128 см. кв.
Формула площади поверхности куба по длине диагонали квадрата (грани куба)
По теореме Пифагора, диагональ квадрата ll связанна с его стороной aa:
l2=a2+a2l^2=a^2+a^2
l2=2⋅a2l^2=2cdot a^2
l=2⋅al=sqrt{2}cdot a
Тогда сторона квадрата:
a=l2a=frac{l}{sqrt{2}}
Подставляем в формулу для площади и получаем:
S=6⋅a2=3⋅l2S=6cdot a^2=3cdot l^2
S=3⋅l2S=3cdot l^2
ll — диагональ квадрата (грани куба).
Одна четвертая часть диагонали квадрата равна 1 (см). Найти площадь поверхности куба, образованного данным четырехугольником.
Решение
14⋅l=1frac{1}{4}cdot l=1
Найдем диагональ квадрата:
l=4⋅1=4l=4cdot 1=4
Тогда площадь:
S=3⋅l2=3⋅42=48S=3cdot l^2=3cdot 4^2=48 (см. кв.)
Ответ: 48 см. кв.
Разберем более сложные примеры.
Формула площади поверхности куба по площади вписанного в куб шара
В куб вписан шар площади SшарS_{text{шар}}. Тогда радиус RR этого шара равен половине длины стороны куба aa:
R=a2R=frac{a}{2}
Площадь шара дается формулой:
Sшар=4⋅π⋅R2S_{text{шар}}=4cdotpicdot R^2
Отсюда найдем радиус шара:
R=Sшар4⋅πR=sqrt{frac{S_{text{шар}}}{4cdotpi}}
Сторона грани куба:
a=2⋅R=2⋅Sшар4⋅πa=2cdot R=2cdotsqrt{frac{S_{text{шар}}}{4cdotpi}}
Наконец площадь поверхности куба:
S=6⋅a2=6⋅SшарπS=6cdot a^2=frac{6cdot S_{text{шар}}}{pi}
S=6⋅SшарπS=frac{6cdot S_{text{шар}}}{pi}
SшарS_{text{шар}} — площадь шара, вписанного в куб.
В куб вписан шар, площадь которого равна 64 “пи” (см. кв.). Найти полную площадь поверхности куба.
Решение
Sшар=64πS_{text{шар}}=64pi
По формуле:
S=6⋅Sшарπ=6⋅64⋅ππ=384S=frac{6cdot S_{text{шар}}}{pi}=frac{6cdot 64cdotpi}{pi}=384 (см. кв.)
Ответ: 384 см. кв.
Не знаете, кто сможет решить контрольную работу на заказ для вас? Наши эксперты с удовольствием окажут вам помощь!
Тест по теме “Площадь поверхности куба”
Содержание
- – Как узнать площадь куба формула?
- – Как найти сторону куба через площадь его поверхности?
- – Как найти объем куба и площадь его поверхности?
- – Как найти S бок Куба?
- – Как из куба вычислить квадрат?
- – Чему равна периметр куба?
- – Сколько сторон у куба?
- – Как вычислить объем куба?
- – Как найти площадь поверхности шара?
- – Как найти площадь по объему?
- – Как найти диагональ куба если известен его объем?
- – Как найти диагональ куба зная его сторону?
- – Как найти S полное?
- – Чему равно S боковое?
- – Как найти S осн пирамиды?
Как узнать площадь куба формула?
Площадь поверхности куба равна квадрату длины его грани умноженному на шесть (куб имеет шесть одинаковых граней). где S – площадь куба, a – длина грани куба.
Как найти сторону куба через площадь его поверхности?
Чтобы найти сторону куба если известна площадь его грани, извлеките из числового значения площади грани квадратный корень. В виде формулы эту зависимость можно записать в следующем виде:С = √П, где:С – длина стороны (грани) куба, П – площадь грани куба.
Как найти объем куба и площадь его поверхности?
У куба шесть квадратных граней, которые пересекаются под прямым углом и стороны которых равны. Вычислить объем куба легко — нужно перемножить длину, ширину и высоту. Так как у куба длина равна ширине и равна высоте, то объем куба равен s3, где s — длина одного (любого) ребра куба.
Как найти S бок Куба?
Боковая поверхность куба состоит из 4 граней, а полная поверхность включает в себя еще два основания в виде таких же квадратов. Поэтому чтобы найти площадь боковой поверхности куба умножаем площадь данного квадрата на 4, а чтобы найти площадь его полной поверхности – на 6.
Как из куба вычислить квадрат?
Так куба имеет 6 равных квадратных граней, то для определения площади его поверхности, Вам необходимо умножить площадь одной грани (квадрата) на шесть. В итоге получаем формулу для вычисления площади поверхности (SA) куба: SA = 6а2, где а – ребро куба (сторона квадрата).
Чему равна периметр куба?
Формулы
| Периметр куба (общая длина ребра) | O = | 12 × a |
|---|---|---|
| Площадь одной стороны | P = | a × a = a² |
| Площадь куба (поверхность) | Q = | 6 × P1 = 6 × a² |
| Объем куба | V = | a × a × a = a³ |
| Диагоналная (стороны/стены) | u2 = | a √2 ≈ a × 1,41 |
Сколько сторон у куба?
Правильно, у куба 6 граней. Стороны граней (квадратов) называют ребрами куба.
Как вычислить объем куба?
Формула вычисления объема куба
- Через длину ребра Объем (V) куба равняется произведению его длины на ширину на высоту. Т. к. …
- Через длину диагонали грани Как мы знаем, грани куба равны между собой и являются квадратом, сторона которого может быть найдена через длину диагонали по формуле: a=d/√2.
Как найти площадь поверхности шара?
Формулы площади шара:
- Площадь поверхности шара равна четырем его радиусам в квадрате умноженным на число π. S = 4 π R2
- Площадь поверхности шара равна квадрату его диаметра умноженного на число π. S = π D2
Как найти площадь по объему?
к. площадь (S) – это произведение длинны и ширины (S= l*b), а объем – произведение длины, ширины и высоты. Подставьте в формулу вычисления объема вместо l*b площадь. Вы получите выражение V=S*h.
Как найти диагональ куба если известен его объем?
Объем куба равен длине ребра, возведенной в третью степень.
- V = a3 , где Y — объем куба, а — ребро куба. Если известен объем куба V, длину ребра (а) рассчитываем по формуле: …
- d = a√3 , где а — ребро куба, d — диагональ куба. …
- a = d/√3 , Диагональ куба d.
Как найти диагональ куба зная его сторону?
Для определения диагонали куба вписываем в куб прямоугольный треугольник, соединив диагональ куба, диагональ основания и боковое ребро, исходящее из вершины основания. Воспользовавшись теоремой Пифагора, вычисляем диагональ куба, которая равна произведению ребра куба (а) на корень квадратный из трех.
Как найти S полное?
Sполн. =
Площадь боковой поверхности прямой призмы равняется произведению периметра ее основания на высоту.
Чему равно S боковое?
Различают два вида площадей поверхности тел: Sбок — площадь боковой поверхности тела, и Р — площадь полной поверхности тела, которая равна сумме площадей боковой поверхности и основания тела.
Как найти S осн пирамиды?
Площадь (S) полной поверхности пирамиды равняется сумме площади ее боковой поверхности и основания. Боковой гранью правильной пирамиды является равнобедренный треугольник. Формула площади основания правильной пирамиды зависит от вида многогранника.
Интересные материалы:
Сколько можно хранить вареные лисички?
Сколько можно хранить вареные шампиньоны в холодильнике?
Сколько можно хранить замороженную капусту?
Сколько можно набрать мышечной массы за 3 месяца?
Сколько можно находиться на Бали россиянам?
Сколько можно находится на территории России?
Сколько можно находится в РФ без регистрации?
Сколько можно находиться за границей с видом на жительство?
Сколько можно обменять евро за один раз?
Сколько можно перевозить валюты через границу России?
