|
Площадь фигуры (треугольник, четырёхугольник, трапеция и др.) по клеточкам (клеткам). Какие есть формулы?
Есть способ, при котором надо воспользоваться формулой, основой которой будет понятие узла, узла внутреннего и узла внешнего. Узел это пересечение линий, образующих эти самые клеточки. Внешние узлы, это узлы, находящиеся на сторонах и вершинах геометрических фигур, площади которых нам надо найти. А внутренние узлы, это узлы внутри этих фигур. Клеточки у нас со сторонами равными одному сантиметру (1 см). Формула, о которой идет речь, называется формула Пика. Выглядит она вот так:
И по ней очень просто посчитать площадь фигуры S. В этой формуле M это количество внешних узлов, N – количество внутренних узлов. Приведем пример, возьмем геометрическую фигуру параллелограмм:
Внутренние узлы – синие – N – их у нас 20. Внешние узлы – красные – М – их у нас 18 и их количество нам надо поделить на два, получится 18/2 = 9 узлов. Складываем 9 + 20 и вычитаем единицу: 20 + 9 – 1 = 28 см². Еще один пример:
S = 14/2 + 43 – 1 = 49 см². система выбрала этот ответ лучшим
Ксарфакс 6 лет назад Допустим, у нас есть произвольная фигура, построенная на листе в клетку. Необходимо вычислить её площадь. Площадь фигуры по клеточкам Для того, чтобы найти площадь любой фигуры по клеточкам, можно использовать формулу Пика. Данная формула основана на подсчёте количества узлов, лежащих внутри фигуры и на её границе. Узел – это точка, которая лежит на пересечении 2 линий данной сетки: вертикальных и горизонтальных. Площадь фигуры по клеточкам находится по формуле:
N – количество узлов, которые находятся внутри фигуры. M – количество узлов, которые находятся на границах (на вершинах и сторонах). Примеры нахождения площади по клеточкам 1) Найдём площадь треугольника. Будем считать, что одна клетка – это 1 см. Отметим внутренние узлы и узлы, которые находятся на границах.
N = 7 (внутренние). M = 8 (узлы на границах). Площадь треугольника S = 7 + 8/2 – 1 = 10 см². 2) Найдём площадь трапеции по клеточкам, одна клетка – это 1 см. Отметим все узлы и подсчитаем их количество.
N = 11 (внутренние). M = 12 (узлы на границах). Площадь трапеции S = 11 + 12/2 – 1 = 16 см². 3) Найдём площадь произвольного многоугольника. Одна клетка – это 1 см. Отметим внутренние узлы и узлы, расположенные на границах фигуры. Подсчитаем их количество.
N = 6 (внутренние узлы). M = 8 (узлы на границах). Площадь многоугольника S = 6 + 10/2 – 1 = 10 см².
Марина Вологда 3 года назад Такие задачи очень часто встречаются, когда известен размер клеточки и дана фигура. Вот пример таких задач:
Решение зависит от того, какая фигура дана и как именно она размещена относительно клеточек. Возьмем простой пример, необходимо вычислить площадь вот такого треугольника:
Вспоминаем правило: Теперь считаем, сколько клеточек треугольник в длину и сколько в высоту. У нас получается 2 в высоту и 6 в длину. Подставляем к формуле: S = 1/2 х 2 х 6 = 6 см2. Считаем по клеточкам, подставляя формулу Пика:
Целых клеточек у нас 3. Теперь считаем, сколько не целых: 6. Делим их на 2. S = 3 + 6:2 = 6 см2. А теперь высчитываем по формуле Пика: количество узлов сетки внутри – 2, количество узлов сетки, лежащих на границах – 10. Подставляем к формуле и получаем – 2 + 10:2 – 1 = 6 см2. Теперь давайте рассмотрим вот такой треугольник:
Чтобы найти площадь, вспоминаем правило: Считаем клеточки и подставляем в формулу: S = 1/2 х 2 х 6 = 6 см2. А теперь находим по клеточкам: целых клеточек 2, не целых клеточек 8. Подставляем в формулу: 2 + 8:2 = 6 см2. Пробуем сделать по формуле Пика: количество узлов сетки внутри – 3, количество узлов сетки, лежащих на границах – 8. Подставляем к формуле и получаем – 3 + 8:2 – 1 = 6 см2.
Enot-Nina 3 года назад Найти площадь геометрической фигуры можно самыми разными способами: Самый простой вариант – это вручную посчитать клеточки – целые и половинки также поскладывать. Простой, хотя и не самый быстрый и может не самый точный способ, но он работает. Чтобы легче было считать, достаточно расчертить фигуру на более простые. Есть еще один способ – это использовать давно разработанную формулу. Это так называемая формула Пика. Для нее нужно посчитать количество узлов – точек пересечения клеточек, что окружены фигурой (находятся внутри нее), а также подсчитать количество пограничных узлов – по контуру фигуры. Вот на картинке наглядно показано, как ее можно применять, чтоб посчитать площадь любой фигуры по клеточкам:
Бархатные лапки 3 года назад Площадь любого многоугольника можно посчитать по клеточкам. Для этого применяем формулу Пика. На нашем рисунке В – количество узловых клеточек внутри фигуры, Г – количество узлов на границе . Узлы – пересечение двух линий. многоугольника. Площадь равна S = В + Г/2 – 1 Считаем точки на рисунке и подставляем в формулу. – 10 + 7/2 -1 = 12,5. Таким образом можно посчитать площадь, если вершины фигуры лежат в узлах.
Ann Luka 6 лет назад Чтобы найти площадь фигуры по клеточкам, нужно посчитать сколько в фигуре целых клеточек. Потом нужно посчитать сколько не целых и поделить их количество на 2. Добавить к получившемуся числу количество целых клеточек – это и будет правильный ответ. Например. В треугольнике 3 целых клетки и 4 не целых. 3+4/2=5 пощадь треугольника 5 клеток.
Outline 3 года назад Для того, чтобы определить площадь фигуры на бумаге в клеточку есть универсальная формула Пика, позволяющая вычислить площадь изображения, но в только в том случае, если вершины искомой фигуры имеют целые (натуральные числа) координаты. Называется эта формула, в честь Георга Пика: S=В + Г / 2 − 1 В этой формуле буквенные обозначения означают следующее: В — количество целочисленных точек внутри многоугольника; Г — количество целочисленных точек на границе (вершинах и сторонах) многоугольника; S – площадь фигуры. Здесь используется понятие “целочисленные” – это те, точки, которые расположены на пересечениях сетки (в ее узлах). Для примера, найдем площадь треугольника:
Обозначим внутренние точки нашей фигуры красными кружками, а те, что на границах – синим цветом. Считаем красные и синие точки: В=12, Г=4. Исходя из подсчетов определяем площадь треугольника по формуле: S=В+Г/2-1=12+2-1=13. Можно убедиться в правильность проведенных выше расчетах. Рассчитываем площадь квадрата, обведенного красным, и вычитаем площади зеленого, синего и фиолетового треугольников:
S квадрата равна 36, площади треугольников: синего – 6, зеленого – 2, фиолетового – 15. Исходя из полученных данных, S белого треугольника равна 13: S=36-6-15-2=13.
KritikSPb 3 года назад Подсчет клеточек – дело полезное. С их помощью можно найти площадь геометрической фигуры. Достаточно воспользоваться формулой, доказанной Георгом Пиком в 1899 году. Подходит для расчета площади фигур с прямыми сторонами и целым количеством углов, чаще всего применяют для нахождения площади разносторонних треугольников и многоугольников с числом углов больше 4-х. На теорему Пика есть задания в ЕГЭ.
127771 3 года назад Сначала я подумал, что нужно будет фигуру, которая указана на рисунке в клеточку разбить по фигурам так, чтобы можно посчитать площадь каждой фигуры по-отдельности, но оказалось все намного проще. Существует для данной задачи специальная формула Пика, которая выглядит следующим образом: Площадь = В + Г/2 – 1, где:
Теперь разберемся на примере, у нас есть такой пример:
Перед нами трапеция. Допустим площадь одной клетки 1 кв.см. Теперь можно воспользоваться формулой: 11+12/2-1=16 кв.см.
Бекки Шарп 3 года назад Найти площадь фигуры можно если вершины фигуры находятся в уголках клеточек, так называемые Целочисленные вершины или узловые точки. Решать задачу будем по формуле Пика, где
Вот такая фигура у нас –
Считаем точки и подставляем в формулу: S = 17 + 14/2 – 1 = 23 Ответ мы получаем в квадратных единицах, то есть клеточках. Знаете ответ? |
Всем привет,мои юные и не очень любители пошуршать мозгами! 🧠
Сегодня поговорим о задачах с фигурами,но не простыми,а на квадратной решетке. 🤓
Такого рода задачи часто попадаются на ОГЭ,поэтому рекомендую дочитать ЭТО ЧУДО до конца 🙂
Длина средней линии трапеции
Решим задачу с этой самой длиной. На клетчатой бумаге 1×1 изображена вот такая трапеция:
Найдем длину ее средней линии.
Сосчитаем клеточки оснований:
7 снизу,3 сверху.
Их складываем.
А потом делим ответ на 2:
Ответ: 5
Расстояние от и до
Теперь про более странную задачу поговорим.
На клетчатой бумаге 1×1 отмечены три точки: A,B и C.
Нужно найти расстояние от точки A до середины отрезка BC.
Нужно ПРОСТО сосчитать три клетки до середины! ВСЕ!
Ответ: 3
Площадь ромба
На той же бумаге начертили ромб.
Нужно найти его площадь.
Как? Оч просто!
Нужно сделать из этого ромба прямоугольник:
А теперь посчитаем клеточки у сторон:
Площадь ромба равна половине произведения его диагоналей.
Ответ: 20.
Площадь странной фигуры
На этой же (ОПЯТЬ?!ААА!) бумаге Вася начертил странную фигуру. А мы должны найти ее площадь…)
Теперь внимание! Нужно просто посчитать квадратики! Считаем…
Ответ: 11
Длина большей диагонали ромба
Опять ромб. Только теперь нужно найти не площадь,а длину большей диагонали.
Давайте посчитаем:
Ответ: 8
Повторим расстояния…
Опять нужно найти расстояние от точки А,до прямой BC.
Проведем прямую от точки между точками B и C.
А теперь проведем линию от точки A,до отрезка ВС.
Ответ: 1
Площадь параллелограмма
Найдем площадь параллелограмма.
Как ее искать?
Нужно умножить высоту на основание:
Ответ: 20
Длина средней линии треугольника
У нас есть вот такой треугольник:
Нужно найти длину его средней линии,параллельной стороне AC.
Для этого мы узнаем длину основания и разделим ее на 2.
Ответ: 2
Длина большего катета
Нам дан такой прямоугольный треугольник:
Нужно найти длину его большего катета.
Вспомним про стороны прямоугольного треугольника:
Катет b (основание) больше. Он имеет 10 клеток,а катет а 5.
Ответ: 10.
На этом все!
Ждите более сложные задания в следующем посте!
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
На рисунке изображена фигура.
=Найди её площадь, если сторона одной клетки равна 1 см.
1
Тип 5.2 № 533 

i
На рисунке изображена фигура.
Начертите прямоугольник с такой же площадью, каждая из сторон которого больше 1 см.
2
На рисунке изображена фигура.
Найди её площадь, если сторона одной клетки равна 1 см.
1
Тип 5.2 № 534 

i
На рисунке изображена фигура.
Начертите прямоугольник с такой же площадью, каждая из сторон которого больше 1 см.
3
На рисунке изображена фигура.
Найди её площадь, если сторона одной клетки равна 1 см.
1
Тип 5.2 № 535 

i
На рисунке изображена фигура.
Начертите прямоугольник с такой же площадью, каждая из сторон которого больше 1 см.
4
На рисунке изображена фигура.
Найди её площадь, если сторона одной клетки равна 1 см.
1
Тип 5.2 № 536 

i
На рисунке изображена фигура.
Начертите прямоугольник с такой же площадью, каждая из сторон которого больше 1 см.
5
Тип 5.1 № 301 

i
На рисунке изображён четырёхугольник.
Найди площадь данного на рисунке четырёхугольника.
Источник: Всероссийская проверочная работа математика 4 класс 2017 года. А. А. Мальцев, Д. А. Мальцев. Вариант 12.
1
Тип 5.2 № 543 

i
На рисунке изображён четырёхугольник.
Дострой этот четырёхугольник до прямоугольника.
Источник: Всероссийская проверочная работа математика 4 класс 2017 года. А. А. Мальцев, Д. А. Мальцев. Вариант 12.
Пройти тестирование по этим заданиям
![]()
Формула Пика. Рассказ о формуле, при помощи которой можно находить площадь фигуры построенной на листе в клетку (треугольник, квадрат, трапеция, прямоугольник, многоугольник). Это формула Пика.
Она секретной не является. Информация о ней в интернете имеется, но многим материал статьи будет крайне полезен. Об этой формуле обычно рассказывается применительно к нахождению площади треугольника. На примере треугольника мы её и рассмотрим.
В задачах, которые будут на ЕГЭ есть целая группа заданий, в которых дан многоугольник построенный на листе в клетку и стоит вопрос о нахождении площади. Масштаб клетки это один квадратный сантиметр.
ФОРМУЛА ПИКА
Площадь искомой фигуры можно найти по формуле:
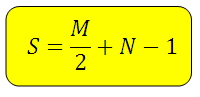
М – количество узлов на границе треугольника (на сторонах и вершинах)
N – количество узлов внутри треугольника
*Под «узлами» имеется ввиду пересечение линий.
Найдём площадь треугольника:

Отметим узлы:

1 клетка = 1 см
M = 15 (обозначены красным)
N = 34 (обозначены синим)


Ещё пример. Найдём площадь параллелограмма:

Отметим узлы:

M = 18 (обозначены красным)
N = 20 (обозначены синим)


Найдём площадь трапеции:

Отметим узлы:

M = 24 (обозначены красным)
N = 25 (обозначены синим)


Найдём площадь многоугольника:

Отметим узлы:

M = 14 (обозначены красным)
N = 43 (обозначены синим)

Понятно, что находить площадь трапеции, параллелограмма, треугольника проще и быстрее по соответствующим формулам площадей этих фигур. Но знайте, что можно это делать и таким образом.
А вот когда дан многоугольник, у которого пять и более углов эта формула работает хорошо.
Теперь взгляните на следующие фигуры:

Это типовые фигуры, в заданиях стоит вопрос о нахождении их площади. Такие или подобные им будут на ЕГЭ. При помощи формулы Пика такие задачи решаются за минуту. Например, найдём площадь фигуры:


Отметим узлы:

M = 11 (обозначены красным)
N = 5 (обозначены синим)

Ответ: 9,5
![]()
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.

Посмотреть решение
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.

Посмотреть решение
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.

Посмотреть решение
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.

Посмотреть решение
Конечно, можно и эти «микрофигурки» дробить на более простые фигуры (треугольники, трапеции). Способ решения выбирать вам.
Рассмотрим подход оговоренный в статье “Площадь четырёхугольника. Универсальный способ“.
Найдём площадь фигуры:

Опишем около неё прямоугольник:

Из площади прямоугольника (в данном случае это квадрат) вычтем площади полученных простых фигур:

Ответ: 4,5
В будущем будем рассматривать задания на нахождение площади, связанные с окружностями построенными на листе в клетку, не пропустите! На этом всё. Успехов вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Ученик
(201),
закрыт
9 лет назад
Naumenko
Высший разум
(856086)
9 лет назад
1.полезно скопировать рисунок на клетчатую бумагу,
причем сделать так:
сначала просчитать длины сторон по максимуму.
те без вырезов-высота (ширина) 6 кл
длина 10 кл.
теперь посчитать 6*10
начинаем “отрезать”-отчеркивать и попутно считаем . сколько –
2 раза по 4 кл и 1 раз одну.
итого -9кл.
аналогичный прием для задания 8.
в кв. см. если 2 клетки 1 см рассчитывается.





















