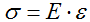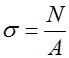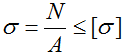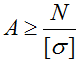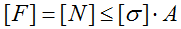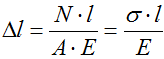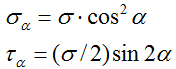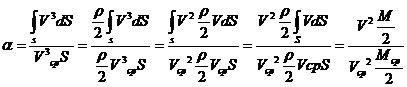iSopromat.ru
Подборка формул для расчета элементов и конструкций на растяжение-сжатие и решения задач сопротивления материалов по расчету нормальных напряжений, деформаций и перемещения сечений стержней при продольном нагружении.
Обозначения в формулах:
Формула для расчета напряжений в поперечном сечении стержня
Расчет минимальной площади поперечного сечения бруса
Расчет допустимой величины внешней растягивающей/сжимающей силы (определение грузоподъемности)
Расчет перемещения сечений
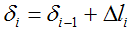
Здесь: δ i — перемещение рассматриваемого сечения,
δ i-1 — перемещение предыдущего сечения,
Δ li — деформация участка между указанными сечениями.
Здесь α — угол отклонения сечения от поперечного.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Тема 2.2. Растяжение и сжатие
Под растяжением (сжатием) понимают такой вид нагружения, при котором в поперечных сечениях стержня возникают только продольные силы N, а прочие силовые факторы (поперечные силы, крутящий и изгибающий моменты) равны нулю.
Это самый простой и часто встречающийся вид деформации. Обычно он наблюдается когда внешняя нагрузка действует вдоль продольной оси стержня. Продольной осью стержня называется линия, проходящая через центры тяжести поперечных сечений.
Обычным является растяжение стержня силами, приложенными к его концам. Передача усилий к стержню может быть осуществлена различными способами, как это показано на рис. 1.
Рис. 1. Растяжение стержня
Во всех случаях, однако, система внешних сил образует равнодействующую F, направленную вдоль оси стержня. Поэтому независимо от условий крепления растянутого стержня, расчетная схема в рассматриваемых случаях (рис. 1, а, б) оказывается единой (рис. 1, в) согласно принципу Сен – Венана.
Если воспользоваться методом сечений (рис. 2), то становится очевидным, что во всех поперечных сечениях стержня возникают нормальные силы Nz, равные силе F (рис. 2, б).
Сжатие отличается от растяжения, формально говоря, только знаком силы Nz. При растяжении нормальная сила Nz направлена от сечения (рис. 2, б), а при сжатии – к сечению.
Рис. 2. Нормальная сила N
Растягивающие продольные силы принято считать положительными (рис. 3, а), а сжимающие – отрицательными (рис. 3, б).
Рис. 3. Знак продольной силы N
При расчете стержней, испытывающий деформацию растяжения, на прочность и жесткость при статическом действии нагрузки, надо решить две основные задачи. Это определение напряжений (от Nz), возникающих в стержне, и нахождение линейных перемещений в зависимости от внешней нагрузки.
Продольные силы (Nz), возникающие в поперечных сечениях стержня, определяются по внешней нагрузке с помощью метода сечений.
График, показывающий изменение продольных сил по длине оси стержня, называется эпюрой продольных сил (эп. Nz). Он дает наглядное представление о законе изменения продольной силы.
Осью абсцисс служит ось стержня. Каждая ордината графика – продольная сила (в масштабе сил) в данном сечении стержня.
Эпюра позволяет определить, в каком сечении действует максимальное внутреннее усилие (например, найти Nmax при растяжении-сжатии). Сечение, где действует максимальное усилие будем называть опасным.
Перед построением эпюр необходимо освободить брус, в котором будем строить эпюры от опорных связей (выделить объект равновесия) и приложить к нему все действующие внешние силы (активные и реактивные). Затем необходимо установить границы участков, в пределах которых закон изменения внутренних сил постоянный. Границами таких участков являются сечения, где приложены сосредоточенные силы или начинается и кончается распределенная нагрузка, а также сечения, где имеется перелом стержня.
Применяя метод сечений и учитывая правила знаков изложенные выше, получаем уравнения изменения внутренних сил в пределах длины каждого участка бруса. Затем, используя, полученные зависимости строим графики (эпюры) этих усилий. Ординаты эпюр в определенном масштабе откладываем от базисной линии, которую проводим параллельно оси бруса.
На основании метода сечений продольная сила в произвольном поперечном сечении стержня численно равна алгебраической сумме проекций внешних сил, приложенных к стержню по одну сторону от рассматриваемого сечения, на его продольную ось.
Причем проекция внешней силы берется со знаком плюс, если сила растягивает часть стержня от точки ее приложения до рассматриваемого сечения и, наоборот, со знаком минус – если сжимает.
§2. Напряжение в поперечных сечениях стержня
При растяжении или сжатии осевыми силами стержней из однородного материала поперечные сечения, достаточно удаленные от точек приложения внешних сил ,остаются плоскими и перемещаются поступательно в направлении деформации. Это положение называют – гипотезой плоских сечений. На основании указанного можно заключить, что все точки какого-либо поперечного сечения стержня находятся в одинаковых условиях и, следовательно, напряжения распределяются по сечению равномерно. Эти напряжения перпендикулярны поперечному сечению, а значит, являются нормальными напряжениями. Их значения найдем, разделив продольную силу N на площадь А: σ=N/A
Продольная сила N с помощью метода сечений всегда может быть выражена через внешние силы. В формулe следует подставлять алгебраическое значение N т.е со знаком плюс в случае растяжения и со знаком минус в случае сжатия
§3. Расчеты на прочность и жесткость при растяжении-сжатии
Прочность стержня при осевом растяжении и сжатии обеспечена, если для каждого его поперечного сечения наибольшее расчетное (рабочее) напряжение σ не превосходит допускаемого [σ] : σ=N/A≤ [σ],
где N – абсолютное продольной силы в сечении;
А – площадь поперечного сечения;
[σ] – допускаемое напряжение пр растяжении или сжатии для материала стержня.
Данное выражение определяет условие прочности при растяжении или сжатии.
С помощью этой формулы решается три вида зада (выполняется три вида расчета):
1. Проверка прочности (проверочный расчет). При заданных продольной силы N и площади поперечного сечения А определяют рабочее (расчетное) напряжение и сравнивают его с допускаемым [σ].
Превышение рабочего (расчетного) напряжения не должно быть больше 5% , иначе прочность рассчитываемой детали считается недостаточной.
В случаях, когда рабочее напряжения значительно ниже допускаемых σ
Расчет стержней на растяжение – сжатие
Задача (выбор варианта задачи ↓ )
– построить эпюры внутренних продольных сил N и нормальных напряжений для стержня;
– рассчитать перемещения характерных сечений стержня и построить их эпюру;
– рассчитать деформации участков и общее изменение длины стержня.
► Условие прочности при растяжении. Типы задач:
1. Проверка на прочность: a) через допускаемые напряжения;
b) если задан допускаемый коэффициент запаса прочности.
2. Подбор размеров сечения (проектировочный расчет)
3. Определение грузоподъемности стержня (определение допускаемой нагрузки)
Исходные данные
| № | Площадь сечения | Длина ступени |
Основные обозначения, принятые в сопромате
Основные обозначения, принятые в сопромате
Для обозначения понятий в сопромате существует сложившаяся в мировой системе практика обозначений на основе Стандарта ИСО № 3898 (Международная организация по стандартизации, ИСО (International Organization for Standardization,ISO), занимающаяся выпуском стандартов), в которой предусмотрено применение латинских и греческих букв, специальных обозначений и т.д.
А – площадь поперечного сечения, (м 2 ); a – размер стороны прямоугольника, (м); b – ширина сечения, (м); D – диаметр наружный сечения, (м); d – диаметр внутренний сечения, (м); E – модуль упругости I рода, модуль Юнга, (Па); F – внешняя сила (H); G – модуль сдвига, (Па); g – ускорение свободного падения (м/с 2 ); h – высота сечения, (м); i – индекс у сил и усилий; l – длина стержня или силового участка, (м); M – сосредоточенный момент, Нм; N – нормальная или продольная сила (внутренняя), (H); n – коэффициент запаса прочности; [n] – допускаемый коэффициент запаса прочности; Q (QX, QY) – поперечная сила (внутренняя), (H); q – погонная нагрузка, (Н/м); R – равнодействующая сил, (Н); x – горизонтальная ось сечения; y – вертикальная ось сечения; х0, у0 – центральные оси сечения; [σ] или σadm – допускаемое напряжение, (Па); σк – критическое напряжение, Па; – ; – ; τ(τxy ,τyz ,τzx) – касательное напряжение (тау), (Па); Δl – абсолютная линейная деформация (удлинение или укорочение), (м); ε – относительная линейная деформация (эпсилон), безразмерная; σ (σx ,σy ,σz) – нормальное напряжение (сигма)(Па); δ – перемещение (дельта) (линейное, м; угловое, рад); λ – гибкость стержня (лямбда), безразмерная; ν – коэффициент Пуассона (ню), безразмерная;
Изменения обозначений, принятых в сопромате, в соответствии с рекомендациями ИСО.
[spoiler title=”источники:”]
http://www.sites.google.com/site/tehmehprimizt/lekcii/soprotivlenie-materialov/rastazenie-i-szatie
http://kramportal.info/sopromat.php
[/spoiler]
Подборка формул для расчета элементов и конструкций на растяжение-сжатие и решения задач сопротивления материалов по расчету нормальных напряжений, деформаций и перемещения сечений стержней при продольном нагружении.
Обозначения в формулах:
σ — нормальные напряжения,
N – внутренняя продольная сила,
A – площадь поперечного сечения,
[σ] – допустимые напряжения,
E – модуль продольной упругости,
ε — относительные деформации.
Закон Гука:
Формула для расчета напряжений в поперечном сечении стержня
Условие прочности (проверочный расчет) при растяжении-сжатии
Расчет минимальной площади поперечного сечения бруса
Расчет допустимой величины внешней растягивающей/сжимающей силы (определение грузоподъемности)
Формула для расчета абсолютных деформаций
Расчет перемещения сечений
Здесь: δi — перемещение рассматриваемого сечения,
δi-1 — перемещение предыдущего сечения,
Δli — деформация участка между указанными сечениями.
Напряжения в наклонных сечениях
Здесь α — угол отклонения сечения от поперечного.
Другие формулы >
Примеры решения задач >
Краткая теория >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Привет! В этом уроке начнём знакомиться с таким видом деформации, как растяжение (сжатие). Обычно, с этой темы и начинают изучать сопротивление материалов — объясняются основные понятия, которые дальше используются на протяжении всего обучения.
Задание, которое будем рассматривать в этой статье, как правило, дается студентам в первую очередь в качестве домашней работы. После изучения материалов этого урока ты научишься строить следующие эпюры: продольных сил, нормальных напряжений, а также осевых перемещений поперечных сечений. Не пугайся мудрёных названий, на самом деле, все эти эпюры строятся очень просто!
Что же давай приступим к изучению!
Построение эпюры продольных сил
В качестве примера возьмём простенькую расчётную схему стержня (также часто ступенчатый стержень, который работает на растяжение или сжатие, называют брусом). Загрузим наш стержень сосредоточенными силами, вот так:

Теперь наша первостепенная задача – построить эпюру продольных сил. И давай сразу будем разбираться в терминологии.
Что такое эпюра?
Эпюра – это график, который принято строить для визуализации распределения какой-либо величины. В нашем случае, продольной силы.
Построив такой график, мы можем увидеть, где определённая величина достигает максимальных или минимальных значений, что может быть полезно при проведении прочностных расчётов и других. Кроме того, эпюры могут служить вспомогательными инструментами для построения других эпюр, о чём мы будем говорить далее.
Что такое продольная сила?
Продольная сила – это внутренняя сила, которая возникает в сечениях стержня, работающего на растяжение или сжатие под действием внешней нагрузки.
Расчёт эпюры продольных сил
Чтобы построить эпюру продольных сил, нужно разбить брус на несколько участков, где эпюра будет иметь постоянное значение. Конкретно, для этого стержня, границами участков служат те точки, где прикладываются сосредоточенные силы.
То есть для нашего примера, нужно рассмотреть всего 2 участка:

Важно! Эпюра продольных сил, никак не зависит от формы бруса, в отличие от других эпюр, которые будем дальше рассчитывать.
Правило знаков для продольных сил
Правило знаков для продольных сил следующее:
- если внешняя сила (F) растягивает брус, то продольная сила (N) в сечениях будет положительная;
- если внешняя сила (F) сжимает брус, то продольная сила (N) в сечениях будет отрицательная.

Расчёт продольных сил на участках
На первом участке сила F1 растягивает брус на величину 5 кН, поэтому на этом участке, продольная сила будет положительной и равной:
Откладываем это значение на графике — эпюре. Эпюры, принято заштриховывать перпендикулярно к нулевой линии, а также указывать знак продольной силы:

На втором же участке, помимо силы F1, также действует сила F2, которая сжимает брус, поэтому в уравнении ее нужно учесть со знаком «минус»:
Откладываем полученное значение на эпюре:

Расчёт реакции в жёсткой заделке
Прежде всего, следует разобраться с тем, что вообще такое реакция. Всё дело в том, что помимо внутренних усилий, возникающих внутри нагруженного элемента конструкции, в том месте, где закреплён этот элемент, также возникают некоторые силы (сила), которые являются реакцией на внешнюю нагрузку и удерживающие эту конструкцию в состоянии статического равновесия.
Например, стул на котором ты сейчас сидишь и давишь на него своим весом, сопротивляется, чтобы удерживать тебя в состоянии равновесия. Если переводить на язык сопромата, твой вес в этом случае это внешняя сила, а сила с которой стул реагирует на твой вес – это реакция опоры, равная по модулю этой силе, но противоположно направленная.
Так и в нашей конструкции, в жёсткой заделке, также возникает реакция! Осталось только научиться — определять эту силу. Так как она должна компенсировать всю нагрузку, которая приложена к стержню, условие равновесия для нашей схемы можно записать так:
То есть, так как система находится в состоянии равновесия, то сумма всех сил, действующих на конструкцию, будет равна нулю.
Из этого условия равновесия и найдём искомую реакцию. Приложим некоторую силу R в месте, где закреплён наш стержень, при этом направить её можно в любую сторону, хоть влево, хоть вправо, главное, чтобы она была направлена горизонтально, так как у нас вся нагрузка, направлена так, то и реакция в заделке будет возникать исключительно — горизонтальная:

Чтобы составить уравнение равновесия, введём продольную ось – x, относительно неё будем составлять это уравнение, при этом силы, которые будут совпадать с положительным направлением оси x, в уравнении будем учитывать с «плюсом», а противоположно направленные с «минусом»:

Находим из этого уравнения реакцию в заделке:
А теперь, давай обсудим, что можем делать с этим теперь. В нашей конкретной задаче реакция может помочь проверить эпюру продольных сил. Если в первом уроке, считали стержень, строго справа налево, то теперь, зная численное значение реакции, можно рассчитать стержень и слева направо. Или как минимум увидеть, что левый участок эпюры, был построен верно.
Да, можно было вполне обойтись, без расчёта этой реакции конкретно в этом случае. Но, чаще всего, решение задач по сопромату начинается как раз с определения реакций, потому что без этого в большинстве случаев, невозможно определить внутренние усилия, а тем самым произвести какие-либо дальнейшие расчёты. Но с этим мы ещё многократно будем сталкиваться в следующих уроках, особенно в задачах на изгиб.
Построение эпюры нормальных напряжений
В отличие от продольных сил, нормальные напряжения уже зависят от формы бруса, а если точнее, то от площади его поперечных сечений.
Формула для определения нормальных напряжений выглядит так:

Таким образом, чтобы найти нормальное напряжение в любом сечении бруса, нужно: продольную силу в этом сечении разделить на площадь сечения.
Нормальные напряжения, как и продольные силы, изменяются по одному закону в пределах участков. Однако, так как форма бруса сказывается на распределении нормальных напряжений, здесь границами участков также служат места изменения геометрии бруса. Таким образом, для нашей расчетной схемы, нужно рассмотреть три участка и вычислить напряжения, соответственно, 3 раза:

Будем считать, что по условию задачи нам известны все параметры бруса, включая площади поперечных сечений: на первом участке площадь поперечного сечения A1=2 см2, а на втором и третьем A2 = A3 = 4 см2.

Вычисляем напряжения на каждом участке:

По полученным значениям строим эпюру нормальных напряжений:

По полученной эпюре нормальных напряжений, можно определить те поперечные сечения, в которых напряжения будут максимальными (все сечения на участке 1), что полезно при проведении прочностного расчёта.
Построение эпюры осевых перемещений поперечных сечений
Под действием внешней нагрузки поперечные сечения бруса перемещаются вдоль продольной оси. Под нагрузкой брус может как удлиниться, так и укоротиться. И в этом разделе будем учиться определять эти перемещения.
Для начала подготовимся к расчету и расставим точки в характерных сечениях. Чтобы потом к ним привязываться по ходу решения:

Если для первых двух эпюр, расчет начинался справа налево, от свободного конца. То здесь нам нужно начать считать с закрепленного конца, с жесткой заделки и так как сечение A, закреплено жестко, то никакие перемещения этого сечения невозможны, поэтому сразу можем записать:
Эпюра перемещений так же, как и остальные эпюры, меняется по одному закону, в пределах участков. Поэтому, чтобы построить эпюру, достаточно определить эти перемещения в характерных точках.
Перемещение точки B будет складываться из перемещения предыдущего расчетного сечения:
А также удлинения (или укорочения) участка между расчетными сечениями:
В свою очередь, удлинение (или укорочение) любого участка, можно определить по следующей формуле:

Поэтому формулу, для нахождения перемещения сечения B, можно записать и в другом виде:

Подставив все численные значения, найдем искомое перемещение:

Откладываем полученное значение на эпюре:

Также важно отметить, что при вычислении удлинения или укорочения участка (Δl), фактически площадь эпюры продольных сил (ω) делится на жесткость при растяжении или сжатии (EA).


Это свойство нам еще пригодится, когда будем рассматривать более сложную задачу.
Для точек C и D перемещения находятся аналогичным способом, так же как и для точки B, поэтому подробно комментировать не буду, приведу решение.
Точка C

Точка D

Откладываем полученные значения на эпюре:

По полученной эпюре, можно увидеть — в какую сторону и насколько переместится любое поперечное сечение стержня. Наиболее интересной характеристикой здесь является перемещение сечения D, то есть перемещение свободного конца бруса или фактическое удлинение. Как видим, сечение D переместится вправо на величину WD (т. к. значение WD — положительное). То есть, под действием всей нагрузки брус удлинится на 0.575 мм.
Учёт распределённой нагрузки
А теперь предлагаю рассмотреть немного измененную задачу. Приложим к нашему брусу дополнительно распределенную нагрузку q с интенсивностью равной 2 кН/м. После чего рассчитаем и построим все те же эпюры: продольных сил, нормальных напряжений и перемещений.

Чтобы учесть распределенную нагрузку, необходимо интенсивность нагрузки (q) умножить на длину участка, на котором действует нагрузка. В чистом виде, только от распределенной нагрузки, эпюра продольных сил будет треугольная.

Расчет продольных сил
На первом участке, сила по-прежнему растягивает стержень, записываем ее в уравнение с «плюсом», а распределенная нагрузка сжимает, соответственно, ее учитываем с «минусом»:
Найдем значения продольной силы на границах первого участка:

Откладываем рассчитанные значения:

На втором участке, распределенная нагрузка будет действовать точно так же, как и сосредоточенная сила:
Рассчитываем продольную силу на третьем участке:
Строим окончательную эпюру продольных сил:

Расчет нормальных напряжений
Нормальные напряжения рассчитываются точно так же, как и для первой задачи, единственное отличие только в том, что на первом участке необходимо рассчитать напряжения два раза — на границах участка:

По полученным значениям строим эпюру нормальных напряжений:

Расчет перемещений
Для точек A, B и С перемещения рассчитываются аналогично, как в первой задаче:


Строим эпюру перемещений на втором и третьем участке:

Чтобы рассчитать удлинение на первом участке, нужно вычислить площадь эпюры продольных сил на этом участке и разделить на жесткость (EA):


Так как на этом участке, эпюра состоит из двух одинаковых прямоугольных треугольников, но по разные стороны от нулевой линии, с учетом знаков, ожидаемо, получим, что перемещение точки D, будет равно перемещению точки C.



Однако, необходимо учесть еще одну особенность. На участках, где действуют распределенные нагрузки, эпюры перемещений изменяются не по линейному закону, а по квадратичному.
То есть на участке с распределенной нагрузкой, эпюра перемещений всегда будет иметь либо выпуклость, либо вогнутость:

Чтобы понять, как же будет выглядеть эпюра перемещений, на участке с распределённой нагрузкой, нужно проанализировать эпюру продольных сил.
Как видим, начиная от точки C и до пересечения нулевой линии, эпюра продольных сил – отрицательна, а это значит, что эпюра перемещений, на этом отрезке, также должна убывать, как показано зелёной пунктирной линией. Поэтому изображаем эпюру перемещений следующим образом:

Но чтобы окончательно убедиться в верности наших рассуждений, можно также определить экстремум на эпюре перемещений (там, где эпюра достигает своего максимального значения). Или в той точке, где эпюра продольных сил пересекает нулевую линию:


Отмечаем найденное значение на эпюре перемещений:

В этом разделе рассматриваются расчёты на прочность и жёсткость при растяжении и сжатии. Растяжение и сжатие возникает:
–в опорных стержнях, поддерживающих какие либо конструкции (например, сооружения, плоские и пространственные рамы), – в целом эти системы называют стержневыми;
–в стержнях ферм (напомним, что фермы − это системы из прямолинейных стержней, соединённых по концам шарнирами);
–в элементах конструкций, имеющих вид прямого бруса постоянного или переменного сечения и нагруженных продольной нагрузкой.
Например, как прямой брус при действии растягивающей силы рассматривают болты и винты, применяемые в механических соединениях, трос подъёмного механизма; как прямой брус изображают следующие элементы, воспринимающих продольную нагрузку: колонны зданий и оборудования, фабричные трубы, столбчатые фундаменты, которые сжаты собственном весом и верхней нагрузкой.
При составлении схем расчёта при растяжении и сжатии учитываются геометрия всей системы, вид внешнего воздействия и способ присоединения (или опирания). Если присоединение фактически препятствует смещению и повороту, то на схеме изображается так называемая жёсткая заделка. Если опора не позволяет линейного перемещения, а поворот частей системы относительно друг друга происходит, то такое соединение называют шарнирным и на расчётной схеме изображают шарнир.
По количеству имеющихся опор схемы для расчёта могут быть как статически определимыми (количество опорных связей равно количеству уравнений равновесия), так и статически неопределимыми (количество опорных связей превышает количество уравнений равновесия). Ввиду этого в данном пособии рассматривается решение следующих задач, которые даны в курсовой работе и расчётно-графических заданиях по сопротивлению материалов.
Задача 1. Подбор размеров сечения стержней стержневой системы.
Задача 2. Подбор размеров сечения стержней фермы. Задача 3. Проектный расчёт ступенчатого бруса.
Задача 4. Проектный расчёт ступенчатого статически неопределимого бруса.
7
Задача 5. Проектный расчёт стержневой статически неопределимой системы.
Задача 6. Проверочный расчёт ступенчатого бруса.
Задача 7. Проверочный расчёт ступенчатого статически неопределимого бруса.
В каждой из названных задач необходимо выполнить расчёт на прочность, в ходе которого всегда требуется знать значение внутренней продольной силы N, т. к. в случае растяжения и сжатия в поперечных сечениях бруса возникают только продольные силы, которые и позволяют оценить сопротивление бруса внешним воздействиям.
Известно, что в общем случае нагружения в поперечном сечении бруса могут возникать шесть разных внутренних усилий, но при решении задач изображают и вычисляют только те усилия, которые не равны 0. Так, при растяжении и сжатии по виду внешних сил видно, что в сечении возникает лишь продольная сила N.
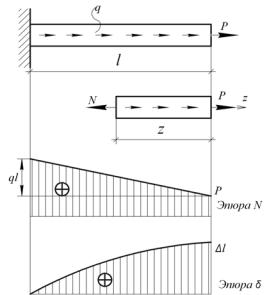
Выполним вычисление продольной силы N на примере бруса с нагрузкой общего вида: в начальном сечении бруса покажем сосредоточенную силу Р и по всей длине распределённую нагрузку интенсивности q (рис. 1.1, а). Введём правило знаков нагрузки: принимаем за положительное то направления, которое вызывает растяжение.
а
б
в
г
Рис. 1.1
Значения продольной силы вычисляют методом сечений, выполняя последовательно правило РОЗУ: Разрезать, Отбросить, Заменить, Уравновесить. Выполним разрез бруса на расстоянии z от свободного края (это бу-
8
дет текущее сечение) и изобразим правую часть (рис. 1.1, б). В текущем сечении поставим силу N. Если изобразить силу N от сечения, то она растягивает отсечённую часть бруса. Такое направление продольной силы принято считать положительным. Заметим, что, поставив силу N в текущем сечении, мы произвели замену воздействия отброшенной части бруса на оставленную. Составим уравнение равновесия. Как известно, для пространственного тела имеем шесть уравнений равновесия, но при растяжении-сжатии из шести уравнений равновесия только одно не превращается в тождество 0 = 0, − это сумма проекций всех сил на продольную ось бруса:
|
Σ пр z = 0. |
(1.1) |
|
В нашем примере в это уравнение войдут внешние силы P и qz и |
|
|
внутренняя продольная сила N, тогда уравнение принмет |
вид |
|
N qz P 0, отсюда получим формулу продольной силы |
|
|
N qz P . |
(1.2) |
Как видно, продольная сила N в сечении равна алгебраической сумме проекций на ось z всех внешних сил, действующих по одну сторону от рассматриваемого сечения. Получается закономерность: положительная внешняя нагрузка создаёт положительную продольную силу.
Принято изображать график изменения N вдоль оси, который называют эпюрой N. Этот график удобен, т. к. наглядно показывает изменение силы вдоль бруса и определяет опасное сечение: опасным является сечение, в котором продольная сила принимает максимальное значение (определяется максимальная растягивающая и максимальная сжимающая силы). Эти значения являются расчётными значениями силы и необходимы для составления условия прочности.
Для построения эпюры N вычислим значения силы в начале бруса (при z = 0) и в конце (при z = l). Получим граничные значения продольной силы: N (0) P, N (l) ql P. Отложив эти значения от базисной (нуле-
вой) линии, проведённой под брусом, соединим значения согласно (1.2) наклонной прямой и получим эпюру N. При положительных значениях нагрузки, показанной на чертеже бруса, она выглядит нарастающей от свободного края по линейному закону (рис. 1.1, в). Реальная нагрузка вносит свои коррективы. С одной стороны, подставляя значения реальной нагрузки в формулу (1.2), можно получить функцию продольной силы и построить эпюру N для любого грузового участка расматриваемого бруса. С другой – формула (1.2) позволяет проследить закономерности функции N, связанные с видом и направлением внешней нагрузки:
на участке, где интенсивность распределённой нагрузки q 0, продольная N = const , и на эпюре N – прямая, параллельная оси;
9
на участке с распределённой нагрузкой, где q ≠ 0, продольная N изменяется линейно, и на эпюре N – наклонная прямая, причём при q > 0 продольная сила растёт, при q < 0 продольная сила уменьшается.
Заметим следующие методические приёмы при нахождении силы N:
1.Силу N в сечении лучше предполагать положительной (т. е. направленной от сечения). Это удобно, т. к. получив её значение, автоматически указывается знак «+» при растяжении и знак «–» при сжатии, что особенно важно при расчёте бруса из материала, не одинаково работающего на растяжение и сжатие.
2.Определение продольной силы для бруса с заделкой удобно выполнять, рассматривая отсечённую часть со стороны свободного края, т. к. при этом не обязательно определение опорных реакций.
Расчёт элементов деталей машин и механизмов ведётся в пределах упругих деформаций, поэтому используют условие прочности по допус-
. Согласно этому усло-
вию напряжения σ не должны превышать допускаемого напряжения .
При растяжении-сжатии нормальные напряжения в поперечном сечении бруса σ равномерно распределены по площади (рис. 1.2) и определяются как отношение продольной силы к площади сечения:
|
N |
. |
(1.3) |
|
|
F |
В рассматриваемых задачах имеются, во-первых, стержни, в которых площадь сечения F и продольная сила вдоль оси постоянны, и, во-вторых, ступенчатый брус, имеющий несколько грузовых участков с разной площадью сечения F и различным характером нагрузки. Для первых стержней условие прочности по допускаемым напряжениям записываем как
а для ступенчатого бруса условие прочности принимает вид
|
N |
σ . |
||
|
σmax |
(1.5) |
||
|
F max |
Нужно помнить, что для пластичных материалов (например, для малоуглеродистых низколегированных сталей) имеем одинаковые допускае-
мые напряжения на растяжение и сжатие, т. е. σр = σ c = σ , а для хруп-
ких материалов (например, для чугуна) допускаемые напряжения на рас-
10
|
тяжение |
σ |
и на сжатие |
σ |
c |
различны. Поэтому для пластичных мате- |
||
|
р |
риалов составляем одно условие прочности, а для хрупких − два условия. По условию прочности возможно выполнение трёх видов расчёта на
прочность:
проектный расчёт (это определение размеров сечения);
проверочный расчёт (вычисление напряжений и проверка прочности);
определение несущей способности (нахождение величины на-
грузки).
В задачах рассмотрены два первых вида расчёта.
При работе реальных систем длина стержня или его части изменяется, что вносит свои особенности в обслуживание и сохранение работоспособности всей системы, поэтому в задачах предусмотрено вычисление деформаций и проверка жёсткости. Величина изменения длины стержня
|
(рис. 1.2, а), называемая абсолютной деформацией |
l, вычисляется как |
|||
|
l l |
N |
dz , |
(1.6) |
|
|
EF |
||||
|
0 |
где E – модуль продольной упругости (или модуль Юнга), для стали и чугуна Е = 2 · 105 МПа, для алюминиевых сплавов Е = 0,65 · 105 МПа; вели-
чина EF – жёсткость сечения при растяжении и сжатии.
За счёт деформации стержня происходит поступательное перемещение δ поперечных сечений стержня в продольном направлении. Поясним вычисление перемещений δ на нашем примере (рис. 1.1, г). Перемещение заделки δА равно 0, а свободный край бруса переместился на величину деформации всего бруса, которую найдём по (1.6):
|
l |
N |
l |
P qz dz |
1 |
z |
2 |
l |
1 |
q l |
2 |
||||||||
|
δ= A l |
dz |
Pz q |
Pl |
. |
||||||||||||||
|
EF |
2 |
|||||||||||||||||
|
0 |
0 EF |
EF |
0 |
EF |
2 |
|||||||||||||
Выражение, полученное после интегрирования, показывает, что имеем функцию 2-го порядка по отношению к переменной z (это результат действия распределённой нагрузки), значит, величина перемещения текущего сечения, задаваемого абсциссой z, изменяется вдоль бруса по квадратичной зависимости от z, – по квадратичной параболе.
При расчёте ступенчатого бруса для вычисления перемещений отдельных (так называемых характерных) сечений необходимо знать абсолютные деформации грузовых участков бруса, определяемые формулой (1.6). При этом перемещение i-го сечения будет равно перемещению (i-1)-го плюс деформация li i-го участка:
11
Используя полученные значения перемещений, строят эпюру δ, которая наглядно показывает изменение продольных перемещений вдоль бруса и позволяет выбрать его наибольшее значение δmax. Для бруса, изображённого на рис. 1.1, эпюра δ будет криволинейной, для которой нужно правильно выбрать форму кривой. Для определения угла наклона касательной к кривой перемещений возьмём производную от функции перемещений (1.7), с учётом (1.6) получим
|
d (δi-1 |
l |
N |
dz) |
||||||||||||
|
dδ |
d (δ |
l ) |
EF |
N |
|||||||||||
|
tgα |
i |
. |
(1.8) |
||||||||||||
|
i-1 |
i |
0 |
|||||||||||||
|
dz |
dz |
||||||||||||||
|
dz |
EF |
Как видно, угол наклона касательной к кривой перемещений повторяет закон изменения силы N, поэтому эпюра N всегда позволяет определить наклон кривой δ. Так, в рассматриваемом примере сила N растёт от свободного края к заделке, поэтому угол наклона касательной увеличивается к заделке, и выпуклость обращена вверх (рис. 1.1, г).
Нужно заметить, что согласно (1.8) функция перемещений δ(z) на порядок выше функции N(z):
на участке бруса, где N = const и эпюра N – прямая, параллельная оси, на эпюре перемещений δ будет наклонная прямая;
на участке, где на эпюре N – наклонная прямая, на эпюре переме-
щений δ будет кривая 2-го порядка (парабола), изогнутость которой и определяется по значениям (1.8).
Для обеспечения нормальной работы конструкции необходимо, чтобы значение δmax не превышало допускаемого перемещения и чтобы выполнялось условие жёсткости
Это условие позволяет выполнять те же три вида расчётов, что и условие прочности. Поэтому, когда оно для рассматриваемого элемента не соблюдается, по нему определяют требуемые величины.
Для правильного контроля работы конструкций надо знать, какие напряжения возникают не только в осевом направлении, но и на любом наклонном к оси. Если стержень разрезать двумя поскостями (рис. 1.2, а): плоскостью 1–1, перпендикулярной оси, и плоскостью 2–2, наклонённой к поперечному сечению под углом α, далее выделить полученную часть стержня (рис. 1.2, б) и рассмотреть её равновесие по уравнению (1.1), − то получим в наклонном сечении напряжения pα , параллельные σ и равные
σ cosα. Разложим вектор напряжения pα на нормаль и касательную к на-
12
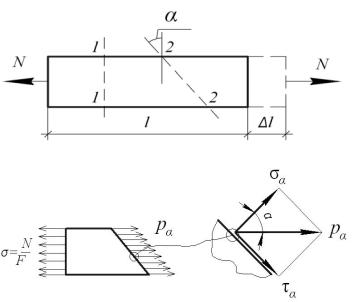
клонному сечению и получим, что при растяжении-сжатии в наклонных сечениях возникают и нормальные σα , и касательные τ напряжения
(см. рис. 1.2, б):
|
σα σ cos2 α; |
τα= |
σ |
sin2α. |
(1.10) |
|
2 |
Формулы (1.10) показывают, что наибольшие нормальные напряжения возникают в поперечных сечениях, а наибольшие касательные – на площадках под углом α = 45º, на которых касательные и нормальные напряжения одинаковы по величине:
τα 45 τmax σ2 ; σα 45 σ2 .
а
б
Рис. 1.2
Этот факт позволяет обьяснить реальное сопротивление растяжению и сжатию разных материалов. Рассмотрим широко распространённые конструкционные материалы: сталь и чугун. Сталь как пластичный материал при сжатии деформируется за счёт сдвига и наибольший сдвиг получает от наибольших касательных напряжений под углом 45 . Когда этими напряжениями достигается величина предела текучести стали при сдвиге τт (т. е. при α= 45 = Т ), наблюдается интенсивный сдвиг по этому направле-
нию, а образец принимает бочкообразную форму (рис. 1.3, а). Известно, что предел текучести стали при сдвиге τт составляет приблизительно 0,6 от предела текучести при растяжении-сжатии σт. Отсюда понятно, что
13
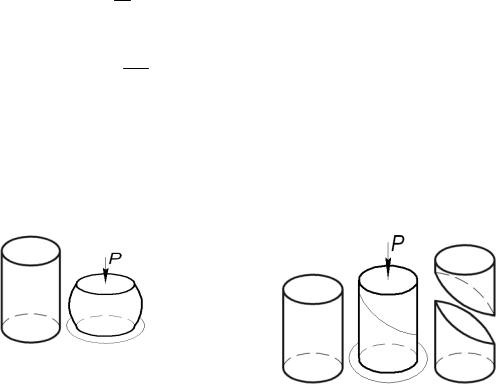
при τα = τт образец не разрушается ни от сжимающих напряжений в поперечном сечении FP , которые меньше предела текучести σT (т. е. не раскалывается), ни от растягивающих напряжений в наклонных сечениях–45 cos2 ( 45 ) 2PF , которые больше предела текучести σT (т. е. не
разрывается), а получает большую пластичную деформацию сдвига, приводящую к бочкообразной форме. При дальнейшем увеличении напряжений деформация сдвига нарастает с большой скоростью, образец сплющивается, − это говорит о том, что допускать предел текучести для стальных конструкций опасно.
|
Стальной образец до |
Чугунный образец до испытания и после |
|
и после сжатия |
разрушения от сжимающей силы |
|
а |
б |
|
Рис. 1.3 |
При сжатии чугунного образца (рис. 1.3, б) наблюдается хрупкий скол по плоскости под углом α 45 к оси. Объяснить такое разрушение можно тем, что чугун хорошо сопротивляется сжатию и слабо – растяжению. Образец разрывается от действующих под углом α = 45 к оси бруса растягивающих напряжений, достигших предела прочности на растяже-
|
ние |
σвр : σα 45 |
σ |
P |
σвр. Линия разрыва перпендикулярна направле- |
||||
|
2 |
2F |
|||||||
нию этих напряжений и наклонена под –45º к оси бруса. Для закрепления знаний о напряжениях при расчёте ступенчатого бруса можно предусмотреть вычисление напряжений под углом α = 45 к оси бруса по (1.10).
14

Задача 1 Подбор размеров сечения стержней стержневой системы
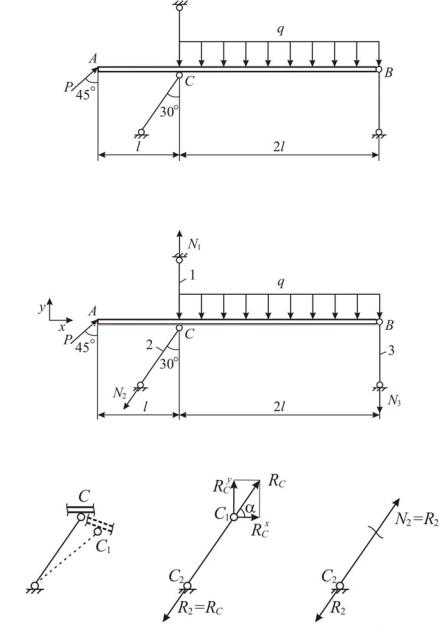
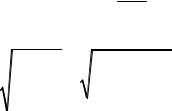
В плоской стержневой системе (рис. 1.4, а) абсолютно жёсткий брус АB имеет три опорных стержня и несёт нагрузку известной величины. Ис-
ходные значения: l 2 м; q 15 кН/м; P 2 ql ; стержни 1, 2 круглого сечения, стержень 3 – квадратного.
Требуется
1.С помощью уравнений равновесия определить усилия в опорных стержнях.
2.Подобрать площади поперечного сечения стержней из условия прочности по допускаемым напряжениям, если допускаемое напряжение
на сжатие σс 120 МПа, на растяжение σр = 40 МПа. Назначить размеры сечений, принимая два стержня круглого и один квадратного сечений.
Решение
1. Определение продольных усилий в опорных стержнях
Опорные стержни 1, 2, 3 имеют по концам шарниры (рис. 1.4, б). При действии внешних сил на жёсткий брус АВ эти стержни деформируются (изменяют длину) и за счёт деформаций шарниры B и C перемещаются: на рис. 1.4, в для шарнира С показано новое положение С1 , при котором
соединяемые элементы (брус АВ и стержень 2) повернулись друг относительно друга, и край С получил горизонтальное и вертикальное перемещения. Эти перемещение края С произошли от горизонтального и верти-
кального воздействия со стороны бруса АB . Обозначим их RСx и RСy , по-
кажем эти усилия на рис. 1.4, г. Законченный поворот стержня 2 говорит о том, что для него соблюдается условие равновесия момС2 0 :
|
Ry cosα СС |
– Rx |
sinα СС |
2 |
0. |
|||||||
|
С |
1 2 |
С |
1 |
||||||||
|
Здесь равенство |
нулю возможно, если |
проекции R y cos и |
|||||||||
|
С |
|||||||||||
|
Rx |
sin равны нулю, т. е. полная реакция |
C |
Cx |
Cy направлена вдоль |
|||||||
|
R |
R |
R |
|||||||||
|
C |
|||||||||||
|
стержня. Следовательно, в сечении C2 |
возникает реакция R2 = RC , направ- |
ленная в противоположную сторону вектора RC .
15
а
б
Очевидно, для стержня, имеющего по концам шарниры, будут всегда верны эти рассуждения; используя их, будем сразу направлять реакции вдоль такого стержня.
Замечание 1: стержень, имеющий по концам шарниры, может быть только либо растянут, либо сжат.
16

Для подбора размеров сечений небходимо знать, какое внутреннее усилие возникает в каждом из стержней 1, 2, 3. Внутренние усилия определяют методом сечений. Например, разрежем стержень 2 в каком-либо месте и рассмотрим одну, пусть, нижнюю часть (рис. 1.4, д). Она нагружена реакцией R2 (это внешняя для стержня нагрузка) и силой N2 (это внут-
реннее для стержня усилие). Равновесие возможно, если N2 R2
(рис. 1.4, д). Ввиду этого можно обозначать реакции опорных стержней как N1 , N2 , N3 (рис. 1.4, б) и направлять их вдоль стержней.
Заметим, что для условия прочности важно знать направление продольной силы, которая оценивается знаком: если сила N направлена от проведённого сечения и растягивает стержень, то она считается положительной, если сжимает, то она направлена к сечению и в её цифровом значении ставится знак «–».
Чтобы автоматически при расчёте получить правильный знак N , поставим для всех стержней направление усилий N1 , N2 , N3 положитель-
ным, т. е. растягивающим.
Усилия N1 , N2 , N3 должны удовлетворять условиям равновесия бруса АB . Брус нагружен внешней нагрузкой P и q и усилиями N1 , N2 , N3 , которые представляют в совокупности плоскую систему сил, поэтому для бруса АB имеем три уравнения равновесия:
пр x 0;пр y 0;
момC 0.
Запишем эти уравнения:
P sin 45 N1 sin 30 0;
P cos 45 N1 cos30 N2 N3 q 2l 0;
P cos 45 l N2 2l q 2l l 0.
Из третьего уравнения получим
N2 21l ( Pcos45 l 2 ql2 ) 21l ( 2 ql cos45 l 2 ql 2 )
ql(cos 45 1) 1,707 ql 1,707 15 103 2 51 210 Н 51,21 кН.
Продольное усилие N2 отрицательно, значит, стержень 2 сжат. Из первого уравнения получим
|
N1 |
Psin 45 |
2 ql sin 45 |
2,828 ql 2,828 15 103 2 84,84 кН. |
|
|
sin 30 |
sin 30 |
17

Продольное усилие N1 положительно, значит, стержень 1 растянут. Из второго уравнения получим
N3 Pcos45 N1 cos30 N2 2 ql 2 ql cos45
2,828 ql cos30 ( 1,707 ql) 2 ql 1,328 ql 1,328 15 103 2 39,84 кН.
Продольное усилие N3 положительно, значит, стержень 3 растянут.
Для проверки правильности найденных усилий в опорных стержнях составим уравнение равновесия мом A 0:
N1 cos30 l N2 3l q 2l 2l N3l 0 ;
2,828 ql cos30 ( 1,707 ql) 3 4 ql 1,328 ql 0 ;
6,449 6,449 0 ,
значит, существует тождество 0 0 которое говорит, что проверка сошлась, следовательно, усилия в стержнях найдены верно.
2. Подбор размеров поперечного сечения стержней
Подбор размеров сечения стержней выполняется по условию прочности по допускаемым напряжениям при растяжении-сжатии (1.4), согласно которому для каждого стержня
σi Ni σ ,
Fi
где σi – нормальное напряжение; σ – допускаемое нормальное напряже-
ние, причём если стержень растянут, то принимаем σ = σр , если сжат,
то σ = σс ; Ni – продольное усилие в стержне; F – поперечное сечение
стержня.
Для стержня 1 круглого сечения площадь поперечного сечения
F 4d 2 0,25 d 2,
где d – диаметр стержня.
Стержень 1 растянут, поэтому условие прочности (1.11) для него принимает вид
σ1 N1 σр .
F1
18
Подставляя выражение площади стержня 1 F1 0, 25 πd 2 , получим
|
N1 |
|||||||
|
0,25 πd 2 |
|||||||
|
σр . |
|||||||
|
Отсюда |
|||||||
|
d |
N |
84,84 103 |
0,05197 м 5,197 cм. |
||||
|
0,25 π σ |
0,25 40 106 |
||||||
|
1 |
|||||||
|
р |
Принимаем в соответствии со знаком «больше либо равно» d1 3 cм.
Замечание 2: полученное из условия прочности значение размеров сечения назначается в бóльшую сторону.
Составим условие прочности для стержня 2. Стержень 2 сжат, тогда по условию (1.11)
|
σ2 |
N2 |
σс . |
||||
|
F |
||||||
|
2 |
Замечание 3: для сжатого стержня в условие прочности ставим модуль продольной силы.
Подставляя площадь круглого сечения F2 0,25 πd 2 , получим
|
N2 |
σс . |
||||
|
0,25 πd 2 |
|||||
|
Отсюда |
|
d |
N2 |
51,21 103 |
0,02331м 2,331cм. |
||||
|
0,25 π |
σс |
0,25 π 120 106 |
Принимаем d2 2,4 cм.
Для стержня 3 квадратного сечения площадь
F3 a2 ,
где a – сторона квадрата.
Стержень 3 растянут, условие прочности (1.11) для него принимает
вид
σ3 N3 σр .
F3
19
Подставляя выражение площади квадратного сечения, получим
Na32 р .
Отсюда
|
a |
N3 |
39,84 103 |
0,03156 м 3,156 cм. |
||||||
|
40 106 |
|||||||||
|
σр |
Принимаем a 3,2 cм.
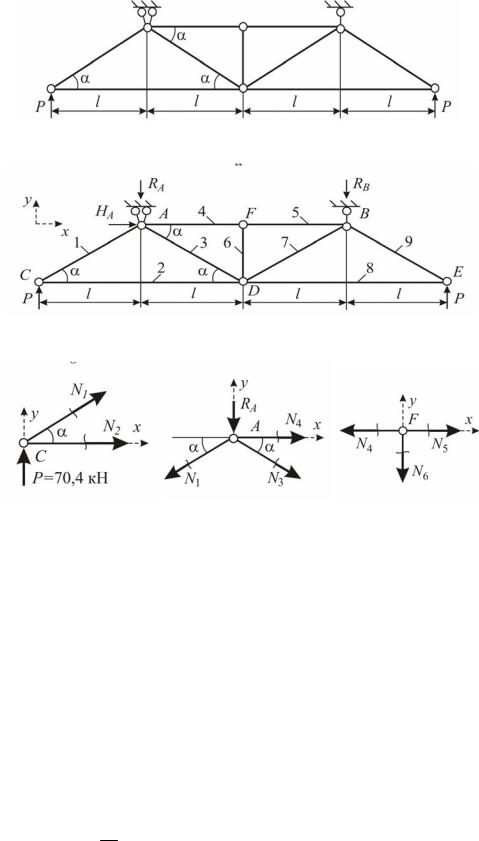
Задача 2 Подбор размеров сечения стержней фермы
Для плоской фермы (рис. 1.5, а) задана нагрузка. Исходные значе-
ния: l 0,8 м; q 40 кН/м; P 2,2 ql ; α 45 .
Требуется
1.С помощью уравнений равновесия определить опорные реакции.
2.Используяметодвырезанияузлов, вычислитьусилиявстержняхфермы.
3.Подобрать размеры поперечного сечения стержней из условия
прочности по допускаемым напряжениям, если σ 200 МПа. Сечение
сжатых стержней принять в форме кольца с соотношением внутреннего и внешнего диаметров 0,5, и сечением растянутых стержней в виде швеллера.
Решение
1. Определение опорных реакций
Обозначим реакции, возникающие в опорах A и B . Опора B шар- нирно-подвижная, имеем один вертикальный опорный стержень, вдоль которого возникает одна вертикальная реакция RB (см. замечание 1)
(рис. 1.5, б). Опора A шарнирно-неподвижная, она препятствует смещению узла A по вертикали и горизонтали, поэтому в ней в общем случае возникает две реакции: горизонтальная H A и вертикальная RA , но по-
скольку в горизонтальном направлении нет других сил, то из уравненияпр x 0 следует, что H A 0 .
20
а
б
Ферма нагружена системой параллельных сил P , RA и RB . Составим два уравнения равновесия:
мом A 0;
мом B 0.
Запишем эти уравнения:
|
R |
2l – P 3l P l 0; |
(1.12) |
|
|
B |
(1.13) |
||
|
–RA 2l P 3l P l 0. |
Из (1.12) RB 21l P 3l P l P 2,2 ql 2,2 40 0,8 70,4 кН.
21

Из (1.13) RA 21l P 3l P l P 2,2 ql 2,2 40 0,8 70,4 кН.
Проверку найденных рекций выполним по неиспользованному уравнению, которое при правильном вычислении реакций удовлетворяется тождественно, пр y 0 :
RA RB P P 0;
2,2 ql 2,2 ql 2,2 ql 2,2 ql 0 ; 4,4 ql 4,4 ql 0 ; 0 0 ,
значит, реакции найдены верно.
Равенство RA RB есть следствие симметрии фермы, поэтому можно сформулировать следующее замечание.
Замечание 4: в симметричной схеме при симметричной нагрузке реакции равны друг другу, а величина их составляет половину нагрузки.
2. Определение усилий в стержнях фермы
Обозначим узлы и пронумеруем стержни (рис. 1.5, б). В стержнях ферм, которые имеют по концам шарниры, возникают только продольные силы (см. замечание 1). Их значение определим методом вырезания узлов, который основан на методе сечений. По этому методу последовательно вырезаем каждый узел фермы и рассматриваем его равновесие. В данной ферме в силу её симметрии необходимо и достаточно выделить три узла: узлы A , C , F .
Первым вырезаем узел C (рис. 1.5, в), в котором сходятся два стержня: 1 и 2. Продольные усилия в стержнях N1 и N2 направляем от сечения,
предполагая растяжение. Для этого, как и для каждого узла, имеем сходящуюся систему сил, поэтому составляем два уравнения равновесия, из которых и найдём неизвестные усилия:
|
пр x 0; |
(1.14) |
||||||||
|
пр y 0. |
|||||||||
|
Запишем эти уравнения для узла C : |
|||||||||
|
N |
2 |
N cosα 0; |
N2 N1 cos 45 0; |
||||||
|
1 |
или |
||||||||
|
P N |
sin α 0, |
N1 |
sin 45 0. |
||||||
|
70,4 |
|||||||||
|
1 |
Из полученных уравнений вычислим усилия N1 и N2 :
22

N1 sin7045,4 99,56 кН;
N2 N1 cos45 99,56 cos45 70,4 кН.
Продольное усилие N1 отрицательно, значит, стержень 1 сжат. Продольное усилие N2 положительно, поэтому стержень 2 растянут.
Следующим нужно рассматривать узел, в котором неизвестны два продольных усилия; в нашем примере вырезаем узел A (рис. 1.5, г), в котором неизвестны усилия в стержнях 3 и 4. Ставим усилия в стержнях N1 ,
N3 , N4 и реакцию RA . Составляем уравнения равновесия узла A по (1.14):
N4 N3 cos N1 cos 0;RA N3 sin N1 sin 0.
Подставив уже найденное значение N1 , получим систему двух уравнений относительно неизвестных N3 и N4 :
N4 N3 cos45 99,56 cos45 0;70,4 N3 sin 45 99,56 sin 45 0.
Отсюда
N3 sin145 70,4 99,56 sin 45 0 ;
N4 99,56 cos45 N3 cos 99,56 cos45 0 70,4 кН.
Стержень 3 не растягивается и не сжимается, поскольку продольное усилие в нём равно нулю. Так как продольное усилие N4 отрицательно, то
стержень 4 сжат.
Сдедующим вырезаем узел F (рис. 1.5, д), для которого уравнения
|
равновесия по (1.14) будут |
||
|
N4 N5 0; |
или |
70,4 N5 0; |
|
N6 0, |
N6 0. |
|
|
Получаем N6 0 и N5 |
N4 70,4 кН. Стержень 6 не деформирует- |
ся, поскольку продольное усилие в нём равно нулю. Усилие N5 отрица-
тельно, это означает, что стержень 5 сжат.
Поскольку конструкция симметричная, то достаточно рассмотреть лишь одну её половину и можно записать внутренние усилия в симметричных стержнях второй половины, т. е. усилия попарно равны:
23
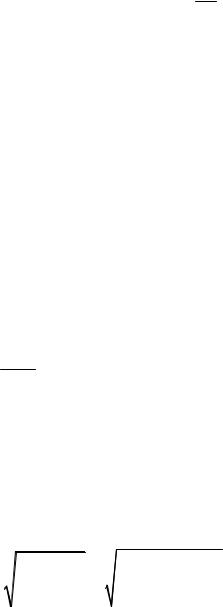
N7 N3 N6 0 кН; N8 N2 70,4 кН;
N5 N4 70,4 кН; N9 N1 99,56 кН.
3. Подбор размеров сечения стержней
Размеры поперечного сечения стержней подбираем из условия прочности по допускаемым напряжениям, которое при растяжении-сжатии по (1.4) имеет вид
σi Ni σ ,
Fi
где σi – нормальное напряжение в стержне; σ – допускаемые нормальное напряжение, здесь при растяжении и сжатии они одинаковы; Ni – продольное усилие в стержне; Fi – поперечное сечение стержня.
Для растянутых стержней нужно выбирать номер швеллера. Если нет
дополнительных условий, считаем все растянутые стержни одинакового
сечения. Максимальные растягивающие усилия Nmaxр 70,4 кН, тогда из условия прочности требуемая площадь сечения растянутых стержней
|
F |
Nmaxр |
70,4 103 |
4 |
2 |
2 |
||||
|
200 106 |
3,52 10 |
м |
3,52 см |
. |
|||||
|
σ |
По таблице ГОСТ 8240–93 (см. табл. 5 прил. 1) выбираем швеллер № 5 с площадью F 6,16 см2 для стержней 2 и 8.
Для сжатых стержней выбираем кольцевое сечение, для которого площадь F π4d 2 1 c2 . Считая все сжатые стержни одинаковой площа-
ди и взяв максимальное сжимающее усилие Nmaxс 99,56 кН, найдём тре-
буемую площадь сечения:
|
F |
N maxс |
99,56 103 |
4,978 10 |
4 |
м |
2 |
4,978 см |
2 |
. |
|||||
|
σ |
200 106 |
|||||||||||||
|
Тогда диаметр поперечного сечения сжатых стержней |
||||||||||||||
|
d |
F 4 |
4,978 10 4 |
4 |
2,91 10 |
2 |
м = 2,91cм. |
||||||||
|
2 |
2 |
|||||||||||||
|
π 1 c |
π 1 0,5 |
|||||||||||||
Принимаем диаметр d 3 cм для стержней 1, 4, 5, 9.
Стержни, в которых N 0 , можно взять также круглого сечения, поэтому для стержней 3, 6, 7 принимаем диаметр d 3 cм.
24
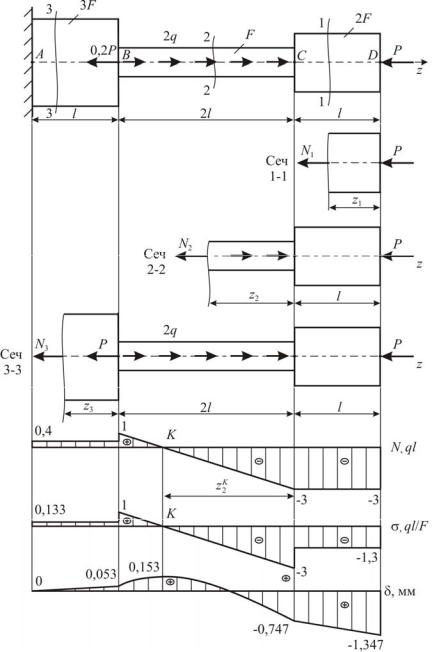
Задача 3 Проектный расчёт ступенчатого бруса
Для стального ступенчатого бруса (рис. 1.6, а) задана конфигурация и известна внешняя нагрузка. Исходные значения: l 1,2 м; q 20 кН/м;
P 3 ql .
Требуется
1.Построить эпюру продольных сил N .
2.Составить выражения для нормальных напряжений σ по всем участкам бруса, используя указанные на схеме бруса значения площадей сечения через неизвестную величину F .
3.Установить σmax , составить условие прочности бруса по допускае-
мым напряжениям. Найти из этого условия требуемое значение F приσ 200 МПа и назначить площади всех участков бруса, соблюдая указан-
ное соотношение между ними.
4. Построить эпюры нормальных напряжений и продольных перемещений δ, считая модуль упругости E 2 105 МПа. Указать δmax и проверить жёсткость при допускаемом продольном перемещении δ = 0,5 мм. Ес-
ли условие жёсткости не удовлетворяется, назначить новыеплощади сечений. 5. Для опасного сечения бруса вычислить касательные τα и нормаль-
ные σα напряжения в наклонной площадке, проведённой под углом
α= 45° к оси бруса.
6.Определить силу P0 , которую нужно приложить к свободному
торцу бруса, чтобы вернуть его в первоначальное положение.
Решение
1. Построим эпюру продольных сил N
Вычислим значения продольных сил методом сечений. Данный брус состоит из 3 участков. Будем рассматривать отсечённые участки для каждого из них, начиная со свободного конца (рис. 1.6, б, в, г). При этом продольную силу в сечении, которая является внутренним усилием, всегда изображаем положительной, т. е. растягивающей рассматриваемый участок.
Уравнение равновесия для отсечённой части каждого участка при растяжении-сжатии представляет собой равенство нулю суммы проекций всех сил на продольную ось (1.1), т. е. пр z 0 .
25
Записывая это уравнение последовательно для всех участков, полу-
|
чим продольные силы для каждого участка: |
|||
|
N1 P 3 ql; |
|||
|
N2 P 2 qz2 3 ql 2 qz2 |
z2 0 |
3 ql; |
|
|
z2 2l |
3 ql 2 q 2l 1 ql; |
N3 P 2 q 2l 0,2 P 3 ql 4 ql 0,2 3 ql 0,4 ql .
По этим значениям построим эпюру N (рис. 1.6, д).
а
б
в
г
д
е
ж
Рис. 1.6
26

2. Выражения для нормальных напряжений
Составим выражения для нормальных напряжений σ по всем участкам бруса, используя указанные на схеме бруса значения площадей сечения через неизвестную величину F .
Нормальное напряжение σ вычисляем для каждого участка бруса по формуле (1.3) как
σi Ni .
Fi
3 ql 1,5 ql ; 2F F
|
N2 |
3 ql |
2 qz2 |
z2 |
0 |
3 ql |
; |
|||||||
|
σ2 |
F |
||||||||||||
|
F2 |
F |
z2 |
2l |
3 ql 2 q 2l |
ql |
; |
|||||||
|
F |
F |
||||||||||||
|
σ3 |
N3 |
0,4 ql |
0,133 ql . |
||||||||||
|
F3 |
3F |
F |
3. Нахождение σmax и условие прочности
Условие прочности ступенчатого бруса при растяжении-сжатии по допускаемым нормальным напряжениям имеет вид (1.5), согласно которому
|
Ni |
σ . |
||||
|
σmax |
(1.15) |
||||
|
Fi max |
Значит, нужно выбрать из полученных значений нормальных напряжений σ наибольшее по модулю значение, здесь имеем
σmax 3Fql .
Согласно (1.15) получаем
3Fql .
Из этого условия вычислим требуемое значение F и назначим площади всех участков бруса, соблюдая указанное соотношение между ними:
|
F |
3 ql |
3 20 103 1,2 |
3,6 |
10 |
4 |
м |
2 |
3,6 см |
2 |
. |
|
|
σ |
200 106 |
||||||||||
27

Принимаем F 3,6 см2 . Назначим площади всех участков бруса, соблюдая указанные на схеме бруса соотношения между ними:
F1 2F 2 3,6 7,2 см2 ; F2 F 3,6 см2 ; F3 3F 3 3,6 10,8 см2 .
4. Эпюры нормальных напряжений и продольных перемещений
Вычислим значения нормальных напряжений по участкам бруса, используя полученные выше выражения.
|
σ |
1,5 ql |
1,5 20 103 1,2 |
100 10 |
6 |
Па 100 МПа; |
||||||||
|
1 |
F |
3,6 10 4 |
|||||||||||
|
z |
2 |
0 |
3 ql 3 20 103 1,2 200 106 Па 200 МПа; |
||||||||||
|
σ2 |
F |
3,6 10 4 |
|||||||||||
|
ql |
20 103 1,2 |
||||||||||||
|
z |
2 |
2l |
66,67 106 |
Па 66,67 МПа; |
|||||||||
|
F |
3,6 10 4 |
||||||||||||
|
σ3 |
0,133 ql |
0,133 20 103 |
1,2 |
88,89 |
10 |
6 |
Па 88,89 МПа. |
||||||
|
F |
3,6 10 4 |
||||||||||||
Откладывая полученные значения от базисной линии, построим эпюру распределения нормальных напряжений по длине балки (эпюру σ) (рис. 1.6, е).
Построим эпюры продольных перемещений δ. Перемещения δ поперечных сечений бруса вычисляют по (1.7) через продольные деформации участков бруса li . Сначаланайдёмдеформации li участковбруса.
Согласно формуле (1.6)
li li Ni d z , 0 EFi
где E – модуль упругости первого рода или модуль Юнга; Fi – площадь
поперечного сечения; li – длина участка бруса.
Заметим, что в случае постоянной по участку продольной силы
li NiFli .
E i
|
l1 |
N |
l |
3 ql |
3 ql |
l |
1,5 ql 2 |
1,5 20 103 1,2 |
2 |
||||||
|
l 1 |
1 |
d z1 |
d z1 |
2EF |
0 |
EF |
2 1011 3,6 10 4 |
|||||||
|
E F |
E 2F |
|||||||||||||
|
0 |
1 |
1 |
0 |
0,6 10 3 м 0,6 мм.
28
|
l2 |
N2 |
2l 3 ql |
2qz2 |
3 ql z2 2qz22 / 2 |
2l |
||||||||
|
l 2 |
d z2 |
EF |
d z2 |
EF |
0 |
||||||||
|
E |
F |
||||||||||||
|
0 |
2 |
2 |
0 |
|
3 ql 2l q(2l)2 |
2 ql2 |
2 20 103 |
1,22 |
3 |
м |
0,8 мм. |
|||||||||||||||||||
|
EF |
EF |
2 |
11 |
3,6 |
10 |
4 0,8 10 |
|||||||||||||||||||
|
10 |
|||||||||||||||||||||||||
|
l3 |
N |
l |
0,4 ql |
0,4 ql |
l |
0,133 ql 2 |
0,133 20 103 1,2 |
2 |
|||||||||||||||||
|
l 3 |
3 |
d z3 |
d z3 |
3EF |
0 |
EF |
2 1011 |
3,6 10 4 |
|||||||||||||||||
|
E |
F |
E 3F |
|||||||||||||||||||||||
|
0 |
3 |
3 |
0 |
0,53 10 4 м 0,053 мм.
Теперь определим продольные перемещения δi характерных сечений, обозначив сечения буквами A, B , C , D . Так как точка A находится в заделке, то перемещение A 0 . Перемещения сечений B , C , D определяем
с помощью (1.7):
B l 3 0,053 мм;
C l 3 l 2 0,053 0,8 0,747 мм;
D l 3 l 2 l1 0,053 0,8 0,6 1,347 мм.
На участке 2 эпюра продольных сил пересекает нулевую линию в точке K (рис. 1.6, д), в этом сечении будет перегиб на эпюре перемеще-
ний, поэтому определим координату z2K . Из условия N2K 0 получаем
|
Отсюда |
N2K 3 ql 2 qz2K 0 . |
|||||||||||||||
|
3 ql |
||||||||||||||||
|
z2K |
1,5l . |
|||||||||||||||
|
2 q |
||||||||||||||||
|
Вычислим продольную деформацию участка CK: |
||||||||||||||||
|
z2K |
N2 |
3 ql z2 |
qz22 |
1,5l |
2,25 ql 2 |
2,25 20 103 1,2 |
2 |
|||||||||
|
l CK |
d z2 |
EF |
0 |
EF |
2 1011 3,6 10 4 |
|||||||||||
|
E |
2 |
F |
||||||||||||||
|
0 |
2 |
|||||||||||||||
|
0,9 10 3 м 0,9 мм. |
||||||||||||||||
|
Тогда продольное перемещение сечения K согласно (1.7) |
||||||||||||||||
|
K B l BK C l CK 0,747 0,9 0,153 мм. |
||||||||||||||||
|
По полученным значениям построим эпюру продольных перемеще- |
||||||||||||||||
|
ний (рис. 1.6, ж). |
||||||||||||||||
|
Укажем max |
и проверим жёсткость при допускаемом продольном |
|||||||||||||||
|
перемещении. |
||||||||||||||||
|
29 |
Используем условие жёсткости (1.9), для которого выбираем из полученных значений наибольшее по модулю: max 1,347 мм. Тогда условие жёсткости принимает вид
δmax 1,347 мм δ 0,5 мм.
Как видим, условие жёсткости не выполняется. Необходимо назначить новые площади сечений, чтобы соблюдалось условие жёсткости, которое в нашем примере должно иметь вид
|
δmax δ 0,5 мм. |
||||||||||
|
Запишем δmax |
через нагрузку и жёсткость сечения EF : |
|||||||||
|
max D l 3 |
l 2 |
l1 |
0,133 ql2 |
2 ql |
2 |
1,5 ql2 |
3,367 ql2 |
. |
||
|
EF |
EF |
EF |
EF |
|||||||
Тогда условие жёсткости примет вид
|
3,367 ql2 |
. |
||||||||||||
|
EF |
|||||||||||||
|
Отсюда |
|||||||||||||
|
F |
3,367 ql2 |
3,367 20 103 1,22 |
9,697 10 |
4 |
м |
2 |
9,697 мм |
2 |
. |
||||
|
E |
2 1011 0,5 10 3 |
||||||||||||
|
Принимаем F 9,7 см2 и окончательно назначаем площади участков |
|||||||||||||
|
бруса: |
|||||||||||||
|
F 2F 2 9,7 19,4 см2 ; F F 9,7 |
см2 ; |
F 3F 3 9,7 29,1см2 . |
|||||||||||
|
1 |
2 |
3 |
5. Касательные и нормальные напряжения в наклонной площадке
Для опасного сечения бруса вычислим касательные и нормаль-
|
ные напряжения |
в наклонной площадке, |
проведённой под углом |
|
|
45 к оси бруса. |
|||
|
Напряжения подсчитаем по формулам (1.10), подставляя значения |
|||
|
нормальных напряжений в опасном сечении C: |
|||
|
cos2 cos2 45 |
88,89 |
44,45 МПа; |
|
|
2 |
2 |
||
|
sin 2 sin 2 45 |
44,45 МПа. |
||
|
2 |
2 |
2 |
|
|
30 |
6. Определение силы P0
Определим, какую силу P0 нужно приложить к свободному торцу бруса, чтобы вернуть его в первоначальное положение. Сечение D получило отрицательное перемещение δ D 1,347 мм. Чтобы вернуть сечение в
первоначальное положение, нужно приложить растягивающую силу Р0, которая растянет брус на 1,347 мм, т. е. деформация всего бруса от силы Р0
составляет l(P0 ) 1,347 мм. Записывая эту деформацию как сумму деформаций участков, получим уравнение
|
P |
l |
2 l |
l |
1,347 мм; |
||||||
|
0 |
E 2F |
EF E |
||||||||
|
3F |
||||||||||
|
P0 |
l |
17 |
1,347 мм. |
|||||||
|
EF |
||||||||||
|
6 |
Отсюда
P0 1,35 10 3 6 2 1011 3,6 10 4 47,6кН. 17 1,2
Задача4 Проектныйрасчёт ступенчатого статическинеопределимогобруса
Стальной ступенчатый брус (рис. 1.7, а) жёстко закреплён с торцов. Задана конфигурация бруса и известна внешняя нагрузка: l 0,6 м; P ql ;
q 80 кН/м.
Требуется
1.Используя условие равновесия и уравнение перемещений, найти величины реактивных сил, возникающих в жёстких заделках.
2.Построить эпюру продольных сил N.
3.Составить выражения для нормальных напряжений по всем участкам бруса, используя указанные на чертеже бруса значения площадей сечения через неизвестную величину F.
4.Установить max, составить условие прочности бруса по допускаемым напряжениям. Найти из этого условия требуемое значение F при
31
= 200 МПа и назначить площади всех участков бруса, соблюдая указанное соотношение между ними.
5.Построить эпюры нормальных напряжений и продольных пере-
мещений δ, считая модуль упругости E = 2· 5 МПа. Указать δmax и проверить жёсткость при допускаемом продольном перемещении [δ] = 0,5 мм. Если условие жёсткости не удовлетворяется, назначить новые площади сечений.
6.Для опасного сечения бруса вычислить касательные τα и нормаль-
ные α напряжения в наклонной площадке, проведённой под углом α = 45°
коси бруса.
7.Вычислить температурные напряжения, возникающие при повышении температуры среды на 40°. Принять коэффициент линейного удли-
нения = 1,25·10–5 1/град.
8. Найти величины реактивных сил, если между правой заделкой и торцом бруса будет зазор величиной 0,0001·L.
Решение
1. Вычисление реактивных сил
Обозначим реактивные силы, возникающие в жёстких заделках под нагрузкой как RA и RD (рис. 1.7, а). Их величины должны удовлетворять
|
уравнению равновесия всего бруса при растяжении-сжатии |
(1.1), т. е. |
|
пр z 0, которое принимает вид |
|
|
–RA ql ql RD 0. |
(1.16) |
Как видно, это уравнение содержит два неизвестных RA и RD , поэтому брус является статически неопределимым. Для нахождения RA и RD
необходимо составить еще одно уравнение – уравнение перемещений. При растяжении-сжатии ступенчатого бруса уравнение перемещений
записывают через продольные деформации участков li . Данный брус состоит из трёх участков, поэтому
|
l 1 |
l 2 |
l 3 0, |
(1.17) |
||||
|
где выражения деформаций участков бруса l 1 , |
l 2 |
и l 3 |
составляем по |
||||
|
(1.6) как |
l |
||||||
|
Ni |
|||||||
|
li |
i |
d z , |
|||||
|
EF |
|||||||
|
0 |
i |
где Ni – продольное усилие на рассматриваемом участке; E – модуль упругости первого рода или модуль Юнга; Fi – площадь поперечного сечения; li – длина участка бруса.
32
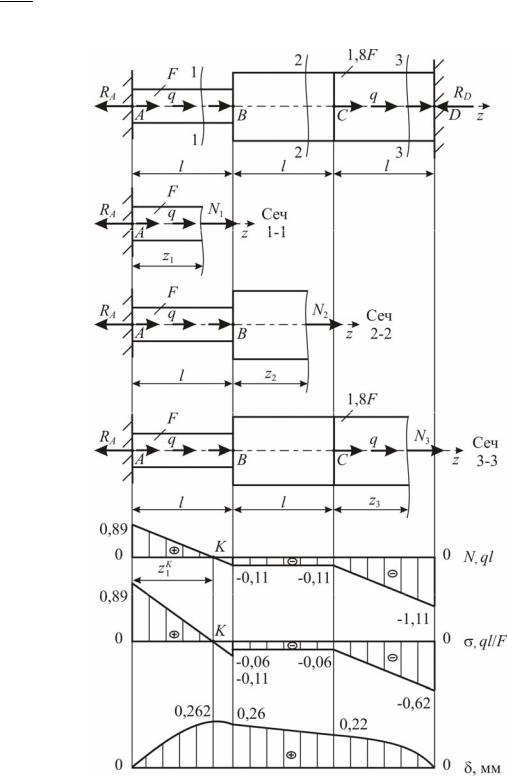
Заметим, что в случае постоянной по участку продольной силы
li NiFli .
E i
а
б
в
г
д
е
ж
Рис. 1.7
33
Сначала запишем для каждого участка бруса продольные усилия и абсолютные деформации. Продольные силы определяем методом сечений, рассматривая отсечённые части каждого участка (рис. 1.7, б, в, г), начиная со свободного конца. При этом продольную силу изображаем положительной, т. е. растягивающей рассматриваемый участок.
Испльзуя уравнение равновесия отсечённой части пр z 0, записываем последовательно продольные силы для каждого участка:
N1 RA qz1 ;
N2 RA ql ;
N3 RA ql qz3 ;
Составим выражения деформаций участков бруса l 1, l 2 и l 3 ,
причём площади сечения возьмём по конфигурации бруса через неизвестное значение F:
|
N |
1 |
l |
R |
A |
qz |
R |
z |
qz2 |
/ 2 |
l |
RA l 0,5ql2 |
||||||||
|
l |
dz |
1 |
dz |
A 1 |
1 |
; |
|||||||||||||
|
1 |
1 |
EF |
1 |
EF |
0 |
EF |
|||||||||||||
|
l1 |
EF1 |
0 |
|
N2 |
l |
RA ql |
RA z2 qlz2 |
l |
RA l ql 2 |
||||||||||||||||||
|
l2 |
dz2 |
dz2 |
1,8EF |
0 |
; |
||||||||||||||||||
|
EF |
E |
1,8F |
1,8EF |
||||||||||||||||||||
|
l2 |
2 |
0 |
l |
RA l 1,5ql 2 |
|||||||||||||||||||
|
RA z3 qlz3 qz32 / 2 |
|||||||||||||||||||||||
|
N3 |
l |
RA ql qz3 |
|||||||||||||||||||||
|
l3 |
dz3 |
dz1 |
1,8EF |
0 |
. |
||||||||||||||||||
|
EF |
E 1,8F |
1,8EF |
|||||||||||||||||||||
|
l |
3 |
0 |
|||||||||||||||||||||
|
3 |
Подставляя в (1.17) эти величины, получим уравнение перемещений, записанное через RA :
|
RA l 0,5ql 2 |
RA l ql 2 |
RA l 1,5ql 2 |
0. |
(1.18) |
|||
|
EF |
1,8EF |
1,8EF |
|||||
Уравнение равновесия (1.16) и уравнение перемещений (1.18) составляют систему 2 уравнений с двумя неизвестными – RA и RD ; решая
эту систему, найдём величины реактивных сил. Уравнение (1.18) есть уравнение с одним неизвестным RA . Тогда, умножая его на EF, получим
1,8 RA l 0,5ql 2 RA l ql 2 RA l 1,5ql 2 0 ;
34

3,8RA l 3,4ql 2 0 ;
RA 3,34,8ql 0,89ql .
Из уравнения (1.16) получим
RD –RA 2ql 0,89ql 2ql 1,11ql .
2. Построение эпюры продольных сил N
Подставив найденную реакцию RA в выражения продольных усилий по участкам, получим их значения:
|
N |
R |
A |
qz |
0,89ql qz |
z1 |
0 0,89ql; |
|||||
|
1 |
1 |
1 |
z |
l |
0,89ql ql 0,11ql; |
||||||
|
1 |
|||||||||||
|
N2 RA ql 0,89ql ql 0,11ql; |
|||||||||||
|
N3 RA ql qz3 0,11ql qz3 |
z3 |
0 |
0,11ql; |
||||||||
|
z3 |
l |
0,11ql ql 1,11ql. |
|||||||||
Откладывая от базисной линии эти значения, построим эпюру N
(рис. 1.7, в).
3. Выражения нормальных напряжений
Составим выражения нормальных напряжений для каждого участ-
|
ка вала по формуле (1.3) как σi |
Ni |
: |
|||||||||||||||||||
|
F |
|||||||||||||||||||||
|
i |
|||||||||||||||||||||
|
N1 |
z1 |
0 |
0,89 ql ; |
||||||||||||||||||
|
1 |
0,89 ql qz1 |
F |
|||||||||||||||||||
|
F1 |
z1 |
l |
0,89 ql ql |
0,11ql |
; |
||||||||||||||||
|
F |
F |
||||||||||||||||||||
|
2 |
N2 |
0,11ql |
0,06 ql |
; |
|||||||||||||||||
|
1,8F |
|||||||||||||||||||||
|
F2 |
F |
||||||||||||||||||||
|
N3 |
0,11ql qz3 |
z3 0 |
0,11ql |
0,06ql |
; |
||||||||||||||||
|
3 |
1,8F |
1,8F |
|||||||||||||||||||
|
F3 |
1,8F |
z3 l |
0,11ql ql |
0,62ql |
. |
||||||||||||||||
|
1,8F |
F |
||||||||||||||||||||
35

4. Условие прочности бруса
Условие прочности ступенчатого бруса при растяжении-сжатии по допускаемым нормальным напряжениям запишем по (1.5):
|
Ni |
σ . |
|||
|
σmax |
||||
|
Fi max |
Выбираем max из полученных выше значений нормальных напряжений σi как наибольшее по модулю:
max 0,89F ql .
Теперь условие прочности получаем в виде
0,89F ql .
Найдём из этого условия требуемое значение F и назначим площади всех участков бруса, соблюдая указанное соотношение между ними:
|
F |
0,89 ql |
0,89 80 103 0,6 |
2,136 10 |
4 |
м |
2 |
= 2,136 см |
2 |
. |
|
|
σ |
200 106 |
Принимаем F 2,2 см2 и назначаем площади всех участков бруса:
F1 F 2,2 см2 ; F2 F3 1,8F 1,8 2,2 3,96 см2 .
5. Эпюры нормальных напряжений и продольных перемещений
Вычислим значения нормальных напряжений по участкам бруса, используя полученные выше выражения:
|
z |
0 |
0,89ql 0,89 80 103 |
0,6 194 106 Па = 194 МПа; |
||||||||||||||||||||
|
1 |
F |
2,2 10 4 |
|||||||||||||||||||||
|
σ1 |
|||||||||||||||||||||||
|
0,11ql |
0,11 80 103 0,6 |
||||||||||||||||||||||
|
z |
l |
24 106 Па = –24 МПа; |
|||||||||||||||||||||
|
1 |
F |
2,2 10 4 |
|||||||||||||||||||||
|
σ |
2 |
0,06 ql |
0,06 80 103 0,6 |
13 10 |
6 |
Па = –13 МПа; |
|||||||||||||||||
|
F |
2,2 10 4 |
||||||||||||||||||||||
|
z |
0 |
0,06ql |
0,06 80 103 |
0,6 |
–13 10 |
6 |
Па = –13 МПа; |
||||||||||||||||
|
1,8F |
2,2 10 4 |
||||||||||||||||||||||
|
σ3 |
3 |
||||||||||||||||||||||
|
0,62ql |
0,62 80 103 |
0,6 |
|||||||||||||||||||||
|
z |
l |
–135 10 |
6 |
Па = –135 МПа. |
|||||||||||||||||||
|
F |
2,2 |
10 4 |
|||||||||||||||||||||
|
3 |
36
Откладывая полученные значения от базисной линии, построим эпюру распределения нормальных напряжений по длине балки (эпюру ) (рис. 1.7, е).
Построим эпюры продольных перемещений . Сначала подставим в полученные ранее выражения деформаций участков бруса найденные величины площадей и получаем значения деформаций:
|
l |
RA l 0,5ql 2 |
0,89ql2 0,5ql |
2 |
0,39ql 2 |
0,39 80 103 0,62 |
||||||||||||||||
|
1 |
EF |
EF |
EF |
2 1011 2,2 10 4 |
|||||||||||||||||
|
0,26 10 3 м = 0,26 мм; |
|||||||||||||||||||||
|
l2 |
RA l |
ql 2 |
0,89ql2 1ql2 |
0,11ql 2 |
0,11 80 103 |
0,62 |
|||||||||||||||
|
1,8EF |
1,8EF |
1,8EF |
1,8 2 1011 2,2 10 4 |
||||||||||||||||||
|
0,04 10 3 м = –0,04 мм; |
|||||||||||||||||||||
|
l3 |
RA l 1,5ql 2 |
0,89ql 2 1,5ql |
2 |
0,61ql 2 |
0,61 |
80 103 0,6 |
2 |
||||||||||||||
|
1,8EF |
1,8EF |
1,8EF |
1,8 2 |
1011 |
2,2 10 4 |
||||||||||||||||
0,22 10 3 м = –0,22 мм.
Определим продольные перемещения характерных сечений, обозначив сечения буквами A, B , C , D.
A 0, т. к. точкаA находится в заделке; перемещения сечений B , C , D определим с помощью (1.7):
δB l1 0,26 мм;
δC l1 l 2 0,26 0,04=0,22 мм;
D l 1 l 2 l 3 0,26 0,04 0,22 0.
Продольное перемещение в сечении D оказался равным нулю, т. к. это сечение находится в заделке.
По полученным значениям построим эпюры продольных перемещений (рис. 1.7, ж). Уточним линию на первом участке, где имеем линейный характер силы N1 и пересечение её эпюры с базисной линией в сече-
нии K при z 1 z K1 :
N K1 0,89ql qz K1 0 .
37

Вычислим координату z K1 0,89ql / q 0,89l . Перемещение этого сечения равно деформации участка AK, поэтому
|
δK lДК |
0,8l qz |
3 |
0,8ql |
dz3 |
q(0,8l)2 |
0,8ql 0,8l |
0,32ql2 |
0,64ql2 |
|||
|
EF3 |
2EF3 |
EF3 |
|||||||||
|
0 |
EF3 |
EF3 |
|
0,32ql2 |
0,32 105 103 0,42 |
4 |
||||||||||||||||||||
|
1,07 10 |
м 0,107 мм; |
|||||||||||||||||||||
|
EF |
11 |
1,5 1,68 10 |
4 |
|||||||||||||||||||
|
2 10 |
||||||||||||||||||||||
|
3 |
||||||||||||||||||||||
|
R |
z |
qz2 |
/ 2 |
0,89l |
0,89ql 0,89l 0,5q |
0,89l 2 |
0,40ql2 |
|||||||||||||||
|
K lAK |
A |
1 |
EF |
1 |
||||||||||||||||||
|
0 |
EF |
EF |
||||||||||||||||||||
|
0,40 80 103 0,62 |
0,262 10 |
–3 |
м = 0,262 мм. |
|||||||||||||||||||
|
2 |
11 |
2,2 10 |
4 |
|||||||||||||||||||
|
10 |
Отложив это значение, проводим кривую с перегибом в точке K. Проверим условие жёсткости, для этого из эпюры перемещений
возьмём δmax δK 0,262 мм и запишем δmax δK 0,262 < δ = 0,5 мм, значит, условие жёсткости выполняется.
6. Касательные и нормальные напряжения в наклонной площадке
Для опасного сечения бруса вычислим касательные τα и нормальныеα напряжения в наклонной площадке, проведённой под углом α = 45° к оси бруса. Напряжения на наклонных площадках вычисляют по известным формулам (1.10):
τα σ2 sin 2α 1942 sin 2 45 = 97 МПа ;
σα σ cos2 α 194 cos2 45 194 0,5 = 97 МПа .
7. Температурные напряжения
Вычислим температурные напряжения, возникающие при повышении температуры среды на 40°. Для этого составим уравнение перемещений (1.17), учитывая удлинение от температуры и сжатие от реакций, возникающих в заделках. При этом удлинение определяем по формуле
l t l NEtFl .
38
|
t |
l |
l |
l |
||||||||||||
|
RA |
1 |
2 |
3 |
α t (l1 l2 l3 ) |
|||||||||||
|
EF2 |
|||||||||||||||
|
EF1 |
EF3 |
||||||||||||||
|
или |
|||||||||||||||
|
t |
l |
l |
l |
||||||||||||
|
RA |
α t(l l l) |
||||||||||||||
|
1,8EF |
|||||||||||||||
|
EF |
1,8EF |
Отсюда
|
t |
3α t EF |
3 1,25 10 5 40 2 1011 2,2 10 4 |
3 |
||
|
R |
31,28 10 = 31,28 кН. |
||||
|
A |
2,11 |
2,11 |
|||
Вычислим наибольшие температурные напряжения σt , которые будут возникать в более тонком месте − на участке 1:
|
σ |
RAt |
31,28 103 |
142 106 Па= 142 МПа. |
||
|
F |
2,2 10 4 |
||||
|
t |
|||||
|
1 |
8. Влияние зазора на величину реакций
В случае зазора при действии температуры торец бруса переместиться за счёт деформации на величину зазора. Поэтому величины реактивных сил должны удовлетворять уравнению перемещений, в котором правая часть равна 0,0001·L1:
|
t |
l |
l |
l |
α t(l l l) 0,0001 l. |
|||
|
RA |
|||||||
|
1,8EF |
|||||||
|
EF |
1,8EF |
|
t |
(3α t 0,0001l) EF |
(3 1,25 10 5 40 0,0001 0,6) 2 1011 2,2 10 4 |
|||
|
R |
|||||
|
A |
2,11 |
2,11 |
|||
28 103 Н= 28 кН.
Как видим, значение температурных реакций при наличии зазора уменьшается.
39

Задача 5
Проектный расчёт стержневой статически неопределимой системы при растяжении и сжатии
В статически неопределимой стержневой системе абсолютно жёсткий брус AB опирается на шарнирно-неподвижную опору и прикреплен двумя упругими стержнями к неподвижной опорной поверхности (рис. 1.8, а). Брус несёт нагрузку известной величины: l 1,6 м, q = 20 кН/м; P 2 ql .
Требуется
1.Найти усилия в упругих стержнях, используя уравнения равновесия и уравнение перемещений.
2.Подобрать площади поперечных сечений стержней, используя условия прочности по допускаемым напряжениям и по методу предельного
состояния, если допускаемое напряжение = 200 МПа, предел текучести
т = 320 МПа, запас прочности n = 1,6.
3. Вычислить температурные напряжения, возникающие в стержнях при повышении температуры среды на 15 С. Принять коэффициент линейного удлинения = 1,25·10–5 1/град.
Решение
1. Нахождение усилий в стержнях
Статически неопределимые стержневые системы – это системы, в которых количество стержней превышает количество уравнений равновесия.
Брус АВ имеет шарнирно-подвижные опоры в точках А и В и шар- нирно-неподвижную в точке K. В опорах возникают реакции RAC, RBD, RK и HK (рис. 1.8, б). Для плоской системы можно составить три уравнения равновесия, а неизвестных четыре, значит, заданная система имеет одну «лишнюю» связь, и степень ее статической неопределимости 1.
При расчётах необходимо знать продольные силы, возникающие во всех стержнях. Для нахождения этих усилий дополнительно к уравнениям равновесия составляют уравнения, учитывающие характер деформации системы. Их называют уравнениями совместности деформаций (или уравнениями перемещений). Число их равно количеству «лишних» (с точки зрения статики) связей системы и характеризует степень её статической неопределимости. Использование уравнений перемещений основано на том, что деформации стержней можно выразить через неизвестные про-
дольные силы по формуле l EFNl и сравнить между собой.
40

Под действием внешней нагрузки брус АВ займет положение А1В1 (рис. 1.7, г). Горизонтальными перемещениями концов А и В пренебрегаем
|
в силу малости деформаций в таких несущих конструкциях. Отрезок АА1 |
||||||||||||||||||||||||||||||||||
|
есть деформация стержня АС, назовем ее l1 . |
На первоначальной длине |
|||||||||||||||||||||||||||||||||
|
стержня DВ отложим его новую длину DВ1 (считаем, что В1 |
В2 |
DВ). От- |
||||||||||||||||||||||||||||||||
|
резок ВВ2 – укорочение стержня |
DВ, |
обозначим |
его |
l2 . |
Из |
BB1B2 |
||||||||||||||||||||||||||||
|
h |
l2 |
|||||||||||||||||||||||||||||||||
|
. |
||||||||||||||||||||||||||||||||||
|
cos45 |
||||||||||||||||||||||||||||||||||
|
Запишем связь между деформациями l1 |
и l2 |
из подобия треуголь- |
||||||||||||||||||||||||||||||||
|
ников AA1K ~ BB1K : |
l1 |
h |
l1 |
lAK |
||||||||||||||||||||||||||||||
|
или |
lAK |
lBK |
h |
lBK |
||||||||||||||||||||||||||||||
|
l1 |
cos45 lAK |
l1 |
2 |
l |
l |
2 l |
2 |
. |
(1.19) |
|||||||||||||||||||||||||
|
l2 |
lBK |
l2 2 |
2l |
1 |
||||||||||||||||||||||||||||||
|
Выразим деформации l1 |
и |
l2 через продольные усилия, возни- |
||||||||||||||||||||||||||||||||
|
кающие в стержнях АС и DВ. Чтобы «увидеть» эти усилия, отсечём систе- |
||||||||||||||||||||||||||||||||||
|
му по шарнирам С и D, а для сохранения равновесия приложим в этих |
||||||||||||||||||||||||||||||||||
|
шарнирах реакции N1 и N2 (рис. 1.8, б), взяв направление в соответствии с |
||||||||||||||||||||||||||||||||||
|
деформацией удлинения l1 и укорочения l2 |
усилие N1 покажем растя- |
|||||||||||||||||||||||||||||||||
|
гивающим, а усилие N2 |
− сжимающим. Или выполнив разрез системы по |
|||||||||||||||||||||||||||||||||
|
шарнирам А и В (рис. 1.8, в), покажем усилиями N1 и N2 |
воздействие раз- |
|||||||||||||||||||||||||||||||||
|
резанных частей системы друг на друга. Здесь хорошо видно, |
что N1 и N2 |
|||||||||||||||||||||||||||||||||
|
вызывают соответственно растяжение и сжатие стержней. Как известно, |
||||||||||||||||||||||||||||||||||
|
деформации связаны с продольными усилиями как |
||||||||||||||||||||||||||||||||||
|
l |
N1l1 |
и l |
2 |
N2l2 |
. |
|||||||||||||||||||||||||||||
|
1 |
EF1 |
EF2 |
||||||||||||||||||||||||||||||||
|
Подставив эти выражения l1 |
и l2 |
в (1.19), получим уравнение сов- |
||||||||||||||||||||||||||||||||
|
местности деформаций: |
N1l1 |
2N2l2 |
||||||||||||||||||||||||||||||||
|
, |
||||||||||||||||||||||||||||||||||
|
EF |
EF |
|||||||||||||||||||||||||||||||||
|
где l1 l , l2 2l sin 45 ; |
1 |
2 |
||||||||||||||||||||||||||||||||
|
F1 2F ; |
F2 F . |
|||||||||||||||||||||||||||||||||
|
Тогда |
||||||||||||||||||||||||||||||||||
|
N1l |
2N2 2l 2 / 2 |
, |
||||||||||||||||||||||||||||||||
|
E2F |
EF |
|||||||||||||||||||||||||||||||||
|
и после сокращения это уравнение принимает вид |
||||||||||||||||||||||||||||||||||
|
N1 4N2 . |
(1.20) |
|||||||||||||||||||||||||||||||||
|
41 |
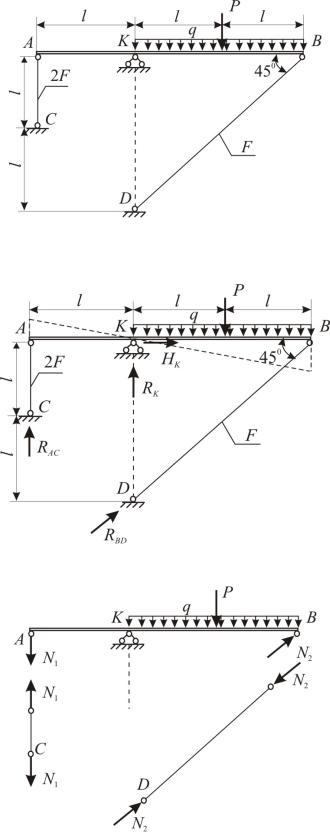
а
б
в
Рис. 1.8
42
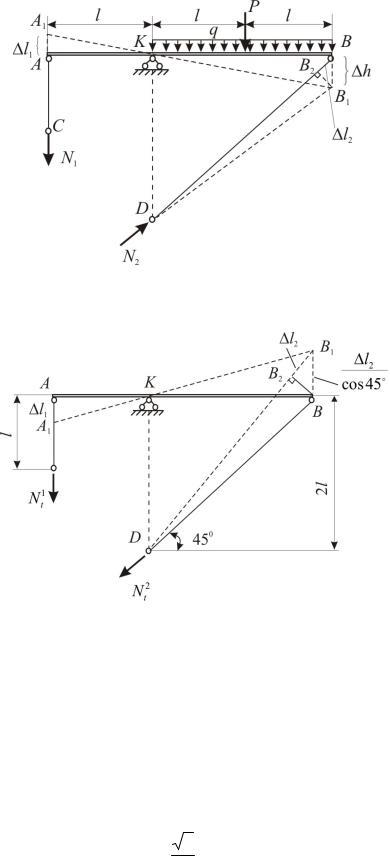
г
д
Рис. 1.8 (окончание)
Так как не требуется определить реакции в жёсткой опоре K, составим только одно уравнение равновесия ∑ мом К = 0:
N1l N2 2l cos45 Pl q2l 0,
или
N1 N2 2 22 2ql 2ql 0,
43
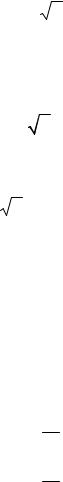
|
N1 |
2N2 |
4ql . |
(1.21) |
||||
|
Решаем систему уравнений |
(1.20) |
и (1.21). Подставим |
из (1.20) |
||||
|
N1 4N2 в (1.21), получим |
|||||||
|
4N2 2N2 4ql. |
|||||||
|
Отсюда найдём N2 |
4ql |
0,74ql , и по (1.20) N1 4N2 |
2,96ql . |
||||
|
(4 |
2) |
||||||
|
Положительные знаки N1 и N2 |
указывают на то, что выбранные на- |
||||||
|
правления их верны. |
2. Подбор размеров сечений стержней
Необходимые размеры поперечных сечений стержней определяют из условий прочности по допускаемым напряжениям или по предельному состоянию. В случае неодинакового сопротивления материала растяжению и сжатию условие прочности по допускаемым напряжениям имеет вид
σрmax NF σ р ,
N
σсmax F σ с .
Для нашего примера это условие прочности по допускаемым напряжениям запишем как
|
N1 |
[ ]; |
1 |
2,96ql |
200 |
10 |
6 |
; |
|||||
|
1 |
F1 |
2F |
||||||||||
|
или |
||||||||||||
|
N2 |
0,74ql |
6 |
||||||||||
|
2 |
[ ], |
2 |
200 |
10 . |
||||||||
|
F2 |
F |
|||||||||||
|
Отсюда получим два значения F: |
||||
|
F |
2,96 20 103 1,6 |
2,37 10 4 |
м2 2,37 см2 ; |
|
|
2 200 106 |
||||
и
F 0,74 20 103 1,6 1,18 10 4 м2 1,18см2. 200 106
44

Чтобы удовлетворить оба уравнения прочности, выбираем бóльшее
|
значение |
F 2,37 см2 и, округлив его, принимаем |
F 2,4 см2 |
, |
|
2 |
F1 4,8 см2 .
Найдём величины F1 и F2 по методу предельного состояния. При
расчёте по предельному состоянию учитываются пластические свойства металла. Считаем, что при действии внешних сил напряжения во всех стержнях равны пределу текучести т , а усилие в каждом стержне
Ni σт Fi . Такое стояние системы будет предельным, т. к. может вывести
её из строя.
Усилия в стержнях N1 т F1 и N2 т F2 . Выразим F1 и F2 через предельное (т. е. самое минимальное) значение площади сечения F пред , при котором и возникает предельное равновесие: F1 Fпред , F2 2Fпред. То-
гда N1 и N2 запишем как N1 σт F пред и N2 σт 2F пред .
Составим уравнение предельного равновесия, в которое войдут как внешняя нагрузка, так и усилия N1 и N2 . Воспользуемся уравнением
∑мом К = 0, оно принимает следующий вид:
σт 2F пред l σт F пред 2l cos 45 P l q2 l2 0.
|
σт 2Fпред σт Fпред |
2 2ql 2ql 0; |
||||||||||||||
|
σт 2Fпред σт Fпред |
2 4ql. |
||||||||||||||
|
Отсюда найдём предельное значение: |
|||||||||||||||
|
F |
пред |
3,2ql |
3,2 10 103 1,9 |
0,042 10 |
3 |
м |
2 |
0,42см |
2 |
; |
|||||
|
σт (2 |
2) |
3,41 420 106 |
|||||||||||||
|
F |
пред |
4ql |
4 20 103 |
1,6 |
1,17 10 |
4 |
м |
2 |
1,17см |
2 |
. |
||||
|
σт (4 |
2) |
320 106 (4 |
2) |
||||||||||||
Допускаемые значения площади сечения стержней F i , при которых система будет безопасной, можно найти, используя коэффициент запаса прочности n: увеличиваем полученное значение F пред в n раз, т. е.F i Fi n . В нашем случае F F пред n 1,17 1,6 1,87см2 . Тогда при-
нимаем площади сечений F1 2 F 3,74см2 и F2 F 1,87см2 . Как и сле-
довало ожидать, эти величины F получились меньше, чем по методу допускаемых напряжений.
45

3. Вычисление температурных напряжений
Найдём напряжения t , появляющиеся при повышении температуры
среды на 15 ºС. В статически неопределимых системах с повышением температуры окружающей среды и при отсутствии внешней нагрузки возникают напряжения, т. к. каждый стержень стремится удлиниться на величинуlt tº l , а этому препятствует другие стержни и опоры системы
(рис. 1.8, д). В результате в стержнях возникают продольные усилия Nt . Здесь деформация каждого стержня l слагается из температурной lt и деформации, полученной от возникающего продольного усилия Nt :
lNt NEFt l ,
т. е. деформация стержня
l t l NEtFl .
Методика определения усилий Nt и напряжений t остается прежней,
как и при нахождении усилий N и напряжений от внешней нагрузки. Пусть при повышении температуры брус АВ займет положение А1В1.
Тогда стержень АС получит сжатие на величину lt1 = АА1, стержень DВ – растяжение на lt2 = ВВ2 (рис. 1.8, д). Предположим направление усилий Nt1 и Nt2 растягивающими и запишем деформации стержней:
|
l |
1 |
t l |
N1 |
l |
; l |
2 |
t |
2l |
N 2 |
2l |
. |
|
|
t |
t |
|||||||||||
|
t |
E2F |
t |
cos45 |
EF cos45 |
||||||||
Уравнение равновесия ∑ мом К = 0 и уравнение перемещенийl1 
|
Nt1 |
l Nt2 |
2l cos45 ; |
|||||||||
|
1 |
2 |
||||||||||
|
Nt l |
2l |
Nt 2l |
|||||||||
|
α t l |
2 |
α t |
. |
||||||||
|
E2F |
cos45 |
||||||||||
|
EF cos45 |
Отсюда вычисляем температурные усилия:
Nt2 0,91 t EF 0,91 1,25 10 5 15 2 1011 2,4 10 4
8,19 103 Н 8,19кН;
Nt1 4Nt2 32,76 кН.
46
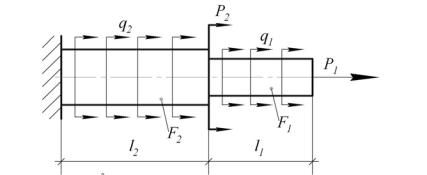
Как видно, стержни АС и DВ испытывают сжатие, при котором возникают температурные напряжения
|
1 |
N1 |
32,76 103 |
6 |
|||||||||||
|
t |
t |
4,8 10 4 |
68,25 10 |
Па 68,25 МПа; |
||||||||||
|
F |
||||||||||||||
|
1 |
||||||||||||||
|
2 |
N 2 |
8,19 103 |
34,13 10 |
6 |
Па 34,13 МПа. |
|||||||||
|
t |
t |
2,4 10 4 |
||||||||||||
|
F |
||||||||||||||
|
2 |
Задача 6 Проверочный расчёт ступенчатого бруса
Для ступенчатого бруса (рис. 1.9) известна внешняя нагрузка, заданы площади поперечного сечения и длины участков.
Рис. 1.9
Требуется
1.Построить эпюры продольных сил N, нормальных напряжений σ,
относительных деформаций и продольных перемещений δ. Принять модуль упругости E = 2· 5 МПа.
2.Указать опасное сечение и значение σmax, проверить прочность при допускаемом напряжении [σ] = 200 МПа. Если условие прочности не удовлетворяется, указать при каких размерах площади сечений оно выполнимо.
3.Указать значения max и δmax, проверить жёсткость при допускаемой относительной деформации = 0,005 и допускаемом продольном перемещении [δ] = 0,5 мм. Если условие жёсткости не удовлетворяется, указать, при каких размерах площади сечений оно выполнимо.
47

4. Для опасного сечения бруса вычислить касательные τα и нормальные α напряжения в наклонной площадке, проведённой под углом α = 45º к оси бруса.
Решение
1. Построение эпюр продольных сил, нормальных напряжений, относительных деформаций и продольных перемещений
В этой задаче использована унифицированная схема ступенчатого бруса при растяжении-сжатии, которая изображена на рис. 1.9. В ней в начале каждого участка приложены сосредоточенные силы Р, на каждом участке действует распределённая нагрузка интенсивности q.. Принимаем следующее правило знаков нагрузки: за положительное считаем растягивающее направление.
Выполним расчёт при следующих значениях. Сосредоточенные силы в начале участков Р1 = –60 кН и Р2 = 0; интенсивность распределённой нагрузки по участкам q1 = 0 и q2 = 150 кН/м; длины участков l1 = 0,5 м и l 2 = 0,6 м; площади сечений участков F1 = 6 см2 и F2 = 5 см2.
Сначала по исходным данным изобразим в масштабе заданный брус и действующую на него нагрузку (рис. 1.10, б). Брус разделим на два грузовых участка, здесь нумерацию участков удобно брать со свободного края, поэтому начало 1-го участка положим на торце бруса.
Для оценки прочности и жёсткости бруса, которые выполняются в 1, 2 и 3-м пунктах задачи, необходимо иметь значения продольных сил N, напряжений σ деформаций ε и перемещений δ на каждом участке. Запишем алгебраические выражения и подсчитаем значения этих величин, используя метод сечений и формулы напряжений и деформаций.
1-й участок 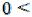
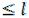
(рис. 1.10, а, б), удалённого от начала 1-го участка на расстоянии z1, продольную силу N1, напряжение σ1 и относительную деформацию ε1. Используя формулу продольной силы (1.2) для унифицированного нагружения, формулу напряжений (1.3) и закон Гука, по которому σ1 = ε1 E , получим
|
N P q z |
60кН; σ |
N1 |
60 103 |
100МПа; |
||||
|
F1 |
6 10 4 |
|||||||
|
1 1 |
1 1 |
1 |
||||||
|
ε1 |
σ |
100 106 |
50 10 5 0,5 10 3 . |
|||||
|
1 |
11 |
|||||||
|
E |
||||||||
|
2 10 |
2-й участок 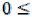
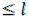
(рис. 1.10, а, б), удалённом от его начала на расстоянии z2, согласно (1.2), (1.4) и закону Гука имеем
48

|
N2 N1(l1) P2 |
q2 z2 |
60 150 z2 , |
|||||||||||||||||
|
при z2 0 |
N2 60кН, при z2 l2 |
N2 60 150 0,6 30 кН; |
|||||||||||||||||
|
σ |
N |
2 |
( 60 150 z |
2 |
) 103 |
( 120 300 z |
) 106 , |
||||||||||||
|
2 |
F |
5 10 4 |
2 |
||||||||||||||||
|
2 |
|||||||||||||||||||
|
при z2 0 σ2 |
120МПа, при z2 l2 σ2 |
60 МПа; |
|||||||||||||||||
|
σ |
( 120 300 z |
2 |
) 106 |
||||||||||||||||
|
ε2 |
2 |
( 60 150 z2 ) 10 5 |
( 0,6 1,5 z2 ) 10 3 , |
||||||||||||||||
|
2 1011 |
|||||||||||||||||||
|
E |
|||||||||||||||||||
|
при z2 0 |
ε2 |
0,6 10 3 , при z2 l2 ε2 |
0,3 10 3 . |
Используя полученные значения продольных сил, напряжений, относительных деформаций, построим эпюры этих величин непосредственно под брусом и подпишем их характерные значения (рис. 1.10, в, г, д).
Перейдём к перемещениям δ, необходимым для решения 3-го пункта задачи. Составим выражения продольных смещений δ характерных поперечных сечений А, В, С. Для этого необходимо знать абсолютные деформации участков li , которые вычисляются по формуле (1.6):
li li Ni d z . 0 EFi
Подставим полученные значения продольных сил N1 и N2, заданные площади сечения и длины участков, получим следующие абсолютные деформации участков:
|
l1 N1 |
N1 l1 |
σ1 l1 |
3 |
|||||||||
|
l1 0 |
dz2 |
E |
ε1 l1 0,5 10 |
0,5 |
||||||||
|
EF |
EF |
|||||||||||
|
1 |
1 |
1 |
||||||||||
|
= 0,25·10–3м = |
0,25 мм; |
|||||||||||
|
l2 0l2 |
N2 |
dz2 |
0l2 2 dz2 |
0l 2 |
( 60 150 z2 ) 10 5 dz2 |
|||||||
|
EF |
||||||||||||
|
2 |
||||||||||||
|
( 60 z |
150 z |
2 / 2) 10 5 ( 60 0,6 150 0,62 / 2) 10 5 9 10 5 м = –0,09 мм. |
||||||||||
|
2 |
2 |
Зная абсолютные деформации участков, подсчитаем продольные смещения указанных характерных сечений. Реальное перемещение сечения заделки отсутствует, поэтому запишем перемещение δА = 0.
49
а
б
в
г
д
е
Рис. 1.10
50
Первое сечение 2-го участка (сечение В) получило перемещение δВ, которое равно деформации этого участка: δВ = l2 0,09 мм. Первое сечение 1-го участка (это сечение С) получило перемещение
δС = δВ l1 0,09 ( 0,25) 0,34мм.
В нашем примере наклонная прямая на эпюре N (рис. 1.10, в) пересекает ось на расстоянии z0 от начала 2-го участка (обозначим это сечение К). Как известно, на эпюре перемещений в этом сечении ожидается экстремум − перегиб кривой перемещений. В сечении К сила N= 60 150z0 0 .
Отсюда абсцисса этого сечения
z0 Nq 15060 0,4м.
Необходимое значение экстремального перемещения δК (перемещения при z = z0) определяем на основании (1.7) как разницу между перемещением первого сечения и деформацией куска z0. При этом для деформации куска z0 используем полученное ранее выражение деформации 2-го участка, но только в нём укажем пределы интегрирования от 0 до z0 = 0,4 м. Вычисление в миллиметрах имеет следующий вид:
|
δК δВ 0z0 |
N2 |
dz2 0,11 ( 0,60 z2 1,50 z2 |
2 / 2) |
0z0 |
|||
|
EF |
|||||||
|
2 |
0,11 ( 0,60 0,4 1,50 0,42 / 2) 0,09 0,12 0,03 мм.
Отложив полученное значение от базисной линии на эпюре перемещений (рис. 1.10, е), проводим кривую с перегибом в сечении К.
2–3. Проверка условий прочности и жёсткости бруса
Теперь для ответа на пункты 2–3 назовём максимальные напряжения σmax, деформации εmax, перемещения δмах и сделаем выводы о прочности и жёсткости бруса при заданных величинах допускаемых напряжений [σ] = 200 МПa, деформаций [ε] = 0,005 и перемещений [δ] = 0,5 мм.
Условие прочности имеет вид
σmax = 100 МПа < [σ] = 200 MПa,
и, следовательно, прочность бруса обеспечена; запишем условие жёсткости:
εmax= < [0,0006]= 0,005; δmax= 0,34мм < [δ] = 0,5 мм,
значит, жёсткость бруса обеспечена.
51

4. Вычисление напряжений в наклонной площадке
Для опасного сечения бруса вычислим касательные τα и нормальные
α напряжения в наклонной площадке, проведённой под углом α = 45º к оси бруса. Опасным сечением является сечение, в котором нормальные напряжения максимальны по абсолютной величине: в нашем примере равноопасны все сечения 2-го участка и σmax = 100 МПа. Вычислим напряжения в наклонной площадке по (1.10):
σα σmax cos2 45 100( 22 )2 50 МПа;
τα σmax2 sin 90 σmax2 1002 50 МПа .
Как видно, эти напряжения не превышают допускаемых значений, и прочность в наклонной площадке под углом α = 45 к оси бруса обеспечена.
Задача 7 Проверочный расчёт ступенчатого статически неопределимого бруса
Стальной ступенчатый брус (рис. 1.11) жёстко защемлён с торцов и несёт нагрузку известной величины. Площади поперечного сечения и длины участков заданы.
Рис. 1.11
Требуется
1.Используя условие равновесия и уравнение перемещений, найти величины реактивных сил, возникающих в жёстких заделках.
2.Построить эпюры продольных сил N, нормальных напряжений σ,
относительных деформаций и продольных перемещений δ.
3. Указать опасное сечение и значение σmax, проверить прочность при допускаемом напряжении [σ] = 200 МПа. Если условие прочности не удовлетворяется, указать, при каких размерах площади сечений оно выполнимо.
52
4.Указать значения max и δmax, проверить жёсткость при допускаемой относительной деформации = 0,005 и допускаемом продольном перемещении [δ] = 0,5 мм. Если условие жёсткости не удовлетворяется, указать, при каких размерах площади сечений оно выполнимо.
5.Для опасного сечения бруса вычислить касательные τα и нормаль-
ные α напряжения в наклонной площадке, проведенной под углом α = 45 к осибруса.
6. Вычислить температурные напряжения, возникающие в брусе при повышении температуры среды на 50 С. Принять коэффициент линейного удлинения = 1,25·10–5 1/град.
7. Определить изменение величины реактивных сил, если между левой заделкой и торцом бруса будет зазор величиной 0,0001·L1.
Решение
1. Вычисление реактивной силы заделки
В этой задаче использована унифицированная схема ступенчатого бруса при растяжении-сжатии. Пусть в нашем примере заданы следующие величины: сосредоточенная сила Р = –30 кН; интенсивность распределённой нагрузки по участкам q1 = 60 кН/м, q2 = 0; длины участков l1 = 0,5 м, l 2 = 0,6 м; площади сечений участков F1 = 5 см2, F2 = 3 см2.
Сначала по исходным данным изобразим в масштабе заданный брус и действующую на него нагрузку (рис. 1.12, б). Брус имеет два грузовых участка (нумерацию участков начинаем справа) и две заделки, в которых возникают реактивные силы RA и RВ. Для решения задачи необходимо най-
ти величины этих сил. Составим уравнение равновесия бруса по (1.1)
пр z 0:
RA 30 60 0,5 RB 0.
Как видно, в уравнении имеем два неизвестных, и задача отыскания реакций является статически неопределимой. Составим дополнительное уравнение − уравнение перемещений, записав перемещение правой заделки и приравняв его нулю. Используем (1.6), запишем перемещение как сумму деформаций от каждого воздействия, начиная с левого торца бруса. Получим
|
R |
( |
0,5 |
0,6 |
) |
30 0,5 103 |
60 103 0,52 / 2 |
0. |
||||
|
A |
E 5 |
10 4 |
E 3 |
10 4 |
E 5 10 4 |
E |
5 10 4 |
||||
Отсюда RA = 5 кН, а из уравнения равновесия найдём вторую реак-
цию:
RВ = 5 кН.
53

2. Построение эпюр продольных сил, нормальных напряжений, относительных деформаций и продольных перемещений
Для оценки прочности и жёсткости бруса необходимо найти значения и построить эпюры продольных сил N, нормальных напряжений σ, от-
носительных деформаций и продольных перемещений δ. Запишем требуемые алгебраические выражения и вычислим значения, используя метод сечений и известные формулы.
1-й участок 
расстоянии z1 продольная сила N1, напряжение σ1 и относительная деформация ε1 согласно (1.2), (1.3) и закону Гука, по которому σ1 E ε1 , имеем
N1 RB 60z1 5 60z1,
|
N |
1 |
( 5 60z |
)103 |
6 |
|||||||||||
|
σ |
1 |
( 10 120z )10 |
, |
||||||||||||
|
1 |
|||||||||||||||
|
F1 |
5 10 4 |
1 |
|||||||||||||
|
при z1 0 |
σ1 10 МПа, при z1 |
l1 |
0,5м σ1 |
50МПа; |
|||||||||||
|
ε |
σ |
( 10 120z )106 |
( 5 60z )10 |
5 |
, |
||||||||||
|
1 |
1 |
||||||||||||||
|
1 |
E |
2 1011 |
1 |
||||||||||||
|
при z 0 ε |
0,5 10 4 , при z |
l |
0,5 м ε |
2,5 10 4. |
|||||||||||
|
1 |
1 |
1 |
1 |
1 |
2-й участок
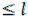
|
N N при z1 =l1 P 25 30 5кН, |
σ2 |
N |
2 |
5 103 |
16,7 МПа, |
|
|
F2 |
3 10 |
4 |
||||
|
2 |
1 |
|||||
|
ε2 = |
σ |
2 |
16,7 106 |
8,35 10 5 |
0,835 10 4 |
0,84 10 4 . |
|
|
11 |
|||||||
|
E |
|||||||
|
2 10 |
По полученным значениям продольных сил, напряжений, относительных деформаций непосредственно под брусом построим эпюры этих величин и подпишем их характерные значения (рис. 1.12, в, г, д).
Перейдём к перемещениям. Составим выражения продольных смещений δ характерных поперечных сечений А, В, С. Для этого вычислим абсолютные деформации участков по формуле
l 0l EFN dz 0l ε dz.
54
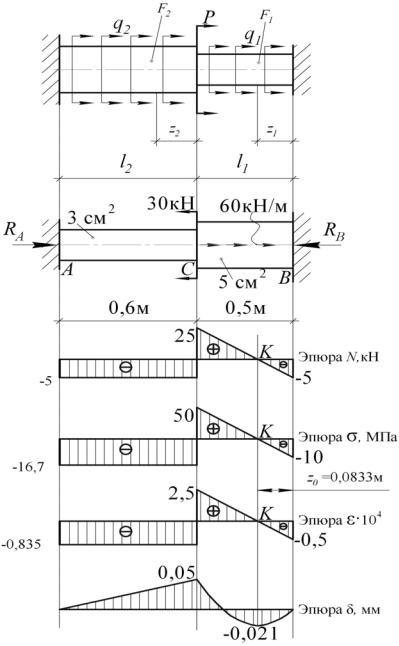
а
б
в
г
д
е
Рис. 1.12
Получаем следующие значения:
|
l1 0l1 |
N1 |
dz1 0l1 ε1 dz1 0l1 ( 5 60z1)10 5 |
dz1 |
||||||
|
EF |
|||||||||
|
1 |
|||||||||
|
( 5z |
60z 2 |
/ 2) 10 5 |
l1 0,5 |
5 10 5 м = 0,05мм; |
|||||
|
1 |
1 |
0 |
|||||||
55

|
l2 0l 2 |
N2 |
dz2 0l 2 ε2 dz2 0l 2 ( 0,835) 10 4 dz2 0,835 10 4 z2 |
l 2 0,6 |
||
|
EF |
|||||
|
2 |
|||||
|
0,5 10 4 м 0,05 мм. |
Реальное перемещение сечения заделки отсутствует, поэтому запишем перемещение δВ = 0. Последнее сечение 1-го участка (сечение С) получило перемещение δС, которое равно деформации этого участка δС = l1 0,05мм. Последнее сечение 2-го участка (сечение А) не имеет
смещения, т. к. в нём заделка. Действительно, получаем
δА = l1 l 2 0, 05 ( 0, 05) 0.
На эпюре сил N наклонная прямая пересекает ось (рис. 1.12, б) на расстоянии z0 от начала 1-го участка (это сечение К). В этом сечении на эпюре перемещений ожидается экстремум (перегиб кривой перемещений). Используя выражение продольной силы на 1-м участке, запишем уравнение NК = 0:
5 60z0 0.
Отсюда
z0 605 0,083 м.
Зная абсциссу z0 сечения К, найдём значение экстремального перемещения δК (перемещения при z = z0) на основании (1.7) как сумму перемещения δВ и деформации куска z0:
δК δВ 0z0 ε1 dz1 0 0z0 ( 5 60z1)10 5 dz1 ( 5z0 60z02 / 2)10 5
( 5 0,0833 60 0,08332 / 2)10 5 0,208 10 5 м 0,0021мм.
Отложив полученные значения перемещений, построим под брусом эпюру δ (рис. 1.12, е).
3–4. Проверка условий прочности и жёсткости бруса
Далее, для ответа на пункты 3–4, назовём максимальные напряжения σmax, деформации ε мах, перемещения δмах и сделаем выводы о прочности и жёсткости бруса при заданных величинах допускаемых напряжений [σ] = 200 МПa, деформаций [ε] = 0,005 и перемещений [δ] = 0,5 мм:
σmax = 50 МПа < [σ] = 200 MПa; εmax = 0,00025 < [ε] = 0,005; δmах = 0,05 мм < [δ] = 0,5 мм.
Следовательно, прочность жёсткость бруса обеспечена.
56

5. Вычисление напряжений в наклонной площадке
Для опасного сечения бруса вычислим касательные τα и нормальныеα напряжения в наклонной площадке, проведённой под углом α = 45 к оси бруса. Опасным сечением является сечение, в котором нормальные напряжения максимальны по абсолютной величине: в нашем примере это последнее сечение 1-го участка и σmax = 50 МПа. Вычислим напряжения в наклонной площадке:
σα= σmax cos2 45 50( 22 )2 25МПа; τα σmax2 sin90 σmax2 502 25МПа.
6. Вычисление температурных напряжений
Найдём температурные напряжения, возникающие в брусе при повышении температуры среды на 45 С. Для этого составим уравнение перемещений, учитывая удлинение от температуры и сжатие от реакций, возникающих в заделках:
Rt A( EFl1 1 EFl2 2 ) α t(l1 l2 ) 0.
Отсюда
Rt 1,25 10 5 50(0,5 0,6)2 1011 45,8 кН. A (0,5/5 0,6/3)104
Вычислим наибольшие температурные напряжения σt , которые будут возникать в более тонком месте − на 2-м участке:
|
Rt |
45,8 103 |
|||
|
σt |
A |
3 10 4 |
152,8МПа. |
|
|
F |
||||
|
2 |
7. Влияние зазора на величину реакций
Оценим влияние зазора на величину реакций от нагрузки. В случае зазора при действии нагрузки торец бруса переместиться за счёт деформации на величину зазора. Поэтому величины реактивных сил должны удовлетворять уравнению перемещений, в котором правая часть равна
0,0001·L1:
|
R |
A |
( |
0,5 |
0,6 |
) |
30 0,5 103 |
60 103 0,52 |
/ 2 |
0,0001 |
0,5. |
||
|
E 5 |
10 4 |
E 3 |
10 4 |
E 5 10 4 |
E 5 10 4 |
|||||||
Получаем RA = 1,7 кН, RВ = 1,7 кН. Как видим, значение реакций при наличии зазора уменьшается.
57
12-я лекция, 2010
8. ИСТЕЧЕНИЕ ЖИДКОСТИ
ЧЕРЕЗ ОТВЕРСТИЯ И НАСАДКИ
8.1 Истечение через отверстия в тонкой стенке и насадки (короткие трубки)
при постоянном напоре.
8.2. Истечение при совершенном сжатии.
8.3 Скорость истечения при совершенном сжатии. Коэффициенты:ε, ξ, φ, μ
8.4 Истечение при несовершенном сжатии
8.5. Истечение под уровень
8.6. Истечение через насадки при постоянном напоре.
8.7 Первый режим течения.
8.8 Второй режим истечения
8.1. Истечение через
отверстия и насадки (короткие трубки)
при постоянном напоре.
Рассматривается
процесс истечение жидкости из резервуаров через отверстия и насадки в атмосферу
и в пространство, заполненное жидкостью.
При истечении запас
потенциальной энергии жидкости в
резервуаре, переходит в кинетическую энергию свободной струи, при переходе есть
потери энергии на трение и завихрение
частиц жидкости.
Задачей изучения
процесса истечения является определение скорости истечения и расхода жидкости.
Истечение
производится из резервуара с жидкостью под давлением Р0 на
свободной поверхности через круглое отверстие в тонкой стенке на глубине (во
много раз большей диаметра отверстия) Н0 >> dот (рис. 12.1).
Через отверстие
жидкость вытекает в воздушное пространство с давлением Р1.
Отверстие в стенке
имеет острую кромку. Частицы жидкости приближаются к отверстию из всего
прилежащего объема, двигаясь ускоренно по различным плавным траекториям (см.
рис.12.1б). Струя отрывается от стенки у кромки отверстия и затем сжимается. Формирование
сжатого сечения струи происходит на расстоянии
примерно одного диаметра отверстия.
Сжатие струи происходит
при плавном переходе от различных направлений движения жидкости в резервуаре.
12.2. Истечение при
совершенном сжатии.
Совершенным сжатием называется наибольшее
сжатие струи, когда диаметр отверстия во
много раз меньше напора Н0.
Н0 >> dот
В этом случае боковые
стенки и свободная поверхность жидкости не влияют на поток жидкости к отверстию.
Сжатие струи оценивается
коэффициентом сжатия ε, равным отношению площади
поперечного сечения струи к площади отверстия
ε = Sc/S0 = (dc/d0)2. (12.1)
Для определения
скорости истечения и расхода из отверстия запишем уравнение Бернулли для движения
жидкости от свободной поверхности «0 – 0» в резервуаре и сечением
струи «1 – 1» (на рис.12.1а).
В рассматриваемом
случае уравнение Бернулли записывается для установившейся скорости, истечение происходит под постоянным напором,
над свободной поверхностью «0 – 0» давление
равно Р0, скорость
также равна нулю.
В сечении «1 – 1», струя примет цилиндрическую форму, давление Р1, скорость V1 предстоит определить из уравнения Бернулли для
потока реальной жидкости.
где ξ—
коэффициент, характеризующий сопротивление отверстия, 
для потока вязкой жидкости, характеризующий неравномерность распределения
скоростей в потоке.
Если умножить
числитель и знаменатель выражения для α на ρ/2, можно убедиться, что α
является отношением действительной кинетической энергии потока в данном сечении
к кинетической энергии этого потока в этом сечения при равномерном распределении скоростей.
Выделив сумму
геометрического и пьезометрического напора Н = Н0 + (Р0 – Р1)/(ρg), получаем выражение,
связывающее скорость истечения и скоростной напор.
12.3 Скорость истечения
реальной жидкости при совершенном сжатии.
Коэффициенты:ε, ξ, φ, μ
Из выражения для
гидростатического напора, получим формулу для определения скорости истечения из
отверстия с острой кромкой для реальной жидкости
, (12.2)
где φ —
коэффициент скорости
. (12.3)
Для идеальной
жидкости, так как у нее отсутствует вязкость, трения и потерь на трение
нет ξ = 0, α = 1, следовательно,
φ
= 1.
Скорость
истечения идеальной жидкости из отверстия с острой кромкой
(12.4)
Из формулы (12.2) можно заключить, что коэффициент
скорости φ есть отношение скорости истечения реальной жидкости к скорости истечения
идеальной жидкости.
, (12.5)
Скорость
истечения реальной жидкости меньше идеальной
из-за вязкости и трения, поэтому коэффициент скорости φ всегда меньше единицы.
Измерения
показывают, что в средней части сечения струи эпюра скоростей является
равномерной, поэтому скорость в средней части струи близка к идеальной , наружный слой жидкости притормаживается при трении о края
стенки отверстия. Коэффициент φ
рассматривается, как коэффициент по средней скорости.
Умножив скорость истечения на площадь сечения струи, получим
выражение для расхода жидкости через отверстие с острой кромкой при совершенном
сжатии
. (12.6)
Коэффициентом
расхода μ называют произведение
значений коэффициентов сжатия ε и скорости
φ
μ = ε * φ.
Формула для
расхода через отверстие с острой кромкой с учетом выражения для μ
(12.7) или
(12.8)
где ΔР
— расчетная разность давлений, под действием которой происходит истечение.
По этим формулам
определяется расход для всех случаев связанных с истечением из отверстия с острой кромкой и через насадки различных
форм.
Из уравнения (12.7)
следует, что
(12.9)
Коэффициент
расхода есть отношение действительного
расхода Q к расходу идеальной
жидкости Qи,
определенному по ее скорости . Действительный
расход всегда меньше расхода идеальной жидкости, следовательно, коэффициент
расхода всегда меньше единицы из-за сжатия струи и трения.
Коэффициенты
сжатия струи ε, сопротивления ξ, скорости φ, расхода μ = ε * φ зависят от
типа отверстия и насадка и от числа Рейнольдса.
На рис. 12.2
показаны составленные Альтшулем зависимости
для коэффициентов ε, φ и μ
для круглого отверстия в функции
числа Rеи, подсчитанного по
скорости истечения идеальной жидкости
Rеи=Vиd/ν = .
Увеличение числа Re означает
уменьшение сил вязкости, поэтому коэффициент φ возрастает в связи
с уменьшением коэффициента сопротивления ξ
(влияние трения становится меньше), коэффициент ε уменьшается из-за уменьшения торможения жидкости
у кромки отверстия и увеличения радиусов кривизны струи на входе в цилиндрическую
часть. При Rеи
→∞ значения коэффициентов приближаются к φ→1
и ε→0,6
и соответствуют истечению идеальной жидкости.
Коэффициент
расхода μ, определяемый
произведением ε на φ с увеличением Re сначала растет, что связано с сростом
φ,
а затем уменьшается в связи со
значительным падением ε
и при больших Rеи
равен μ = 0,60÷061.
В области малых Re (Rеи < 25) роль
вязкости велика, торможение жидкости у кромки значительно так, что сжатие струи отсутствует ε
= 1, φ = μ. В этом
случае можно пользоваться формулой:
(12.10)
12.3. Истечение при
несовершенном сжатии
Несовершенным
сжатием струи тогда, когда на формирование струи оказывает влияние близость боковых
стенок резервуара.
Боковые стенки успевают
направлять жидкость при подходе к отверстию, и струя сжимается в меньшей степени, чем при истечении
из резервуара неограниченных размеров при совершенном сжатии. Увеличивается коэффициент сжатия и коэффициент расхода.
При истечении из
цилиндрического резервуара через круглое отверстие, расположенное в центре торцевой
стенки при больших числах Re, коэффициент сжатия ε1 можно
находить по формуле Жуковского для идеальной жидкости
ε1 = 0,57 +0,043/(1,1 – n)
(12.11)
где n = S0/S1 отношение площади
отверстия S0 к
площади S1 поперечного
сечения резервуара.
Коэффициент
скорости φ при несовершенном сжатии мало зависит от отношения n и его
находят по графику на рис.12.2, коэффициент сопротивления отверстия ξ можно найти из формулы, связывающей
Коэффициент
расхода μ1 = ε1 φ
, уравнение Бернулли записывается для сечения «1-1» в резервуаре и сечения в
наиболее сжатой части струи, где давление равно Р0 –атмосферному.
Выразим V1 через V2 V1S1=V2 ε1S0;
V1=V2 ε1S0/S1;
V1=V2 ε1n
.
(12.12)
Откуда получаем:
скорость для несовершенного
сжатия струи

расход для несовершенного
сжатия струи
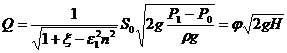
12.5. Истечение под
уровень
Истечением под
уровень называется истечение жидкости в пространство, заполненное этой же жидкостью
(рис. 12.12).
Вся кинетическая
энергия струи теряется на вихреобразование, как при внезапном расширении.
Составляя уравнение
Бернулли относительно свободных поверхностей «0 – 0» и «2 –
2» скорости считаем равными нулю, а приравнивая к
первой и второй части члены уранения для сжатого сечения получим с учетом
коффициента α :
или
1-я сумма, 2-я сумма, 3- сжатое сечение
где Н – обозначен
расчетный напор, ξ – коэффициент сопротивления отверстия, имеющий примерно
то же значение, что и при истечении в атмосферу, V – скорость истечения в сжатом сечении
струи.
Скорость в этом
случае
(12.15)
Расход
, (12.16)
где Sc – площадь
сжатого сечения струи, S0
– площадь отверстия.
Получились такие же расчетные формулы, что и при истечении в
воздух, только расчетный напор Н в данном
случае представляет собой разность
гидростатических напоров по обе стороны стенки, т.е. скорость и расход
не зависят от высоты расположения
отверстия.
Коэффициенты
сжатия и расхода при истечении под уровень можно принимать те же, что и при истечении в воздушную среду.
12.6.
Истечение через насадки при постоянном напоре.
Внешним
цилиндрическим насадком называется короткая трубка длиной, равной l = (2÷6)d без
закругления входной кромки (рис.12.4а). Истечение через такой насадок в атмосферу может
происходить в двух режимах.
12.5.1.Первый режим течения- безотрывный:
струя после входа в насадок сжимается
примерно как при истечении через
отверстие в тонкой стенке.
Затем сжатая часть
струи расширяется до размеров отверстия, и из насадка выходит полным сечением. Такой
режим истечения называют безотрывным. На выходе диаметр струи равен диаметру отверстия.
Для маловязких
жидкостей средние значения коэффициентов
для этого режима при больших числах Re равны: μ=φ = 0,8, ξ = 0,5-0,63.
Коэффициент μ
расхода такого насадка при этом режиме истечения жидкости зависит от относительной
длины насадка l/d и числа Re. Однако и при достаточном значении
l/d не всегда возможен
этот режим.
Пусть
истечение жидкости происходит под действием давления Р0 в среду
газа с давлением Р2. Расчетный напор в этом случае
H = (P0 – Р2)/(ρg)
В
струе на выходе из насадка давление равно Р2, в суженном месте
струи внутри насадка, где скорость увеличена, давление Р1 меньше, чем
Р2.
Чем больше напор, под которым происходит истечение и расход через насадок, тем
меньше абсолютное давление Р1.
Разность давлений Р2 – Р1
растет пропорционально напору Н.
Покажем
это, составив уравнение Бернулли для сечений 1 – 1 и 2 – 2,α = 1 (см. рис.12.4а):
Последний
член уравнения представляет собой потерю напора на расширение потока, которое в
данном случае происходит примерно так же, как и при внезапном расширении трубы (формула
Борда). Сжатие струи внутри насадка можно оценить коэффициентом сжатия ε,
как и в случае отверстия, поэтому на основании уравнения расхода
ε=S1/S2; V1S1=V2S2;
V1/V2=S2/S1=1/ ε;
V1=V2/ε. (12.17)
Заменив
с помощью этого соотношения скорость V1 в уравнении
Бернулли на скорость V2, а ее скорость V2 выражением через , найдем падение давления внутри насадка:
(12.18)
Подставляя сюда φ = 0,8 и
ε=0.63, получаем
(Р2 – Р1 ) ≈ 0,75ρgH (12.19)
Если
истечение происходит в среду, где Р2 равно постоянному ,
например, атмосферному давлению, увеличение
напора до критической величины Нкр приводит
к уменьшению Р1 – абсолютное давление в сжатом сечение «1 – 1» внутри насадка может уменьшиться до давления насыщенных паров. Поэтому существует
величина напора, называемая критическим
напором
Hкр ≈ Р2 /(0,75ρg). (12.20)
Следовательно,
при Н
> Hкр
давление Р1 должно
стать отрицательным, но отрицательных давлений в жидкости не бывает, поэтому
первый режим истечения при
Н
> Hкр
делается невозможным. При Н ≈ Hкр происходит внезапное
изменение режима истечения, переход от первого режима ко второму (см. рис.12.4в).
12.5.2. Второй режим истечения
характеризуется тем, что струя после сжатия уже не расширяется, сохраня
цилиндрическую форму, и перемещается внутри насадка, не соприкасаясь с его
стенками. Течение становится таким же, как из отверстия в тонкой стенке, с теми
же значениями коэффициентов. Следовательно, при переходе от первого режима ко
второму скорость возрастает, расход
уменьшается, благодаря сжатию струи.
Если
через насадок происходит истечение воды в атмосферу, то
Hкр ≈ Ра /(0,75ρg) = 10,33/0,75 ≈ 14 м.
Когда
давление Рн.п.
насыщенных паров истекающей жидкости соизмеримо с давлением Р2
среды, в которую происходит истечение,
пренебречь величиной Рн.п. нельзя, в формуле (12.19) следует принять Р1
= Рн.п.
Hкр = (Ра – Рн.п.)
/(0,75ρg) (12.21)
Если
после перехода от первого режима истечения ко второму уменьшить напор Н,
то второй режим будет сохраняться вплоть до самых малых Н. Это значит, что второй
режим истечения возможен при любых напорах, следовательно, при Н < Нкр возможны оба
режима.
При
истечении через цилиндрический насадок под уровень первый режим истечения не
будет отличаться от описанного выше. Но когда абсолютное давление внутри
насадка благодаря увеличению Н падает до давления насыщенных
паров перехода ко второму режиму не происходит, а начинается кавитационный
режим, при котором расход перестает зависеть от противодавления Р2,
получается эффект стабилизации расхода. При этом чем меньше относительное противодавление
Р2/Р0
= Рвых/Рвх =, которое является критерием кавитации, тем шире
область кавитации внутри насадка и тем меньше коэффициент расхода μ.
Таким
образом, при истечении жидкости через внешний цилиндрический насадок под
уровень коэффициент является функцией трех безразмерных критериев, а именно
μ = f (l/d, Re, ).
Результаты
новых экспериментальных исследований этого случаи истечения представлены в
безразмерных координатах на рис. 1.85. На рис.1.85а даны зависимости от Re при l/d = 3
для ряда значений , начиная от
= 0 и до
>
, где
– критическое
значение , соответствующее началу кавитации и, следовательно,
критерию ηкр(см. п. 1.23). На рис. 1.85б показаны области кавитационных и
безкавитационных режимов истечения через насадки с l/d = 3; 5 и 10. Увеличениепри возрастании Re объясняется уменьшением коэффициента ε сжатия струи
внутри насадка, т. е. увеличением степени сжатия, а уменьшение при увеличении l/d происходит из-за возрастания давления в сжатом сечении вследствие
увеличения потерь на трение по длине насадка.
Таким
образом, внешний цилиндрический насадок имеет существенные недостатки: на
первом режиме – большое сопротивление и недостаточно высокий коэффициент расхода,
а на втором – очень низкий коэффициент расхода. Недостатком является также двойст-венность
режима истечения в газовую среду при Н < Нкр, а следовательно двузначность
расхода при данном Н и возможность кавитации при истечении под уровень.
При
использовании цилиндрического насадка (сверления в толстой стенке), например в
качество жиклеров, дросселей или форсунок эти недостатки следует учитывать или
улучшать насадок.
Внешний
цилиндрический насадок может быть значительно улучшен путем закругления входной
кромки (см. штриховые линии на рис. 1.83) или устройства конического входа с
углом конусности около 60° (см. жиклер на рис. 1.75).
Чем
больше радиус закругления, тем выше коэффициент расхода и ниже коэффициент
сопротивления. В пределе при радиусе кривизны, равном толщине стенки, цилиндрический
насадок приближается к коноидальному насадку, или соплу.
Коноидальный
насадок (рис. 1.86) очерчивается приблизительно по форме естественно сжимающейся
струи и, благодаря этому, обеспечивает безотрывность течения внутри насадка в
параллельноструйность в выходном сечении. Это весьма распространеный насадок, так
как он имеет коэффициент расхода, близкий к единице, и очень малые потери
(коэффициент сжатия ε = 1), а также устойчивый режим течения без кавитации.
Значения
коэффициента сопротивления те же, что и при плавном сужении (см. п. 1.32), т.
е. ξ= 0,03 ÷ 0,1 (большим Re соответствуют малые ξ ‚ и наоборот). В соответствии с этим
μ =φ= 0,99÷0,96.
Диффузорный
насадок представляет собой комбинацию сопла и диффузора (рис. 1.87).
Приставка
диффузора к соплу влечет за собой снижение давления в узком месте насадка, а
следовательно, увеличение скорости и расхода жидкости через него. При том жедиаметре
узкого сечения, что и у сопла, и том же напоре диффузорный насадок может дать
значительно больший расход (увеличение до 2,5 раза), чем сопло.
Такие насадки
применяют в том случае, когда заданы диаметр узкого сечения и напор и требуется
получить возможно больший расход. Однако, использовать диффузорных насадков
можно лишь при небольших напорах Н = 1 ÷4
м, так как иначе в узком месте насадка возникает кавитация. Следствием кавитации являются увеличение
сопротивления и уменьшение пропускной способности насадка.
На рис.1.88
показано падение коэффициента расхода диффузорного насадка с увеличением напора
вследствие кавитации, возникающей в узком месте насадка при истечении воды в атмосферу.
Коэффициент
расхода отнесен к площади узкого сечения, т. е. . Приведенная кривая получена в результате испытания диффузорного
насадка, обладающего наивыгоднейшим углом и степенью расширения, которые
обеспечивают наибольший коэффициент расхода.
Внутренний
цилиндрический насадок или насадок Борда, изображен на рис.1.89. Там же
схематически показаны два режима истечения , аналогичные режимам истечения
через внешний цилиндрический насадок. Очертания струи при первом режиме
показаны сплошными линиями, а при втором – штриховыми. Так как частицы жидкости
приближаются к входному отверстию
насадка из всего прилежащего объема, а некоторые из них, попадающие на
периферию струи, изменяют направление своего движения на 180°, то степень
сжатия струи в данном насадке больше, а коэффициент ε меньше, чем во внешнем
цилиндрическом насадке. Значение ε в этом случае при истечении идеальной
жидкости может быть получено на основании
теоремы Эйлера об изменения количества движения (см. п. 1.15). Применим эту
теорему к фиксированному объему в виде кругового цилиндра ABCD соосного с насадком, и с основанием
CD, достаточно удаленным от насадка, где V=0. Пренебрегая толщиной стенки
насадка на основании указанной теоремы при втором режиме истечения получим
PS0 = ρSс*V2,
где
P— давление в центре
основания CD, S0 и Sс —
площади отверстия насадка и сечения струи (силы давления жидкости на кольцевые
площади оснований цилиндра ABCD уравновешиваются, а избыточное
давление по площади S0 в
плоскости АВ равно нулю.
С
другой стороны, для скорости истечения имеем
1 .
IIосле
подстановки второго уравнения в первое и сокращения на Р и ρ получим
ε = Sс / S0 = ½.
Этому
значению ε соответствуют значения коэффициентов расхода μ = 0,71 и потерь
ξ =1, что подтверждается опытами при первом режиме истечения и больших
числах Рейнольдса.