На рисунке 12.27 изображена древняя китайская головоломка “Танграм”.
1) Вырежите из бумаги квадрат со стороной 8 см и разрежьте его на фигуры танграма. Назовите все семь фигур. Есть ли среди них равные? Найдите площадь каждой фигуры. Назовите равновеликие фигуры.
2) Составьте:
а) треугольник из двух, трех, пяти и семи частей танграма;
б) квадрат из двух и трех частей танграма;
в) прямоугольник из трех, четырех и семи частей танграма.
3) Из каких частей тагнрама можно составить:
а) две равные фигуры;
б) две равновеликие фигуры;
в) прямоугольник, равновеликий треугольнику 7?


reshalka.com
ГДЗ учебник по математике 6 класс Дорофеев. 12.2 Площади. Номер №1027
Решение 1

фигура 1 − равнобедренный прямоугольный треугольник;
фигура 2 − равнобедренный прямоугольный треугольник;
фигура 3 − равнобедренный прямоугольный треугольник;
фигура 4 − квадрат;
фигура 5 − равнобедренный прямоугольный треугольник;
фигура 6 − параллелограмм;
фигура 7 − равнобедренный прямоугольный треугольник.
Равные фигуры:
1 = 2;
3 = 4.
1) 8 * 8 : 4 = 64 : 4 = 16
(
с
м
2
)
− площадь первой и второй фигуры;
2) 4 * 2 : 2 = 8 : 2 = 4
(
с
м
2
)
− площадь третьей и пятой фигуры;
3) 4 * 2 = 8
(
с
м
2
)
− площадь четвертой фигуры;
4) 4 * 2 = 8
(
с
м
2
)
− площадь шестой фигуры;
5) 4 * 4 : 2 = 16 : 2 = 8
(
с
м
2
)
− площадь седьмой фигуры.
Равновеликие фигуры:
1 и 2;
3 и 5;
4, 6 и 7.
Решение 2
а)
Из двух частей:

Из трех частей:

Из пяти частей:

Из семи частей:

б)
Из двух частей:

Из трех частей:
в)
Из трех частей:

Из четырех частей:

Из семи частей:

Решение 3
а) две равные фигуры можно сложить из фигур:
3 и 5;
4 и 7.
б) две равновеликие фигуры можно сложить из фигур:
3 и 5 они будут равновелики фигуре 4, а также фигуре фигуре 6;
в) из фигур 3 и 5 можно составить прямоугольник, равновеликий треугольнику 7.
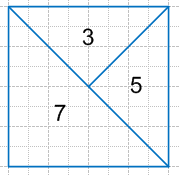
Найти площадь части танграма с вопросом
CreativeMan
Ученик
(207),
на голосовании
2 года назад
Пожалуйста помогите. У нас математичка придумала задание, так чтобы мы не поняли как это решать. Может вы поймёте?
Голосование за лучший ответ
Наталия Тузина
Мудрец
(17270)
2 года назад
a – сторона квадрата
100 – площадь 14 квадрата =>
a*a 4 = 100 ——-> a^2 = 400 ——-> a = 20
(?) – треугольник со сторонами а2 и а4 =>
(?) = 12 * a2 * a4 = a^2 16 = 40016 = 25
Хотя сразу видно, что (?) составляет 14 от треугольника (100)

Параллелограмм
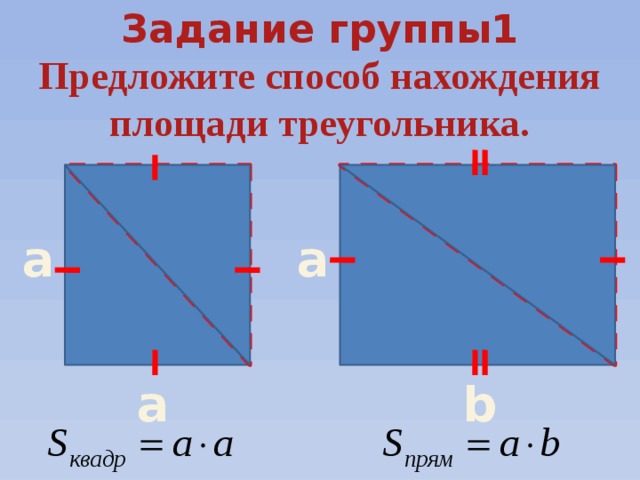
Задание группы1
Предложите способ нахождения площади треугольника.
a
a
b
a

Задание группы2
Предложите способ нахождения
площади закрашенной фигуры
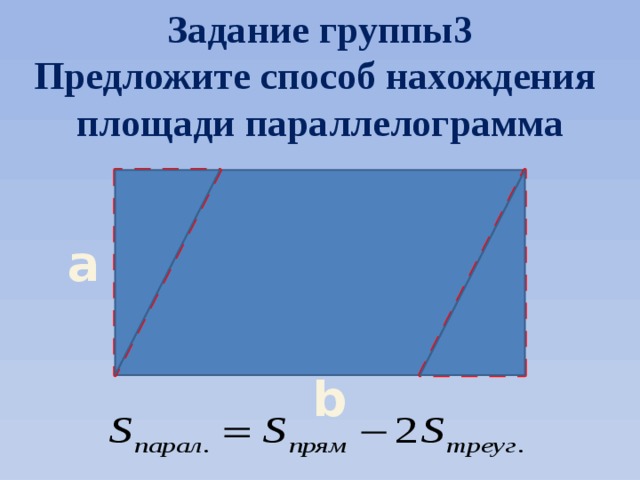
Задание группы3
Предложите способ нахождения
площади параллелограмма
a
b
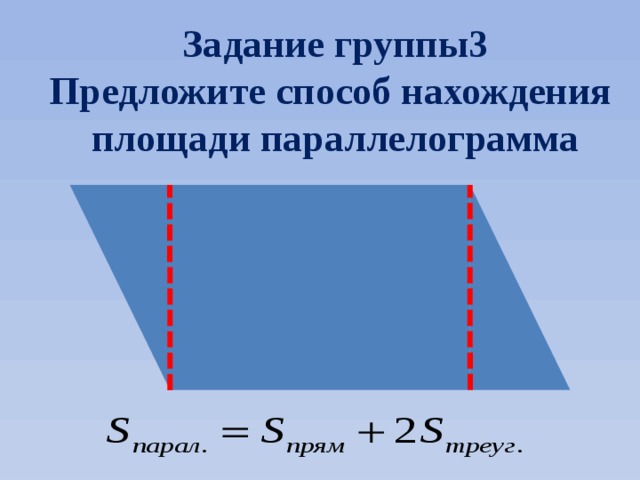
Задание группы3
Предложите способ нахождения
площади параллелограмма

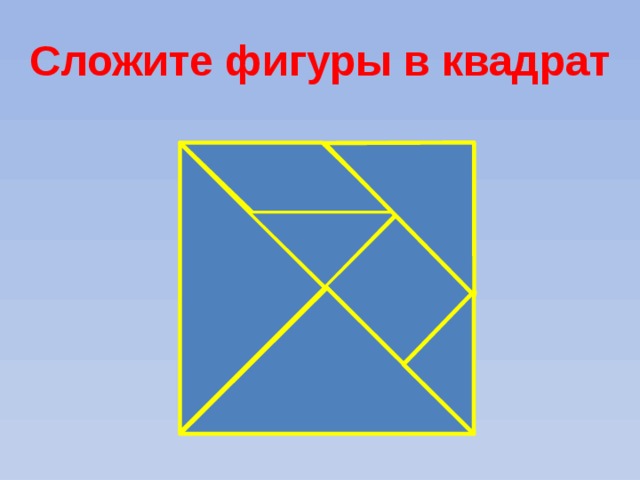
Сложите фигуры в квадрат


Автор ответа: dvoeglazov1232
10
Умножай шесть на шесть и получишь свой ответ, так как площадь квадрата находиться так Sкв=а*а
bobby66:
Так ведь требуется найти площадь каждой части…
Бирский филиал Федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Башкирский государственный университет»
Уфимский государственный авиационный технический университет
Муниципальное казенное учреждение Управление образования
муниципального района Бирский район Республики Башкортостан
Муниципальное бюджетное общеобразовательное учреждение Лицей г. Бирска
муниципального района Бирский район Республики Башкортостан
Всероссийская научно-практическая конференция
школьников общеобразовательных учреждений,
студентов ВУЗов и СПО
ПОИСК
(Познание
Открытие
Исследование
Совершенствование
Креатив)
Секция: «Математика»
Исследовательская работа на тему:
«Танграм»
Выполнила: Саркиева Лилия Болеславовна
обучающаяся 5 В класса
МБОУ Лицей №1 с. Мишкино
им. Флорида Булякова
Научный руководитель: Алексеева Гузель Фанавиевна
учитель математики
МБОУ Лицей №1 с. Мишкино
им. Флорида Булякова
Бирск 2017
Содержание.
Введение
1. Определение головоломки…………………………………………..…стр.4
1.1. Виды головоломок…………………………………………………….стр.4
1.2. Пазлы…………………………………………………………………..стр.4
1.3. Что такое «Танграм»?…………………………………………………………………стр.4
1.4. Как изготовить Танграм?…………………………………………………………..стр.5
2. О названии «Танграм»………………………………………………….стр.6
2.1. Легенда первая………………………………………………………..стр.6
2.2. Легенда вторая………………………………………………………..стр.7
2.3. Легенда третья………………………………………………………..стр.7
2.4. Знаменитые люди и «Танграм»…………………….……………….стр.8
2.5.Площадь и свойства площадей с использованием «Танграм»…….стр.9
3. Применение «Танграма»…………………………………………….стр.10
3.1. Правила игры………………………………………………………..стр.11
3.2. Как играть…………………………………………………………….стр.11
4. Практическая часть……………………………………………………стр.12
Заключение
Литература
Приложения
Введение
Актуальность выбранной темы:
Головоломки – игрушки на все времена. С самых давних пор умельцы изготавливали подобные забавы, отличающиеся многообразием вариантов решения. До появления компьютерных и бурного развития настольных игр, одним из основных развлечений для большинства людей была игра – головоломка “Танграм”. В наше время тоже очень много людей, которые увлекаются головоломками. Они любимы не только детьми, но и взрослыми. Это способ развлечения и возможность развития логического мышления и геометрической интуиции.
Летом на витрине магазина я увидела красивую коробочку, на которой было написано «Танграм».
Мне стало интересно:
– где и в каком веке зародилась эта игра?
– можно ли самому сделать «Танграм», и какие материалы для этого подойдут?
– как с помощью семи геометрических фигур можно составлять всевозможные фигуры?
– пригодится ли мне изучение «Танграма» в обучении?
Теперь мне необходимо ответить на все эти вопросы.
Объект исследования: информационные источники, позволяющие проследить историю возникновения «Танграма» и сферу применения этой игры.
Предметом исследования: «квадрат – Танграм», состоящий из семи геометрических фигур.
Гипотеза исследования: Я предположила, что эта старинная головоломка поможет мне при изучении математики.
Цель исследования: изучение истории возникновения головоломки «Танграм» и сферы ее применения.
В ходе достижения цели мне потребуется решить следующие задачи:
-
Проследить историю возникновения игры «Танграм».
-
Выяснить, из какого материала лучше всего изготовить эту головоломку.
-
Научиться изображать силуэты животных, людей и других предметов.
-
Изготовить для домашней коллекции новую развивающую игру.
-
Узнать сферу применения «Танграма».
Методы исследования:
Теоретические: изучение материалов по теме исследование; анализ и обобщение собранной информации; моделирование; конструирование; классификация.
Эмпирические: наблюдение и сравнение.
Этапы работы над проектом
-
Подготовительный
-
Обоснование актуальности выбранной темы, определение объекта и предмета исследования.
-
Поиск материала по истории создания «Танграма».
-
Изучение правил геометрического конструктора.
-
Сбор материалов о сфере применения «Танграма».
-
Подбор материалов для изготовления головоломки.
Вывод: на данном этапе я подобрала много интересного материала и определилась с формой и внешним видом «Танграма» для домашней коллекции настольных игр.
-
Практический
-
Училась составлять разнообразные фигуры с помощью геометрического конструктора
-
Изготовила «Танграм» из фанеры с учителем технологии.
-
Сделала подборку наиболее интересных изображений животных, птиц, людей и оформил книжку с заданиями и ответами для головоломки.
-
Узнала, что между семью танами существует ряд геометрических соотношений.
-
Узнала о практическом применении этой головоломки.
Вывод: на данном этапе я нашла и изучила геометрические сведения, которые несомненно будут полезны мне при изучении геометрии в дальнейшем. Таким образом, я подтвердила свою гипотезу.
-
Обобщающий
-
Анализ своей деятельности.
-
Подготовка презентации.
-
Представление продукта и результатов работы на ученической конференции.
-
Знакомство своих друзей с новой настольной игрой.
Вывод: Я научилась планировать свою работу, выбирать нужную информацию и познакомила своих друзей с новой интересной игрой.
-
Определение головоломки.
Головоломка — непростая задача, для решения которой, как правило, требуется сообразительность, а не специальные знания высокого уровня.
-
Виды головоломок.
Виды головоломок: общепринятая классификация головоломок отсутствует, можно лишь условно разделить их на несколько групп:
Устные головоломки – задачи, полное условие которых может быть сообщено в устной форме не требующие для решения привлечения никаких дополнительных предметов (загадки, шарады)
Головоломки с предметами логические задачи с обычными бытовыми предметами (спичками, монетами, карточные головоломки).
Печатные головоломки напечатанные или нарисованные “картинки”, в которых надо нарисовать какие-то символы по определенным правилам (кроссворды, ребусы).
Механические головоломки предметы, специально изготовленные как головоломки (кубик Рубика, змейка Рубика, пазлы, танграм).
-
Пазлы.
Игрой внешне близкой танграму являются пазлы. В начале пазлы являлись большим набором фигур неправильной формы из которых необходимо было сложить картинку — задание. Несмотря на эту схожесть — танграм, задача противоположная, так как семь базовых элементов позволяет значительное множество фигур, а в случае пазла мы ограничены только одним решением. Сравнительный анализ танграма с другими аналогичными играми был сделан Р.Ридом в книге «Танграмы: 330 головоломок». Для игры танграм основным требованием к человеку является логическое мышление и геометрическая интуиция, а для игры пазл — все-таки всего лишь усидчивость и терпение.
-
Что такое «Танграм»?
Танграм (от китайского «семь дощечек мастерства») — головоломка, состоящая из семи танов (плоских геометрических фигур), полученных делением квадрата на семь частей – 2 больших, 2 маленьких и 1 средний треугольник, 1 малый квадрат и параллелограмм, которые складывают определённым образом для получения другой, более сложной, фигуры (изображающей человека, животное, предмет домашнего обихода, букву или цифру и т. д.).
Фигура, которую необходимо получить, при этом обычно задаётся в виде силуэта или внешнего контура. 
При решении головоломки требуется соблюдать два условия: первое — необходимо использовать все семь фигур танграма, и второе — фигуры не должны перекрываться между собой.
-
Как изготовить танграм.
Базовым элементом танграма является тан. Изготовить «Танграм» можно из картона. В квадрате чертим диагональ – получается 2 треугольника. Один из них разрезаем пополам на 2 небольших треугольника. Отмечаем на каждой стороне второго большого треугольника середину. Отсекаем по этим отметкам средний треугольник и остальные фигуры.
Более практичный и долговечный «Танграм» можно вырезать из жесткой офисной папки или пластиковой коробки из под DVD. Можно немного усложнить себе задачу, вырезав «Танграм» из кусочков разного фетра, ткани, обметав их по краям, или вовсе из фанеры или дерева.


-
О названии «Танграм».
Установить точное происхождение этого названия невозможно. Согласно одной версии, его дали головоломке люди, жившие на берегах реки Танка в Китае. Они были известными купцами. Моряки из стран Запада, побывавшие в китайских портах, вероятно, научились играть в танграм, общаясь с местными жителями, а затем привезли головоломку на родину.
Согласно другой версии, это название произошло от старого английского слова «tangram», означавшего «головоломка». В 1903 г. Сэм Лойд подробно описал происхождение танграма. Семь фигур танграма ассоциировали с Луной, Марсом, Меркурием, Юпитером, Венерой, Сатурном и Солнцем – с семью небесными телами, известными с глубокой древности и давшими название дням недели. В своей книге Сэм Лойд представил 652 фигуры, которые можно сложить из деталей танграма. Некоторые фигуры были заимствованы из китайских книг, другие он изобрел сам.
Самое раннее издание, в котором были представлены фигуры из танграма, появилось в Китае в 1813 г., хотя сохранились только упоминания о нем в более поздних публикациях 1815 г.
В то время танграм как увлекательная игра уже пользовалась огромной популярностью.
В начале ХIX века игра быстро распространилась по Европе и Америке в результате торговых отношений с Китаем. Рынок наводнили издания и настольные игры с фигурами танграма. В Англии, Франции, Италии, Германии, Голландии, Дании, Швеции, Швейцарии и Австрии головоломка становилась все популярнее и популярнее. Такие выдающиеся личности, как Льюис Кэрролл и Эдгар Аллан По, не скрывали своего пристрастия к ней.
Легенда первая: версия про разбитую плитку.
Более 4000 тысяч лет назад у одного человека из рук выпала фарфоровая плитка и разбилась на семь частей. Расстроенный, он в спешке старался ее сложить, но каждый раз получал все новые интересные изображения. Это занятие оказалось настолько увлекательным, что впоследствии квадрат, составленный из семи геометрических фигур, назвали Доской Мудрости.
Легенда вторая: три мудреца придумали «Ши-Чао-Тю».
Появление этой китайской головоломки связано с красивой легендой. Почти две с половиной тысячи лет тому назад у немолодого императора Китая родился долгожданный сын и наследник. Шли годы. Мальчик рос здоровым и сообразительным не по летам. Одно беспокоило старого императора: его сын, будущий властелин огромной страны, не хотел учиться. Мальчику доставляло большее удовольствие целый день забавляться игрушками. Император призвал к себе трех мудрецов, один из которых был известен как математик, другой прославился как художник, а третий был знаменитым философом, и повелел им придумать игру, забавляясь которой, его сын постиг бы начала математики, научился смотреть на окружающий мир пристальными глазами художника, стал бы терпеливым, как истинный философ, и понял бы, что зачастую сложные вещи состоят из простых вещей. Три мудреца придумали “Ши-Чао-Тю”- квадрат, разрезанный на семь частей.
Легенда третья: семь книг Тана.
Более 4000 лет назад в Китае были составлены семь книг о танграмах, каждая из которых насчитывает ровно тысячу фигур.
Согласно легенде Лойда, Тан был легендарным китайским мудрецом, которому его соотечественники поклонялись как божеству.
Фигуры в своих семи книгах он расположил в соответствии с семью стадиями в эволюции Земли. Его танграмы начинаются с символических изображений хаоса и принципа «Инь» и «Ян». Затем следуют простейшие формы жизни, по мере продвижения по древу эволюции появляются фигуры рыб, птиц, животных и человека. По пути в различных местах попадаются изображения того, что создано человеком: орудия труда, мебель, одежда и архитектурные сооружения.
Одна из «известных» китайскх пословиц: «Только глупец взялся бы написать восьмую книгу Тана».
2.4. Знаменитые люди и «Танграм»
Льюис Кэрролл.
Все мы хорошо знаем книгу «Алиса в стране чудес» Л.Кэрролла (Чарльз Лютвидж Доджсон). Однако это его не единственное произведение. В книге «Модная китайская головоломка» он пишет, что танграм был любимой игрой Наполеона, который, лишившись трона, в изгнании проводил долгие часы за этой забавой, «упражняя свое терпение и находчивость». Упоминание о любимой игре Наполеона, скорее всего не соответствует действительности, однако, и нет обратных доказательств, что, в свою очередь, позволяет существовать и такой красивой версии.
Эдгар А. По.
Одним из поклонников игры был Эдгар А. По. Принадлежавший ему танграм сделан из слоновой кости и в настоящее время хранится в Нью-Йоркской публичной библиотеке.
Роберт ван Гулик.
Известный писатель и дипломат Роберт ван Гулик в романе «Убивающие ногтями» построил весь сюжет книги вокруг танграма.
Абдул-Вефа.
Одним из первых научных трудов известных человечеству по решению задач на разрезание является трактат Абдул Вефа. Он являлся персидским астрономом. Жил в десятом веке в Багдаде. Сохранились лишь отдельные части этой книги и в том числе решение задачи как разрезать три одинаковых квадрата на 9 частей, из которых в дальнейшем, возможно, сложить один большой квадрат. В дальнейшем решение этой задачи с условием использования минимального количества элементов было сделано англичанином Генри Э. Дьюдени. Он решил задачу Абдул Вефа с использованием 6 элементов, и это является минимальным решением на настоящее время.
Гарри Линдгрен.
Энциклопедией решения различных задач на разрезание является книга Гарри Линдгрена «Геометрия разрезаний». В этой книге можно найти рекорды по разрезанию многоугольников на заданные фигуры. При использовании треугольника как базового элемента — многоугольники можно разрезать на следующие количество частей:
квадрат — 4, пятиугольник — 6, шестиугольник — 5, семиугольник — 9, восьмиугольник — 8, девятиугольник — 9, десятиугольник — 8
двенадцатиугольник — 8.
2.5.Площадь и свойства площадей с использованием «Танграма».
Изучая тему в 5 классе «Площадь. Свойства площадей». Можно чётко проследить данное понятие на примере «Танграма». Собрав квадрат, становиться ясно, что измерение части занимаемой той или иной фигурой, удобно осуществлять квадратом, с заданной единицей длины стороны квадрата. 
Свойства площадей:
1.Равные фигуры имеют равные площади. С помощью наложения треугольников в танграме это хорошо просматривается. Треугольник аbd = треугольнику adh. Треугольник hfi= треугольнику dgc.
2.Чтобы найти площадь сложной фигуры надо найти сумму всех площадей входящих в неё фигур.
В танграме, площадь фигуры cbeg=площадь треугольника cgd+ площадь треугольника hti, а так как площади этих треугольников равны, то площадь четырёхугольника cbeg=2 площадям треугольника cgd. Площадь треугольника iej=2площадям cgd. Таким образом площадь четырёхугольника cbeg=площади треугольника iej.
Вывод: Действительно тема площадей и свойств площадей прекрасно иллюстрируется танграмом.
-
Применение «Танграм».
Сфера применения «Танграма» гораздо шире, чем просто игра. Из частей головоломки можно составлять изученные геометрические фигуры (треугольник, квадрат, параллелограмм, трапеция, прямоугольник), вычислять их площади, а также сравнивать эти фигуры с помощью наложения.
В 1942 г. китайские математики показали, что из одних только деталей танграма можно сложить 13 выпуклых фигур, которые представлены ниже.

А еще между деталями танграма существует ряд геометрических соотношений.
Соотношение площадей:
-
Площадь большого треугольника вдвое больше площади среднего треугольника.
-
Средний треугольник, квадрат и параллелограмм имеют одинаковую площадь.
-
Площадь среднего треугольника вдвое больше площади маленького треугольника.
Соотношение между сторонами и углами дают возможность строить из деталей танграма различные фигуры, приставляя детали друг к другу. Всего насчитывают более 7 000 различных комбинаций.
Сфера применения «Танграма» гораздо шире, чем просто игра: его можно встретить в дизайне одежды, архитектуре и ландшафтном дизайне. Самое удачное применение танграма, пожалуй в качестве мебели. Есть и столы танграмы и трансформируемая мягкая мебель и знаменитые настенные полки фирмы Lago.
Вся мебель построенная по принципу танграма очень удобна и функциональна. Каждый раз она может видоизменятся в зависимости от настроения и желания хозяина. Интересный вариант трансформируемых диванов дизайнера Julien Bernard. Эта модель была представленна на выставке в Милане в 2009 году.
Самая известная коллекция мебели в стиле танграм у дизайнеров по интерьерам – конечно, Lago. Сколько всевозможных вариантов и комбинаций можно составить из этих симпатичных полочек. Сами производители выпустили вместе с инструкцией по сборке несколько страниц с идеями для библиотеки, гостиной, спальни и детской.
-
Правила игры:
Классические правила танграма очень просты. Игра заключается в сложении из деталей головоломки геометрических фигур, букв, циыр, силуэтов животных, растений, людей, предметов – всего, что подскажет фантазия.
-
В каждую собранную фигуру должны входить все семь элементов.
-
При составлении фигур элементы не должны налегать друг на друга.
-
Элементы фигур должны соприкасаться друг с другом.
-
Начинать нужно с того, чтобы найти место самого большого треугольника.
В результате игры получается плоскостное силуэтное изображение. Оно условно, схематично, но образ легко угадывается по основным характерным признакам предмета: его строению, пропорциональному соотношению частей и форме.
-
Как играть?
Каждая фигура игры должна складываться из семи частей танграма, и при этом они не должны перекрываться. Самый легкий вариант – собирать фигуры по расчерченным на элементы схемам (ответам), как мозаику.
Немного практики, и можно научиться составлять фигуры по образцу-контуру и даже придумывать свои фигуры по такому же принципу.
4. Практическая часть.
Я провела опрос среди пятиклассников:
1.Любишь ли ты решать головоломки?
2. Часто ли ты решаешь головоломки?
3. Знаком ли ты с игрой «Танграм»?
Результаты опроса выглядят так:
По результатам опроса видно, что большинство учеников любит головоломки, но мало кто знает про игру «Танграм». Все хотят познакомиться с этой игрой, поиграть в нее.
Поэтому мной было проведено занятие математического кружка, на котором я познакомила своих одноклассников с игрой «Танграм».
Мы решили попробовать сконструировать собственные фигуры из танграма и провели в школе с ребятами 5 классов эксперимент «Проверь свои возможности». В эксперименте приняли участие 60 учащихся нашей школы. Нам было предоставлено 25 детских работ. В результате нам удалось оставить свой след в истории создания фигур из танграма.
Заключение.
Танграм – одна из удивительных головоломок, которой способен увлечься практически любой человек. Для математиков она служит неиссякаемым источником геометрических соотношений. Учителя используют танграм как наглядное пособие. Коллекционеры ценят танграмы из дерева и слоновой кости, а также исторические издания, посвященные богатым коллекциям фигур. Можно играть танграмом, детали которого вырезаны из листа бумаги, а для тех, кто признает только игры с клавиатурой и экраном, есть всевозможные компьютерные программы по танграмам.
В начале своей работы я предположила, что эта старинная головоломка поможет мне в учебе. Моя гипотеза подтвердилась, так как действительно с помощью «Танграм» я изучила полезные геометрические сведения.
Также дома у нас появилась интересная настольная игра. Эта элегантная старинная головоломка, удивляющая простотой деталей и многообразием фигур, которые можно из них составить, по-прежнему завораживает ценителей, каким бы ни был их возраст.
Мне кажется, что игры развивают детей, учат находить правильное решение, находить выход из трудной игровой ситуации. Игры не только занимают досуг, но и обучают.
Вообще, игры – головоломки – это хорошая разрядка от трудных ежедневных проблем и они просто интересны!
Литература:
1. И.Ф. Шарыгин, Л.Н. Ерганжиева: «Наглядная геометрия, 5-6 класс».
2. Г. К. Муравин, О. В. Муравина: «Математика, 5 класс».
3. http://ru.wikipedia.org/wiki/%D2%E0%ED%E3%F0%E0%EC
4. http://festival.1september.ru/articles/626772/
5. http://www.school61.ru/Science/2011/tangram/tangram1.htm
Приложение 1.
Работы учащихся 5 класса.












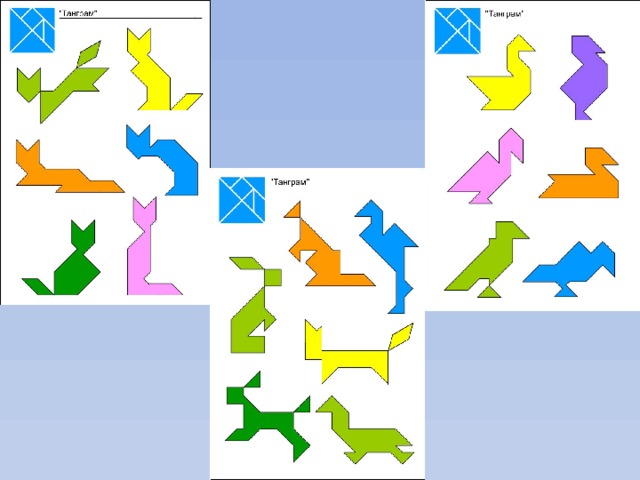
Приложение 2. Фигуры для игры.

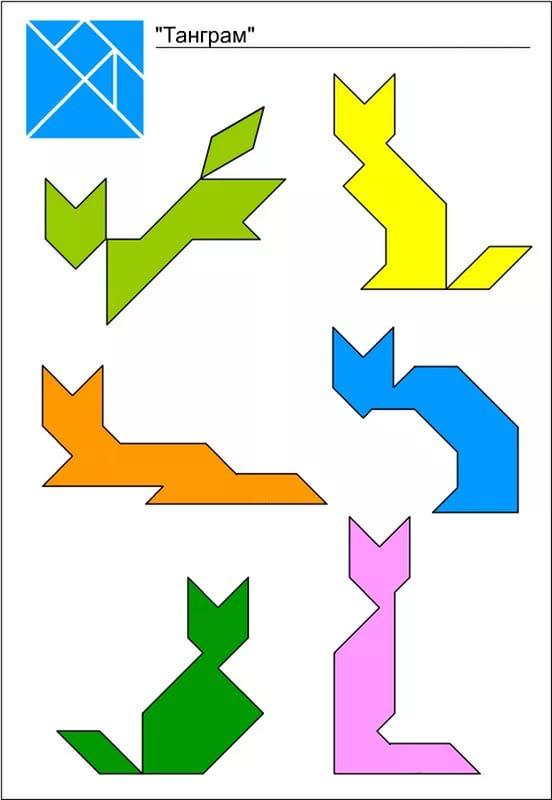

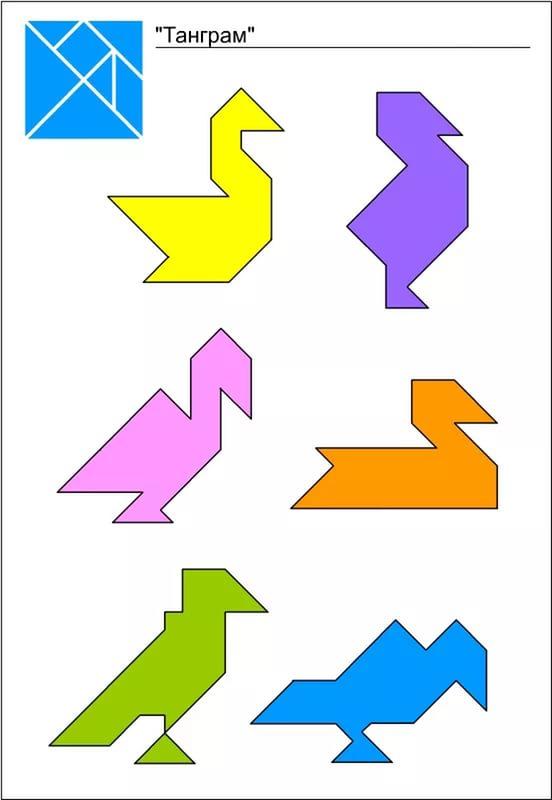
18
