Как найти площадь тени круга

Let $a$ be a side of the square. Consider the following diagram

The area we need to calculate is as follows.
$$begin{eqnarray} color{Black}{text{Black}}=(color{blue}{text{Blue}}+color{black}{text{Black}})-color{blue}{text{Blue}}. end{eqnarray}$$

Note that the blue area can be calculated as
$$begin{eqnarray}color{blue}{text{Blue}}=frac14a^2pi-2cdotleft(color{orange}{text{Yellow}}+color{red}{text{Red}}right).end{eqnarray}$$

We already know most of the lengths. What’s stopping us from calculating the black area is lack of known angles. Because of symmetry, almost any angle would do the trick.

It’s fairly easy to calculate angles of triangle $begin{eqnarray}color{orange}{triangle POA}end{eqnarray}$, if we use cosine rule.

$$begin{eqnarray}
|PA|^2&=&|AO|^2+|PO|^2-2cdot|AO|cdot|PO|cosangle POA\
a^2&=&frac{a^2}{4}+frac{2a^2}{4}-2cdotfrac a2cdotfrac{asqrt2}{2}cdotcosangle POA\
4a^2&=&3a^2-2a^2sqrt2cosangle POA\
1&=&-2sqrt2cosangle POA\
cosangle POA&=&-frac{1}{2sqrt2}=-frac{sqrt2}{4}.
end{eqnarray}$$

Now, because of symmetry, we have $angle POA=angle POB$, so $angle AOB=360^circ-2angle POA$. So the cosine of angle $angle AOB$ can be calculated as follows:
$$begin{eqnarray}
cosangle AOB&=&cos(360^circ-2angle POA)=cos(2pi-2angle POA)\
cosangle AOB&=&cos(-2angle POA)=cos(2angle POA)\
cosangle AOB&=&cos^2(angle POA)-sin^2(angle POA)\
cosangle AOB&=&cos^2(angle POA)-(1-cos^2(angle POA))\
cosangle AOB&=&2cos^2(angle POA)-1\
cosangle AOB&=&2cdotleft(-frac{sqrt2}{4}right)^2-1=-frac34\
end{eqnarray}$$

From this, we can easily calculate the sine of angle $angle AOB$, using Pythagorean identity.
$$ sinangle AOB=sqrt{1-frac9{16}}=sqrtfrac{16-9}{16}=frac{sqrt7}4 $$

Going this way, I believe it’s not hard to calculate other angles and use known trigonometry-like formulas for area. Then you can easily pack it together using the first equation with colors.

Потому что так получается при интегрировании вращающейся полуокружности.

Сфера получается, если полуокружность обернуть вокруг её диаметра на 2пи радиан. Соответственно площадь сферы можно представить как сумму площадей “полосочек”, описываемых каждой точкой (точнее, каждым бесконечно малым кксочком) этой полуокружности. По какому радиусу вращается каждая такая точка – известно. Какая поэтому будет длина описываемой её окружности и, стало быть, площадь соответствующей полоски – тоже не штука сосчитать.

И вот если аккуратно провести такое интегрирование, то и получится значение, вчетверо превышающее площадь центрального сечения сферы.

Можно и по-другому. Можно представить шар, заключённый в этой сфере, как “сумму” множества элементарных пирамид с общей вершиной, находящейся в центре сферы (совпадающей, ясное дело, с центром шара). У всех этих пирамид будет одна и та же высота, практически равная радиусу сферы и тем ближе к нему, чем меньше площадь основания каждой такой пирамидки. Объём каждой пирамидки равен 1/3 произведения её высоты на площадь основания. Соверщенно очевидно, что объём всех пирамидок, то есть объем шара, будет равен суммарной площади оснований пирамидок, то есть площади сферы, на одинаковую для всех высоту. В итоге получаем, что объём шара равен 1/3 произведения радиуса сферы на площадь поверхности сферы. Поскольку объём шара равен 4/3 пиR³ (это доказывается независимо – например, через теорему Ньютона-Симпсона, которую нам давали в обычной средней школе), то отсюда враз выползает, что площадь сферы равна 4пиR². Да и вообще поверхность тела вращения равна производной от объёма по радиусу – тупо продифференцируйте формулу объёма шара…

Тень горизонтальной окружности.

Тень
от горизонтальной окружности на
фронтальной
плоскости проекций изо­бразится
в виде эллипса, который явля­ется
результатом пересечения плоско­сти
обертывающей лучевой цилиндри­ческой
поверхностью.

Контур
тени может быть получен путем построения
теней ряда точек ок­ружности.

Тень
от окружности может быть
построена также с помощью по­строения
тени описанного квадрата, в которую
вписывается затем эллипс по восьми
точкам .

На
рис. 196, а
даны
две проекции горизонтальной
окружности.

Тень
опи­санного
квадрата представляет собой параллелограмм.

Его
стороны и диагона­ли — это тени прямых
частного поло­жения
(см. рис. 191).

В
параллелограмм вписывается
эллипс.

В
процессе графических построе­ний,
как и в данном примере (см. допол­нительную
схему), бывает необходимо делить
отрезок прямой в соотношении стороны
квадрата к его диагонали, рав­ном
0,707 (
0,7).

Тень
окружности на фасаде
может быть построена без пла­на,
так как тень одной из диагоналей
располагается
вертикально.

На
рис. 196,
б
приведено построение падающей
тени на фасаде от горизон­тальной
полуокружности.

Это
постро­ение довольно часто будет
применяться при
построении теней архитектурных деталей,
состоящих из различных по­верхностей
вращения.

Тень
полуок­ружности
также может быть построена без второй
проекции.

Тень
вертикальной окружности.

На
рис.
196,
в
построена
тень на плоскости V
от
вертикальной окружности, распо­ложенной
в профильной плоскости.

Од­на
из диагоналей описанного вокруг
ок­ружности
квадрата дает тень по гори­зонтали
b‘—d_v.

В

параллелограмм, кото­рый является
тенью описанного квадра­та,
вписывают эллипс по восьми точ­кам.

Вопросы:

1. Что является
   тенью точки на плоскость? На поверхность
   геометрического тела?

2. Как построить
   тень точки на плоскость проекций?

3. Как построить
   тень точки на плоскость общего положения?

4. Как построить
   тень точки на поверхность геометрического
   тела?

5. Как построить
   тень от прямой?

6. Как будет падать
   тень от прямой на перпендикулярную к
   ней плоскость проекций?

7. Как будет падать
   тень от прямой на параллельную плоскость?

8. Как построить
   тень от плоской фигуры?

9. Как будет падать
   тень от плоской фигуры на параллельную
   ей плоскость?

10. Как изобразится
    тень от горизонтальной окружности на
    фронтальную плоскость?

Тема 3.3 Тени геометрических тел.(2 часа)

План занятия:

1. Определение линии
   светораздела и собственных теней на
   поверхности геометрических тел.

2. Тень от призмы.

3. Тень от цилиндра.

4. Тень от конуса.

5. Тень от сферы.

6. .Способ
   обратных лучей

Пусть
некоторый многогранник (тетраэдр) SABC
освещен пучком
параллельных лучей (рис. 4.15), для которого
требуется построить собственную и
падающую тени.

Для
этой цели через каждую его вершину
проводим световые лучи параллельно
заданному направлению и находим точки
их пересечения с одной из плоскостей
проекций (Н).
Так будут найдены тени вер-шин
многогранника на плоскость Н.
Соединив их друг с другом, получим тень
проволочного каркаса многогранника.
Но нам задан не «каркас», а непрозрачное
тело, тенью которого должна быть
некоторая фигура. В рассматриваемом
примере контуром падающей тени будет
треугольник (AHТ BHТ
SHТ). Этот треугольник
представляет собой сечение лучевой
призмы плоскостью Н.
Так как часть тени оказалась на задней
полуплоскости Н,
то пришлось дополнительно определить
тень вершины S на
плоскости V.
Реальную тень соединяем с точками
перелома тени на оси ox.
Множество точек, общих для поверхности
лучевой призмы и заданного многогранника,
образует замкнутый контур, отделяющий
освещенную часть поверхности, – контур
собственной тени.
Любой точке К контура
собственной тени соответствует точка
КНТ на
контуре падающей тени.

С
ледовательно,
контур падающей тени
является тенью контура собственной.
По первому контуру легко определить и
второй. В нашем случае
контур AHТ BHТ SHТ AHТ
ограничивает падающую
тень, значит, ребра AB,
BS, и SA
будут отделять
освещенные грани тетраэдра от теневых,
т. е. контуром собственной тени является
замкнутая линия A-B-S-A.
Этот контур ограничивает грань ABS,
которая окажется освещенной, так как
она обращена к источнику света. Остальные
грани находятся в собственной тени.

Э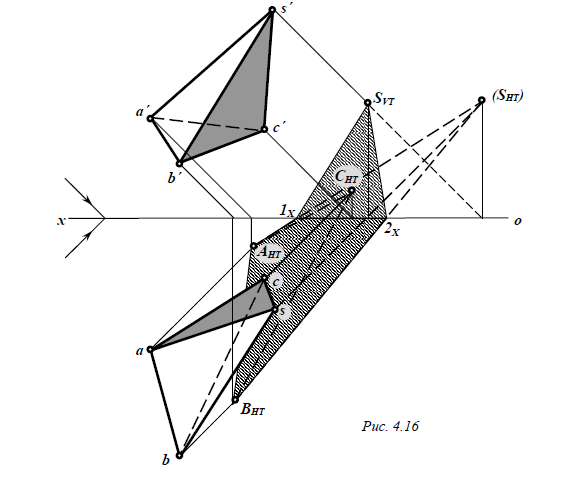
пюрное
решение данной задачи представлено на
рис. 4.16, где сначала построена тень
тетраэдра на Н,
а
затем с помощью реальной тени SVТ
найден
контур падающей тени на V.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #