Формулы площади геометрических фигур
Площадь геометрической фигуры – численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Формулы площади треугольника

-
Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты -
Формула площади треугольника по трем сторонам
Формула Герона
S = √p(p – a)(p – b)(p – c)
-
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними. -
Формула площади треугольника по трем сторонам и радиусу описанной окружности
-
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.где S – площадь треугольника,
a, b, c – длины сторон треугольника,
h – высота треугольника,
γ – угол между сторонами a и b,
r – радиус вписанной окружности,
R – радиус описанной окружности,p = a + b + c – полупериметр треугольника. 2
Формулы площади квадрата

-
Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.S = a2
-
Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.где S – площадь квадрата,
a – длина стороны квадрата,
d – длина диагонали квадрата.
Формула площади прямоугольника

Площадь прямоугольника равна произведению длин двух его смежных сторон
S = a · b
где S – Площадь прямоугольника,
a, b – длины сторон прямоугольника.
Формулы площади параллелограмма

-
Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.S = a · h
-
Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.S = a · b · sin α
-
Формула площади параллелограмма по двум диагоналям и углу между ними
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.где S – Площадь параллелограмма,
a, b – длины сторон параллелограмма,
h – длина высоты параллелограмма,
d1, d2 – длины диагоналей параллелограмма,
α – угол между сторонами параллелограмма,
γ – угол между диагоналями параллелограмма.
Формулы площади ромба

-
Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.S = a · h
-
Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.S = a2 · sin α
-
Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.где S – Площадь ромба,
a – длина стороны ромба,
h – длина высоты ромба,
α – угол между сторонами ромба,
d1, d2 – длины диагоналей.
Формулы площади трапеции

-
Формула Герона для трапеции
S = a + b √(p-a)(p-b)(p-a-c)(p-a-d) |a – b| -
Формула площади трапеции по длине основ и высоте
Площадь трапеции равна произведению полусуммы ее оснований на высотугде S – площадь трапеции,
a, b – длины основ трапеции,
c, d – длины боковых сторон трапеции,p = a + b + c + d – полупериметр трапеции. 2
Формулы площади выпуклого четырехугольника

-
Формула площади четырехугольника по длине диагоналей и углу между ними
Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними:
где S – площадь четырехугольника,
d1, d2 – длины диагоналей четырехугольника,
α – угол между диагоналями четырехугольника. -
Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности)
Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности
S = p · r
-

Формула площади четырехугольника по длине сторон и значению противоположных углов
S = √(p – a)(p – b)(p – c)(p – d) – abcd cos2θ
где S – площадь четырехугольника,
a, b, c, d – длины сторон четырехугольника,
p = a + b + c + d2 – полупериметр четырехугольника,
θ = α + β2 – полусумма двух противоположных углов четырехугольника.
-
Формула площади четырехугольника, вокруг которого можно описать окружность
S = √(p – a)(p – b)(p – c)(p – d)
Формулы площади круга

-
Формула площади круга через радиус
Площадь круга равна произведению квадрата радиуса на число пи.S = π r2
-
Формула площади круга через диаметр
Площадь круга равна четверти произведения квадрата диаметра на число пи.где S – Площадь круга,
r – длина радиуса круга,
d – длина диаметра круга.
Формулы площади эллипса
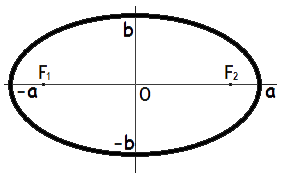
Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи.
S = π · a · b
где S – Площадь эллипса,
a – длина большей полуоси эллипса,
b – длина меньшей полуоси эллипса.
| Площадь | |
|---|---|
 , от фр. superficie , от фр. superficie |
|
| Размерность | L² |
| Единицы измерения | |
| СИ | м² |
| СГС | см² |
| Примечания | |
| скаляр |

Общая площадь всех трёх фигур составляет около 15-16 квадратиков
Пло́щадь — в узком смысле, площадь фигуры — численная характеристика, вводимая для определённого класса плоских геометрических фигур (исторически, для многоугольников, затем понятие было расширено на квадрируемые![]() фигуры) и обладающая свойствами площади
фигуры) и обладающая свойствами площади![]() [1]. Интуитивно, из этих свойств следует, что бо́льшая площадь фигуры соответствует её «большему размеру» (например, вырезанным из бумаги квадратом большей площади можно полностью закрыть меньший квадрат), a оценить площадь фигуры можно с помощью наложения на её рисунок сетки из линий, образующих одинаковые квадратики (единицы площади) и подсчитав число квадратиков и их долей, попавших внутрь фигуры[2] (на рисунке справа). В широком смысле понятие площади обобщается[1] на k-мерные поверхности в n-мерном пространстве (евклидовом или римановом), в частности, на двумерную поверхность в трёхмерном пространстве
[1]. Интуитивно, из этих свойств следует, что бо́льшая площадь фигуры соответствует её «большему размеру» (например, вырезанным из бумаги квадратом большей площади можно полностью закрыть меньший квадрат), a оценить площадь фигуры можно с помощью наложения на её рисунок сетки из линий, образующих одинаковые квадратики (единицы площади) и подсчитав число квадратиков и их долей, попавших внутрь фигуры[2] (на рисунке справа). В широком смысле понятие площади обобщается[1] на k-мерные поверхности в n-мерном пространстве (евклидовом или римановом), в частности, на двумерную поверхность в трёхмерном пространстве![]() .
.
Исторически вычисление площади называлось квадратурой. Конкретное значение площади для простых фигур однозначно вытекает из предъявляемых к этому понятию практически важных требований (см. ниже). Фигуры с одинаковой площадью называются равновеликими.
Общий метод вычисления площади геометрических фигур предоставило интегральное исчисление. Обобщением понятия площади стала теория меры множества, пригодная для более широкого класса геометрических объектов.
Для приближённого вычисления площади на практике используют палетку или специальный измерительный прибор — планиметр.
Определение понятия площади[править | править код]
Свойства[править | править код]

Множество измеримо по Жордану, если внутренняя мера Жордана равна внешней мере Жордана
Площадь — функция, которая обладает следующими свойствами[3][1]:
- Положительность, то есть площадь неотрицательная (скалярная) величина;
- Аддитивность, то есть площадь фигуры равна сумме площадей составляющих её фигур без общих внутренних точек;
- Инвариантность, то есть площади конгруэнтных фигур равны;
- Нормированность, то есть площадь единичного квадрата равна 1.
Из данного определения площади следует её монотонность, то есть площадь части фигуры меньше площади всей фигуры[3].
Квадрируемые фигуры[править | править код]
Первоначально определение площади было сформулировано для многоугольников, затем оно было расширено на квадрируемые фигуры. Квадрируемой называется такая фигура, которую можно вписать в многоугольник и в которую можно вписать многоугольник, причём площади обоих многоугольников отличаются на произвольно малую величину. Такие фигуры называются также измеримыми по Жордану[1]. Для фигур на плоскости, не состоящих из целого количества единичных квадратов, площадь определяется с помощью предельного перехода; при этом требуется, чтобы как фигура, так и её граница были кусочно-гладкими[4]. Существуют неквадрируемые плоские фигуры[1]. Предложенное выше аксиоматическое определение площади в случае плоских фигур обычно дополняют конструктивным, при котором с помощью палетки осуществляется собственно вычисление площади. При этом для более точных вычислений на последующих шагах используют палетки, у которых длина стороны квадрата в десять раз меньше длины у предыдущей палетки[5].
Площадь квадрируемой плоской фигуры существует и единственна. Понятие площади, распространённое на более общие множества, привело к определению множеств, измеримых по Лебегу, которыми занимается теория меры. В дальнейшем возникают более общие классы, для которых свойства площади не гарантируют её единственность[1].
Общий метод определения площади[править | править код]
Площадь плоской фигуры[править | править код]
На практике чаще всего требуется определить площадь ограниченной фигуры с кусочно-гладкой границей. Математический анализ предлагает универсальный метод решения подобных задач.
Декартовы координаты[править | править код]

Определённый интеграл как площадь фигуры
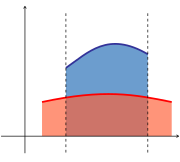
Площадь между графиками двух функций равна разности интегралов от этих функций в одинаковых пределах интегрирования
Площадь, заключённая между графиком непрерывной функции на интервале ![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
Площадь, заключённая между графиками двух непрерывных функций 
![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)

Полярные координаты[править | править код]
В полярных координатах: площадь, ограниченная графиком функции 

.
Площадь поверхности[править | править код]
Для определения площади кусочно гладкой поверхности в трёхмерном пространстве используют ортогональные проекции к касательным плоскостям в каждой точке, после чего выполняют предельный переход. В результате, площадь искривлённой поверхности A, заданной вектор-функцией 
То же в координатах:
Здесь 
Теория площадей[править | править код]
Теория площадей занимается изучением обобщений, связанных с распространением определения k-мерной площади с кусочно-гладкого погружения на более общие пространства. Для кусочно-гладкого погружения f площадь определяют способом, аналогичным указанному выше, при этом у площади сохраняются такие свойства как положительность, аддитивность, нормированность, а также ряд новых.
Единицы измерения площади[править | править код]

В одном квадратном сантиметре сто квадратных миллиметров
Метрические единицы[править | править код]
- Квадратный метр, производная единица Международной системы единиц (СИ); 1 м² = 1 са (сантиар);
- Квадратный километр, 1 км² = 1 000 000 м²;
- Гектар, 1 га = 10 000 м²;
- Ар (сотка), 1 а = 100 м²:
- Квадратный дециметр, 100 дм² = 1 м²;
- Квадратный сантиметр, 10 000 см² = 1 м²;
- Квадратный миллиметр, 1 000 000 мм² = 1 м²;
- Барн, 1 б = 10−28 м².
Русские устаревшие[править | править код]
- Квадратная верста = 1,13806 км²
- Десятина = 10925,4 м²
- Копна = 0,1 десятины — сенные покосы мерили копнами
- Квадратная сажень = 4,55224 м²
Мерами земли при налоговых расчётах были выть, соха, обжа, размеры которых зависели от качества земли и социального положения владельца. Существовали и различные местные меры земли: коробья, верёвка, жеребья и др.
Античные[править | править код]
- Актус
- Арура
- Центурия
- Югер
Другие[править | править код]
- Акр
- Рай = 1600 м² (40 м × 40 м).
- Квадратный парсек
- Планковская площадь (
) ≈ 2,612099 · 10−70 м2
Формулы вычисления площадей простейших фигур[править | править код]
Многоугольники[править | править код]
| Фигура | Формула | Переменные |
|---|---|---|
| Правильный треугольник | 
|
 — длина стороны треугольника — длина стороны треугольника
|
| Прямоугольный треугольник | 
|
 и и  — катеты треугольника — катеты треугольника
|
| Произвольный треугольник | 
|
 — сторона треугольника, — сторона треугольника,  — высота, проведённая к этой стороне — высота, проведённая к этой стороне
|

|
 и и  — любые две стороны, — любые две стороны,  — угол между ними — угол между ними
|
|
 (формула Герона) |
 , ,  и и  — стороны треугольника, — стороны треугольника,  — полупериметр — полупериметр 
|
|

|
 , ,  , ,  — координаты вершин треугольника (в случае обхода вершин по часовой стрелке получим положительный результат, иначе отрицательный) — координаты вершин треугольника (в случае обхода вершин по часовой стрелке получим положительный результат, иначе отрицательный)
|
|
| Квадрат | 
|
 — длина стороны квадрата — длина стороны квадрата
|
| Прямоугольник | 
|
 и и  — длины сторон прямоугольника (его длина и ширина) — длины сторон прямоугольника (его длина и ширина)
|
| Ромб | 
|
 и и  — длины диагоналей ромба — длины диагоналей ромба
|
| Параллелограмм | 
|
 и и  — длины стороны и опущенной на неё высоты соответственно — длины стороны и опущенной на неё высоты соответственно
|

|
 и и  — соседние стороны параллелограмма, — соседние стороны параллелограмма,  — угол между ними — угол между ними
|
|
| Трапеция | 
|
 и и  — основания трапеции, — основания трапеции,  — высота трапеции — высота трапеции
|
| Произвольный четырёхугольник |  (формула Брахмагупты) |
 , ,  , ,  , ,  — стороны четырёхугольника, — стороны четырёхугольника,  — его полупериметр, — его полупериметр,  — полусумма противолежащих углов четырёхугольника — полусумма противолежащих углов четырёхугольника
|
| Правильный шестиугольник | 
|
 — длина стороны шестиугольника — длина стороны шестиугольника
|
| Правильный восьмиугольник | 
|
 — длина стороны восьмиугольника — длина стороны восьмиугольника
|
| Правильный многоугольник | 
|
 — периметр, — периметр,  — количество сторон — количество сторон
|
| Произвольный многоугольник (выпуклый и невыпуклый) |  (метод трапеций) |
 — координаты вершин многоугольника в порядке их обхода, замыкая последнюю с первой: — координаты вершин многоугольника в порядке их обхода, замыкая последнюю с первой:  ; при наличии отверстий направление их обхода противоположно обходу внешней границы многоугольника ; при наличии отверстий направление их обхода противоположно обходу внешней границы многоугольника
|
| Произвольный многоугольник (выпуклый и невыпуклый) | Вычисление площадей многоугольников по способу Саррона[6]. Есть аналитическая формула. | Даны длины сторон многоугольника и азимутальные углы сторон |
Площади круга, его частей, описанных и вписанных в круг фигур[править | править код]
| Фигура | Формула | Переменные |
|---|---|---|
| Круг |  или или 
|
 — радиус, — радиус,  — диаметр круга — диаметр круга
|
| Сектор круга | 
|
 — радиус круга, — радиус круга,  — центральный угол сектора (в радианах) — центральный угол сектора (в радианах)
|
| Сегмент круга | 
|
 — радиус круга, — радиус круга,  — центральный угол сегмента (в радианах) — центральный угол сегмента (в радианах)
|
| Эллипс | 
|
 , ,  — большая и малая полуоси эллипса — большая и малая полуоси эллипса
|
| Треугольник, вписанный в окружность | 
|
 , ,  и и  — стороны треугольника, — стороны треугольника,  — радиус описанной окружности — радиус описанной окружности
|
| Четырёхугольник, вписанный в окружность |  (формула Брахмагупты) |
 , ,  , ,  , ,  — стороны четырёхугольника, — стороны четырёхугольника,  — его полупериметр — его полупериметр
|
| Многоугольник, описанный около окружности | 
|
 — радиус окружности, вписанной в многоугольник, — радиус окружности, вписанной в многоугольник,  — периметр многоугольника — периметр многоугольника
|
| Прямоугольная трапеция, описанная около окружности | 
|
 , ,  — основания трапеции — основания трапеции
|
Площади поверхностей тел в пространстве[править | править код]
| Тело | Формула | Переменные |
|---|---|---|
| Полная поверхность прямого кругового цилиндра | 
|
 и и  — радиус и высота соответственно — радиус и высота соответственно
|
| Боковая поверхность прямого кругового цилиндра | 
|
|
| Полная поверхность прямого кругового конуса | 
|
 и и  — радиус и образующая боковой поверхности соответственно — радиус и образующая боковой поверхности соответственно
|
| Боковая поверхность прямого кругового конуса | 
|
|
| Поверхность сферы (шара) |  или или 
|
 и и  — радиус и диаметр соответственно — радиус и диаметр соответственно
|
| Боковая поверхность прямой призмы | 
|
 — периметр основания, — периметр основания,  — высота — высота
|
| Полная поверхность произвольной призмы | 
|
 — площадь основания — площадь основания  — площадь боковой поверхности — площадь боковой поверхности
|
Исторический очерк[править | править код]
Площадь плоских фигур[править | править код]
Многие годы площадь считалась первичным понятием, не требующим определения. Основной задачей математиков являлось вычисление площади, при этом были известны основные свойства площади[3]. В Древнем Египте использовались точные правила вычисления площади прямоугольников, прямоугольных треугольников и трапеций, площадь произвольного четырёхугольника определялась приближённо как произведение полусумм пар противоположных сторон. Применение такой приближённой формулы связано с тем, что участки, площадь которых надо было померить, были в основном близки к прямоугольным и погрешность в таком случае оставалась небольшой. Историк математики А. П. Юшкевич предполагает, что египтяне могли и не знать, что пользуются приближённой формулой. В задаче 50 папируса Ринда содержится формула вычисления площади круга, которая считалась равной площади квадрата со стороной 8/9 диаметра круга[7]. Такими же формулами пользовались и в Вавилоне, однако для площади круга приближение было менее точным. Кроме того, вавилоняне могли приближённо посчитать площади правильных пяти-, шести- и семиугольника со стороной равной единице. В шестидесятиричной системе им соответствовали 1,40, 2,37,20 и 3,41, соответственно[8].
Основным приёмом вычисления площади при этом являлось построение квадрата, площадь которого равна площади заданной многоугольной фигуры, в частности в книге I «Начал» Евклида, которая посвящена планиметрии прямолинейных фигур, доказывается, что треугольник равновелик половине прямоугольника, имеющего с ним равные основания и высоту[9]. Метод разложения, основанный на том, что две равносоставленные фигуры равновелики, позволял также вычислить площади параллелограммов и любых многоугольников[5].
Следующим шагом было вычисление площадей круга, кругового сектора, лунок и других фигур. Основу вычислений при этом составлял метод исчерпывания многоугольниками[1][5], с которого берёт начало теория пределов. Метод заключается в построении последовательности площадей, которые при постепенном нарастании «исчерпывают» требуемую площадь. Метод исчерпывания, получивший своё название только в XVII веке, основан на аксиоме непрерывности Евдокса — Архимеда и приписывается Евдоксу Книдскому, который с его помощью показал, что площади кругов относятся друг к другу как квадраты их диаметров. Метод описан в «Началах» Евклида: аксиома Евдокса сформулирована в книге V, а сам метод исчерпывания и основанные на нём отношения — в книге XII[9]. Особого совершенства в применении метода достиг Архимед, который с его помощью посчитал площадь сегмента параболы и другие[10][11]. Труд Архимеда «О спиралях» включает много утверждений, касающихся площадей различных витков спирали и их отношений[12]. Архимеду принадлежит идея использования площадей или объёмов как вписанных, так и описанных фигур для определения требуемой площади или объёма[13].
Индийцы поначалу пользовались той же формулой для вычисления четырёхугольников, что египтяне и греки. Брахмагупта пользовался формулой для площади четырёхугольников, выраженной через его полупериметр., которая верна для вписанного в окружность четырёхугольника. Формулы вычисления площади обычно не доказывались, но демонстрировались с наглядными рисунками[14]. Формула Брахмагупты представляет собой аналог формулы Герона для площади треугольника, которую тот привёл в своей «Метрике»[15].
Развитие и обобщение метода исчерпывания произошло только в XVII веке. В 1604 году в работе «Три книги о центре тяжести тел» Валерио широко использует теорему, по которой разность между площадями вписанной и описанной фигур, составленных из параллелограммов можно сделать меньше любой данной площади[16]. Настоящий прорыв был сделан Кеплером, которому для астрономических расчётов нужно было уметь вычислять площадь эллипса. Кеплер рассматривал площадь как «сумму линий» и, разлиновывая эллипс с шагом в один градус, показал[17], что 
Площадь поверхности[править | править код]
Вычислением площадей кривых поверхностей занимался Архимед, определив, в частности, площадь поверхности шара[13]. В общем случае для определения площади поверхности нельзя пользоваться ни развёрткой (не подходит для сферы), ни приближением многогранными поверхностями, то есть аналогом метода исчерпывания. Последнее показал Шварц, построив для боковой последовательности цилиндра последовательности, которые приводят к разным результатам (так называемый сапог Шварца)[1][19].
Общий приём вычисления площади поверхности на рубеже XIX—XX веков предложил Минковский, который для каждой поверхности строил «окутывающий слой» малой постоянной толщины, тогда площадь поверхности будет приближённо равна объёму этого слоя, делённому на его толщину. Предельный переход при толщине, стремящейся к нулю даёт точное значение площади. Однако, для площади по Минковскому не всегда выполняется свойство аддитивности. Обобщение данного определения приводит к понятию линии по Минковскому и другим[20].
Примечания[править | править код]
- ↑ 1 2 3 4 5 6 7 8 9 10 Площадь // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 4.
- ↑ Чиркова, Наталья Ивановна, and Валентина Николаевна Зиновьева. Формирование у младших школьников представлений о площади предметов и её измерении Архивная копия от 28 апреля 2019 на Wayback Machine // Вестник Калужского университета 1 (2017): 92-97.
- ↑ 1 2 3 Геометрия, 1966, с. 7—13.
- ↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — Изд. 6-е. — М.: ФИЗМАТЛИТ, 1966. — Т. 2. — С. 186—224. — 800 с.
- ↑ 1 2 3 4 Болтянский В. О понятиях площади и объёма. Архивная копия от 5 мая 2017 на Wayback Machine Квант, № 5, 1977, c.2—9
- ↑ Хренов Л. С. Вычисление площадей многоугольников по способу Саррона// Матем. просвещение. 1936. Выпуск 6. С. 12-15
- ↑ История математики, т. I, 1970, с. 30—32.
- ↑ История математики, т. I, 1970, с. 47—53.
- ↑ 1 2 История математики, т. I, 1970, с. 111—114.
- ↑ Исчерпывания метод // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 2.
- ↑ История математики, т. I, 1970, с. 101—105.
- ↑ Boyer & Merzbach, 2010, p. 127—128.
- ↑ 1 2 История математики, т. I, 1970, с. 117—124.
- ↑ История математики, т. I, 1970, с. 197—198.
- ↑ Boyer & Merzbach, 2010, p. 172, 219.
- ↑ История математики, т. II, 1970, с. 131—135.
- ↑ История математики, т. II, 1970, с. 166—171.
- ↑ История математики, т. II, 1970, с. 174—181.
- ↑ В. Н. Дубровский, В поисках определения площади поверхности Архивная копия от 27 июня 2017 на Wayback Machine. Квант. 1978. № 5. С.31—34.
- ↑ В. Н. Дубровский, Площадь поверхности по Минковскому Архивная копия от 15 февраля 2017 на Wayback Machine. Квант. 1979. № 4. С.33—35.
Литература[править | править код]
- Энциклопедия элементарной математики. Книга пятая. Геометрия / под редакцией П. С. Александрова, А. И. Маркушевича и А. Я. Хинчина. — М.: Наука, 1966. — 624 с.
- Рашевский П. К. Риманова геометрия и тензорный анализ. Изд. 3-е, М.: Наука, 1967.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — М.: ФИЗМАТЛИТ, 1960. — Т. 2. — 680 с. — ISBN 5-9221-0155-2.
- История математики: в 3 т / под редакцией А. П. Юшкевича. — М.: Наука, 1970. — Т. I: С древнейших времён до начала Нового времени.
- История математики: в 3 т / под редакцией А. П. Юшкевича. — М.: Наука, 1970. — Т. II: Математика XVII столетия.
- Boyer C. B., Merzbach U. C. A History of Mathematics. — John Wiley & Sons, 2010. — 640 p. Архивная копия от 9 июля 2019 на Wayback Machine (англ.)
Площадь многоугольника — это величина той части плоскости, которую занимает многоугольник.
Некоторые свойства площади фигур
-
Если многоугольники равны, то они имеют равные площади.
-
Если многоугольник состоит из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.

Рис. (1). Нахождение площади многоугольника
Рассмотрим, как найти площадь у разных фигур.
Площадь квадрата
Площадь квадрата равна квадрату его стороны.
, где
a
— длина стороны квадрата.
Площадь прямоугольника
Площадь прямоугольника равна произведению его длины на ширину (смежные стороны).
, где
a
и
b
— длина и ширина.
Площадь параллелограмма равна произведению основания на высоту.

Рис. (2). Параллелограмм
,
a
(
AD
и
CD
) — основание,
h
(
BE
и
BF
) — высота.
Площадь ромба равна половине произведения его диагоналей.

Рис. (3). Ромб

Рис. (4). Треугольник
Площадь треугольника равна половине произведения основания на высоту.
, где
a
(
AD
) — основание,
h
(
BE
) — высота треугольника.
Площадь прямоугольного треугольника равна половине произведения его катетов.

Рис. (5). Трапеция
Площадь трапеции равна половине суммы оснований, умноженной на высоту.
, где
a
(
BC
) и
b
(
AD
) — основания,
h
(
BE
) — высота.
Площадь круга и кругового сектора

Рис. (6). Круг
— площадь кругового сектора.
Более подробно ознакомиться с примерами можно здесь.
Площади фигур. Основные формулы.
Площадь треугольника.
| Формула | Рисунок | Расшифровка формулы |
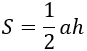 |
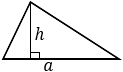 |
а – основание, h – высота, проведенная к этому основанию. Формула применима для любого треугольника. |
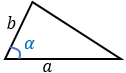 |
a, b – стороны, α – угол между этими сторонами. Формула применима для любого треугольника. |
|
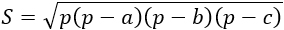 |
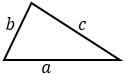 |
a, b, с – стороны, р – полупериметр (сумма трех сторон, деленная пополам). Формула применима для любого треугольника. |
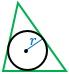 |
r – радиус вписанной в треугольник окружности, р – полупериметр (сумма трех сторон, деленная пополам). Формула применима для любого треугольника. |
|
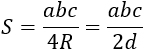 |
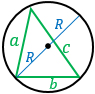 |
a, b, с – стороны, R – радиус описанной около треугольника окружности, d – диаметр описанной окружности. Формула применима для любого треугольника. |
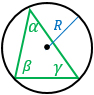 |
R – радиус описанной около треугольника окружности, α, β, γ – углы треугольника. Формула применима для любого треугольника. |
|
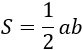 |
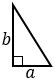 |
a, b – катеты. Формула применима для прямоугольного треугольника. |
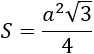 |
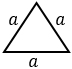 |
a – сторона. Формула применима для равностороннего (правильного) треугольника. |
Площадь квадрата и прямоугольника.
Площадь параллелограмма и ромба.
| Формула | Рисунок | Расшифровка формулы |
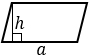 |
а – одна из сторон параллелограмма, h – высота, проведенная к этой стороне | |
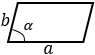 |
а, b – стороны параллелограмма, α – угол между этими сторонами | |
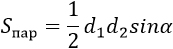 |
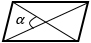 |
d1, d2 – диагонали, α – угол между диагоналями (можно брать любой угол, т.к. синусы смежных углов равны) |
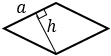 |
а – сторона ромба, h – высота, проведенная к этой стороне | |
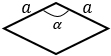 |
а – сторона ромба, α – угол между этими сторонами | |
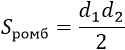 |
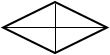 |
d1, d2 – диагонали ромба |
Площадь трапеции.
| Формула | Рисунок | Расшифровка формулы |
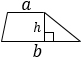 |
а, b – основания трапеции, h – высота. Формула применима для любой* трапеции. |
|
|
m – средняя линия трапеции, h – высота. Формула применима для любой трапеции. |
||
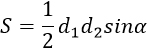 |
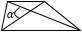 |
d1, d2 – диагонали трапеции, α – угол между диагоналями (можно брать любой угол, т.к. синусы смежных углов равны). Формула применима для любой трапеции. |
*Любая трапеция – это и равнобедренная, и прямоугольная, и тупоугольная, и произвольная 🙂
Площадь круга и кругового сектора.
Площадь многоугольника.
| Формула | Рисунок | Расшифровка формулы |
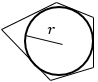 |
р – полупериметр (сумма всех сторон многоугольника, деланная на 2), r – радиус вписанной в этот многоугольник окружности. *Пятиугольник нарисован для примера. Формула работает как для правильного, так и для произвольного многоугольника, главное, чтобы в него можно было вписать окружность. |
Две фигуры называют равными, если одну их них можно так наложить на другую,
что эти фигуры совпадут.
Площади равных фигур равны. Их периметры тоже равны.
Площадь квадрата
Запомните!
![]()
Для вычисления площади квадрата нужно умножить его длину на саму себя.
S = a · a
Пример:

SEKFM = EK · EK
SEKFM = 3 · 3 = 9 см2
Формулу площади квадрата, зная
определение степени,
можно записать следующим образом:
S = a2
Площадь прямоугольника
Запомните!
![]()
Для вычисления площади прямоугольника нужно умножить его длину на ширину.
S = a · b
Пример:

SABCD = AB · BC
SABCD = 3 · 7 = 21 см2
Запомните!
![]()
Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.
Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.
Площадь сложных фигур
Запомните!
![]()
Площадь всей фигуры равна сумме площадей её частей.
Задача: найти площадь огородного участка.

Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя
правило выше.
Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.

SABCE = AB · BC
SEFKL = 10 · 3 = 30 м2
SCDEF = FC · CD
SCDEF = 7 · 5 = 35 м2
Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = SABCE + SEFKL
S = 30 + 35 = 65 м2
Ответ: S = 65 м2 — площадь огородного участка.
Свойство ниже может вам пригодиться при решении задач на площадь.
Запомните!
![]()
Диагональ прямоугольника делит прямоугольник на два равных треугольника.
Площадь любого из этих треугольников равна половине площади прямоугольника.
Рассмотрим прямоугольник:

АС — диагональ прямоугольника
ABCD. Найдём площадь треугольников

ABC и
 ACD
ACD
Вначале найдём площадь прямоугольника по формуле.
SABCD = AB · BC
SABCD = 5 · 4 = 20 см2
S
ABC = SABCD : 2
S
ABC = 20 : 2 = 10 см2
S
ABC =
S
ACD = 10 см2
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
3 декабря 2015 в 22:54
Ирина Петренко

Профиль
Благодарили: 0
Сообщений: 1

Ирина Петренко
Профиль
Благодарили: 0
Сообщений: 1
как написать правильно площадь треугольника?![]()
0
Спасибо
Ответить
9 декабря 2015 в 19:41
Ответ для Ирина Петренко
Тима Клюев

Профиль
Благодарили: 0
Сообщений: 8

Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
S(рисуешь мини треугольник) = ,,,,,
0
Спасибо
Ответить



