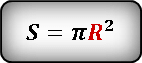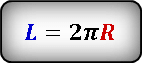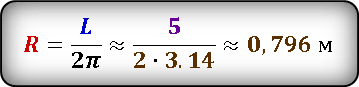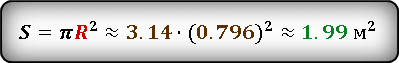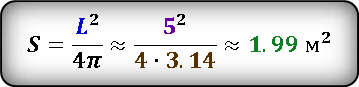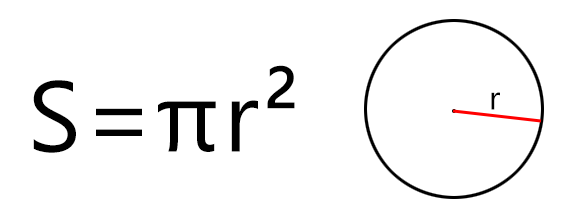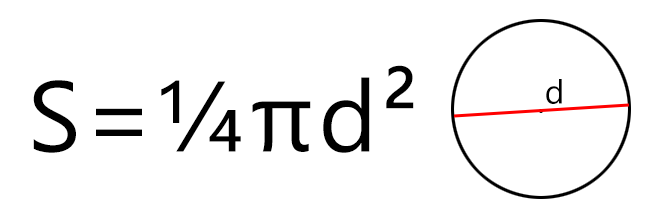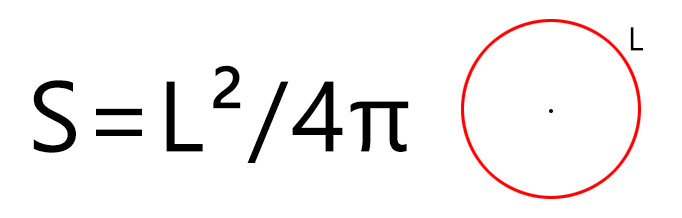Как найти площадь территории внутри окружности
Территория, находящаяся внутри кольцевой линии, называется Кировским городским районом. Найдите его площадь S (в км 2 ), если длина кольцевой ветки равна 50 км. В ответе укажите значение выражения S · π.
На рисунке изображена схема метро города N. Станция Театральная расположена между станциями Поперечная и Петровская. Если ехать по кольцевой линии (она имеет форму окружности), то можно последовательно попасть на станции Петровская, Маяковская, Владимирская, Международная, Сельская. Жёлтая ветка включает в себя станции Международная, Ломоносовская, Горная, Проспект славы.
Для станций, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Станции | Международная | Ломоносовская | Театральная | Проспект славы |
|---|---|---|---|---|
| Цифры |
Если ехать по кольцевой линии (она имеет форму окружности), то можно последовательно попасть на станции Петровская, Маяковская, Владимирская, Международная, Сельская, значит, Международная отмечена цифрой 2. Жёлтая ветка включает в себя станции Международная, Ломоносовская, Горная, Проспект славы, поэтому Ломоносовская отмечена цифрой 6, а Проспект славы цифрой 3. Станция Театральная расположена между станциями Поперечная и Петровская, следовательно, Театральная отмечена цифрой 4.
Бригада меняет рельсы на участке между станциями Поперечная и Театральная протяжённостью 13,8 км. Работы начались в понедельник. Каждый рабочий день бригада меняла по 300 метров рельсов. По субботам и воскресеньям замена рельсов не осуществлялась, но проезд был закрыт до конца всего ремонта. Сколько дней был закрыт проезд между указанными станциями?
Заметим, что станция Театральная отмечена на схеме цифрой 4. Поскольку бригада меняла по 300 метров рельсов в день, на замену рельс на всём участке ушло дней. Поскольку работы велись только с понедельника по пятницам, на замену рельс на данном участке ушло недель. Значит, проезд между указанными станциями был закрыт дня.
Аналоги к заданию № 366648: 367626 367634 367639 Все
Площадь круга: как найти, формулы
О чем эта статья:
площадь, 6 класс, 9 класс, ЕГЭ/ОГЭ
Определение основных понятий
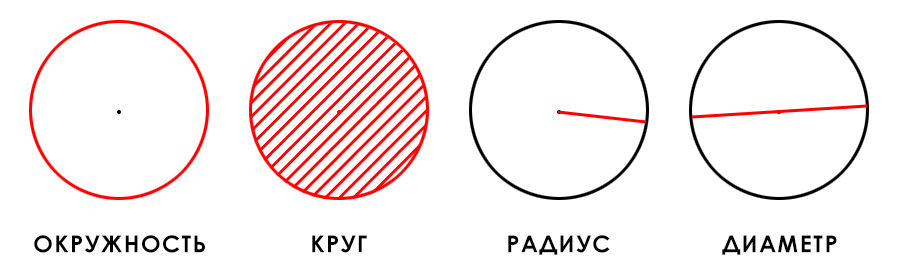
Прежде чем погрузиться в последовательность расчетов и узнать, чему равна площадь круга, важно выяснить разницу между понятиями окружности и круга.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии, не превышающем радиус.
Если говорить простым языком, окружность — это замкнутая линия, как, например, кольцо и шина. Круг — плоская фигура, ограниченная окружностью, как монетка или крышка люка.
Формула вычисления площади круга
Давайте разберем несколько формул расчета площади круга. Поехали!
Площадь круга через радиус
S = π × r 2 , где r — это радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она приблизительно равна 3,14.
Площадь круга через диаметр
S = d 2 : 4 × π, где d — это диаметр.
Площадь круга через длину окружности
S = L 2 : (4 × π), где L — это длина окружности.
Популярные единицы измерения площади:
- квадратный миллиметр (мм 2 );
- квадратный сантиметр (см 2 );
- квадратный дециметр (дм 2 );
- квадратный метр (м 2 );
- квадратный километр (км 2 );
- гектар (га).
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Задачи. Определить площадь круга
Мы разобрали три формулы для вычисления площади круга. А теперь тренироваться — поехали!
Задание 1. Как найти площадь круга по диаметру, если значение радиуса равно 6 см.
Диаметр окружности равен двум радиусам.
Используем формулу: S = π × d 2 : 4.
Подставим известные значения: S = 3,14 × 12 2 : 4.
Ответ: 113,04 см 2 .
Задание 2. Найти площадь круга, если известен диаметр, равный 90 мм.
Используем формулу: S = π × d 2 : 4.
Подставим известные значения: S = 3,14 × 90 2 : 4.
Ответ: 6358,5 мм 2 .
Задание 3. Найти длину окружности при радиусе 3 см.
Отношение длины окружности к диаметру является постоянным числом.
Получается: L = d × π.
Так как диаметр равен двум радиусам, то формула длины окружности примет вид: L = 2 × π × r.
Подставим значение радиуса: L = 2 × 3,14 × 3.
Ответ: 18,84 см 2 .
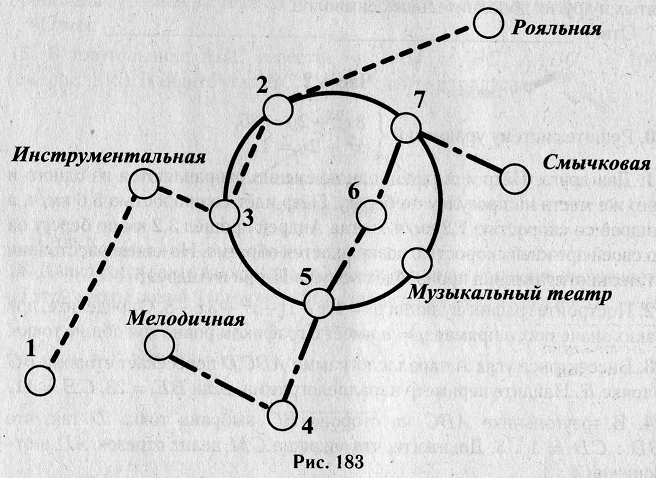
Решение №1338 На рисунке 183 изображена схема метро в городе К. Если ехать по веткам метро, то ближайшей к Рояльной …
На рисунке 183 изображена схема метро в городе К. Если ехать по веткам метро, то ближайшей к Рояльной является Клавишная станция, а ближайшая к Смычковой – Скрипичная. От четырёх станций можно уехать только в одну сторону – это станции Рояльная, Мелодичная, Гитарная и Смычковая. Инструментальная станция находится между Гитарной и Симфонической станциями. Кольцевая ветка имеет форму окружности, на ней расположены станции Симфоническая, Клавишная, Скрипичная, Музыкальный театр и Балетная. Между Скрипичной и Балетной находится станция Аккорд. Валерий живёт около станции Концертная.
Источник задания: ОГЭ 2021 Математика, Ф.Ф. Лысенко. 40 вариантов.
Задание 1
Для станций, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр.
Решение
…ближайшей к Рояльной является Клавишная станция … (2)
….ближайшая к Смычковой – Скрипичная. (7)
От четырёх станций можно уехать только в одну сторону – это станции Рояльная, Мелодичная, Гитарная и Смычковая. (1)
Инструментальная станция находится между Гитарной и Симфонической станциями. (3)
Кольцевая ветка имеет форму окружности, на ней расположены станции Симфоническая, Клавишная, Скрипичная, Музыкальный театр и Балетная . (5)
Между Скрипичной и Балетной находится станция Аккорд. (6)
Ответ: 6532
Задание 2
Бригада меняет рельсы на участке между станциями Гитарная и Инструментальная. Работы начались в понедельник, и до конца всего ремонта проезд между этими станциями был закрыт. Каждый рабочий день бригада меняла по 350 метров, а по субботам и воскресеньям замена рельсов не производилась. Найдите расстояние между станциями Гитарная и Инструментальная, если проезд был закрыт в течение 18 дней. Ответ дайте в метрах.
Решение
18 дней это 2 недели и 4 дня. В эти две недели входит 4 нерабочих дня. Всего бригада работала:
18 – 4 = 14 дней
Отремонтированное расстояние между станциями:
14·350 = 4900 метров
Ответ: 4900
Задание 3
Территория, находящаяся внутри кольцевой линии, называется Большим городским районом, его площадь равна 16 км 2 . Найдите длину l кольцевой линии (в километрах). В ответе укажите .
Решение
Территория имеет площадь круга. Найдём радиус из формулы:
S● = πR 2 = 16 км 2
Длина окружности l находится по формуле:
Ответ укажем в виде :
Ответ: 8
Задание 4
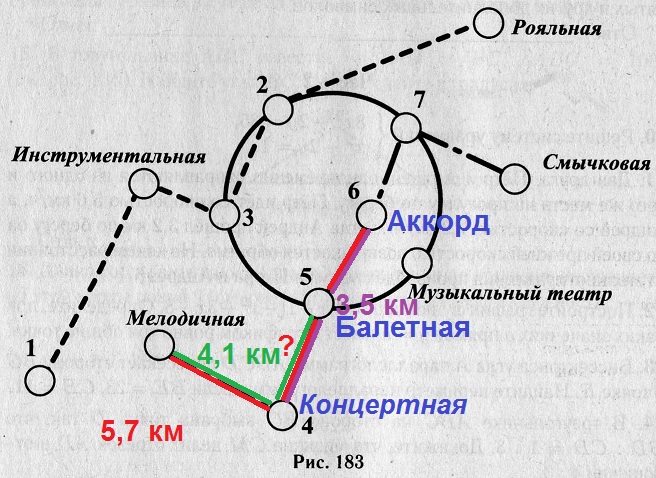
Найдите протяжённость пути по железной дороге (в километрах) между станциями Концертная и Балетная, если длина участка железной дороги между станциями Мелодичная и Аккорд равна 5,7 км, между станциями Мелодичная и Балетная – 4,1 км, а между станциями Концертная и Аккорд – 3,5 км.
Решение
Изобразим условие графически:
Если сложить расстояние фиолетового и зелёного участков, то участок Концертная – Балетная сложится дважды, и полученная сумма будет больше Аккорд – Мелодичная , ровно на длину нужного нам участка Концертная – Балетная.
Найдём расстояние Концертная – Балетная:
4,1 + 3,5 = 7,6 км
7,6 – 5,7 = 1,9 км
Ответ: 1,9
Задание 5
Школьник Валерий приехал в город D на летние каникулы. Он планирует совершить 65 поездок на метро. Для оплаты поездок можно покупать различные карточки. Стоимость одной поездки для разных видов карточек различна. После каникул Валерий уедет из города D, и неиспользованные карточки обнулятся. Во сколько рублей обойдётся самый дешёвый вариант?
Решение:
Стоимость одной поездки на «1» карточке равна (со скидкой заплатим 80%):
50·0,8 = 40 руб
На «15» карточке равна 46 руб.
На «25» карточке равна (со скидкой заплатим 90%):
42·0,9 = 37,8 руб
Самое выгодное 2 раза проехать по карточке «25» по 25 поездок и оставшиеся 15 по карточке «1». Это будет стоить:
2·25·37,8 + 15·40 = 1890 + 600 = 2490 руб
Это явно дешевле безлимита и всех остальных вариантов.
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/ploshad-kruga
[/spoiler]
|
Территория, находящаяся внутри кольцевой линии, называется Приморским городским районом. Найдите его площадь если длина кольцевой ветки равна 60 км. В ответе укажите значение выражения Длина кольцевой дороги – это, по сути нашего вычисления, есть длина окружности. Для вычисления площади круга, который ограничен данной окружностью, нам надо узнать радиус этого круга. Зная длину окружности сделать это будет несложно. Формулы длины окружности и площади круга имеют общую зависимость – число Пи и радиус окружности (круга) Заметим, что число Пи постоянно и равно 3,14 Вначале узнаем радиус из формулы С = 2π ; Получим R = 9,6 Затем найденное значение радиуса подставим в формулу площади круга S = πR². После вычислений получаем: 286,38 квадратных километров. (небольшая погрешность возможна при округлении значения радиуса) автор вопроса выбрал этот ответ лучшим Vanessa Mai более года назад S это площадь круга и она равна Пи•R^2, как все конечно хорошо помнят из курса школы 6-го класса. Нам известно, что длина окружности равна 60 км. Из формулы длины окружности L=2•Пи•R, можно рассчитать радиус R по преобразованной формуле R=L/2•Пи. Значит при значении Пи равном 3,1415926535 радиус круглого района равен: R=60/2•Пи= 9,5492965 км Тогда площадь круглого района по формуле Пи-Эр-Квадрат равна: S= Пи•R^2= Пи•9,5492965^2= 286,478892 кв. км (при значении Пи равном 3,1415926535). Но целью задачи является не найти площадь круглого Приморского городского района ограниченного кольцевой линией метро, а её произведение на число Пи=3,1415926535. S•Пи= 286,478892•3,1415926535 = 899,9999825 Что всего лишь на менее, чем две десятитысячных меньше 900. Отнесу это к неточности числа Пи в калькуляторе ОС Windows-7 и объявляю ответом: 900 кв. км. Конгламерантус 2 года назад Нам известна длина кольцевой окружности (ветки), это 60 километров. Для вычислений вам в помощь число π. Из курса школьной математики мы знаем, что величина числа π постоянна и равна 3,14. Для начала вычислим площадь этого круга. Формула площади круга S = πR². R это радиус, и равен он 9,6. Нам помогла формула С = 2πR. Теперь, когда мы знаем чему равен радиус, подставим это значение в формулу для вычисления площади заданного круга. При этом итоговая формула будет иметь следующий вид: S = π(C/ 2π)². Далее нам потребуется калькулятор для проведения математических вычислений. Полученный результат будет равен примерно 286,38. Единицы измерения квадратные километры. Урания 2 года назад Территорию, находящуюся внутри кольцевой ветки можно отнести к кругу. Напишем известную формулу для площади круга: S = πR²; Где R – это радиус окружности. Формула длины окружности круга (периметр окружности) вычисляется по формуле: С = 2πR; Где С – это и есть известная нам длина окружности (60 км). Число π – это постоянная величина, равная – 3,14. Из последней формулы находим радиус окружности: R = C/2π Подставляем это значение радиуса в первую формулу площади круга и получаем: S = π(C/ 2π)²; После возведения в квадрат и сокращения получаем окончательную формулу для площади круга, выраженную через его длину окружности: : S = C²/4π Подставляем известные числовые данные: S = 60²/4 π = 3600/4 π= 286,6 км. То есть площадь внутри кольцевой ветки будет равна – 286,6 км P. S. По окончательной формуле S = C²/4π можно рассчитать площадь любого круга, когда нам известна длина его окружности. Ира ЛДВО на БВ 2 года назад Вся хитрость данного вопроса сосредоточена не в числовых выражениях, а в символах нужно составить ответ так, чтобы в решении присутствовали знаки S*π Задача не так проста, как кажется. При произведении площади на число пи, получится ерунда. Но мы сначала разложим S на πи прочие производные, а потом подумаем. S = πR² π здесь на в квадрате, в квадрате R. Вот так задача. Пробуем её решить иезуитским методом. Если принять то, что S это не символ площади, по типу “Х” То Х = R² = S Теперь площадь окружности равна S*π. А числовые значения вычисляются просто: Sокр = 3.14 х (60 : 6.28)² = 286.478 = ~ 286 км² Simple Ein 2 года назад Кольцевая дорога – это круговая дорога. Значит нам необходимо найти площадь круга. Площадь круга рассчитывается по формуле S = ПR^2. П – константа, которая равна 3,14. R – радиус окружности. Он неизвестен. Найдем радиус окружности из формулы площади окружности. С = 2ПR. Выразим R. R=C/2П. Подставим значение радиуса в формулу площади круга. S=П(C/2П)^2. Сократим П. S=(C/2)^2/П. Ответ задачи просят записать в формате SП. SП= (C/2)^2. Подставляем числовые значение. SП=(60/2)^2=30^2=900 квадратных километров. Евгений трохов 3 года назад Кольцевая линия-это некая окружность. Длина окружности С=2*рi*r Площадь круга- S=pi*r^2,отсюда: S=pi*(C/2pi)^2=(C^2)/4pi=60*60/4*3,14=286,62 kv.km В задаче нужно найти S*pi. S*pi=(C^2)/4=60*60/4=900. Ответ-900 Ира ЛДВО на БВ более года назад Снова глянув на эту задачу вдруг до меня дошло, что ответ надо было указать просто числом в довольно странном формате: S*π? Более года назад, я решила эту задачу в ответе выше. И у меня вышло: S =286.478 = ~ 286 км². А теперь надо это умножить на пи. и получится: S*π = 286.478*π = 899.9971802150967874. А это длинное число фактически равно 900, ведь всего-то трёх тысячной не хватает. Теперь мой новый ответ, как дополнение к старому: S*π = 900 NotBroKen 2 года назад Поскольку длина кольцевой ветки 60 км, мы можем найти радиус за формулой на фото, R = C/2π, 60/2*3,14=9,5, 9.55 радиус Дальше за ранее известной нам формулой, которую можно посмотреть на фото, ищем ответ на наш вопрос, какая же площадь S = πR^2, 3,14*9,5*9,5=286,площадь Приморского городского района равна 286 километров квадратных. Ответ на ваш вопрос: площадь равна 286 километров квадратных Роза Зимняя 2 года назад Для того, чтобы найти площадь круга по длине окружности, сначала нужно по этой самой длине окружности вычислить радиус. Это можно сделать по формуле: Получаем 60/6,28=9,55 – радиус. Имея радиус можем воспользоваться формулой площади круга: Число пи – величина постоянная – умножается на квадрат радиуса. Получаем 286,38 – это и есть площадь данного района. ralinaa 2 года назад Мы знаем, что длина ветки равна 60 км. Для начала найдем радиус по формуле: R = C/2π, где число π всегда равен 3,14. Получаем 60/2*3,14=9,5 – это радиус. Далее находим площадь по формуле: S = πR2 S=3,14*9,5*9,5=286 км Ответ: площадь равна 286 км. Знаете ответ? |
Площадь сегмента круга
- Главная
- /
- Математика
- /
- Геометрия
- /
- Площадь сегмента круга
Чтобы посчитать площадь сегмента круга воспользуйтесь нашим онлайн калькулятором:
Онлайн калькулятор
По углу и радиусу
Угол α =
Радиус r =
Площадь сегмента круга
Sск =
0
Округление ответа: Округление числа π:
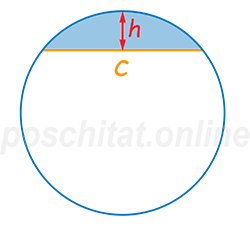
По длине хорды и высоте сегмента
Хорда c =
Высота сегмента h =
Площадь сегмента круга
Sск =
0
Округление ответа:
По высоте и радиусу (или диаметру)
=
Высота сегмента h =
Площадь сегмента круга
Sск =
0
Округление ответа:
Просто введите данные и получите ответ.
Теория
Площадь сегмента окружности через угол и радиус
Чему равна площадь сегмента окружности Sск, если её радиус r, а угол сегмента α ?
Формула
В градусах:
Sск = r²2 ⋅ (π ⋅ α180° – sin α)
В радианах:
Sск = r²2 ⋅ (α – sin α)
Пример
К примеру, посчитаем площадь сегмента круга, имеющего радиус r = 2 см, а угол сегмента ∠α = 45°:
Sск = 2²2 ⋅ (3.14 ⋅ 45180 – sin 45) = 2 ⋅ (0.785 – 0.707) = 0.156 см²
Площадь сегмента окружности через хорду и высоту сегмента
Чему равна площадь сегмента окружности Sск, если длина хорды c, а высота сегмента h ?
Чтобы посчитать площадь сегмента, нам для начала потребуется вычислить радиус окружности r и угол сегмента α. А затем воспользоваться формулой площади сегмента из предыдущего параграфа.
Формула
Радиус круга:
r = c² + 4h²8h
Угол сегмента:
∠α = 2 ⋅ arcsinc2r
Пример
К примеру, посчитаем площадь сегмента круга, имеющего высоту h = 2 см и длину хорды c = 5 см:
r = 5² + 4⋅2²8⋅2 = 25 + 1616 = 2.5625 см∠α = 2 ⋅ arcsin52 ⋅ 2.5625 = 2 ⋅ arcsin 0.9756 ≈ 2.7 radSск = 2.5625²2 ⋅ (2.7 – sin 2.7) = 3.2832 ⋅ (2.7 – 0,427) = 7.46 см²
Площадь сегмента окружности через высоту и радиус (или диаметр)
Чему равна площадь сегмента окружности Sск, если его высота h, а радиус r ?
Если нам известен не радиус, а диаметр, то делим его на 2 и получаем радиус (r = d ÷ 2).
Далее нам остаётся определить угол сегмента α. А затем воспользоваться формулой площади сегмента, описанной выше.
Формула
Угол сегмента:
∠α = 2 ⋅ arccosr – hr
Пример
К примеру, посчитаем площадь сегмента круга, имеющего высоту h = 1 см, а диаметр окружности d = 4 см:
r = 4 ÷ 2 = 2 см
∠α = 2 ⋅ arccos2 – 12 = 2 ⋅ arccos 0.5 = 2.094 radSск = 2²2 ⋅ (2.094 – sin 2.094) = 2 ⋅ (2.094 – 0.866) = 2.456 см²
См. также
Условие задачи:
Длина окружности 5 м. Найти площадь круга, ограниченного этой окружностью.
Дано:
Длина окружности, L = 5 м
Пояснение к рисунку:
O – центр окружности
Найти площадь круга: S
Решение
Используем формулу площади круга через радиус. Но нам пока не известен радиус, его надо найти.
Определить радиус, нам поможет формула длины окружности.
После преобразования, выразим радиус через длину окружности и подставим значения.
Результат получился приблизительным, потому что число π нельзя выразить точно, оно имеет бесконечное количество знаков после запятой. В данном случаи, мы взяли π ≈ 3.14
Получили значение радиуса окружности.
В формулу площади круга, подставляем найденное значение радиуса.
Ответ:
Если в формулу площади круга подставить выраженный радиус через длину окружности, то получим следующую формулу, в которой площадь круга сразу выражена через длину окружности. Проверим, подставив наше значение
Калькулятор для расчета площади круга
- Подробности
-
Опубликовано: 04 сентября 2017
-
Обновлено: 13 августа 2021
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
Формула (формулы) площади круга
Найти площадь круга можно разными способами, в зависимости от известных данных.
По радиусу
Если дан только радиус, то площадь составит произведение константы Пи на квадрат радиуса. Расчёт будет по формуле (где r – радиус, а π – константа, равная 3,1415…):
Например, если радиус равен 2 метра, то площадь круг можно вычислить так S = 3,14 × 22 = 3,14 × 4 = 12,56 м2 (квадратных метров).
Через диаметр
Если известен диаметр, то площадь круга будет равняться одной четвёртой произведения Пи и квадрата диаметра. Формула площади круга будет такой (где d – диаметр, а π – константа, равная 3,1415…):
К примеру, если диаметр круга (площадь поверхности пиццы) составляет 35 сантиметров, то площадь такого круга будет равна S = ¼ × 3,14 × 352 = ¼ × 3,14 × 1225 = 962 см2 (квадратных сантиметра).
Через длину окружности
Если мы знаем только длину окружности (периметр круга), то рассчитать площадь фигуры можно по формуле (где L – длина окружности, а π – константа, равная 3,1415…):
Например, если длинна окружности составляет 120 мм, тогда площадь круга будет равна S = 1202 / (4 × 3,14) = 14 400 / (4 × 3,14) = 1146,5 мм2 (квадратных миллиметров).
Какие термины используются для поиска площади круга?
Для вычисления площади круга, в формулах были использованы следующие термины, значение которых нужно знать, чтобы точно понимать принципы расчета.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии, не превышающем радиус.
Диаметр — отрезок, соединяющий две точки на окружности и проходящий через центр окружности. Диаметр равен двум радиусам.
Радиус — отрезок, который соединяет центр окружности и любую точку на ней.
Число π (пи) — математическая постоянная, равная отношению длины окружности к её диаметру. Пи равняется примерно 3,14.
Площадь круга и размеры пицц
Люди не всегда верно сопоставляют площадь круга и диаметры. К примеру, сможете ли вы ответить:
Что больше: 2 пиццы диаметром 25 см или 1 пицца диаметром 40 см?
Интуитивно кажется, что 2 пиццы, так как в сумме их радиусы дают 50 сантиметров, что больше, чем 40. Однако это неправильный вывод, так как сравнивать нужно не сумму диаметров, а сумму квадратов диаметров. То есть:
- 252 + 252 = 625 + 625 = 1250
- 402 = 1600
Так как ¼π является константой, то можно сравнивать только квадраты диаметров. Получается, что пицца 40 см больше, чем даже 2 пиццы размером 25 см. А вот если диаметр пиццы составляет 35 см, то 352 = 1225, и в этом случае 2 пиццы по 25 см будут иметь бОльшую площадь.
Площади усеченных частей круга
А также полезно знать следующие геометрические элементы, связанные с кругами и окружностями:
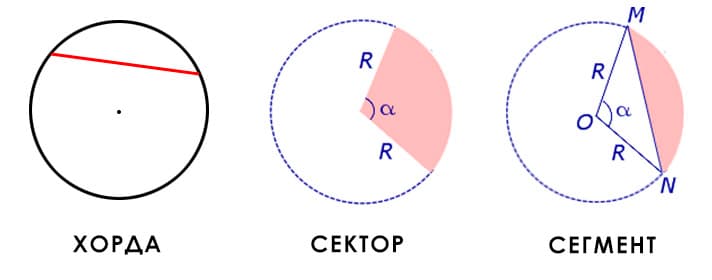
Хорда — отрезок, соединяющий любые две точки окружности.
Сектор — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Сектор является частью круга, а его площадь относится к площади круга так же, как и длина окружности сектора к длине всей окружности. Поэтому площадь сектора равна площади круга, умноженной на отношение длинны окружности сектора к длине окружности всего круга.
Но площадь сектора можно вычислить и по более простой формуле. Она равна длине дуги сектора, умноженной на половину радиуса:
S = sr/2
где S — площадь сектора, r — радиус круга.
Сегмент — это часть круга, ограниченная дугой и стягивающей её хордой.
Площадь сегмента можно найти по формулам:
S = r2sinα/ 2
где S — площадь сегмента, sinα — синус угла двух между радиусов до концов хорды, r — радиус круга.
Часто задаваемые вопросы о площади круга?
И конечно, стоит ответить на некоторые вопросы, которые возникают во время расчетов.
Входит ли окружность (периметр) в площадь круга?
Да, входит, ведь кругом являются все точки, удаленные от центра круга на расстояние, которое не превышает радиус.
Какие есть ещё калькуляторы для круга у вас на сайте?
У нас есть разнообразные калькуляторы, в частности калькуляторы: длины окружности, диаметра и площади круга. Для последней калькулятор находится на данной странице.
Хватит ли только диаметра, только радиуса или только длинны окружности для расчета площади круга?
Да, хватит чего-то одного, так как все 3 сущности можно вывести одну из другой, например, диаметр равен двум радиусам, а длина окружности – это диаметр, умноженный на число Пи.
Почему Пи равняется 3,1415926…, а не является «ровным» числом?
Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.
Кто впервые научился вычислять площадь круга?
Гиппократ Хиосский (не тот, в честь которого назвали клятву) первым сформулировал, что площадь круга пропорциональна квадрату его диаметра. Евдокс Книдский в IV веке до н. э. строго доказал это утверждение. А Архимед в III веке до н. э. нашёл число Пи и продемонстрировал, что оно чуть меньше, чем 3 и 1/7.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
- Калькулятор длины дуги. Рассчитайте онлайн длину дуги окружности по радиусу и углу или по формуле Гюйгенса.
- Калькулятор объема трубы. Рассчитайте онлайн объем трубы в куб. м. или литрах в зависимости от диаметра и длины трубопровода.
- Калькулятор объема пирамиды. Рассчитайте объем пирамиды по высоте, площади основания или стороне основания. Основание может быть любой формы.
- Калькулятор объема и площади усеченного конуса. Рассчитайте онлайн объем и площадь поверхности усеченного конуса по его радиусам и высоте.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии