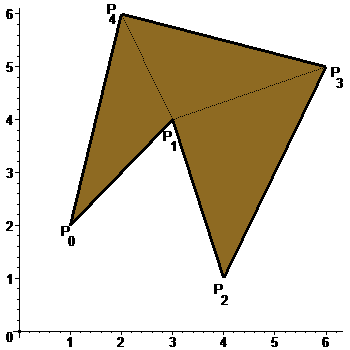Онлайн решение Пирамиды по координатам вершин
1) чертёж пирамиды по координатам её вершин;
2) длины и уравнения рёбер, медиан, апофем, высот;
3) площади и уравнения граней;
4) система линейных неравенств, определяющих пирамиду;
5) основания и точка пересечения медиан (центроид);
6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;
7) объём пирамиды;
8) основания, площади и уравнения биссекторов;
9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;
10) параметры и уравнения вписанной и описанной сфер;
Внимание! Этот сервис может не работать в браузере Internet Explorer.
Запишите координаты вершин пирамиды и нажмите кнопку.
Примечание: дробные числа записывайте
через точку, а не запятую.
Округлять до -го знака после запятой.
Как рассчитать объем пирамиды по координатам вершин? Методика и пример задачи
Часто в задачах школьного курса геометрии приходится решать задания, которые требуют использования комплексного подхода. Одной из таких задач является вычисление объема пирамиды по координатам вершин. Как решить эту геометрическую задачу — ответит приведенная ниже статья.
Что представляет собой пирамида?
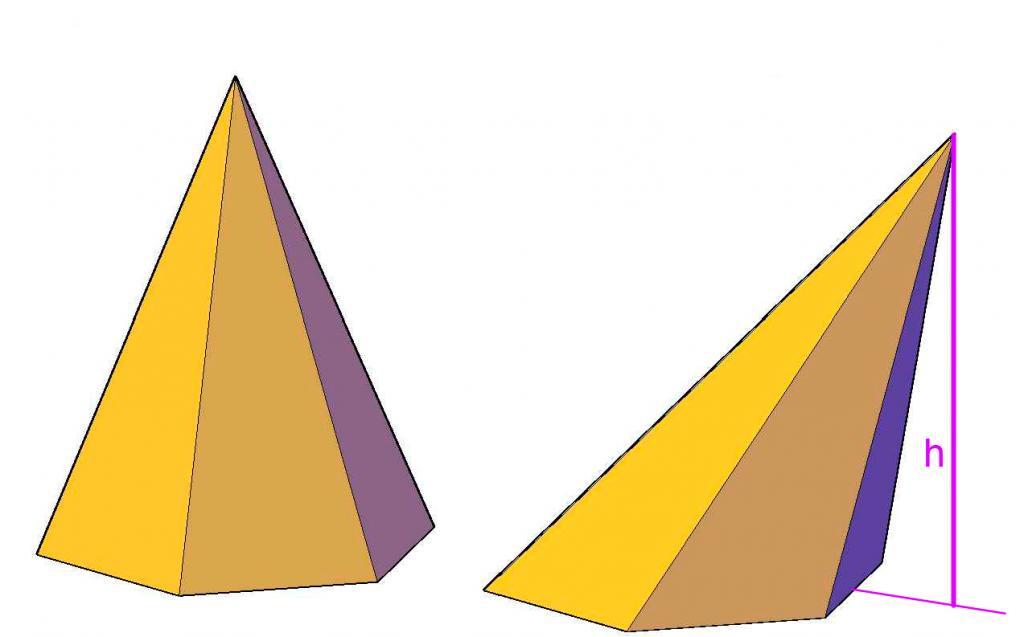
Говоря простыми словами, под этой фигурой понимают пространственный объект, ограниченный треугольными сторонами и одной многоугольной гранью, которая называется основанием. Многоугольное основание может быть произвольным n-угольником на плоскости, например, правильным треугольником, параллелограммом и так далее.
Любая пирамида имеет n + 1 грань, 2 * n ребер и n + 1 вершину. Вершины фигуры не являются равноправными. Так, существует единственная вершина, которая не принадлежит основанию. Она называется главной. Расстояние от нее до плоскости основания — это высота фигуры.
Пирамиды могут быть наклонными, если высота пересекает основание не в его центре, или прямыми, когда высота с основанием пересекается в геометрическом центре последнего. Также фигуры могут быть неправильными и правильными. Пирамиды правильные состоят из равноугольного и равностороннего основания и нескольких равнобедренных треугольников, которые друг другу равны.
Как рассчитывается объем пирамиды?
Прежде чем приводить методику вычисления по координатам вершин объема пирамиды, следует привести формулу, при помощи которой можно рассчитать эту величину для фигуры любого типа из рассматриваемого класса. Итак, объем пирамиды рассчитывается так:
Здесь So — это основания площадь, h — расстояние от главной вершины до основания, то есть высота пирамиды.
Таким образом, любая геометрическая задача на нахождение объема пирамиды сводится к расчету величин So и h.
Как найти объем пирамиды по координатам вершин: методика
Пирамида может быть представлена произвольным n-угольным основанием. Чтобы рассчитать его площадь, следует внимательно изучить условие задачи, в котором должно быть сказано, о каком типе n-угольника идет речь. Если это треугольник или параллелограмм, то расчет его площади по известным координатам очень прост: необходимо лишь найти векторное произведение соответствующих векторов сторон.
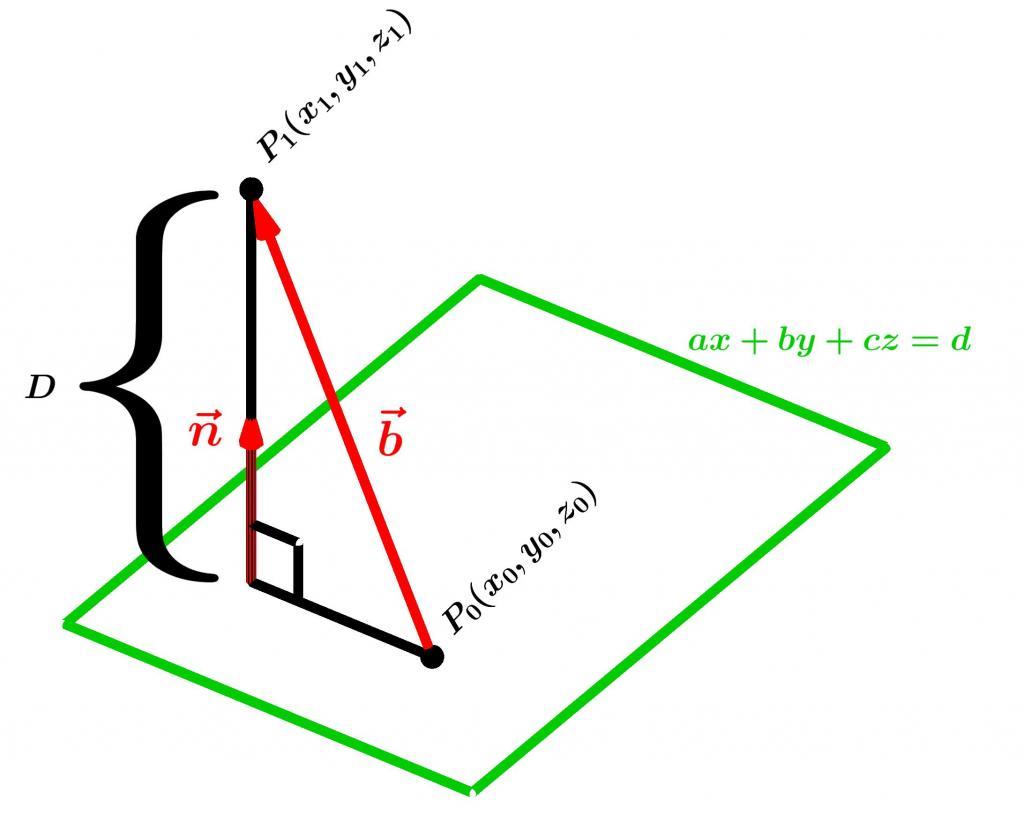
Вычислить высоту пирамиды также не представляет особого труда. Для этого следует из любых трех точек основания получить уравнение плоскости в общем виде, а затем нужно воспользоваться формулой расстояния между плоскостью и точкой (вершиной пирамиды). Формула имеет вид:
d = |(A * x1 + B * y1 + C * z1 + D)| / √(A2 + B2 + C2).
Здесь (x1; y1; z1) — координаты точки.
Уравнение плоскости имеет вид:
A * x + B * y + C * z + D = 0.
Задача с треугольной пирамидой
Решим задачу на примере самой простой пирамиды — треугольной. Условие простое: ниже даны координаты вершин пирамиды, объем найти нужно для фигуры, которая на этих координатах построена:
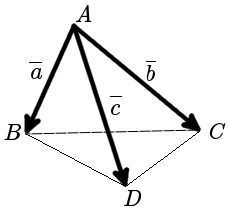
Положим, что основание пирамиды является треугольником ABC. Найдем длины векторов AB¯ и AC¯:
Векторное произведение AB¯ и AC¯ даст нам, с одной стороны, двойную площадь треугольника, то есть 2 * So, а с другой стороны, мы получим координаты нормального к плоскости вектора n¯, имеем:
n¯ = [AB¯ * AC¯] = (8; -10; -7).
Площадь треугольного основания равна полудлине вектора n¯, то есть:
So = √(82 + 102 + 72) / 2 = 7,3.
Прежде чем рассчитывать расстояние от D до плоскости ABC, необходимо записать уравнение плоскости. Три его коэффициента (A, B, C) мы уже знаем, они соответствуют координатам нормали n¯. Свободный член можно получить, подставив в уравнение координаты любой точки плоскости, например точки A, имеем:
D = -1 * (A * x1 + B * y1 + C * z1) = -1 * (8 * 1 + (-10) * 0 + (-7) * 3) = 13.
Тогда уравнение плоскости основания пирамиды принимает форму:
8 * x — 10 * y — 7 * z + 13 = 0.
Теперь применяем приведенную выше формулу для расчета расстояния от точки D(4; 3; 4) до найденной плоскости, получаем:
d = |(8 * 4 — 10 * 3 — 7 * 4 + 13)| / √(82 + 102 + 72) = 0,89.
Поскольку найденное значение расстояния d соответствует высоте пирамиды треугольной h, то можно воспользоваться формулой для объема фигуры:
V = 1 / 3 * So * h = 1 / 3 * 7,3 * 0,89 ≈ 2,166.
Полученное значение объема выражено в кубических единицах выбранной координатной системы.
[spoiler title=”источники:”]
http://ru.onlinemschool.com/math/assistance/vector/pyramid_volume/
http://b4.cooksy.ru/articles/vychislit-ploschad-piramidy-po-vektoram
[/spoiler]
| A ( ; ; ), B ( ; ; ), C ( ; ; ), D ( ; ; ) |
Примечание: дробные числа записывайте Округлять до -го знака после запятой. Онлайн калькулятор. Объем пирамиды (объем тетраэдра) построенной на векторах.Этот онлайн калькулятор позволит вам очень просто найти объем пирамиды или объем тетраэдра построенных на векторах. Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление объема пирамиды построенной на векторах и закрепить пройденый материал. Калькулятор для вычисления объема пирамиды (объема тетраэдра) построенной на векторахВыберите каким образом задается пирамида (тетраэдр): Введите значения векторов: Введите координаты вершин пирамиды: Инструкция использования калькулятора для вычисления объема пирамиды (объема тетраэдра) построенной на векторахВвод данных в калькулятор для вычисления объема пирамиды (объема тетраэдра) построенной на векторахВ онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел. Дополнительные возможности калькулятора вычисления объема пирамиды (объема тетраэдра) построенной на векторах
Теория. Объем пирамиды (объем тетраэдра) построенной на векторахОпределение Объем пирамиды (объем тетраэдра) построенной на векторах a , b и c равен шестой части модуля смешанного произведения векторов составляющих пирамиду: Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел. Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список! Добро пожаловать на OnlineMSchool. Вычислить площадь пирамиды по векторамОнлайн калькулятор. Объем пирамиды (объем тетраэдра) построенной на векторах.Этот онлайн калькулятор позволит вам очень просто найти объем пирамиды или объем тетраэдра построенных на векторах. Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление объема пирамиды построенной на векторах и закрепить пройденый материал. Калькулятор для вычисления объема пирамиды (объема тетраэдра) построенной на векторахВыберите каким образом задается пирамида (тетраэдр): Введите значения векторов: Введите координаты вершин пирамиды: Инструкция использования калькулятора для вычисления объема пирамиды (объема тетраэдра) построенной на векторахВвод данных в калькулятор для вычисления объема пирамиды (объема тетраэдра) построенной на векторахВ онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел. Дополнительные возможности калькулятора вычисления объема пирамиды (объема тетраэдра) построенной на векторах
Теория. Объем пирамиды (объем тетраэдра) построенной на векторахОпределение Объем пирамиды (объем тетраэдра) построенной на векторах a , b и c равен шестой части модуля смешанного произведения векторов составляющих пирамиду: Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел. Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список! Добро пожаловать на OnlineMSchool. Онлайн решение Пирамиды по координатам вершин1) чертёж пирамиды по координатам её вершин; 2) длины и уравнения рёбер, медиан, апофем, высот; 3) площади и уравнения граней; 4) система линейных неравенств, определяющих пирамиду; 5) основания и точка пересечения медиан (центроид); 6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням; 7) объём пирамиды; 8) основания, площади и уравнения биссекторов; 9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные; 10) параметры и уравнения вписанной и описанной сфер; Внимание! Этот сервис может не работать в браузере Internet Explorer. Запишите координаты вершин пирамиды и нажмите кнопку. |
| A ( ; ; ), B ( ; ; ), C ( ; ; ), D ( ; ; ) |
Аналитическая геометрия – задача на расчет пирамиды (тетраэдра)
Краткая теория
Вузовская аналитическая геометрия отличается от курса школьной геометрии. Главное отличие состоит в том, что она основным своим инструментом имеет набор алгебраических формул и методов вычислений. В основе аналитической геометрии лежит метод координат.
Аналитическая геометрия имеет набор формул, готовых уравнений и алгоритмов действия. Для успешного и правильного решения главное – разобраться и уделить задаче достаточно времени.
Данная задача является типовой в курсе аналитической геометрии и требует использования различных методов и знаний, таких как декартовые прямоугольные координаты и вектора в пространстве.
Пример решения задачи
Задача
Даны координаты
вершин пирамиды
. Найти:
Сделать чертеж.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Длина ребра
Длину ребра
найдем по
формуле расстояния между 2-мя точками:
Угол между ребрами
Угол между ребрами
и
найдем как угол
между направляющими векторами
и
:
Косинус угла между
векторами:
Угол между ребром и гранью. Векторное произведение
Вычислим угол между
ребром
и гранью
.
Для этого вычислим
координаты нормального вектора плоскости
–им будет
векторное произведение векторов
и
.
Найдем векторное произведение. Для этого
вычислим определитель:
Нормальный вектор
плоскости:
Синус угла:
Площадь грани
Вычислим площадь
грани
. Она будет численно равна половине модуля векторного
произведения векторов
и
:
Искомая площадь:
Объем пирамиды. Смешанное произведение векторов
Вычислим объем
пирамиды. Он будет равен шестой части модуля смешанного произведения векторов
и
:
Для того чтобы вычислить смешанное произведение, необходимо
найти определитель квадратной матрицы, составленной из координат векторов:
Искомый объем
пирамиды:
Уравнение прямой в пространстве
Вычислим уравнение
прямой
. Направляющим
вектором искомой прямой является вектор
. Кроме того, прямая проходит через точку
Уравнение искомой
прямой:
Уравнение плоскости
Вычислим уравнение
плоскости
. Нормальный вектор плоскости
. кроме того, плоскость проходит через точку
-уравнение
грани
Уравнение высоты, опущенной на грань
Составим уравнение
высоты, опущенной на грань
из вершины
:
Нормальный вектор
является
направляющим вектором высоты, кроме того, высота проходит через точку
Искомое уравнение
высоты:
Сделаем схематический чертеж:
Содержание
§
Вспомогательная страница к разделу
☞
ОПРЕДЕЛИТЕЛЬ
Геометрические приложения определителя
Уравнения кривых и поверхностей
Уравнение прямой, проходящей через точки плоскости с координатами $ (x_{1},y_1) $ и $ (x_{2},y_2) $:
$$
left|
begin{array}{lll}
x & y & 1 \
x_1 & y_1 & 1 \
x_2 & y_2 & 1
end{array}
right|=0 qquad iff qquad
left|
begin{array}{ll}
x-x_1 & y-y_1 \
x_2-x_1 & y_2-y_1
end{array}
right|=0 .
$$
Уравнение окружности, проходящей через точки плоскости с координатами $ (x_{1},y_1) , (x_2,y_2) $ и $ (x_{3},y_3) $ (окружности, описанной вокруг треугольника):
$$
left|
begin{array}{llll}
x^2+y^2 & x & y & 1 \
x_1^2+y_1^2 & x_1 & y_1 & 1 \
x_2^2+y_2^2 & x_2 & y_2& 1 \
x_3^2+y_3^2 & x_3 & y_3& 1
end{array}
right|=0 .
$$
При условии, что все три точки коллинеарны (лежат на одной прямой; см.
☞
ЗДЕСЬ ):
$$
left|
begin{array}{lll}
x_1 & y_1 & 1 \
x_2 & y_2 & 1 \
x_3 & y_3 & 1
end{array}
right|=0
$$
окружность вырождается в прямую
$$
left|
begin{array}{clll}
0 & x & y & 1 \
x_1^2+y_1^2 & x_1 & y_1 & 1 \
x_2^2+y_2^2 & x_2 & y_2& 1 \
x_3^2+y_3^2 & x_3 & y_3& 1
end{array}
right|=0 .
$$
Координаты центра окружности, проходящей через точки $ (x_{1},y_1) , (x_2,y_2) $ и $ (x_{3},y_3) $:
$$
x_C=frac{left|
begin{array}{lll}
x_1^2+y_1^2 & y_1 & 1 \
x_2^2+y_2^2 & y_2& 1 \
x_3^2+y_3^2 & y_3& 1
end{array}
right|}
{2left|
begin{array}{lll}
x_1 & y_1 & 1 \
x_2 & y_2 & 1 \
x_3 & y_3 & 1
end{array}
right|},quad
y_C=-frac{left|
begin{array}{lll}
x_1^2+y_1^2 & x_1 & 1 \
x_2^2+y_2^2 & x_2& 1 \
x_3^2+y_3^2 & x_3& 1
end{array}
right|}
{2left|
begin{array}{lll}
x_1 & y_1 & 1 \
x_2 & y_2 & 1 \
x_3 & y_3 & 1
end{array}
right|} .
$$
Т
Теорема [Птолемей]. Точки
$$ P_1=(x_{1},y_1) , P_2=(x_2,y_2), P_3 =(x_{3},y_3), P_4=(x_{4},y_4) $$
лежат на одной окружности или на одной прямой тогда и только тогда, когда выполнено равенство
$$
left|
begin{array}{cccc}
0 & |P_1P_2|^2 & |P_1P_3|^2 & |P_1P_4|^2 \
|P_1P_2|^2 & 0 & |P_2P_3|^2 & |P_2P_4|^2 \
|P_1P_3|^2 & |P_2P_3|^2 & 0 & |P_3P_4|^2 \
|P_1P_4|^2 & |P_2P_4|^2 & |P_3P_4|^2 & 0
end{array}
right|=0 .
$$
Здесь $ |P_jP_k|^2=(x_j-x_k)^2+(y_j-y_k)^2 $.
Доказательство, альтернативная геометрическая формулировка, а также пространственный аналог теоремы
☞
ЗДЕСЬ.
Уравнение плоскости, проходящей через точки пространства с координатами $ (x_{1},y_1,z_1) $, $ (x_{2},y_2,z_2) $ и $ (x_{3},y_3,z_3) $:
$$
left|
begin{array}{llll}
x & y & z & 1 \
x_1 & y_1 & z_1 & 1 \
x_2 & y_2 & z_2 & 1 \
x_3 & y_3 & z_3 & 1
end{array}
right|=0 .
$$
Уравнение сферы, проходящей через точки $ (x_{1},y_1,z_1) $, $ (x_{2},y_2,z_2) $, $ (x_{3},y_3,z_3) $ и $ (x_{4},y_4,z_4) $:
$$
left|
begin{array}{cllll}
x^2+y^2+z^2 & x & y & z & 1 \
x_1^2+y_1^2+z_1^2 & x_1 & y_1 & z_1 & 1 \
x_2^2+y_2^2+z_2^2 & x_2 & y_2 & z_2 & 1 \
x_3^2+y_3^2+z_3^2 & x_3 & y_3 & z_3 & 1 \
x_4^2+y_4^2+z_4^2 & x_4 & y_4 & z_4 & 1
end{array}
right|=0 .
$$
При условии, что все четыре точки компланарны (лежат в одной плоскости; см.
☞
ЗДЕСЬ ):
$$
left|
begin{array}{llll}
x_1 & y_1 & z_1 & 1 \
x_2 & y_2 & z_2 & 1 \
x_3 & y_3 & z_3 & 1 \
x_4 & y_4 & z_4 & 1
end{array}
right|=0
$$
сфера вырождается в плоскость. Координаты центра сферы:
$$
x_C=frac{left|
begin{array}{clll}
x_1^2+y_1^2+z_1^2 & y_1 & z_1 & 1 \
x_2^2+y_2^2+z_2^2 & y_2 & z_2 & 1 \
x_3^2+y_3^2+z_3^2 & y_3 & z_3 & 1 \
x_4^2+y_4^2+z_4^2 & y_4 & z_4 & 1
end{array}
right|}{2,left|
begin{array}{llll}
x_1 & y_1 & z_1 & 1 \
x_2 & y_2 & z_2 & 1 \
x_3 & y_3 & z_3 & 1 \
x_4 & y_4 & z_4 & 1
end{array}
right|},
y_C=-frac{left|
begin{array}{clll}
x_1^2+y_1^2+z_1^2 & x_1 & z_1 & 1 \
x_2^2+y_2^2+z_2^2 & x_2 & z_2 & 1 \
x_3^2+y_3^2+z_3^2 & x_3 & z_3 & 1 \
x_4^2+y_4^2+z_4^2 & x_4 & z_4 & 1
end{array}
right|}{2,left|
begin{array}{llll}
x_1 & y_1 & z_1 & 1 \
x_2 & y_2 & z_2 & 1 \
x_3 & y_3 & z_3 & 1 \
x_4 & y_4 & z_4 & 1
end{array}
right|},
z_C=frac{left|
begin{array}{clll}
x_1^2+y_1^2+z_1^2 & x_1 & y_1 & 1 \
x_2^2+y_2^2+z_2^2 & x_2 & y_2 & 1 \
x_3^2+y_3^2+z_3^2 & x_3 & y_3 & 1 \
x_4^2+y_4^2+z_4^2 & x_4 & y_4 & 1
end{array}
right|}{2,left|
begin{array}{llll}
x_1 & y_1 & z_1 & 1 \
x_2 & y_2 & z_2 & 1 \
x_3 & y_3 & z_3 & 1 \
x_4 & y_4 & z_4 & 1
end{array}
right|}
$$
§
Сформулированные выше геометрические задачи являются частными случаями общей задачи об
☞
ИНТЕРПОЛЯЦИИ.
Площади
Площадь треугольника с вершинами $ P_1=(x_{1},y_1) , P_2=(x_{2},y_2) $ и $ P_3=(x_{3},y_3) $ равна абсолютной величине (модулю) выражения
$$
frac{1}{2}
left|
begin{array}{lll}
1 & x_1 & y_1 \
1 & x_2 & y_2 \
1 & x_3 & y_3
end{array}
right| .
$$
Доказательство
☞
ЗДЕСЬ.
Квадрат площади треугольника $ P_{1}P_2P_3 $ выражается через квадраты длин его сторон по формуле
$$
S^2=-frac{1}{16}
left|
begin{array}{cccc}
0 & |P_1P_2|^2 & |P_1P_3|^2 & 1 \
|P_1P_2|^2 & 0 & |P_2P_3|^2 & 1 \
|P_1P_3|^2 & |P_2P_3|^2 & 0 & 1 \
1 & 1 & 1 & 0
end{array}
right| ,
$$
которая в развернутом виде
$$
=frac{1}{16}left(|P_1P_2|+|P_1P_3|+|P_2P_3| right)left(|P_1P_2|+|P_1P_3|-|P_2P_3| right)left(|P_1P_2|-|P_1P_3|+|P_2P_3| right)
left(-|P_1P_2|+|P_1P_3|+|P_2P_3| right)
$$
представляет собой формулу Герона.
Площадь треугольника с вершинами $ P_1=(x_{1},y_1,z_1) , P_2=(x_{2},y_2,z_2) $ и $ P_3=(x_{3},y_3,z_3) $ в $ mathbb R^{3} $ равна
$$
frac{1}{2} sqrt{ left|
begin{array}{lll}
1 & x_1 & y_1 \
1 & x_2 & y_2 \
1 & x_3 & y_3
end{array}
right|^2
+
left|
begin{array}{lll}
1 & x_1 & z_1 \
1 & x_2 & z_2 \
1 & x_3 & z_3
end{array}
right|^2+
left|
begin{array}{lll}
1 & y_1 & z_1 \
1 & y_2 & z_2 \
1 & y_3 & z_3
end{array}
right|^2
} .
$$
Выражение под радикалом можно преобразовать к виду
$$
detleft[left(
begin{array}{lll}
x_2-x_1 & y_2-y_1 &z_2- z_1 \
x_3-x_1 & y_3-y_1 & z_3- z_1
end{array}
right)cdot left(
begin{array}{ll}
x_2-x_1 & x_3-x_1 \
y_2-y_1 & y_3-y_1 \
z_2-z_1 & z_3-z_1
end{array}
right)right]
$$
с помощью теоремы Бине-Коши. Таким образом, площадь треугольника также равна
$$
frac{1}{2} sqrt{ left|
begin{array}{cc}
langle P_2P_1,P_2P_1 rangle & langle P_2P_1,P_3P_1 rangle \
langle P_2P_1,P_3P_1 rangle & langle P_3P_1,P_3P_1 rangle
end{array}
right|} ,
$$
где скобками $ langle , rangle $ обозначено скалярное произведение.
Площадь четырехугольника с вершинами $ P_1=(x_{1},y_1) , P_2=(x_{2},y_2), P_3=(x_{3},y_3), P_4=(x_4,y_4) $ равна абсолютной величине (модулю) выражения
$$
frac{1}{2}
left| begin{array}{cc}
x_1-x_3 & y_1-y_3 \
x_2-x_4 & y_2-y_4
end{array}
right| =frac{1}{2} left[(x_1-x_3)(y_2-y_4)-(x_2-x_4)(y_1-y_3)right]
$$
при условии, что стороны не пересекаются.
Площадь $ n_{} $-угольника $ P_{0}P_1dots P_{n-1} P_0 $ с вершинами $ P_0 = (x_{0},y_0) ,dots,
P_{n-1} = (x_{n-1},y_{n-1}) $ равна
абсолютной величине (модулю) выражения
$$
frac{1}{2} sum_{k=1}^{n-2}
left|
begin{array}{lll}
1 & x_0 & y_0 \
1 & x_k & y_k \
1 & x_{k+1} & y_{k+1}
end{array}
right|
$$
при условии, что стороны не пересекаются.
П
Пример. Найти площадь пятиугольника, изображенного на рисунке.
Решение. Имеем: $ P_{0} =(1,2),P_1= (3,4),P_2=(4,1), P_3=(6,5) , P_4=(2,6) $.
$$
S=frac{1}{2}Bigg(
left| begin{array}{ccc}
1& 1 & 2 \
1& 3 & 4 \
1& 4 & 1
end{array}
right| +
left| begin{array}{ccc}
1& 1 & 2 \
1& 4 & 1 \
1& 6 & 5
end{array}
right|
+
left| begin{array}{ccc}
1& 1 & 2 \
1& 6 & 5 \
1 & 2 & 6
end{array}
right|
Bigg) =
$$
$$
=frac{1}{2}(-8+14+17)=frac{23}{2} .
$$
Геометрический смысл суммирования будет более понятен, если перенумеровать точки, сделав стартовой $ P_{1} $: слагаемые в сумме
$$
frac{1}{2}Bigg(
left| begin{array}{ccc}
1& 3 & 4 \
1& 4 & 1 \
1& 6 & 5
end{array}
right| + left| begin{array}{ccc}
1& 3 & 4 \
1& 6 & 5 \
1& 2 & 6
end{array}
right| +
left| begin{array}{ccc}
1& 3 & 4 \
1& 2 & 6 \
1 & 1 & 2
end{array}
right| Bigg) = frac{1}{2}(10+7+6)
$$
теперь отвечают за площади треугольников, на которые разбит пятиугольник точечными линиями.
♦
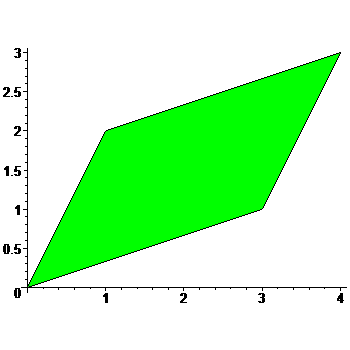
Площадь параллелограмма в $ {mathbb R}^{2} $ с вершинами $ (0,0), (x_{1},y_1) , (x_2,y_2), (x_1+x_2,y_1+y_2) $ равна абсолютной величине (модулю) определителя
$$
left|
begin{array}{ll}
x_1 & y_1 \
x_2 & y_2 \
end{array}
right| .
$$
П
Пример. Для $ x_{1} =3,y_1=1,x_2=1,y_2=2 $
имеем: $ S_{}=3cdot 2 – 1 cdot 1 = 5 $.
Площадь параллелограмма в $ {mathbb R}^{3} $ с вершинами $ (0,0,0), (x_{1},y_1,z_1) , (x_2,y_2,z_2), (x_1+x_2,y_1+y_2,z_1+z_2) $ равна
$$
sqrt{detleft[left(
begin{array}{lll}
x_1 & y_1 & z_1 \
x_2 & y_2 & z_2 \
end{array}
right)cdot left(
begin{array}{ll}
x_1 & x_2 \
y_1 & y_2 \
z_1 & z_2
end{array}
right)right]
}=sqrt{left|
begin{array}{cc}
x_1^2+y_1^2 + z_1^2 & x_1x_2+y_1y_2+z_1z_2 \
x_1x_2+y_1y_2+z_1z_2 & x_2^2+y_2^2 + z_2^2 \
end{array}
right|
} .
$$
Если применить к определителю произведения матриц теорему Бине-Коши, то получим следующее равенство
$$
detleft[left(
begin{array}{lll}
x_1 & y_1 & z_1 \
x_2 & y_2 & z_2 \
end{array}
right)cdot left(
begin{array}{ll}
x_1 & x_2 \
y_1 & y_2 \
z_1 & z_2
end{array}
right)right]=
left|
begin{array}{ll}
x_1 & y_1 \
x_2 & y_2 \
end{array}
right|^2+left|
begin{array}{ll}
x_1 & z_1 \
x_2 & z_2 \
end{array}
right|^2
+
left|
begin{array}{ll}
y_1 & z_1 \
y_2 & z_2 \
end{array}
right|^2 ,
$$
которое интерпретируется следующим образом: квадрат площади параллелограмма в $ mathbb R^{3} $ равен сумме квадратов площадей его проекций на координатные плоскости. Можно считать этот результат обобщением теоремы Пифагора.
Объемы
тетраэдра
Объем тетраэдра в $ mathbb R^{3} $ с вершинами $ P_1= (x_{1},y_1,z_1) ,P_2=(x_2,y_2,z_2) , P_3=(x_3,y_3,z_3) , P_4=(x_4,y_4,z_4) $ равен абсолютной величине (модулю) выражения
$$
frac{1}{6}
left|
begin{array}{llll}
1 & x_1 & y_1 & z_1 \
1 & x_2 & y_2 & z_2 \
1 & x_3 & y_3 & z_3 \
1 & x_4 & y_4 & z_4
end{array}
right| .
$$
Формула Тартальи (Кэли-Менгера) для квадрата объема тетраэдра через длины его ребер:
$$
V^2=frac{1}{288}
left|
begin{array}{ccccc}
0 & |P_1P_2|^2 & |P_1P_3|^2 & |P_1P_4|^2 & 1 \
|P_1P_2|^2 & 0 & |P_2P_3|^2 & |P_2P_4|^2 & 1 \
|P_1P_3|^2 & |P_2P_3|^2 & 0 & |P_3P_4|^2 & 1 \
|P_1P_4|^2 & |P_2P_4|^2 & |P_3P_4|^2 & 0 & 1 \
1 & 1 & 1 & 1 & 0
end{array}
right| .
$$
Доказательство
☞
ЗДЕСЬ.
Интересно было бы посмотреть, как эта формула выглядела в оригинале у Тартальи, если аппарат определителей был придуман лет на 250 позже…
=>
Если точки $ P_1,P_2,P_3,P_4 $ компланарны, т.е. тетраэдр вырождается в плоский четырехугольник, то формула Тартальи дает связь между сторонами четырехугольника и его диагоналями:
$$
left|
begin{array}{ccccc}
0 & |P_1P_2|^2 & |P_1P_3|^2 & |P_1P_4|^2 & 1 \
|P_1P_2|^2 & 0 & |P_2P_3|^2 & |P_2P_4|^2 & 1 \
|P_1P_3|^2 & |P_2P_3|^2 & 0 & |P_3P_4|^2 & 1 \
|P_1P_4|^2 & |P_2P_4|^2 & |P_3P_4|^2 & 0 & 1 \
1 & 1 & 1 & 1 & 0
end{array}
right|=0 , .
$$
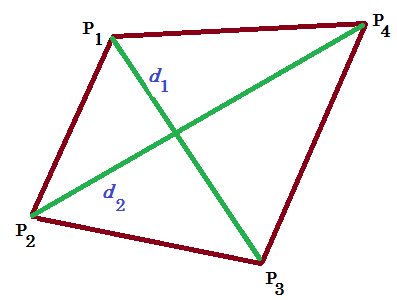
Применение тождества Сильвестра дает (в обозначениях рисунка):
$$
left|
begin{array}{cccc}
0 & |P_2P_3|^2 & d_2^2 & 1 \
|P_2P_3|^2 & 0 & |P_3P_4|^2 & 1 \
d_2^2 & |P_3P_4|^2 & 0 & 1 \
1 & 1 & 1 & 0
end{array}
right| cdot
left|
begin{array}{cccc}
0 & |P_1P_2|^2 & |P_1P_4|^2 & 1 \
|P_1P_2|^2 & 0 & d_2^2 & 1 \
|P_1P_4|^2 & d_2^2 & 0 & 1 \
1 & 1 & 1 & 0
end{array}
right|
=
$$
$$
=
left|
begin{array}{cccc}
|P_1P_2|^2 & 0 & d_2^2 & 1 \
d_1^2 & |P_2P_3|^2 & |P_3P_4|^2 & 1 \
|P_1P_4|^2 & d_2^2 & 0 & 1 \
1 & 1 & 1 & 0
end{array}
right|^2 , .
$$
Откуда получаем формулу
$$
2, d_1^2 d_2^2=(|P_1P_2|^2+|P_2P_3|^2+|P_3P_4|^2+|P_1P_4|^2-d_2^2) d_2^2+
$$
$$
+(|P_3P_4|^2-|P_2P_3|^2)(|P_1P_2|^2-|P_1P_4|^2)+
$$
$$
+left{
left|
begin{array}{cccc}
0 & |P_2P_3|^2 & d_2^2 & 1 \
|P_2P_3|^2 & 0 & |P_3P_4|^2 & 1 \
d_2^2 & |P_3P_4|^2 & 0 & 1 \
1 & 1 & 1 & 0
end{array}
right| cdot
left|
begin{array}{cccc}
0 & |P_1P_2|^2 & |P_1P_4|^2 & 1 \
|P_1P_2|^2 & 0 & d_2^2 & 1 \
|P_1P_4|^2 & d_2^2 & 0 & 1 \
1 & 1 & 1 & 0
end{array}
right|right}^{1/2} , ,
$$
позволяющую определить длину диагонали $ d_1 $ четырехугольника $ P_1P_2P_3P_4 $ через длину его второй диагонали и длины сторон.
Из формулы Герона далее следует:
$$
2,d_1^2 d_2^2=(|P_1P_2|^2+|P_2P_3|^2+|P_3P_4|^2+|P_1P_4|^2-d_2^2) d_2^2+
$$
$$
+ (|P_2P_3|^2-|P_3P_4|^2)(|P_1P_2|^2-|P_1P_4|^2)+
$$
$$
+16, S_{triangle P_1P_2P_3} S_{triangle P_1P_3P_4} , .
$$
Объем симплекса в $ mathbb R_{}^{n} $ с вершинами в
$$ P_1=(x_{11},x_{12},dots,x_{1n}) ,P_2=(x_{21},x_{22},dots,x_{2n}) , dots ,P_n=(x_{n1},x_{n2},dots,x_{nn}),P_{n+1}=(x_{n+1,1},x_{n+1,2},dots,x_{n+1,n}) , $$
т.е. тела, заданного уравнениями
$$
left{ X=sum_{j=1}^{n+1} alpha_j P_j big| , alpha_1ge 0,dots alpha_{n+1} ge 0, sum_{j=1}^{n+1} alpha_j =1 right}
$$
равен абсолютной величине (модулю) выражения
$$
frac{1}{n!}left| begin{array}{cllll}
1 & x_{11}& x_{12} &dots & x_{1n} \
1 & x_{21}& x_{22} & dots & x_{2n} \
vdots & & & & vdots \
1 & x_{n1}& x_{n2}& dots & x_{nn} \
1 & x_{n+1,1} & x_{n+1,2} & dots & x_{n+1,n}
end{array}
right| .
$$
Формула Кэли-Менгера для квадрата объема симплекса через длины его ребер:
$$
V^2=frac{(-1)^{n-1}}{2^n(n!)^2}
left|
begin{array}{cccccc}
0 & |P_1P_2|^2 & |P_1P_3|^2 & dots & |P_1P_{n+1}|^2 & 1 \
|P_1P_2|^2 & 0 & |P_2P_3|^2 & dots & |P_2P_{n+1}|^2 & 1 \
|P_1P_3|^2 & |P_2P_3|^2 & 0 & dots & |P_3P_{n+1}|^2 & 1 \
dots & & & & & dots \
|P_1P_{n+1}|^2 & |P_2P_{n+1}|^2 & |P_3P_{n+1}|^2 & dots & 0 & 1 \
1 & 1 & 1 & dots & 1 & 0
end{array}
right| .
$$
В частном случае: объем пирамиды
$$
left{ X=(x_1,dots,x_n) in mathbb R^n Big|
sum_{j=1}^nfrac{x_j}{a_j} le 1, x_1 ge 0,dots, x_n ge 0 right} quad npu quad a_1>0,dots,a_n>0
$$
равен
$$
frac{1}{n!}prod_{j=1}^n a_j .
$$
параллелепипеда
Объем $ n_{} $-мерного параллелепипеда в $ {mathbb R}^{n} $, построенного на вершинах
$$ (0,0,dots,0), (x_{11},x_{12},dots,x_{1n}) ,(x_{21},x_{22},dots,x_{2n}) , dots ,(x_{n1},x_{n2},dots,x_{nn}), $$
равен абсолютной величине (модулю) определителя
$$
left| begin{array}{cccc}
x_{11}& x_{12} &dots & x_{1n} \
x_{21}& x_{22} & dots & x_{2n} \
dots & & & dots \
x_{n1}& x_{n2}& dots & x_{nn}
end{array}
right| .
$$
Доказательство
☞
ЗДЕСЬ.
Объем $ m_{} $-мерного параллелепипеда в $ {mathbb R}^{n} $, построенного на вершинах
$$ (0,0,dots,0), (x_{11},x_{12},dots,x_{1n}) ,(x_{21},x_{22},dots,x_{2n}) , dots , (x_{m1},x_{m2},dots,x_{mn}), $$
равен
$$
sqrt{det(Xcdot X^{top}}) npu X=
left( begin{array}{cccc}
x_{11}& x_{12} &dots & x_{1n} \
x_{21}& x_{22} & dots & x_{2n} \
dots & & & dots \
x_{m1}& x_{m2}& dots & x_{mn}
end{array}
right) .
$$
Здесь $ {}^{top} $ означает транспонирование.
Объем $ n_{} $-мерного параллелепипеда, ограниченного плоскостями
$$
a_{j1}x_1+a_{j2}x_2+dots+a_{jn}x_n= pm h_j npu j in {1,dots, n }
$$
равен
$$
frac{2^n displaystyle prod_{j=1}^n h_j}{det[a_{jk}]_{j,k=1}^n} .
$$
эллипсоида
Объем $ n_{} $-мерного эллипсоида, ограниченного поверхностью
$$
(x_1,x_2,dots ,x_n)left( begin{array}{cccc}
a_{11} & a_{12} & dots & a_{1n} \
a_{12} & a_{22} & dots & a_{2n} \
dots & & & dots \
a_{1n} & a_{2n} & dots & a_{nn}
end{array}
right)
left(
begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right) =1
$$
(квадратичная форма, стоящая в левой части, положительно определена) равен
$$
frac{pi^{n/2}}{Gamma(frac{n}{2}+1)} frac{1}{sqrt{det [a_{jk}]_{j,k=1}^n}} .
$$
Здесь $ Gamma_{} $ обозначает гамма-функцию, при вычислениях значений которой в последней формуле достаточно пользоваться следующими ее свойствами:
$$Gamma left(frac{1}{2}right)=sqrt{pi}, Gamma(1)=Gamma(2)=1, Gamma(x+1)=xGamma(x) npu forall x >0, Gamma(n+1)=n! npu forall n in {mathbb N} . $$
П
Пример. Площадь, ограниченная эллипсом
$$ a_{11}x_{1}^2+2a_{12}x_1x_2 + a_{22}x_2^2=1 , ,$$
вычисляется по формуле
$$ frac{pi}{sqrt{a_{11}a_{22}-a_{12}^2}} . $$
Объем фигуры, ограниченной эллипсоидом
$$
(x_1,x_2,x_3)left( begin{array}{ccc}
a_{11} & a_{12} & a_{13} \
a_{12} & a_{22} & a_{23} \
a_{13} & a_{23} & a_{33}
end{array}
right)
left(
begin{array}{c}
x_1 \ x_2 \ x_3
end{array}
right) =1
$$
равен
$$
frac{4}{3} frac{pi}{sqrt{left| begin{array}{ccc}
a_{11} & a_{12} & a_{13} \
a_{12} & a_{22} & a_{23} \
a_{13} & a_{23} & a_{33}
end{array}
right|
}} .
$$
Объем фигуры, ограниченной четырехмерным эллипсоидом (в записи, аналогичной предыдущей) –
$$ frac{pi^2}{2sqrt{det(A)}} . $$
Классификация алгебраических кривых и поверхностей
Источники
[1]. Uspensky J.V. Theory of Equations. New York. McGraw-Hill. 1948
Геометрия 10-11 класс
20 баллов
Даны координаты вершин тетраэдра ABCD. Найдите: А) Площадь основания АВС. Б) Уравнение высоты тетраэдра DK. В) Уравнение прямой, проходящей через точку С параллельно высоте DK. Г) Расстояние от точки С до грани ABD. Д) Уравнение плоскости, проходящей через точки В и С перпендикулярно плоскости ABC. Е) Длину ребра BD. Ж) Объём тетраэдра ABCD. З) Величину плоского угла при вершине С плоскости BCD. И) Величину угла между ребром CD и плоскостью ABC. A(0,1,-1); B(1,2,-2); C(1,0,0); D(-1,2,0).
Ирина Каминкова
03.12.2020 13:50:11
Ответ эксперта
Ирина Каминкова
03.12.2020 13:50:39
Ответ эксперта
Ирина Каминкова
03.12.2020 13:51:06
Ответ эксперта
Ирина Каминкова
03.12.2020 13:51:31
Ответ эксперта
Все предметы
Рейтинг пользователей
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Найдите площадь сечения правильного тетраэдра PABC плоскостью, параллельной рёбрам PA и PC и проходящей через середину ребра PB, если все рёбра тетраэдра равны 8.
2
Найдите площадь сечения правильного тетраэдра PABC плоскостью, параллельной рёбрам PA и PC и проходящей через середину ребра PB, если все рёбра тетраэдра равны 4.
Аналоги к заданию № 488: 489 Все
3
Найдите площадь сечения правильного тетраэдра PABC плоскостью, проходящей через середины рёбер BC и PC параллельно ребру AC, если все рёбра тетраэдра равны 10.
4
Найдите площадь сечения правильного тетраэдра PABC плоскостью, проходящей через середины рёбер BC и PC параллельно ребру AC, если все рёбра тетраэдра равны 6.
Аналоги к заданию № 490: 491 Все
5
Найдите площадь сечения правильного тетраэдра PABC плоскостью, проходящей через точки, делящие рёбра PC и BC в отношении считая от вершины C, параллельно ребру BP, если все рёбра тетраэдра равны 3.
Пройти тестирование по этим заданиям