
{S = dfrac{1}{2} (a + b) cdot h}
Площадь трапеции можно найти множеством способов. Для вас мы собрали все возможные варианты нахождения площади. Для вашего удобства для каждой формулы создан калькулятор, который поможет рассчитать площадь трапеции по известным данным. От вас требуется только подставить значения и в режиме онлайн мгновенно получить ответ. Формулы и калькуляторы сгруппированы по типам трапеций – обычная, равнобедренная (равнобокая).
- Калькулятор площади трапеции
- Площадь трапеции
- через основания и высоту
- через среднюю линию и высоту
- через диагонали и среднюю линию
- через 4 стороны
- через диагонали и угол между ними
- через основания и углы при основании
- через площади треугольников
- через диагонали и высоту
- через радиус вписанной окружности и основания
- через перпендикулярные диагонали
- Площадь равнобедренной (равнобокой) трапеции
- через основания и высоту
- через 3 стороны (формула Брахмагупты)
- через верхнее основание, боковую сторону и угол при нижнем основании
- через нижнее основание, боковую сторону и угол при нижнем основании
- через основания и угол
- через диагонали и угол между ними
- через боковую сторону, угол при основании и среднюю линию
- через радиус вписанной окружности и угол при основании
- Площадь равнобедренной (равнобокой) трапеции, в которую можно вписать окружность
- через высоту (диаметр вписанной окружности) и угол при основании
- через основания и угол при основании
- через основания и радиус вписанной окружности
- через основания
- через основания и боковую сторону
- через основания и среднюю линию
- Примеры задач
Площадь трапеции
Трапеция — выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Площадь трапеции через основания и высоту
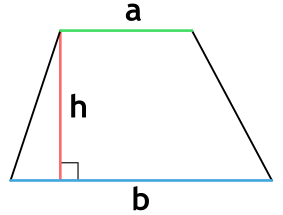
{S = dfrac{1}{2} (a + b) cdot h}
a и b – основания трапеции
h – высота, проведенная к основанию
Площадь трапеции через среднюю линию и высоту
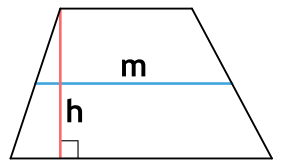
{S = m cdot h}
m – средняя линия трапеции
h – высота трапеции
Площадь трапеции через диагонали и среднюю линию
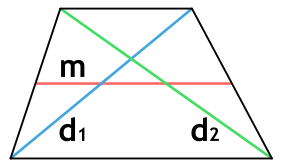
{S = sqrt{p(p-d_1)(p-d_2)(p-2m)}}
{p = dfrac{d_1+d_2+2m}{2}}
d1 и d2 – диагонали трапеции
m – средняя линия трапеции
Площадь трапеции через 4 стороны
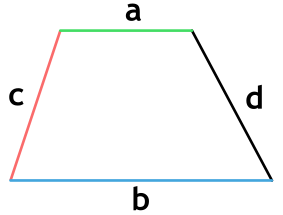
{S = dfrac{a+b}{2} sqrt{c^2 – {Big( dfrac{(a-b)^2 + c^2 – d^2}{2(a-b)} Big)}^2}}
a, b, c и d – стороны трапеции
Площадь трапеции через диагонали и угол между ними
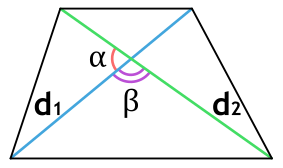
{S = dfrac{d_1 cdot d_2}{2}cdot sin(alpha); S = dfrac{d_1 cdot d_2}{2}cdot sin(beta)}
d1 и d2 – диагонали трапеции
α или β – угол между диагоналями трапеции
Площадь трапеции через основания и углы при основании
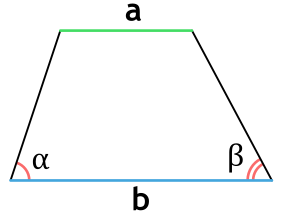
{S = dfrac{b^2 – a^2}{2} cdot dfrac{sin(alpha) cdot sin(beta)}{sin(alpha + beta)}}
a и b – основания трапеции
α или β – прилежащие к основанию трапеции углы
Площадь трапеции через площади треугольников
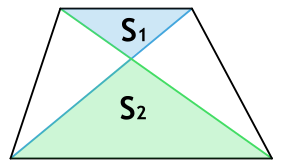
{S = (sqrt{S_1} + sqrt{S_2})^2}
S1 и S2 – площади образованных пересечением диагоналей трапеции треугольников
Площадь трапеции через диагонали и высоту
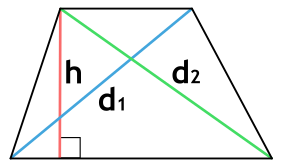
{S = dfrac{sqrt{{d_2}^2-h^2}+sqrt{{d_1}^2-h^2}}{2} cdot h}
d1 и d2 – диагонали трапеции
h – высота трапеции
Площадь трапеции через радиус вписанной окружности и основания

{S = (a+b)cdot r}
a и b – основания трапеции
r – радиус вписанной в трапецию окружности
Площадь трапеции через перпендикулярные диагонали

{S = dfrac{1}{2} cdot d_1 cdot d_2}
d1 и d2 – перпендикулярные диагонали трапеции
Площадь равнобедренной (равнобокой) трапеции
Равнобедренная трапеция — это трапеция, у которой боковые стороны равны.
Площадь равнобедренной трапеции через основания и высоту
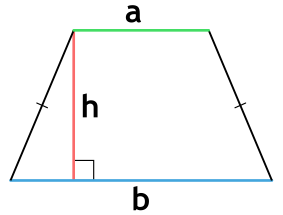
{S = dfrac{a+b}{2} cdot h}
a и b – основания равнобедренной трапеции
h – высота, проведенная к основанию равнобедренной трапеции
Площадь равнобедренной трапеции через 3 стороны (формула Брахмагупты)

{S = sqrt{(p-a)(p-b)(p-c)^2}}
{p = dfrac{a+b+2c}{2}}
a и b – основания равнобедренной трапеции
c – боковая сторона равнобедренной трапеции
Площадь равнобедренной трапеции через верхнее основание, боковую сторону и угол при нижнем основании

{S = c cdot sin(alpha) cdot (a+c cdot cos(alpha))}
a – верхнее основание равнобедренной трапеции
c – боковая сторона равнобедренной трапеции
α – прилежащие к нижнему основанию трапеции углы
Площадь равнобедренной трапеции через нижнее основание, боковую сторону и угол при нижнем основании
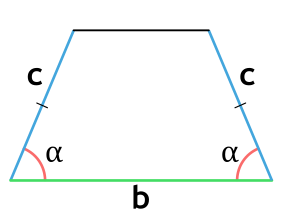
{S = c cdot sin(alpha) cdot (b-c cdot cos(alpha))}
b – нижнее основание равнобедренной трапеции
c – боковая сторона равнобедренной трапеции
α – прилежащий к нижнему основанию трапеции угол
Площадь равнобедренной трапеции через основания и угол
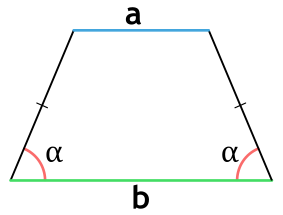
{S = dfrac{1}{2}(b^2-a^2) cdot tg(alpha)}
a и b – основания равнобедренной трапеции
α – прилежащий к основанию трапеции угол
Площадь равнобедренной трапеции через диагонали и угол между ними
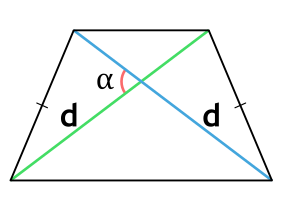
{S = dfrac{1}{2}d^2 cdot sin(alpha)}
a – диагональ равнобедренной трапеции
α – угол между диагоналями равнобедренной трапеции
Площадь равнобедренной трапеции через боковую сторону, угол при основании и среднюю линию
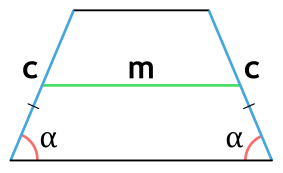
{S = m cdot c cdot sin(alpha)}
m – средняя линия равнобедренной трапеции
c – боковая сторона равнобедренной трапеции
α – угол при основании равнобедренной трапеции
Площадь равнобедренной трапеции через радиус вписанной окружности и угол при основании

{S = dfrac{4r^2}{sin(alpha)}}
r – радиус вписанной окружности
α – угол при основании равнобедренной трапеции
Площадь равнобедренной (равнобокой) трапеции, в которую можно вписать окружность
В трапецию можно вписать окружность тогда и только тогда, когда суммы ее противоположных сторон равны.
Площадь равнобедренной трапеции, в которую можно вписать окружность, через высоту (диаметр вписанной окружности) и угол при основании

{S = dfrac{h^2}{sin(alpha)}}
h – высота равнобедренной трапеции
α – угол при основании равнобедренной трапеции
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и угол при основании
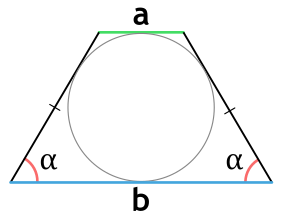
{S = dfrac{a cdot b}{sin(alpha)}}
a и b – основания равнобедренной трапеции
α – угол при основании равнобедренной трапеции
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и радиус вписанной окружности
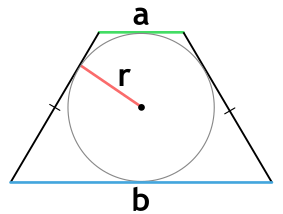
{S = r(a+b); r=dfrac{sqrt{a cdot b}}{2}}
a и b – основания равнобедренной трапеции
r – радиус вписанной окружности
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания

{S = sqrt{a cdot b} cdot dfrac{a+b}{2}}
a и b – основания равнобедренной трапеции
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и боковую сторону
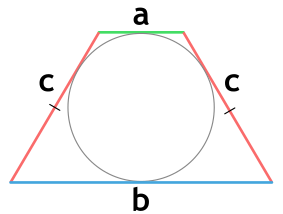
{S = c cdot sqrt{a cdot b}}
a и b – основания равнобедренной трапеции
c – боковая сторона равнобедренной трапеции
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и среднюю линию
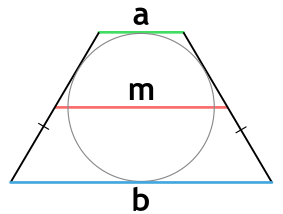
{S = m cdot sqrt{a cdot b}}
a и b – основания равнобедренной трапеции
m – средняя линия равнобедренной трапеции
Примеры задач на нахождение площади трапеции
Задача 1
Найдите площадь трапеции, если основания равны 6см и 9 см, а высота трапеции равна 5 см.
Решение
Для решения задачи воспользуемся первой формулой.
S = dfrac{1}{2} (a + b) cdot h = dfrac{1}{2} (6 + 9) cdot 5 = dfrac{1}{2} cdot 15 cdot 5 = dfrac{1}{2} cdot 75 = 37dfrac{1}{2} : см^2
Ответ: 37.5 см²
Полученный ответ легко проверить с помощью калькулятора .
Задача 2
Найдите площадь трапеции средняя линия которой равна 18 см, а высота 9 см.
Решение
С решением этой задачи нам поможет вторая формула.
S = m cdot h = 18 cdot 9 = 162 : см^2
Ответ: 162 см²
Воспользуемся калькулятором для проверки результата.
Задача 3
Найдите площадь трапеции диагонали которой равны 10 и 8, а средняя линия равна 3.
Решение
Для решения этой задачи нам поможет третья формула.
На первом этапе вычислим p:
p = dfrac{d_1+d_2+2m}{2} = dfrac{10+8+2 cdot 3}{2} = dfrac{10+8+6}{2} = dfrac{24}{2} = 12
А теперь можно вычислить площадь трапеции:
S = sqrt{p(p-d_1)(p-d_2)(p-2m)} = sqrt{12(12-10)(12-8)(12-2 cdot 3)} = sqrt{12 cdot 2 cdot 4 cdot 6} = sqrt{576} = 24 : см^2
Ответ: 24 см²
Осталось проверить полученный ответ.
Задача 4
Найдите площадь трапеции диагонали которой равны 17 и 15, а средняя линия равна 4.
Решение
Задача похожа на ту, что мы только что решили. Поэтому повторим шаги.
На первом этапе вычислим p:
p = dfrac{d_1+d_2+2m}{2} = dfrac{17+15+ 2 cdot 4}{2} = dfrac{17+15+8}{2} = dfrac{40}{2} = 20
А теперь можно вычислить площадь трапеции:
S = sqrt{p(p-d_1)(p-d_2)(p-2m)} = sqrt{20(20-17)(20-15)(20-2 cdot 4)} = sqrt{20 cdot 3 cdot 5 cdot 12} = sqrt{3600} = 60 : см^2
Ответ: 60 см²
Проверка .
Задача 5
Найдите площадь трапеции диагонали которой равны 8 и 6 а средняя линия равна 5.
Решение
Еще одна типовая задача. Повторим действия как в задачах выше.
На первом этапе вычислим p:
p = dfrac{d_1+d_2+2m}{2} = dfrac{8+6+ 2 cdot 5}{2} = dfrac{8+6+10}{2} = dfrac{24}{2} = 12
А теперь можно вычислить площадь трапеции:
S = sqrt{p(p-d_1)(p-d_2)(p-2m)} = sqrt{12(12-8)(12-6)(12-2 cdot 5)} = sqrt{12 cdot 4 cdot 6 cdot 2} = sqrt{576} = 24 : см^2
Ответ: 24 см²
Проверка .
Задача 6
Найдите площадь равнобедренной трапеции если её основания равны 5 см и 17 см, а боковая сторона равна 10 см.
Решение
Для решения этой задачи используем формулу Брахмагупты.
Сначала вычислим p:
p = dfrac{a+b+2c}{2} = dfrac{5+17+2 cdot 10}{2} = dfrac{22+20}{2} = dfrac{42}{2} = 21
А теперь можно вычислить площадь трапеции:
S = sqrt{(p-a)(p-b)(p-c)^2} = sqrt{(21-5)(21-17)(21-10)^2} = sqrt{16 cdot 4 cdot 11^2} = sqrt{16 cdot 4 cdot 121} = sqrt{7744}= 88 : см^2
Ответ: 88 см²
Проверка .
Задача 7
Острый угол равнобедренной трапеции равен 45°, а основания равны 8 и 6 см. Найдите площадь трапеции.
Решение
Для решения этой задачи воспользуемся формулой.
S = dfrac{1}{2}(b^2-a^2) cdot tg(alpha) = dfrac{1}{2}(8^2-6^2) cdot tg(45°)
Тангенс 45° = 1, продолжим вычисления:
S = dfrac{1}{2}(8^2-6^2) cdot tg(45°) = dfrac{1}{2}(64-36) cdot 1 = dfrac{1}{2} cdot 28 = 14 : см^2
Ответ: 14 см²
Убедиться в правильности решения нам поможет калькулятор .
Лучший ответ
Семен Аркадьевич
Высший разум
(340149)
10 лет назад
Элементарно.. .
Зная соотношение площадей, определяем соотношение отрезков, нпа котрые делятся диагонали точкой пересечения.
Зная соотношение отрезков, находим площади треугольников, премыкающих к боковым сторонам. 
Остальные ответы
Павел Жуков
Гуру
(4822)
10 лет назад
Если равнобедренные, полторы площади каждого треугольника сложить.
Smet Smet
Профи
(606)
10 лет назад
Какие именно треугольники надо указывать. В общем случае не будет решения.
Лариса Скугорова
Знаток
(300)
6 лет назад
Как найти площадь трапеции если извесные площади треугольников s2 и s4.
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Площадь
- Площадь трапеции
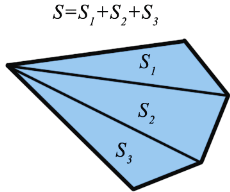
Для вычисления площади произвольного многоугольника его разбивают на треугольники и находят площадь каждого из них. Площадь данного многоугольника равна сумме площадей этих треугольников.
Условимся называть высотой трапеции перпендикуляр, который проведен из любой точки одного из оснований к прямой, содержащей другое основание.
Теорема
Площадь трапеции равна произведению полусуммы ее оснований на высоту
Доказательство
Дано: ABCD – трапеция, BH и DH1 – высоты, S – площадь
Доказать: S = 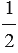 (AD + BC)
(AD + BC)  ВН
ВН
Доказательство:
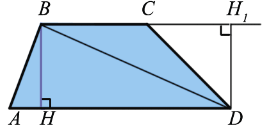
Диагональ BD разделяет трапецию на два треугольника ABD и BCD, поэтому S = SABD + SBCD. Примем отрезки AD и ВН за основание и высоту треугольника ABD, а отрезки BC и DH1 за основание и высоту треугольника BCD. Тогда
SABD = 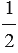 AD
AD  BH, SBCD =
BH, SBCD = 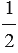 BC
BC  DH1.
DH1.
Так как DH1 = BH, то SBCD = 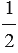 BC
BC  BH.
BH.
Таким образом,
S = 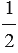 AD
AD  BH +
BH + 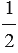 BC
BC  BH =
BH = 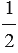 (AD + BC)
(AD + BC)  BH.
BH.
Теорема доказана.
Советуем посмотреть:
Понятие площади многоугольника
Площадь квадрата
Площадь прямоугольника
Площадь параллелограмма
Площадь треугольника
Теорема Пифагора
Теорема, обратная теореме Пифагора
Формула Герона
Площадь
Правило встречается в следующих упражнениях:
7 класс
Задание 480,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 495,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 512*,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 518,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 527,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 621,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 725,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 735,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 892,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1070,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Преподаватель который помогает студентам и школьникам в учёбе.
Площадь трапеции – определение и вычисление с примерами решения
Теорема (о площади трапеции). Площадь трапеции равна произведению полусуммы ее оснований на высоту.
Доказательство:
Пусть 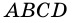
Докажем, что площадь 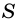 трапеции можно найти по формуле:
трапеции можно найти по формуле:
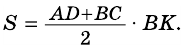
1) Диагональ 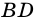 разбивает трапецию на два треугольника
разбивает трапецию на два треугольника 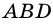 и
и 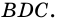 Поэтому
Поэтому 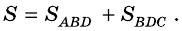
2) 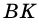 – высота треугольника
– высота треугольника 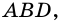 поэтому
поэтому 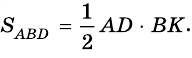
3) Проведем в трапеции высоту 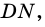 она является и высотой треугольника
она является и высотой треугольника 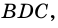 поэтому
поэтому 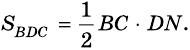
4) 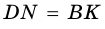 (как высоты трапеции). Следовательно,
(как высоты трапеции). Следовательно,
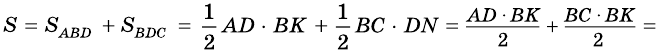
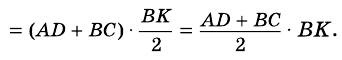
В общем виде формулу площади 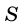 трапеции можно записать так:
трапеции можно записать так:
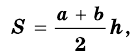
где 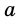 и
и 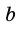 – основания трапеции,
– основания трапеции, 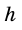 – ее высота.
– ее высота.
Следствие. Площадь трапеции равна произведению ее средней линии на высоту.
Пример:
В трапеции 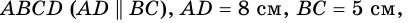
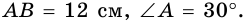 Найдите площадь трапеции.
Найдите площадь трапеции.
Решение:
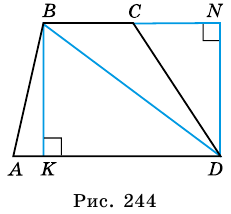
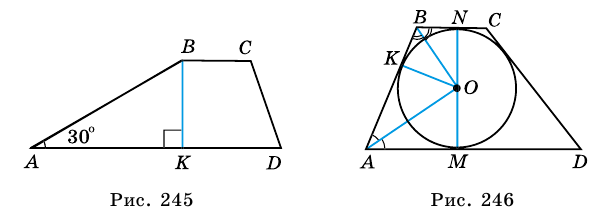
1) Проведем в трапеции 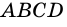 высоту
высоту 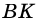
(рис. 245). В 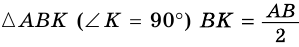 (по свойству катета, противолежащего углу 30°). Следовательно,
(по свойству катета, противолежащего углу 30°). Следовательно, 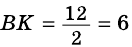 (см).
(см).
2) 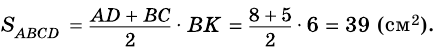
Ответ. 39 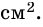
Пример:
Периметр трапеции 60 см, а одна из боковых сторон точкой касания вписанной окружности делится на отрезки 9 см и 4 см. Найдите площадь трапеции.
Решение:
1) Так как трапеция является описанной около окружности (рис. 246), то
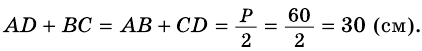
2) Центр вписанной окружности – точка  – является точкой пересечения биссектрис углов трапеции, следовательно, и углов
– является точкой пересечения биссектрис углов трапеции, следовательно, и углов 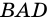 и
и 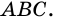 Поэтому
Поэтому 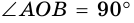 (задача 214, с. 43).
(задача 214, с. 43).
3) Точка 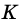 – точка касания окружности со стороной
– точка касания окружности со стороной 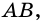 поэтому
поэтому 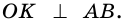 Следовательно,
Следовательно, 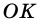 – радиус окружности и высота прямоугольного треугольника
– радиус окружности и высота прямоугольного треугольника 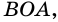 проведенная к гипотенузе. По теореме о средних пропорциональных отрезках в прямоугольном треугольнике имеем:
проведенная к гипотенузе. По теореме о средних пропорциональных отрезках в прямоугольном треугольнике имеем: 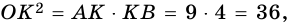 откуда
откуда 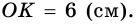
4) 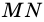 — диаметр окружности, а также высота трапеции, поэтому
— диаметр окружности, а также высота трапеции, поэтому 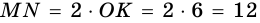 (см).
(см).
5) Следовательно, 
Ответ. 180 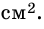
Площадь трапеции
Часто для вычисления площади некоторого многоугольника его разбивают на несколько треугольников и находят искомую площадь как сумму площадей этих треугольников. Именно такой подход можно применить для вывода формулы площади трапеции.
Теорема (формула площади трапеции) Площадь трапеции равна произведению полусуммы ее оснований на высоту:
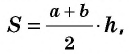
где 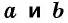 — основания трапеции,
— основания трапеции, 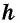 — высота трапеции.
— высота трапеции.
Доказательство:
Пусть дана трапеция 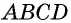 с основаниями
с основаниями 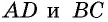 и высотой
и высотой 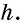 Диагональ
Диагональ 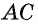 делит ее на два треугольника
делит ее на два треугольника 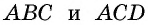 (рис. 151).
(рис. 151).
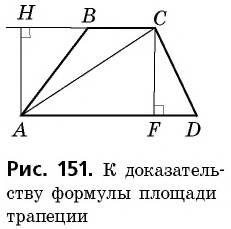
Проведем высоты этих треугольников 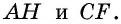 Обе они являются высотами трапеции, т.е. равны
Обе они являются высотами трапеции, т.е. равны 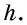 Имеем:
Имеем:
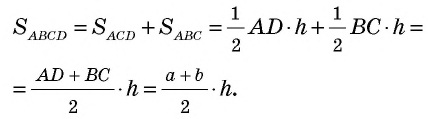
Теорема доказана.
Следствие
Площадь трапеции равна произведению средней линии на высоту.
- Центральные и вписанные углы
- Углы и расстояния в пространстве
- Подобие треугольников
- Решение прямоугольных треугольников
- Прямоугольник и его свойства
- Ромб и его свойства, определение и примеры
- Квадрат и его свойства
- Трапеция и ее свойства
Выбирайте формулу в зависимости от известных величин.
1. Как найти площадь трапеции через основания и высоту
Посчитайте сумму оснований трапеции.
Умножьте результат на высоту и поделите на два.
- S – искомая площадь трапеции.
- a и b – основания трапеции (её параллельные стороны).
- h – высота трапеции.
2. Как вычислить площадь трапеции через высоту и среднюю линию
Просто умножьте высоту трапеции на среднюю линию.
- S – искомая площадь трапеции.
- m – средняя линия трапеции (отрезок, соединяющий середины боковых сторон).
- h – высота трапеции.
3. Как найти площадь трапеции через диагонали и угол между ними
Умножьте одну диагональ на другую, а затем — на синус любого угла между ними.
Поделите результат на два.
- S – искомая площадь трапеции.
- x и y – диагонали трапеции.
- α – любой угол между диагоналями.
4. Как найти площадь трапеции через четыре стороны
Отнимите от большего основания меньшее.
Найдите квадрат полученного числа.
Прибавьте к результату квадрат одной боковой стороны и отнимите квадрат второй.
Поделите полученное число на удвоенную разность оснований.
Найдите квадрат результата и отнимите его от квадрата боковой стороны.
Найдите корень из полученного числа.
Умножьте результат на половину от суммы оснований.
- S – искомая площадь трапеции.
- a, b – основания трапеции.
- c, d – боковые стороны.
5. Как вычислить площадь равнобедренной трапеции через четыре стороны
Отнимите от большего основания трапеции меньшее и поделите результат на два.
Найдите квадрат полученного числа и отнимите его от квадрата боковой стороны.
Найдите корень из результата.
Умножьте полученное число на сумму оснований и поделите на два.
- S — искомая площадь трапеции.
- a, b — основания трапеции.
- c, d — боковые стороны (напомним, в равнобедренной трапеции они равны).
6. Как найти площадь равнобедренной трапеции через радиус вписанной окружности и угол
Найдите квадрат радиуса и умножьте его на четыре.
Поделите результат на синус известного угла.
- r — радиус вписанной окружности.
- α — любой угол трапеции.
Читайте также 📐✏️🎓
- 8 способов найти длину окружности
- 8 способов найти периметр треугольника
- 7 способов найти площадь прямоугольника
- Как перевести обычную дробь в десятичную
- Как освоить устный счёт школьникам и взрослым

