Как найти площадь трапеции через синус угла - Сайт, где вы сможете решить свои вопросы

Площадь трапеции, формулы расчета, определение,
способы найти площадь, нахождение площади
через величины и примеры площади трапеции.

Все формулы расчета площади трапеции
через основания и угол, периметр, радиус,
синус и две стороны, диагональ,
высоту, среднюю линию.

Площадь трапеции, можно измерить, в единицах
измерения в квадрате: мм², см², м² и км² и так далее.

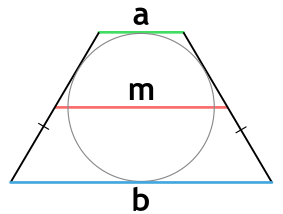
Площадь трапеции через окружность вписанную можно
найти, зная радиус окружности вписанной в трапецию
и некоторые другие величины.

Содержание

Формулы площади трапеции
Площадь любых трапеций
Площадь равнобедренной трапеции
Определения трапеции
Элементы трапеции

Формулы площади трапеции

Площадь любых трапеций

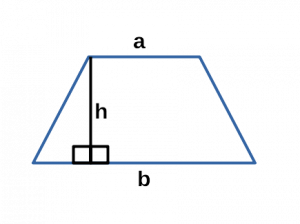
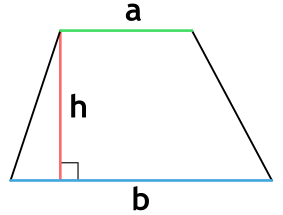
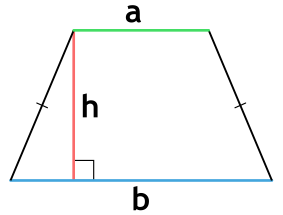
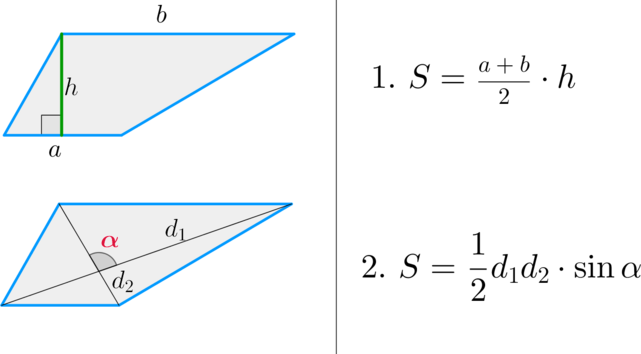
Ⅰ. Площадь трапеции через основания и высоту:

[ S = frac{a+b}{2} cdot h ]
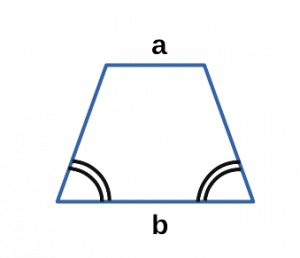
a,b — основания трапеции;
h — высота трапеции;

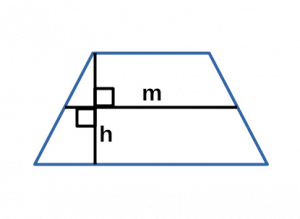
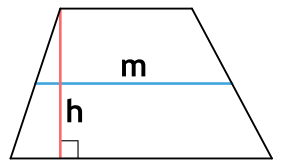
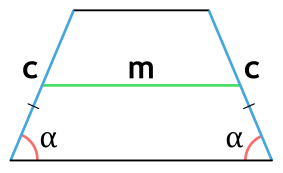
Ⅱ. Площадь трапеции через высоту и среднюю линию:

[ S = mh ]
m — средняя линия трапеции;
h — высота трапеции;

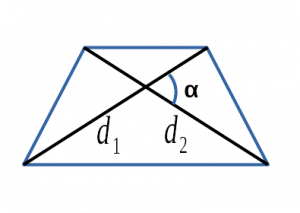
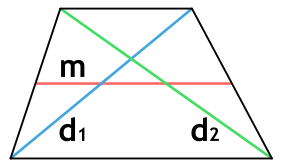
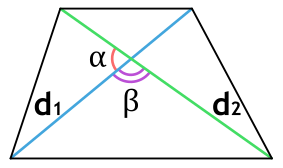
Ⅲ. Площадь трапеции через диагонали и угол между ними:

[ S =frac{1}{2}d_1d_2 cdot sin alpha ]
( d_1, d_2 )- диагонали трапеции;
sin α — синус угла альфа в трапеции;

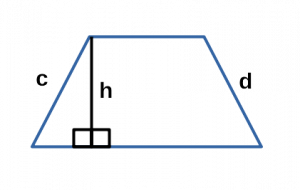
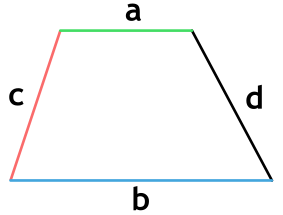
Ⅳ. Площадь трапеции через периметр, высоту и боковые стороны:

[ S = frac{P-(c+d)}{2}h ]
P — периметр трапеции;
c,d — боковые стороны трапеции;
h — высота трапеции;

Ⅴ. Площадь трапеции через основания и боковые стороны:
[ S = frac{a+b}{2} cdot sqrt{c^2-(frac{(a+b)^2+c^2-d^2}{2a-2b})^2} ]
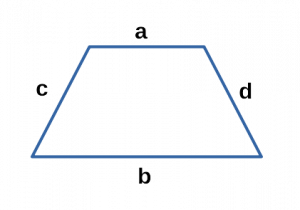
a,b — основания трапеции;
с,d — боковые стороны трапеции;

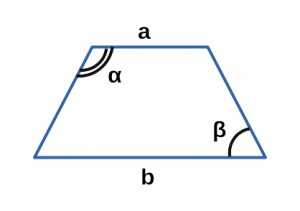
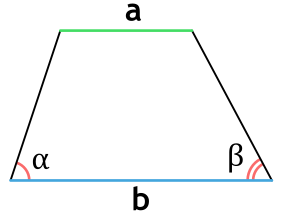
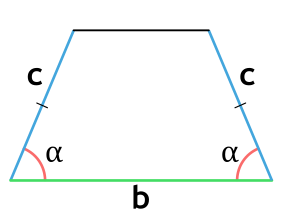
Ⅵ. Площадь трапеции через основания и углы:

[ S = frac{b^2-a^2}{2} cdot frac{sin α cdot sin β}{sin( α + β)} ]

a,b — основания трапеции;
α — угол при основании a в трапеции;
β — угол при основании b в трапеции;
sin α — синус угла альфа в трапеции;
sin β — синус угла бетта в трапеции;

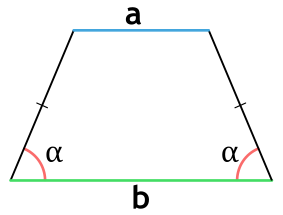
Площадь равнобедренной трапеции

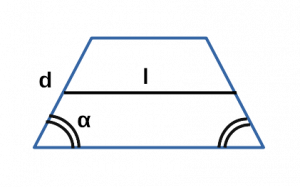
Ⅰ. Площадь трапеции через синус угла, среднюю линию и боковую сторону:

[ S = ld cdot sin α ]

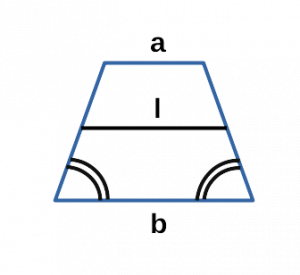
l — средняя линия равнобедренной трапеции;
d — боковая сторона равнобедренной трапеции;
α — угол альфа при боковой стороне d равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;

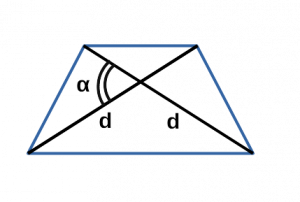
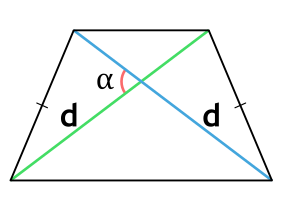
Ⅱ. Площадь трапеции через диагонали и синус угла:

[ S = frac{d^2}{2} cdot sin α ]

d — диагональ равнобедренной трапеции;
α — угол между двумя диагоналями в равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;

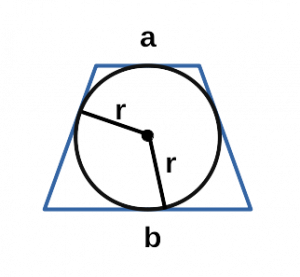
Ⅲ. Площадь трапеции через радиус вписанной окружности и основания:

[ S = r( a+b) ]

r — радиус вписанной окружности равнобедренной трапеции;
a, b — основания равнобедренной трапеции;

Ⅳ. Площадь трапеции через основания:

[ S = sqrt{ab} cdot {frac{a+b}{2}} ]

a, b — основания равнобедренной трапеции;

Ⅴ. Площадь трапеции через основания и среднюю линию:

[ S = lsqrt{ab} ]

l — средняя линия равнобедренной трапеции;
a, b — основания равнобедренной трапеции;

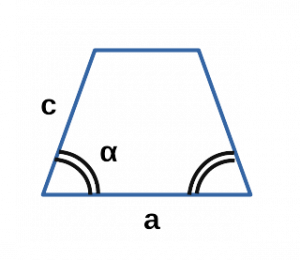
Ⅵ. Площадь трапеции через синус угла и стороны:

[ S = c cdot sin α cdot (a-c cdot cos α) ]

a — нижнее основание равнобедренной трапеции;
с — боковая сторона равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;
cos α — косинус угла альфа в равнобедренной трапеции;

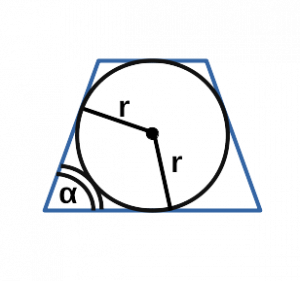
Ⅶ. Площадь трапеции через угол и радиус вписанной окружности:

[ S = frac{4r^2}{sin α} ]

r — радиус вписанной окружности равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;

Определения трапеции

Трапеция — это четырехугольник, у которого две
стороны параллельны а две другие нет.

Зная углы трапеции, можно определить, к какому виду
она относится. Всего различают три вида трапеций:

Обычная / стандартная трапеция: четыре угла и четыре стороны не равны.
Равнобедренная / равнобочная / равнобоковая трапеция:
два угла при основании равны, две боковые стороны равны.
Прямоугольная / прямая трапеция: один из углов прямой.

Площадь равнобедренной, прямоугольной трапеции,
можно найти через формулы площади обычной трапеции.

Формул, с помощью которых, можно найти площадь трапеции
через описанную окружность около трапеции, не существует.

Элементы трапеции

Любая трапеция является четырехугольником,
поэтому у трапеции 4 угла и 4 стороны.

Основание трапеции — это сторона, противолежащая
сторона которой параллельна.

Боковая сторона трапеции — это сторона, противолежащая
сторона которой не параллельна.

Средняя линия трапеции — это отрезок, соединяющий
середины боковых сторон трапеции.

Диагональ трапеции — это отрезок, соединяющий две
вершины, которые лежат в разных концах трапеции.

Высота трапеции — это отрезок, соединяющий меньшее основание с большим,
образуя при этом два угла по 90 градусов на большей стороне.

Основания у трапеции не могут быть никогда равны.
Боковые стороны могут быть равны только,
если трапеция — равнобедренная.

Площадь трапеции — это площадь геометрической фигуры,
у которой четыре стороны и четыре угла, причем только
две стороны параллельны а остальные нет.

Источник

{S = dfrac{1}{2} (a + b) cdot h}

Площадь трапеции можно найти множеством способов. Для вас мы собрали все возможные варианты нахождения площади. Для вашего удобства для каждой формулы создан калькулятор, который поможет рассчитать площадь трапеции по известным данным. От вас требуется только подставить значения и в режиме онлайн мгновенно получить ответ. Формулы и калькуляторы сгруппированы по типам трапеций – обычная, равнобедренная (равнобокая).

Калькулятор площади трапеции
Площадь трапеции
1. через основания и высоту
2. через среднюю линию и высоту
3. через диагонали и среднюю линию
4. через 4 стороны
5. через диагонали и угол между ними
6. через основания и углы при основании
7. через площади треугольников
8. через диагонали и высоту
9. через радиус вписанной окружности и основания
10. через перпендикулярные диагонали
Площадь равнобедренной (равнобокой) трапеции
1. через основания и высоту
2. через 3 стороны (формула Брахмагупты)
3. через верхнее основание, боковую сторону и угол при нижнем основании
4. через нижнее основание, боковую сторону и угол при нижнем основании
5. через основания и угол
6. через диагонали и угол между ними
7. через боковую сторону, угол при основании и среднюю линию
8. через радиус вписанной окружности и угол при основании
Площадь равнобедренной (равнобокой) трапеции, в которую можно вписать окружность
1. через высоту (диаметр вписанной окружности) и угол при основании
2. через основания и угол при основании
3. через основания и радиус вписанной окружности
4. через основания
5. через основания и боковую сторону
6. через основания и среднюю линию
Примеры задач

Площадь трапеции

Трапеция — выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

Площадь трапеции через основания и высоту

{S = dfrac{1}{2} (a + b) cdot h}

a и b – основания трапеции

h – высота, проведенная к основанию

Площадь трапеции через среднюю линию и высоту

{S = m cdot h}

m – средняя линия трапеции

h – высота трапеции

Площадь трапеции через диагонали и среднюю линию

{S = sqrt{p(p-d_1)(p-d_2)(p-2m)}}
{p = dfrac{d_1+d_2+2m}{2}}

d₁ и d₂ – диагонали трапеции

m – средняя линия трапеции

Площадь трапеции через 4 стороны

{S = dfrac{a+b}{2} sqrt{c^2 – {Big( dfrac{(a-b)^2 + c^2 – d^2}{2(a-b)} Big)}^2}}

a, b, c и d – стороны трапеции

Площадь трапеции через диагонали и угол между ними

{S = dfrac{d_1 cdot d_2}{2}cdot sin(alpha); S = dfrac{d_1 cdot d_2}{2}cdot sin(beta)}

d₁ и d₂ – диагонали трапеции

α или β – угол между диагоналями трапеции

Площадь трапеции через основания и углы при основании

{S = dfrac{b^2 – a^2}{2} cdot dfrac{sin(alpha) cdot sin(beta)}{sin(alpha + beta)}}

a и b – основания трапеции

α или β – прилежащие к основанию трапеции углы

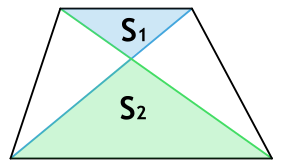
Площадь трапеции через площади треугольников

{S = (sqrt{S_1} + sqrt{S_2})^2}

S₁ и S₂ – площади образованных пересечением диагоналей трапеции треугольников

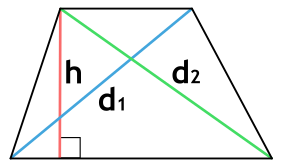
Площадь трапеции через диагонали и высоту

{S = dfrac{sqrt{{d_2}^2-h^2}+sqrt{{d_1}^2-h^2}}{2} cdot h}

d₁ и d₂ – диагонали трапеции

h – высота трапеции

Площадь трапеции через радиус вписанной окружности и основания

{S = (a+b)cdot r}

a и b – основания трапеции

r – радиус вписанной в трапецию окружности

Площадь трапеции через перпендикулярные диагонали

{S = dfrac{1}{2} cdot d_1 cdot d_2}

d₁ и d₂ – перпендикулярные диагонали трапеции

Площадь равнобедренной (равнобокой) трапеции

Равнобедренная трапеция — это трапеция, у которой боковые стороны равны.

Площадь равнобедренной трапеции через основания и высоту

{S = dfrac{a+b}{2} cdot h}

a и b – основания равнобедренной трапеции

h – высота, проведенная к основанию равнобедренной трапеции

Площадь равнобедренной трапеции через 3 стороны (формула Брахмагупты)

{S = sqrt{(p-a)(p-b)(p-c)^2}}
{p = dfrac{a+b+2c}{2}}

a и b – основания равнобедренной трапеции

c – боковая сторона равнобедренной трапеции

Площадь равнобедренной трапеции через верхнее основание, боковую сторону и угол при нижнем основании

{S = c cdot sin(alpha) cdot (a+c cdot cos(alpha))}

a – верхнее основание равнобедренной трапеции

c – боковая сторона равнобедренной трапеции

α – прилежащие к нижнему основанию трапеции углы

Площадь равнобедренной трапеции через нижнее основание, боковую сторону и угол при нижнем основании

{S = c cdot sin(alpha) cdot (b-c cdot cos(alpha))}

b – нижнее основание равнобедренной трапеции

c – боковая сторона равнобедренной трапеции

α – прилежащий к нижнему основанию трапеции угол

Площадь равнобедренной трапеции через основания и угол

{S = dfrac{1}{2}(b^2-a^2) cdot tg(alpha)}

a и b – основания равнобедренной трапеции

α – прилежащий к основанию трапеции угол

Площадь равнобедренной трапеции через диагонали и угол между ними

{S = dfrac{1}{2}d^2 cdot sin(alpha)}

a – диагональ равнобедренной трапеции

α – угол между диагоналями равнобедренной трапеции

Площадь равнобедренной трапеции через боковую сторону, угол при основании и среднюю линию

{S = m cdot c cdot sin(alpha)}

m – средняя линия равнобедренной трапеции

c – боковая сторона равнобедренной трапеции

α – угол при основании равнобедренной трапеции

Площадь равнобедренной трапеции через радиус вписанной окружности и угол при основании

{S = dfrac{4r^2}{sin(alpha)}}

r – радиус вписанной окружности

α – угол при основании равнобедренной трапеции

Площадь равнобедренной (равнобокой) трапеции, в которую можно вписать окружность

В трапецию можно вписать окружность тогда и только тогда, когда суммы ее противоположных сторон равны.

Площадь равнобедренной трапеции, в которую можно вписать окружность, через высоту (диаметр вписанной окружности) и угол при основании

{S = dfrac{h^2}{sin(alpha)}}

h – высота равнобедренной трапеции

α – угол при основании равнобедренной трапеции

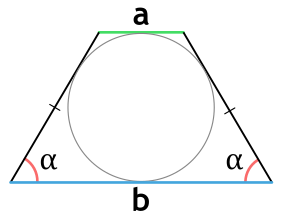
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и угол при основании

{S = dfrac{a cdot b}{sin(alpha)}}

a и b – основания равнобедренной трапеции

α – угол при основании равнобедренной трапеции

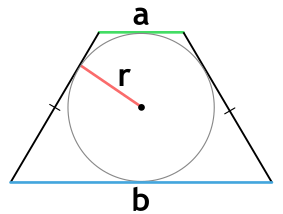
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и радиус вписанной окружности

{S = r(a+b); r=dfrac{sqrt{a cdot b}}{2}}

a и b – основания равнобедренной трапеции

r – радиус вписанной окружности

Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания

{S = sqrt{a cdot b} cdot dfrac{a+b}{2}}

a и b – основания равнобедренной трапеции

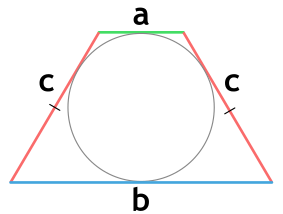
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и боковую сторону

{S = c cdot sqrt{a cdot b}}

a и b – основания равнобедренной трапеции

c – боковая сторона равнобедренной трапеции

Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и среднюю линию

{S = m cdot sqrt{a cdot b}}

a и b – основания равнобедренной трапеции

m – средняя линия равнобедренной трапеции

Примеры задач на нахождение площади трапеции

Задача 1

Найдите площадь трапеции, если основания равны 6см и 9 см, а высота трапеции равна 5 см.

Решение

Для решения задачи воспользуемся первой формулой.

S = dfrac{1}{2} (a + b) cdot h = dfrac{1}{2} (6 + 9) cdot 5 = dfrac{1}{2} cdot 15 cdot 5 = dfrac{1}{2} cdot 75 = 37dfrac{1}{2} : см^2

Ответ: 37.5 см²

Полученный ответ легко проверить с помощью калькулятора .

Задача 2

Найдите площадь трапеции средняя линия которой равна 18 см, а высота 9 см.

Решение

С решением этой задачи нам поможет вторая формула.

S = m cdot h = 18 cdot 9 = 162 : см^2

Ответ: 162 см²

Воспользуемся калькулятором для проверки результата.

Задача 3

Найдите площадь трапеции диагонали которой равны 10 и 8, а средняя линия равна 3.

Решение

Для решения этой задачи нам поможет третья формула.

На первом этапе вычислим p:

p = dfrac{d_1+d_2+2m}{2} = dfrac{10+8+2 cdot 3}{2} = dfrac{10+8+6}{2} = dfrac{24}{2} = 12

А теперь можно вычислить площадь трапеции:

S = sqrt{p(p-d_1)(p-d_2)(p-2m)} = sqrt{12(12-10)(12-8)(12-2 cdot 3)} = sqrt{12 cdot 2 cdot 4 cdot 6} = sqrt{576} = 24 : см^2

Ответ: 24 см²

Осталось проверить полученный ответ.

Задача 4

Найдите площадь трапеции диагонали которой равны 17 и 15, а средняя линия равна 4.

Решение

Задача похожа на ту, что мы только что решили. Поэтому повторим шаги.

На первом этапе вычислим p:

p = dfrac{d_1+d_2+2m}{2} = dfrac{17+15+ 2 cdot 4}{2} = dfrac{17+15+8}{2} = dfrac{40}{2} = 20

А теперь можно вычислить площадь трапеции:

S = sqrt{p(p-d_1)(p-d_2)(p-2m)} = sqrt{20(20-17)(20-15)(20-2 cdot 4)} = sqrt{20 cdot 3 cdot 5 cdot 12} = sqrt{3600} = 60 : см^2

Ответ: 60 см²

Проверка .

Задача 5

Найдите площадь трапеции диагонали которой равны 8 и 6 а средняя линия равна 5.

Решение

Еще одна типовая задача. Повторим действия как в задачах выше.

На первом этапе вычислим p:

p = dfrac{d_1+d_2+2m}{2} = dfrac{8+6+ 2 cdot 5}{2} = dfrac{8+6+10}{2} = dfrac{24}{2} = 12

А теперь можно вычислить площадь трапеции:

S = sqrt{p(p-d_1)(p-d_2)(p-2m)} = sqrt{12(12-8)(12-6)(12-2 cdot 5)} = sqrt{12 cdot 4 cdot 6 cdot 2} = sqrt{576} = 24 : см^2

Ответ: 24 см²

Проверка .

Задача 6

Найдите площадь равнобедренной трапеции если её основания равны 5 см и 17 см, а боковая сторона равна 10 см.

Решение

Для решения этой задачи используем формулу Брахмагупты.

Сначала вычислим p:

p = dfrac{a+b+2c}{2} = dfrac{5+17+2 cdot 10}{2} = dfrac{22+20}{2} = dfrac{42}{2} = 21

А теперь можно вычислить площадь трапеции:

S = sqrt{(p-a)(p-b)(p-c)^2} = sqrt{(21-5)(21-17)(21-10)^2} = sqrt{16 cdot 4 cdot 11^2} = sqrt{16 cdot 4 cdot 121} = sqrt{7744}= 88 : см^2

Ответ: 88 см²

Проверка .

Задача 7

Острый угол равнобедренной трапеции равен 45°, а основания равны 8 и 6 см. Найдите площадь трапеции.

Решение

Для решения этой задачи воспользуемся формулой.

S = dfrac{1}{2}(b^2-a^2) cdot tg(alpha) = dfrac{1}{2}(8^2-6^2) cdot tg(45°)

Тангенс 45° = 1, продолжим вычисления:

S = dfrac{1}{2}(8^2-6^2) cdot tg(45°) = dfrac{1}{2}(64-36) cdot 1 = dfrac{1}{2} cdot 28 = 14 : см^2

Ответ: 14 см²

Убедиться в правильности решения нам поможет калькулятор .

Источник

Прямоугольная трапеция особенна тем, что имеет сторону, перпендикулярную двум неравным основаниям фигуры. Важным признаком является и наличие двух прямых смежных углов. Поиск площади прямоугольной трапеции возможен по любой из общих формул, предназначенных для данного вычисления любых трапеций (прямоугольной, равнобедренной, произвольной).

5 способов вычисления:

через три стороны трапеции;
умножив высоту трапеции на среднюю линию;
через основание и углы;
через диагонали и углы между ними;
через четыре стороны.

Вычисление площади трапеции через три её стороны (основания и перпендикулярную сторону) подходит только для прямоугольных трапеций.

Площадь прямоугольной трапеции по трём сторонам

Значение высоты прямоугольной трапеции совпадает со значением её стороны, перпендикулярной основаниям фигуры. Площадь такой фигуры можно найти через три известных стороны.

Рисунок 1.

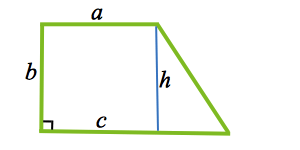
a – малое основание;

b – перпендикулярная сторона;

c – большое основание;

h – высота.

Рисунок 1. Прямоугольная трапеция. Высота h.

[boldsymbol{S}=frac{mathbf{1}}{mathbf{2}} *(boldsymbol{a}+boldsymbol{c}) * boldsymbol{b}, text { где } mathbf{S}], где S – площадь прямоугольной трапеции.

Если половину суммы малого и большого основания умножить на перпендикулярную сторону трапеции или высоту, в результате получается площадь.

Задача.

Найдите площадь прямоугольной трапеции S, если малое основание a составляется 4,84 см, а большое с – 7,88 см, перпендикулярная основаниям высота b равна 4,64 см.

Решение:

Основываясь на данные о трёх её сторонах, по соответствующей формуле найдём площадь.

[boldsymbol{S}=frac{1}{2} *(4,84+7,88) * 4,64=mathbf{2 9}, mathbf{5 1} text { кв.см }]

Ответ: Площадь прямоугольной трапеции равна 29,51 кв.см.

Площадь прямоугольной трапеции по высоте и средней линии

Для расчета площади потребуются данные о высоте трапеции и линии, проведенной посередине фигуры. Произведение этих величин и составит площадь. Рассмотрим рисунок 2.

Рисунок 2.

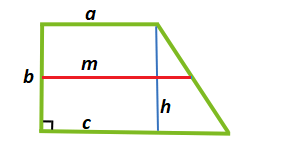
[boldsymbol{S}=boldsymbol{m} * boldsymbol{h}], где S – площадь фигуры, m – средняя линия, а h – высота, которую можно заменять на перпендикулярную основаниям сторонуb.

Задача.

Найдите площадь прямоугольной трапеции S, зная высоту h – 4,64 см и среднюю линию m – 6,36 см.

Решение:

Найдём площадь трапеции путём умножения известных величин.

[boldsymbol{S}=4,64 * 6,36=29,51 text { кв.см }]

Ответ: S = 29,51 кв.см.

Вычисление площади по основаниям и углам

Зная значения оснований трапеции и углов при них, для вычисления площади нужно половину разницы квадратов оснований фигуры умножить на частное из произведения синусов углов при основании и синуса суммы этих углов. Рассмотрим рисунок 3.

Рисунок 3.

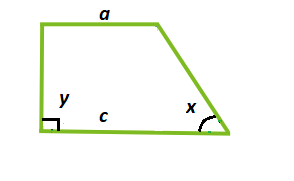
[S=frac{1}{2} *left(c^{2}-a^{2}right) * frac{sin (y) * sin (x)}{sin (y+x)}], где S – площадь; с – большое основание;a – малое основание;

y, x – первый и второй угол при основании.

Задача.

Как узнать площадь прямоугольной трапеции S по формуле оснований и углов, если малое снование a равно 4,84 см, а большое с – 7,88 см, первый угол при основании y прямой, а второй x равен 56,8^о?

Решение:

Рассчитаем площадь трапеции, используя данные об основаниях и углах при большом основании.

[boldsymbol{S}=frac{1}{2} *left(7,88^{2}-4,84^{2}right) * frac{sin (90) * sin (56,8)}{sin (90+56,8)}=mathbf{2 9 , 4 8} mathbf{кв.см}]

Ответ: S = 29.48 кв.см.

Нет времени решать самому?

Наши эксперты помогут!

Площадь прямоугольной трапеции через диагонали и углы между ними

Умножив синус угла, образованный на пересечении диагоналей, на произведение диагоналей, делённое пополам, получим площадь прямоугольной трапеции.

Рисунок 4.

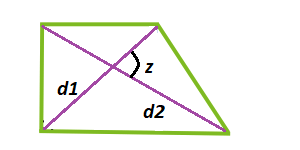
[S=frac{1}{2} * d 1 * d 2 * sin (x)], где S – площадь; d1 – диагональ 1; d2 – диагональ 2; z – угол между диагоналями.

Задача.

Найдите площадь прямоугольной трапеции, имя данные первой диагонали d1, второй – d2 и угла между ними z. d1 = 2,23 см; d2 = 2,65 см, z = 57^o.

Решение:

Пользуясь формулой расчёта площади, при известных диагоналях и углу между ними, составим решение.

[boldsymbol{S}=frac{1}{2} * 2,23 * 2,65 * sin (57)=mathbf{2}, mathbf{4 8} mathbf { кв.см }]

Ответ: S=2,48 кв.см

Площадь прямоугольной трапеции, исходя из значения всех её сторон

Если известны показатели всех сторон прямоугольной трапеции, то вычислить её площадь можно по формуле, приведённой ниже.

[left.S=frac{a+c}{2} * sqrt{e^{2}-left(frac{(c-a)^{2}+e^{2}-b^{2}}{2 *(c-a)}right.}right)^{2}], где a – малое основание; c – большое основание; b – перпендикулярная основаниям сторона; e – неперпендикулярная боковая сторона.

Рисунок 5

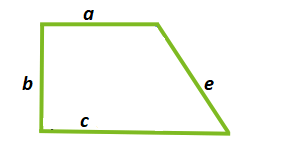
Задача.

Дано: a = 3 см; b = 3 см; c = 5 см; e = 3,5 см.

Найти: площадь трапеции S.

Решение: применяя формулу расчёта площади по всем сторонам фигуры, найдём площадь трапеции.

[S=frac{3+5}{2} * sqrt{3,5^{2}-left(frac{(5-3)^{2}+3,5^{2}-3^{2}}{2 *(5-3)}right)^{2}}=11,98 mathbf { кв.см} .]

Ответ: S = 11,98 кв.см.

Источник

Как найти площадь трапеции? Для этого в зависимости от данных условия можно использовать несколько формул.

1. Площадь трапеции равна произведению полусуммы её оснований на высоту.

Для трапеции ABCD, AD ∥ BC, с высотой BF площадь равна

$[{S_{ABCD}} = frac{{AD + BC}}{2} cdot BF]$

Если AD=a, BC=b, BF=h, формула для нахождения площади трапеции

$[S = frac{{a + b}}{2} cdot h]$

2. Площадь трапеции равна произведению её средней линии на высоту.

$[{S_{ABCD}} = MN cdot BF]$

Если MN=m, BF=h, формула для нахождения площади трапеции через среднюю линию и высоту

3. Площадь трапеции равна половине произведения её диагоналей на синус угла между ними.

$[{S_{ABCD}} = frac{1}{2}AC cdot BD cdot sin angle COD]$

или, так как sin∠BOC=sin(180º-∠COD)=sin∠COD,

$[{S_{ABCD}} = frac{1}{2}AC cdot BD cdot sin angle BOC.]$

Если AC=d1, BD=d2, ∠COD=φ, то формула для нахождения площади трапеции через диагонали —

$[S = frac{1}{2}{d_1} cdot {d_2} cdot sin varphi ]$

Если диагонали трапеции перпендикулярны,

так как sin 90º=1,

то формула площади трапеции

$[S = frac{1}{2}{d_1} cdot {d_2}]$

4. Площадь трапеции равна произведению её полупериметра на радиус вписанной окружности.

Так как в трапецию можно вписать окружность, если суммы ее противолежащих сторон равны, то AB+CD=AD+BC. Следовательно, полупериметр трапеции равен сумме её оснований: p=AD+BC или p=a+b.

Таким образом, получаем еще одну формулу для нахождения площади трапеции через радиус вписанной окружности:

(Так как радиус вписанной в трапецию окружности равен половине высоты трапеции:

$[r = frac{1}{2}h,]$

то эта формула может быть получена непосредственно из формулы из пункта 1).

Источник

Разделы теории

Открыть каталог
Свернуть каталог

Алгебра. Краткий справочник. Формулы

Дроби. Формулы сокращенного умножения

Проценты

Теорема Виета для квадратного и кубического уравнений

Арифметическая прогрессия. Геометрическая прогрессия

Степень. Свойства степеней

Модуль. Корни

Логарифмы. Логарифмические формулы. Свойства логарифмов

Тригонометрические формулы. Таблица углов. Формулы приведения

Тригонометрические формулы. Основное тригонометрическое тождество и следствия

Тригонометрические формулы: синус, косинус, тангенс и котангенс двойного и тройного углов; понижения степени

Тригонометрические формулы суммы и разности углов

Тригонометрические формулы произведения функций

Тригонометрические формулы суммы и разности функций

Тригонометрические формулы вспомогательного аргумента (угла)

Производная. Таблица производных. Связь функции с производной. Касательная. Первообразная

Графики функций. Прямая. Парабола. Функция корня. Тригонометрические функции. Показательная функция. Логарифм

Планиметрия. Краткий справочник. Формулы

Смежные и вертикальные углы. Треугольник. Равнобедренный треугольник. Медиана, биссектриса, высота, средняя линия

Признаки и свойства параллельных прямых. Теорема Фалеса

Параллелограмм. Свойства и признаки

Ромб. Свойства и признаки

Прямоугольник. Квадрат. Свойства и признаки

Трапеция. Равнобедренная трапеция. Средняя линия трапеции

Теорема Пифагора. Пифагоровы тройки

Основные свойства площадей треугольников

Теорема синусов. Теорема косинусов

Центральные углы. Вписанные углы. Угол между хордами. Угол между секущими. Угол между касательной и хордой

Свойства касательных, секущих и хорд окружности. Радикальная ось

Вписанная окружность (описанный треугольник, описанный четырехугольник)

Описанная окружность (вписанный треугольник, вписанный четырехугольник)

Теорема Вариньона. Теорема Менелая. Теорема Чевы. Теорема Ван-Обеля

Теорема Стюарта. Длина биссектрисы и длина медианы треугольника

Площадь выпуклого четырехугольника

Площадь треугольника. Формула Герона

Площадь параллелограмма

Площадь ромба

Площадь прямоугольника. Площадь квадрата.

Площадь трапеции

Площадь правильного треугольника. Площадь квадрата. Площадь правильного шестиугольника

Длина окружности. Длина дуги. Площадь круга. Площадь сектора

Длина отрезка. Середина отрезка. Координаты вектора. Сложение векторов. Скалярное произведение векторов

Стереометрия. Краткий справочник. Формулы

Справочник с основными фактами стереометрии

Теорема о трех перпендикулярах

Призма. Прямая призма. Правильная призма. Объем призмы

Параллелепипед. Прямоугольный параллелепипед. Объем параллелепипеда

Куб. Объем куба. Диагональ куба. Площадь поверхности куба

Пирамида. Прямоугольная пирамида. Правильная пирамида. Объем пирамиды. Тетраэдр

Цилиндр. Объем цилиндра. Площадь поверхности цилиндра

Конус. Объем конуса. Площадь поверхности конуса

Шар. Объем шара. Сфера. Площадь поверхности сферы

Шаровой слой. Шаровой сектор. Шаровой сегмент.

Векторы. Метод координат. Угол между прямыми, плоскостями. Расстояние от точки до плоскости, между скрещивающимися прямыми

Геометрия на плоскости (планиметрия). Часть I. Подробная теория

Введение в планиметрию. Основные факты о треугольниках

Выпуклый четырехугольник

Параллелограмм

Ромб

Прямоугольник и квадрат

Трапеция

Площади многоугольников

Подобие треугольников. Средняя линия треугольника

Треугольник. Важные факты о высоте, биссектрисе и медиане

Длина дуги окружности. Площадь кругового сектора

Геометрия на плоскости (планиметрия). Часть II. Подробная теория

Начальные сведения о синусе, косинусе, тангенсе и котангенсе

Площади многоугольников. Дополнение

Окружность. Основные теоремы

Окружность: описанная около многоугольника

Окружность: вписанная в многоугольник или угол

Теорема синусов и теорема косинусов

Правильный шестиугольник и его свойства

Векторы. Начальные сведения

Векторы на координатной плоскости

Геометрия на плоскости (планиметрия). Часть III. Важные теоремы для решения задания 16

Метод площадей для решения задач

Окружность. Основные теоремы, связанные с окружностями

Подобие треугольников и пропорциональные отрезки

Задачи на теоремы Менелая, Чевы и Стюарта. Формулы для биссектрисы и медианы

Геометрия в пространстве (стереометрия). Подробная теория

Введение в стереометрию. Параллельность

Перпендикулярность. Углы и расстояния в пространстве

Многогранники. Призма. Параллелепипед. Куб

Пирамида

Поверхности вращения: цилиндр, конус, сфера

Построение сечений

Алгебра. Часть I. Подробная теория: рациональные и десятичные дроби, квадратные корни

Рациональные (обыкновенные) дроби и действия с ними. Простые числа

Десятичные дроби и действия с ними

Квадратный корень. Действия с квадратными корнями. Модуль. Сравнение квадратных корней

Алгебра. Часть II. Простейшие уравнения. Задание 5

Линейные, квадратные и простейшие кубические уравнения. Примеры

Простейшие рациональные уравнения. Примеры

Простейшие иррациональные уравнения. Примеры

Простейшие показательные уравнения (с неизвестной в показателе степени). Примеры

Простейшие логарифмические уравнения. Примеры

Алгебра. Часть III. Тригонометрия. Задания 5 и 13

Введение в тригонометрию

Простейшие тригонометрические уравнения (задание 5) и неравенства

Решение простейших тригонометрических уравнений с помощью аркфункций

Тригонометрические формулы. Их вывод

Основные виды тригонометрических уравнений (задание 13)

Алгебра. Часть IV. Показательные и логарифмические уравнения. Смешанные уравнения. Задание 13

Кубические уравнения. Метод деления в столбик. Примеры *

Некоторые известные типы рациональных уравнений *

Алгебра. Часть V. Неравенства. Задание 15

Рациональные неравенства

Показательные неравенства

Логарифмические неравенства

Метод рационализации

Иррациональные неравенства

Алгебра. Часть VI. Взаимосвязь функции и ее производной. Задание 7

Геометрический смысл производной

Связь производной с монотонностью и точками экстремума функции

Физический смысл производной

Первообразная

Алгебра. Часть VII. Исследование функций с помощью производной. Задание 12

Поиск точек экстремума функции

Поиск наибольшего/наименьшего значения функции

Алгебра. Часть IX. Сложные задачи прикладного характера. Задание 17

Банковский кредит. Аннуитетный платеж

Банковский кредит. Дифференцированный платеж

Банковский вклад

Тренировочные варианты ЕГЭ-2018

Вариант № 1 от 11.11.2017

Вариант № 2 от 27.11.2017

Вариант № 3 от 13.01.2018

Вариант № 4 (вторая часть)

Вариант №5 от 06.04.2018

Вариант №6 от 15.04.2018

Пробные ЕГЭ центра “Школково”

Пробный ЕГЭ 03.04.2017

Пробный ЕГЭ 10.04.2017

Тренировочные варианты. Первая часть.

Тренировочный вариант №1

Тренировочный вариант №2

Тренировочный вариант №3

Тренировочный вариант №4

Тренировочный вариант №5

Тренировочный вариант №6

Тренировочные варианты “Школково”. Уровень школьник

Тренировочный вариант №1

Тренировочный вариант №2

Тренировочный вариант №3

Тренировочный вариант №4

Тренировочный вариант №5

Тренировочный вариант №6

Тренировочные варианты “Школково”. Уровень составитель ЕГЭ

Тренировочный вариант №1

Тренировочный вариант №2

Тренировочный вариант №3

Тренировочный вариант №4

Тренировочный вариант №5

Тренировочный вариант №6

Тренировочный вариант №7

Тренировочный вариант №8

Тренировочный вариант №9

Тренировочный вариант №10

Тренировочные варианты “Школково”. Уровень Максим Олегович

Тренировочный вариант №1

Тренировочный вариант №2

Тренировочный вариант №3

Тренировочный вариант №4

Тренировочный вариант №5

Тренировочный вариант №6

Тренировочный вариант №7

ДВИ в МГУ им. М. В. Ломоносова

Вариант 111, июль 2011 года.

Вариант Москва, июль 2014 года.

Вариант Москва, июль 2015 года.

Вариант Ф22, июль 2015 года.

Вариант КМ-15, июль 2015 года.

Вариант Москва, июль 2017 года.

Реальные варианты ЕГЭ 2015

Основная волна

Резервный день. Задания с развернутым ответом

Досрочная волна

Реальные варианты ЕГЭ 2016

Резервный день. Задания с развернутым ответом

Основная волна

Досрочная волна

Реальные варианты ЕГЭ 2017

Досрочная волна. 31 марта 2017

Официальный пробный ЕГЭ. 21 апреля 2017

Досрочная волна. Резерв. 14 апреля 2017

Основная волна. 2 июня 2017. Вторая часть. Вариант 1

Основная волна. 2 июня 2017. Первая и вторая часть. Вариант 2

Основная волна. 2 июня 2017. Первая и вторая часть. Вариант 3

Основная волна. 2 июня 2017. Первая и вторая часть. Вариант 4

Основная волна. 2 июня 2017. Вторая часть. Вариант 5

Резервная волна. 28 июня 2017. Первая и вторая часть. Вариант 1

Резервная волна. 28 июня 2017. Вторая часть. Вариант 2

Реальные варианты ЕГЭ 2018

СтатГрад. Москва. 11 октября 2017

СтатГрад. Москва. 26 января 2018

Досрочная волна. 30 марта 2018

Досрочная волна. Резервный день. 11 апреля 2018

СтатГрад. Москва. 19-23 апреля 2018

Основная волна. Вариант №1. 1 июня 2018

Кликните, чтобы открыть меню

Главная
>
Площадь трапеции

Площадь трапеции

1. Читай полную теорию

2. Вникай в доказательства

3. Применяй на практике

Факт 1.
(bullet) 1. Площадь трапеции равна произведению полусуммы оснований на высоту.
(bullet) 2. Площадь трапеции равна половине произведения диагоналей на синус угла между ними (как площадь любого выпуклого четырехугольника).

Источник

Формулы площади трапеции

Площадь любых трапеций

Площадь равнобедренной трапеции

Определения трапеции

Элементы трапеции

Площадь трапеции

Площадь трапеции через основания и высоту

Площадь трапеции через среднюю линию и высоту

Площадь трапеции через диагонали и среднюю линию

Площадь трапеции через 4 стороны

Площадь трапеции через диагонали и угол между ними

Площадь трапеции через основания и углы при основании

Площадь трапеции через площади треугольников

Площадь трапеции через диагонали и высоту

Площадь трапеции через радиус вписанной окружности и основания

Площадь трапеции через перпендикулярные диагонали

Площадь равнобедренной (равнобокой) трапеции

Площадь равнобедренной трапеции через основания и высоту

Площадь равнобедренной трапеции через 3 стороны (формула Брахмагупты)

Площадь равнобедренной трапеции через верхнее основание, боковую сторону и угол при нижнем основании

Площадь равнобедренной трапеции через нижнее основание, боковую сторону и угол при нижнем основании

Площадь равнобедренной трапеции через основания и угол

Площадь равнобедренной трапеции через диагонали и угол между ними

Площадь равнобедренной трапеции через боковую сторону, угол при основании и среднюю линию

Площадь равнобедренной трапеции через радиус вписанной окружности и угол при основании

Площадь равнобедренной (равнобокой) трапеции, в которую можно вписать окружность

Площадь равнобедренной трапеции, в которую можно вписать окружность, через высоту (диаметр вписанной окружности) и угол при основании

Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и угол при основании

Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и радиус вписанной окружности

Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания

Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и боковую сторону

Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и среднюю линию

Примеры задач на нахождение площади трапеции

Площадь прямоугольной трапеции по трём сторонам

Площадь прямоугольной трапеции по высоте и средней линии

Вычисление площади по основаниям и углам

Площадь прямоугольной трапеции через диагонали и углы между ними

Площадь прямоугольной трапеции, исходя из значения всех её сторон

Площадь трапеции

Вам также может понравиться

Как найти абонента на карте бесплатно

Как найти чат музыка

Как найти свое резюме на фарпосте

Добавить комментарий Отменить ответ