Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
2
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
3
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
4
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
5
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Пройти тестирование по этим заданиям
18. Площади геометрических фигур
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Площадь трапеции
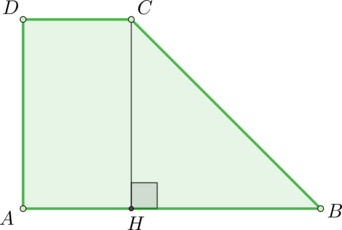
Найдите площадь прямоугольной трапеции, основания которой равны (6) и (2), большая боковая сторона составляет с основанием угол (45^circ).
Проведем высоту (CH).
Так как (angle HBC=45^circ), то (angle HCB=45^circ). Следовательно, (triangle HBC) равнобедренный и (HB=HC).
(ADCH) – прямоугольник, следовательно, (AH=DC=2). Тогда (CH=HB=6-2=4). Тогда площадь трапеции равна [S=dfrac{AB+DC}2cdot CH=dfrac{2+6}2cdot 4=16]
Ответ: 16
Основания прямоугольной трапеции равны (12) и (4). Ее площадь равна (64). Найдите острый угол этой трапеции. Ответ дайте в градусах.
Проведем высоту (CH).
(ADCH) – прямоугольник, следовательно, (AH=DC=4). Тогда (HB=12-4=8). Площадь трапеции равна [64=dfrac{AB+DC}2cdot CH=dfrac{4+12}2cdot CHquadRightarrowquad
CH=8] Заметим, что мы получили, что (CH=HB=8). То есть (triangle
CHB) равнобедренный, значит, углы при основании равны, то есть (angle HCB=angle HBC). Так как сумма острых углов в прямоугольном треугольнике равна (90^circ), то (angle B=angle
HBC=90^circ:2=45^circ).
Ответ: 45
Основания трапеции равны (18) и (6), боковая сторона, равная (7), образует с одним из оснований угол (150^circ). Найдите площадь трапеции.
Пусть (AD=7), тогда (angle ADC=150^circ). По свойству трапеции (angle DAB=180^circ-150^circ=30^circ). Проведем (DHperp
AB).
Рассмотрим (triangle ADH). Катет, лежащий против угла (30^circ), равен половине гипотенузы, следовательно, (DH=AD:2=3,5). Тогда площадь трапеции равна [S=dfrac{AB+DC}2cdot DH=dfrac{18+6}2cdot 3,5=42]
Ответ: 42
Основания трапеции равны (27) и (9), боковая сторона равна (8). Площадь трапеции равна (72). Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ дайте в градусах.
Пусть (AD=8). Проведем (DHperp AB).
Тогда площадь трапеции равна [72=dfrac{AB+DC}2cdot DH=dfrac{27+9}2cdot DHquadRightarrowquad
DH=4] Рассмотрим прямоугольный (triangle ADH). Так как катет (DH) равен половине гипотенузы (AD), то угол (DAH) равен (30^circ).
Ответ: 30
Основания равнобедренной трапеции равны (14) и (26), а ее боковые стороны равны (10). Найдите площадь трапеции.
Проведем высоту (BH). По свойству равнобедренной трапеции (AH=(AD-BC):2=(26-14):2=6).
Тогда из прямоугольного треугольника (ABH): [BH=sqrt{AB^2-AH^2}=sqrt{10^2-6^2}=8] Тогда площадь трапеции: [S=dfrac{AD+BC}2cdot BH=dfrac{26+14}2cdot 8=160]
Ответ: 160
Основания равнобедренной трапеции равны (7) и (13), а ее площадь равна (40). Найдите боковую сторону трапеции.
Проведем высоту (BH).
Площадь трапеции равна [40=dfrac{AD+BC}2cdot BH=dfrac{7+13}2cdot BHquadRightarrowquad BH=
4] Рассмотрим прямоугольный (triangle ABH). По свойству равнобедренной трапеции (AH=(AD-BC):2=(13-7):2=3). Следовательно, [AB=sqrt{AH^2+BH^2}=5]
Ответ: 5
Основания равнобедренной трапеции равны (14) и (26), а ее периметр равен (60). Найдите площадь трапеции.
Проведем высоту (BH). По свойству равнобедренной трапеции (AH=(AD-BC):2=(26-14):2=6).
Так как периметр трапеции равен (60), а боковые стороны равны, то [AB=dfrac{60-14-26}2=10] Тогда из прямоугольного треугольника (ABH): [BH=sqrt{AB^2-AH^2}=sqrt{10^2-6^2}=8] Тогда площадь трапеции: [S=dfrac{AD+BC}2cdot BH=dfrac{26+14}2cdot 8=160]
Ответ: 160

УСТАЛ? Просто отдохни
Задание 972
Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции.
Ответ: 30
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Площадь трапеции вычисляется по формуле $$S=frac{a+b}{2}*h$$. Получаем $$40=frac{7+13}{2}*CH$$. Отсюда CH = 4.
Из треугольника CHD по теореме Пифагора находим CD = 5. Отсюда периметр равен 7 + 13 + 5 + 5 = 30
Задание 1858
Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 30° и 45° соответственно.
Ответ: 105
Скрыть
$$angle A=angle BAC+angle CAD=30+45=75^{circ}$$, тогда по свойству углов трапеции: $$angle B=180-angle A=105^{circ}$$
Задание 1859
Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 50° соответственно.
Ответ: 80
Скрыть
$$angle A=angle BAC+angle CAD=30+50=80^{circ}$$
Задание 1860
Сумма двух углов равнобедренной трапеции равна 140°. Найдите больший угол трапеции. Ответ дайте в градусах.
Ответ: 110
Скрыть
Так как дана равнобедренная трапеция, то сумма острых углов при большем основании будет составлять 140 градусов, $$angle A=angle B=frac{140}{2}=70^{circ}$$, по свойству углов трапеции: $$angle D=180-angle A=110^{circ}$$
Задание 1861
Найдите меньший угол равнобедренной трапеции, если два ее угла относятся как 1:2. Ответ дайте в градусах.
Ответ: 60
Скрыть
Пусть меньший угол равен х, тогда больший угол равен 2х. По свойству углов трапеции получаем, что $$x+2x=180Leftrightarrow$$$$x=60$$, то есть меньший угол составляет $$60^{circ}$$
Задание 1863
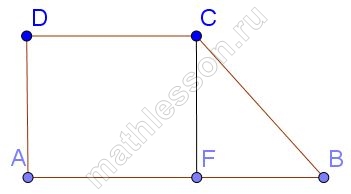
Тангенс острого угла прямоугольной трапеции равен $$frac{5}{6}$$. Найдите её большее основание, если меньшее основание равно высоте и равно 15.
Ответ: 33
Скрыть
Опустим высоту CF, тогда из прямоугольного треугольника CFB: $$FB=frac{CF}{tgB}=frac{15}{frac{5}{6}}=18$$. DC=AF=15, тогда AB=15+18=33.
Задание 1864
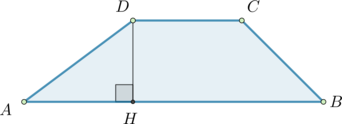
В равнобедренной трапеции известны высота 4, меньшее основание 8 и угол при основании $$45^{circ}$$. Найдите большее основание.
Ответ: 16
Скрыть
Опустим высоты DE=CF=4, тогда из прямоугольного треугольника ADE: так как $$angle A=45^{circ}$$, то $$angle ADE=90-45=45^{circ}$$, следовательно, реугольник AED – равнобедренный, и AE=DE=4, аналогично FB=4. Но EF=DC=8, тогда AB=4+4+8=16.
Задание 1865
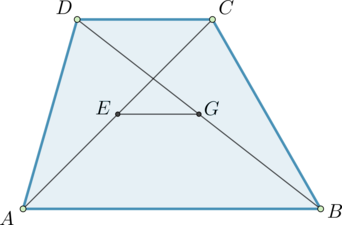
Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
Ответ: 5
Скрыть
EG – средняя линия треугольника ADB, тогда $$EG=frac{1}{2}=AB=5$$, аналогично GF – средняя линия треугольника DCB, тогда $$GF=frac{1}{2}DC=2$$, наибольший в таком случае равен 5
Примечение: больший из отрезков всегда будет равен половине большего основания
Задание 1866
Основания равнобедренной трапеции равны 50 и 104, боковая сторона 45. Найдите длину диагонали трапеции.
Ответ: 85
Скрыть
Опустим две высоты DE=CF, тогда AE=FB (из равенства прямоугольных треугольников ADE и CFB по катету и гипотенузе), и DC=EF=50, тогда $$AE=FB=frac{104-50}{2}=27$$. Тогда из прямоугольного треугольника ADE : $$DE=sqrt{AD^{2}-AE^{2}}=sqrt{45^{2}-27^{2}}=36$$, следовательно, EB=AB-AE=104-27=77. Тогда из прямоугольного треугольника DEB: $$DB=sqrt{DE^{2}+EB^{2}}=sqrt{77^{2}+36^{2}}=85$$
Задание 1867
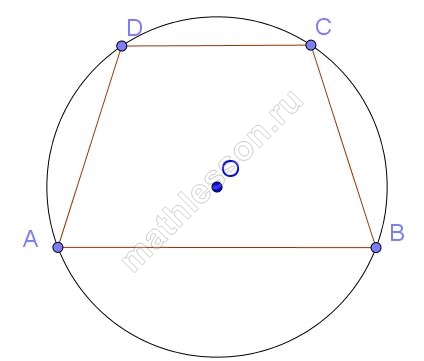
Около трапеции, один из углов которой равен 49°, описана окружность. Найдите остальные углы трапеции.
Запишите величины углов в ответ через точку с запятой в порядке неубывания.
Ответ: 49; 131; 131
Скрыть
По свойству вписанного четырехугольник $$angle A+angle C=180^{circ}$$, пусть $$angle A=49^{circ}Rightarrow$$$$angle C=180-49=131^{circ}$$. По свойству углов трапеции $$angle B=180-angle C=180-131=49^{circ}$$, аналогично $$angle D=180-angle A=131^{circ}$$
Задание 1868
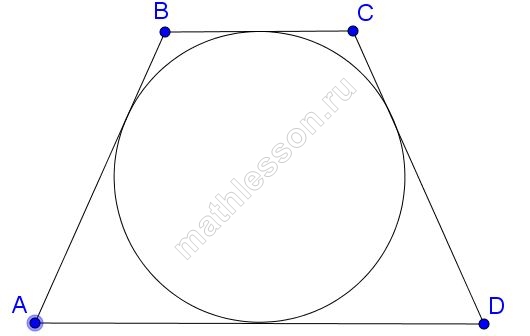
В трапецию, сумма длин боковых сторон которой равна 24, вписана окружность. Найдите длину средней линии трапеции.
Ответ: 12
Скрыть
По свойству описанного четырехугольника AD+BC=AB+CD, тогда сумма оснований тоже 24, средняя линия же равна полусумме оснований, то есть 24/2=12.
Задание 1965
Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а синус угла между ней и одним из оснований равен $$frac{1}{3}$$. Найдите площадь трапеции.
Ответ: 30
Скрыть
- Опустим высоту CE. Пусть $$sin D=frac{1}{3}$$, тогда из прямоугольного треугольника CED: $$CE=CD*sin D=2$$
- Из формулы площади трапеции: $$S_{ABCD}=frac{18+12}{2}*2=30$$
Задание 1966
Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а косинус угла между ней и одним из оснований равен $$frac{2sqrt{2}}{3}$$. Найдите площадь трапеции.
Ответ: 30
Скрыть
- Пусть $$cos D =frac{2sqrt{2}}{3}$$, опустим высоту CE. Тогда из треугольника CED: $$ED=CD*cos D=6*frac{2sqrt{2}}{3}=4sqrt{2}$$
- По теореме Пифагора из треугольника CED: $$CE=sqrt{6^{2}-(4sqrt{2})^{2}}=2$$
- Из формулы площади трапеции $$S_{ABCD}=frac{18+12}{2}*2=30$$
Задание 1967
Средняя линия трапеции равна 11, а меньше основание равно 5. Найдите большее основание трапеции.
Ответ: 17
Скрыть
Пусть a – большее основание, тогда из формулы длины средней линии трапеции : $$a=2*11-5=17$$
Задание 1968
Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
Ответ: 15
Скрыть
- Пусть $$angle D=30^{circ}$$. Опустим высоту CE, тогда из прямоугольного треугольника CED: $$CE=CD*sin D=2,5$$
- По формуле площади трапеции $$S_{ABCD}=frac{3+9}{2}*2,5=15$$
25
Июл 2013
Категория: 01 Геометрия
01. Трапеция
2013-07-25
2022-09-11
Задача 1. Основания равнобедренной трапеции равны и
Боковые стороны равны
Найдите синус острого угла трапеции.
Решение: + показать
Задача 2. Большее основание равнобедренной трапеции равно Боковая сторона равна
Синус острого угла равен
Найдите меньшее основание.
Решение: + показать
Задача 3. Основания равнобедренной трапеции равны и
Тангенс острого угла равен
. Найдите высоту трапеции.
Решение: + показать
Задача 4. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна ? Ответ дайте в градусах.
Решение: + показать
Задача 5. Найдите среднюю линию трапеции, если ее основания равны и
Решение: + показать
Задача 6. Средняя линия трапеции равна а меньшее основание равно
Найдите большее основание трапеции.
Решение: + показать
Задача 7. Основания трапеции равны и
Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.
Решение: + показать
Задача 8. Основания трапеции равны и
Найдите отрезок, соединяющий середины диагоналей трапеции.
Решение: + показать
Задача 9. В равнобедренной трапеции основания равны и
острый угол равен
. Найдите ее периметр.
Решение: + показать
Задача 10. Основания трапеции равны и
боковая сторона равна
Площадь трапеции равна
Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ дайте в градусах.
Решение: + показать
Задача 11. Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного отсекает треугольник, периметр которого равен
Найдите периметр трапеции.
Решение: + показать
Задача 12. Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины и
Найдите среднюю линию этой трапеции.
Решение: + показать
Задача 13. Основания трапеции относятся как а средняя линия равна
Найдите меньшее основание.
Решение: + показать
Задача 14. В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна Найдите ее среднюю линию.
Решение: + показать
Задача 15. Найдите площадь прямоугольной трапеции, основания которой равны и
большая боковая сторона составляет с основанием угол
Решение: + показать
Задача 16. Основания равнобедренной трапеции равны и
а ее периметр равен
Найдите площадь трапеции.
Решение: + показать
Задача 17. Найдите среднюю линию трапеции , если стороны квадратных клеток равны
.
Решение: + показать

Автор: egeMax |
комментариев 14
Печать страницы
- Найдите площадь трапеции, вершины которой имеют координаты (1;1), (2;4), (10;4), (3;1).
2. На клетчатой бумаге размером 1х1 изображен треугольник. Найдите его площадь.
3. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равен 5. Найдите площадь заштрихованной фигуры.
4. На клетчатой бумаге изображен треугольник. Найдите его площадь
5. Найдите площадь трапеции, изображенной на рисунке.
7.План местности разбит на клетки. Каждая клетка обозначает квадрат 1м × 1м. Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах