Как найти площадь трапеции изображенной на рисунке - Сайт, где вы сможете решить свои вопросы

Каталог заданий.
Трапеция

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Тип 17 № 39

Найдите площадь трапеции, изображённой на рисунке.

Аналоги к заданию № 39: 117 143 311682 … Все

Источник: Демонстрационная версия ГИА—2013 по математике

Решение

Помощь

Тип 17 № 117

Найдите площадь трапеции, изображённой на рисунке.

Аналоги к заданию № 39: 117 143 311682 … Все

Источник: ГИА по математике 28.05.2013. Основная волна. Вариант 1309

Решение

Помощь

Тип 17 № 143

Найдите площадь трапеции, изображённой на рисунке.

Аналоги к заданию № 39: 117 143 311682 … Все

Источник: ГИА по математике 28.05.2013. Основная волна. Вариант 1313

Решение

Помощь

Тип 17 № 169881

Основания трапеции равны 18 и 12, одна из боковых сторон равна а угол между ней и одним из оснований равен 135°. Найдите площадь трапеции.

Аналоги к заданию № 169881: 339837 169882 348664 … Все

Решение

Помощь

Тип 17 № 169883

Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а синус угла между ней и одним из оснований равен Найдите площадь трапеции.

Аналоги к заданию № 169883: 169884 169885 324155 … Все

Решение

Помощь

Пройти тестирование по этим заданиям

Источник

Рассмотрим несколько задач.

Задача #1

(Номер задачи на fipi.ru — B11571). На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Прежде чем приступать к решению задачи, вспомним теорию >>

Трапеция — четырёхугольник, две стороны которой параллелльны, а две другие нет. Параллельные стороны называются основаниями, а непаралельные — боковыми.

Площадь трапеции вычисляется по формуле:

$[S=frac{a+b}{2}cdot h]$

где a и b — основания трапеции, h — высота трапеции.

Решение:
Посмотрим на рисунок. Из него видно, что основания трапеции равны соответственно: a = 2, b = 6. Из рисунка также находим высоту трапеции: h = 7.

Таким образом, осталось подставить все найденный значения в формулу и найти площадь трапеции:

$[S=frac{2+6}{2}cdot 7 = 28]$

Ответ: площадь трапеции равна: 28 ед. кв.

Задача #2

(Номер задачи на fipi.ru — E46263). На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Решение:
Посмотрим на рисунок. Из него видно, что основания трапеции равны соответственно: a = 4, b = 8. Из рисунка также находим высоту трапеции: h = 6.

Таким образом, осталось подставить все найденный значения в формулу и найти площадь трапеции:

$[S=frac{4+8}{2}cdot 6 = 36]$

Ответ: площадь трапеции равна: 36 ед. кв.

Задача #3

(Номер задачи на fipi.ru — 283DE4). На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Решение:
Посмотрим на рисунок. Из него видно, что основания трапеции равны соответственно: a = 2, b = 6. Из рисунка также находим высоту трапеции: h = 3.

Таким образом, осталось подставить все найденный значения в формулу и найти площадь трапеции:

$[S=frac{2+6}{2}cdot 3 = 12]$

Ответ: площадь трапеции равна: 12 ед. кв.

Задача #4

(Номер задачи на fipi.ru — 383C46). На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Решение:
Посмотрим на рисунок. Из него видно, что основания трапеции равны соответственно: a = 3, b = 7. Из рисунка также находим высоту трапеции: h = 2.

Таким образом, осталось подставить все найденный значения в формулу и найти площадь трапеции:

$[S=frac{3+7}{2}cdot 2 = 10]$

Ответ: площадь трапеции равна: 10 ед. кв.

Задача #5

(Номер задачи на fipi.ru — 2E7B84). На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Решение:
Посмотрим на рисунок. Из него видно, что основания трапеции равны соответственно: a = 3, b = 7. Из рисунка также находим высоту трапеции: h = 6.

Таким образом, осталось подставить все найденный значения в формулу и найти площадь трапеции:

$[S=frac{3+7}{2}cdot 6 = 30]$

Ответ: площадь трапеции равна: 30 ед. кв.

Источник

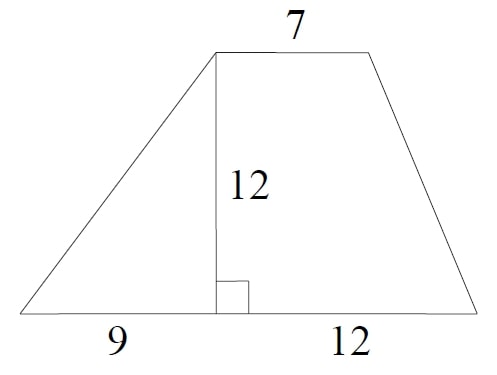
Найдите площадь трапеции, изображённой на рисунке.

Решение:

Площадь трапеции находится по формуле:

S=frac{a+b}{2}cdot h

a = 7
b = 9 + 12 = 21
h = 12

S=frac{7+21}{2}cdot 12=frac{28}{2}cdot 12=14cdot 12=168

Ответ: 168.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 4.3 / 5. Количество оценок: 18

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Источник

Площадь трапеции

Трапецией называется четырехугольник, у
которого только две противолежащие стороны параллельны. Они называются основаниями,
две другие – боковыми.

I. Площадь трапеции равна произведению
полусуммы ее оснований на высоту: