Как найти площадь трапеции изображенном на графике - Сайт, где вы сможете решить свои вопросы

Определенный интеграл. Площадь криволинейной трапеции

Теорема о площади криволинейной трапеции
Формула Ньютона-Лейбница
Геометрический смысл теоремы Лагранжа о среднем
Площадь плоской фигуры, ограниченной двумя кривыми
Примеры

п.1. Теорема о площади криволинейной трапеции

Фигуру, ограниченную прямыми (x=a, x=b), осью абсцисс (y=0) и графиком функции (y=f(x)) называют криволинейной трапецией.

Теорема
Площадь криволинейной трапеции, образованной графиком функции (y=f(x)) на интервале [a;b], равна (F(b)-F(a)), где (F(x)) – первообразная функции (f(x)) на [a;b].

Доказательство:
Выберем на интервале (xin [a;b]). Площадь соответствующей криволинейной трапеции (S(x)) является функцией от (x). Дадим переменной (x) приращение (triangle x).
Площадь криволинейной трапеции на интервале (left[a;x+triangle xright]) равна сумме
(S(x+triangle x)=S(x)+S(triangle x)). Откуда приращение площади: $$ triangle S=S(triangle x)=S(x+triangle x)-S(x) $$ По теореме о среднем (см. ниже в этом параграфе) между (x) и (x+triangle x) всегда найдется такое (t), что приращение площади равно произведению: $$ triangle S=f(t)cdot (x+triangle x-x)=f(t)cdot triangle x $$ Если (triangle xrightarrow 0), то (trightarrow x), и в пределе получаем: begin{gather*} S'(x)=lim_{triangle xrightarrow 0}frac{triangle S}{triangle x}=lim_{triangle xrightarrow 0} frac{f(t)cdot triangle x}{triangle x}=lim_{triangle xrightarrow 0}f(t)=f(x) end{gather*} Т.е. (S(x)) является первообразной для (f(x)) на [a;b]. В общем виде: $$ S(x)=F(x)+C $$ Найдем C. В точке a: $$ S(a)=0=F(a)+CRightarrow C=-F(a) $$ Тогда вся площадь: $$ S=S(b)=F(b)+C=F(b)-F(a) $$ Что и требовалось доказать.

п.2. Формула Ньютона-Лейбница

Площадь криволинейной трапеции, образованной графиком функции (y=f(x)) на интервале [a;b] записывают в виде определенного интеграла: $$ S=int_{a}^{b}f(x)dx $$ По формуле Ньютона-Лейбница определенный интеграл равен: $$ int_{a}^{b}f(x)dx=F(x)|_a^b=F(a)-F(b) $$

Например:
Найдем площадь фигуры, ограниченной осью абсцисс и графиком функции $$ y=3-2x-x^2 $$

Построим график
(см. §28 справочника для 8 класса).
Это парабола. (alt 0) – ветки вниз.
Координаты вершины: begin{gather*} x_0=-frac{b}{2a}=-frac{-2}{2cdot (-1)}=-1,\ y_0=3+2-1=4 end{gather*} Точки пересечения с осью OX: begin{gather*} 3-2x-x^2=0Rightarrow x^2+2x-3=0\ (x+3)(x-1)=0Rightarrow left[ begin{array}{l} x=-3,\ x=1 end{array} right. end{gather*} Точка пересечения с осью OY: $$ x=0, y=3 $$

Необходимо найти площадь заштрихованной фигуры.
Функция: (f(x)=3-2x-x^2)
Пределы интегрирования: (a=-3, b=1) begin{gather*} S=int_{-3}^{1}(3-2x-x^2)dx=left(3x-2cdotfrac{x^2}{2}-frac{x^3}{3}right)|_{1}^{-3}=left(3x-x^2-frac{x^3}{3}right)|_{1}^{-3}=\ =left(3-cdot 1-1^2-frac{1^3}{3}right)-left(3cdot(-3)-(-3)^2-frac{(-3)^3}{3}right)=2-frac13+9=10frac23 end{gather*} Ответ: (10frac23)

п.3. Геометрический смысл теоремы Лагранжа о среднем

Теорема Лагранжа о среднем
Если функция (F(x)) непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b), то существует такая точка (muin(a;b)), что $$ F(b)-F(a)=F'(mu)(a-b) $$ Пусть (F'(x)=f(x)), т.е. функция (F(x)) является первообразной для (f(x)). Тогда: $$ F(b)-F(a)=int_{a}^{b}f(x)dx=f(mu)(b-a) $$

Геометрический смысл теоремы Лагранжа о среднем в интегральной форме заключается в том, что площадь криволинейной трапеции равна площади прямоугольника с основанием (d=b-a) и высотой (h=f(mu)), где (aleqmuleq b).
Теорема о среднем используется при доказательстве многих формул, связанных с использованием определенных интегралов (центра тяжести тела, площади поверхности и т.д.).

п.4. Площадь плоской фигуры, ограниченной двумя кривыми

Площадь плоской фигуры, ограниченной прямыми (x=a, x=b, alt b) и кривыми (y=f(x), y=g(x)), причем (f(x)geq g(x)) для любого (xin [a;b]), равна: $$ S=int_{a}^{b}(f(x)-g(x))dx $$

Например:
Найдем площадь фигуры, ограниченной двумя параболами (y=x^2) и (y=4x-x^2).

Найдем точки пересечения парабол: $$ x^2=4x-x^2Rightarrow 2x^2-4x=0Rightarrow 2x(x-2)=0Rightarrow left[ begin{array}{l} x=0\ x=2 end{array} right. $$ Строим графики.

Необходимо найти площадь заштрихованной фигуры.
Функция сверху: (f(x)=4x-x^2)
Функция снизу: (g(x)=x^2)
Пределы интегрирования: (a=0, b=2) begin{gather*} S=int_{0}^{2}left((4x-x^2)-x^2right)dx=int_{0}^{2}(4x-2x^2)dx=left(4cdotfrac{x^2}{2}-2cdotfrac{x^3}{3}right)|_0^2=\ =left(2x^2-frac23 x^3right)|_0^2=2cdot 2^2-frac23cdot 2^3-0=8-frac{16}{3}=frac83=2frac23 end{gather*} Ответ: (2frac23)

п.5. Примеры

Пример 1. Найдите определенный интеграл:
a) (int_{-2}^{3}x^2dx) $$ int_{-2}^{3}x^2dx=frac{x^3}{3}|_{-2}^{3}=frac{3^3}{3}-frac{(-2)^3}{3}=9-frac83=frac{19}{3}=6frac13 $$
б) (int_{0}^{fracpi 3}sinxdx) $$ int_{0}^{fracpi 3}sinxdx=(-cosx)|_{0}^{fracpi 3}=-cosfracpi 3+cos0=-frac12+1=frac12 $$
в) (int_{1}^{2}left(e^x+frac 1xright)dx) $$ int_{1}^{2}left(e^x+frac 1xright)dx=(e^x+ln|x|)|_{1}^{2}=e^2+ln 2-e^1-underbrace{ln 1}_{=0}=e(e-1)+ln 2 $$
г) (int_{2}^{3}(2x-1)^2 dx) begin{gather*} int_{2}^{3}(2x-1)^2 dx=frac12cdotfrac{(2x-3)^3}{3}|_{2}^{3}=frac16((2cdot 3-1)^3)-(2cdot 2-1)^3)=frac{5^3-3^3}{6}=\ =frac{125-27}{6}=frac{98}{6}=frac{49}{3}=16frac13 end{gather*}
д) (int_{1}^{3}frac{dx}{3x-2}) begin{gather*} int_{1}^{3}frac{dx}{3x-2}=frac13cdot ln|3x-2| |_{1}^{3}=frac13left(ln 7-underbrace{ln 1}_{=0}right)=frac{ln 7}{3} end{gather*}
e) (int_{-1}^{4}frac{dx}{sqrt{3x+4}}) begin{gather*} int_{-1}^{4}frac{dx}{sqrt{3x+4}}=frac13cdotfrac{(3x+4)^{-frac12+1}}{-frac12+1}|_{-1}^{4}=frac23sqrt{3x+4}|_{-1}^{4}=\ =frac23left(sqrt{3cdot 4+4}-sqrt{3cdot(-1)+4}right)=frac23(4-1)=2 end{gather*}

Пример 2. Найдите площадь фигуры под кривой на заданном интервале:
a) (f(x)=x^3+3, xinleft[-1;1right])
$$ S=int_{-1}^{1}(x^3+3)dx=left(frac{x^4}{4}+3xright)|_{-1}^{1}=frac14+3-left(frac14-3right)=6 $$
б) (f(x)=sin2x, xinleft[0;fracpi 2right])
$$ S=int_{0}^{fracpi 2}sin2xdx=-frac12cos2x|_{0}^{fracpi 2}=-frac12left(cosleft(2cdotfracpi 2right)-cos0right)=-frac12(-1-1)=1 $$
в) (f(x)=frac4x+3, xinleft[2;6right])

(f(x)=frac4x+3) – гипербола с асимптотами (x=0, y=3)
Площадь под кривой: begin{gather*} S=int_{2}^{6}left(frac4x+3right)dx=(4cdot ln|x|+3x)|_{2}^{6}=(4ln 6+18)-(4ln 2+6)=\ =4(ln 6-ln 2)+12=4lnfrac62+12=4ln 3+12=4(ln 3+3) end{gather*}
г) (f(x)=frac{1}{sqrt{x}}, xinleft[1;4right])
$$ S=int_{1}^{4}frac{dx}{sqrt{x}}=frac{x^{-frac12+1}}{-frac12+1}|_{1}^{4}=2sqrt{x}|_{1}^{4}=2(sqrt{4}-sqrt{1})=2 $$

Пример 3. Найдите площадь фигуры, ограниченной линиями:
a) (y=x-2, y=x^2-4x+2)
Найдем точки пересечения прямой и параболы: $$ x-2=x^2-4x+2Rightarrow x^2-5x+4=0Rightarrow (x-1)(x-4)=0Rightarrow left[ begin{array}{l} x=1,\ x=4 end{array} right. $$
Функция сверху: (f(x)=x-2)
Функция снизу: (g(x)=x^2-4x+2)
Пределы интегрирования: (a=1, b=4) begin{gather*} S=int_{1}^{4}left((x-2)-(x^2-4x+2)right)dx=int_{1}^{4}(-x^2+5x-4)dx=\ =left(-frac{x^3}{3}+frac{5x^2}{2}-4xright)|_{1}^{4}=left(-frac{64}{3}+5cdotfrac{16}{2}-4cdot 4right)-left(-frac13+frac52-4right)=\ =-frac{63}{3}+24+1,5=4,5 end{gather*} Ответ: 4,5
б) (y=e^{frac x2}, y=frac1x, x=2, x=3)

Функция сверху: (f(x)=e^{x/2})
Функция снизу: (g(x)=frac1x)
Пределы интегрирования: (a=2, b=3) begin{gather*} S=int_{2}^{3}left(e^{x/2}-frac1xright)dx=(2e^{x/2}-ln|x|)|_{2}^{3}=left(2e^{frac32}-ln 3right)-(2e-ln 2)=\ =2e^{frac32}-2e-ln 3+ln 2=2e(sqrt{e}-1)+lnfrac23 end{gather*} Ответ: (2e(sqrt{e}-1)+lnfrac23)
в*) (y=3-x^2, y=1+|x|)
Найдем точки пересечения ломаной и параболы: begin{gather*} 3-x^2=1+|x|Rightarrow x^2+|x|-2=0Rightarrow left[ begin{array}{l} begin{cases} xgeq 0\ x^2+x-2=0 end{cases} \ begin{cases} xlt 0\ x^2-x-2=0 end{cases} end{array} right. Rightarrow left[ begin{array}{l} begin{cases} xgeq 0\ (x+2)(x-1)=0 end{cases} \ begin{cases} xlt 0\ (x-2)(x+1)=0 end{cases} end{array} right. Rightarrow \ left[ begin{array}{l} begin{cases} xgeq 0\ left[ begin{array}{l} x=-2\ x=1 end{array} right. end{cases} \ begin{cases} xlt 0\ left[ begin{array}{l} x=2\ x=-1 end{array} right. end{cases} end{array} right. Rightarrow left[ begin{array}{l} x=1\ x=-1 end{array} right. end{gather*}
Функция сверху: (f(x)=3-x^2)
Функция снизу: (g(x)=1+|x|)
Пределы интегрирования: (a=-1, b=1)
Чтобы не раскрывать модуль под интегралом, заметим, что площади на интервалах [-1;0] и [0;1] равны, т.к. обе функции четные и симметричные относительно оси OY. Поэтому можно рассматривать только положительные (xinleft[0;1right]), найти для них интеграл (площадь) и умножить на 2: begin{gather*} S=2int_{0}^{1}left((3-x^2)-(1+x)right)dx=2int_{0}^{1}(-x^2-x+2)dx=2left(-frac{x^3}{3}-frac{x^2}{2}+2xright)|_{0}^{1}=\ =2left(-frac13-frac12+2right)-0=frac73=2frac13 end{gather*} Ответ: (2frac13)
г*) (y=3sinx, y=cosx, x=-frac{5pi}{4}, x=fracpi 4)

На отрезке (left[-frac{5pi}{4};-frac{3pi}{4}right]) синус над косинусом, далее на (left[-frac{3pi}{4};frac{pi}{4}right]) – косинус над синусом.
Площадь фигуры, закрашенной голубым, в два раза больше площади фигуры, закрашенной сиреневым. Поэтому общая площадь будет равна трем площадям, закрашенным сиреневым: begin{gather*} S=3int_{-frac{5pi}{4}}^{-frac{3pi}{4}}(sinx-cosx)dx=3(-cosx-sinx)|_{-frac{5pi}{4}}^{-frac{3pi}{4}}=-3(cosx+sinx)|_{-frac{5pi}{4}}^{-frac{3pi}{4}} end{gather*} Прибавим полный период, он одинаков для обеих функций:
(-frac{3pi}{4}+2pi=frac{5pi}{4}; -frac{5pi}{4}+2pi=frac{3pi}{4}) begin{gather*} -3(cosx+sinx)|_{-frac{5pi}{4}}^{-frac{3pi}{4}}=-3left(cosleft(frac{5pi}{4}right)+sinleft(frac{5pi}{4}right)-cosleft(frac{3pi}{4}right)-sinleft(frac{3pi}{4}right)right)=\ =-3left(-frac{sqrt{2}}{2}-frac{sqrt{2}}{2}+frac{sqrt{2}}{2}-frac{sqrt{2}}{2}right)=3sqrt{2} end{gather*} Ответ: (3sqrt{2})

Пример 4*. Пусть (S(k)) – это площадь фигуры, образованной параболой (y=x^2+2x-3) и прямой (y=kx+1). Найдите (S(-1)) и вычислите наименьшее значение (S(k)).

1) Найдем (S(-1)).
(k=-1, y=-x+1 )

Точки пересечения прямой и параболы: begin{gather*} -x+1=x^2+2x-3\ x^2+3x-4=0\ (x+4)(x-1)=0Rightarrow left[ begin{array}{l} x=-4,\ x=1 end{array} right. end{gather*} Функция сверху: (y=-x+1)
Функция снизу: (y=x^2+2x-3)
Пределы интегрирования: (a=-4, b=1)

begin{gather*} S(-1)=int_{-4}^{1}left((-x+1)-(x^2+2x-3)right)dx=int_{-4}^{1}(-x-3x+4)dx=\ =left(-frac{x^3}{3}-frac{3x^2}{2}+4xright)|_{-4}^{1}=left(-frac13-frac32+4right)-left(frac{64}{3}-24-16right)=-21frac23+42frac12=20frac56 end{gather*}
2) Решаем в общем виде.
Все прямые (y=kx+1) проходят через точку (0;1) и при образовании фигуры находятся над параболой.
Точки пересечения прямой и параболы: begin{gather*} kx+1=x^2+2x-3Rightarrow x^2+(2-k)x-4=0\ D=(2-k)^2-4cdot (-4)=(k-2)^2+16gt 0 end{gather*} Дискриминант (Dgt 0) при всех (k). Точки пересечения (пределы интегрирования): $$ x_{1,2}=frac{-(2-k)pmsqrt{D}}{2}=frac{k-2pmsqrt{D}}{2} $$ Разность корней: $$ x_2-x_1=sqrt{D}=sqrt{(k-2)^2+16} $$ Минимальное значение разности корней будет при (k=2).
Площадь: begin{gather*} S(k)=int_{x_1}^{x_2}left((kx+1)-(x^2+2x-3)right)dx=int_{x_1}^{x_2}(-x^2+(k-2)x+4)dx=\ =left(-frac{x^3}{3}+frac{(k-2)x^2}{2}+4xright)|_{x_1}^{x_2}=-frac13(x_2^3-x_1^3)+frac{k-2}{2}(x_2^2-x_1^2)+4(x_2-x_1) end{gather*}

begin{gather*} S(k)_{min}=S(2)\ x_{1,2}=pm 2\ S(2)=-frac13cdot(2^3+2^3)+0+4sqrt{16}=\ =-frac{16}{3}+16=frac{32}{3}=10frac23 end{gather*}

Ответ: 1) (S(-1)=20frac56); 2) (S(k)_{min}=S(2)=10frac23)

Пример 5*. Фигура ограничена линиями (y=(x+3)^2, y=0, x=0). Под каким углом к оси OX надо провести прямые через точку (0;9), чтобы они разбивали фигуру на три равновеликие части?

Площадь криволинейной трапеции AOB: begin{gather*} S_0=int_{-3}^{0}(x+3)^2dx=frac{(x+3)^3}{3}|_{-3}^{0}=\ =9-0=9 end{gather*} Площадь каждой части: (S_i=frac13 S_0=3)
Точки (C(x_1; 0)) и (D(x_2; 0)) c (-3lt x_1lt x_2lt 0) такие, что прямые AC и AD отсекают по 1/3 от фигуры.
Площадь прямоугольного треугольника (triangle AOD): begin{gather*} S_3=frac12|x_2|cdot 9=3Rightarrow |x_2|=frac69=frac23Rightarrow\ x_2=-frac23 end{gather*} Площадь прямоугольного треугольника (triangle AOC): begin{gather*} S_2+S_3=frac12|x_1|cdot 9=6Rightarrow |x_1|=frac{12}{9}=frac43Rightarrow\ x_1=-frac43 end{gather*}

Находим углы соответствующих прямых.
Для (x_1: tgalpha=frac{9}{|x_1|}=frac{9}{4/3}=frac{27}{4}, alpha=arctgfrac{27}{4})
Для (x_x: tgbeta=frac{9}{|x_2|}=frac{9}{2/3}=frac{27}{2}, beta=arctgfrac{27}{2})

Ответ: (arctgfrac{27}{4}) и (arctgfrac{27}{2})

Источник

На чтение 2 мин. Просмотров 43.4k.

Площадь криволинейной трапеции, ограниченной сверху графиком функции y=f (x), снизу — осью Ох, слева и справа прямыми х=a, x=b, находят по формуле Ньютона-Лейбница (ф. Н-Л):

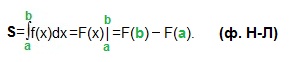
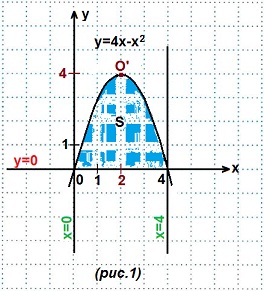Пример 1. Найти площадь криволинейной трапеции, ограниченной линиями: y=4x-x²; y=0; x=0; x=4.

Решение. Строим графики данных линий. (рис. 1).
1) y=4x-x² — парабола (вида y=ax²+bx+c). Запишем данное уравнение в общем виде: y=-x²+4x. Ветви этой параболы направлены вниз, так как первый коэффициент а=-1<0.

Вершина параболы находится

в точке O′(m; n), где

О′(2; 4). Нули функции (точки пересечения графика с осью Ох) найдем из уравнения:

4х-х²=0.

Выносим х за скобки, получаем: х(4-х)=0. Отсюда, х=0 или х=4. Абсциссы точек найдены, ордината равна нулю — искомые точки: (0; 0) и (4; 0).

2) y=0 — это ось Ох; 3) х=0 — это ось Оy; 4) х=4 — прямая, параллельная оси Оy и отстоящая от нее на 4 единичных отрезка вправо.

Площадь построенной криволинейной трапеции находим по (ф. Н-Л). У нас f (x)=4x-x², a=0, b=4.

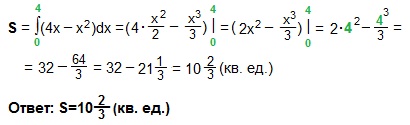
Кстати, если Вы подсчитаете все целые заштрихованные клетки и добавите к ним половину всех остальных клеток заштрихованной фигуры, то получите приближенное значение искомой площади. Действительно, если единичный отрезок равен одной клетке, то площадь квадратика со стороной, равной 1 клетке, равна 1·1=1 (кв. ед.). Сколько квадратиков — столько квадратных единиц и составляет площадь фигуры.

Пример 2. Найти площадь криволинейной трапеции, ограниченной линиями:

Решение. Строим графики данных линий. (рис. 2).

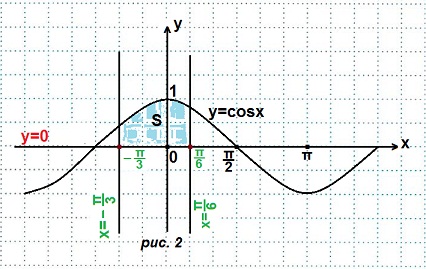
Площадь данной криволинейной трапеции:

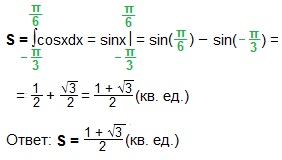
( 11 оценок, среднее 3.55 из 5 )

Источник

Содержание:

Примеры с решением

Рассмотрим функцию , которая непрерывна на отрезке и принимает на этом промежутке неотрицательные значения. Фигуру, ограниченную графиком функции и прямыми , и , называют криволинейной трапецией.

На рисунке 26.1 приведены примеры криволинейных трапеций.

Рассмотрим теорему, которая позволяет вычислять площади криволинейных трапеций.

Теорема 26.1.

Площадь криволинейной трапеции, ограниченной графиком функции и прямыми , и , можно вычислить по формуле

где — любая первообразная функции на отрезке .

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Доказательство. Рассмотрим функцию , где , которая определена таким правилом.

Если , то ; если , то — это площадь криволинейной трапеции, показанной штриховкой на рисунке 26.2.

Докажем, что для всех .

Пусть — произвольная точка отрезка и — приращение аргумента в точке , Ограничимся рассмотрением случая, когда (случай, когда , рассматривают аналогично).

Имеем:

Получаем, что — это площадь криволинейной трапеции, заштрихованной на рисунке 26.3.

На отрезке как на стороне построим прямоугольник, площадь которого равна (рис. 26.4). Длины сторон этого прямоугольника равны и , где — некоторая точка промежутка . Тогда Отсюда

Если , то .

Возможно вам будут полезны данные страницы:

Поскольку функция непрерывна в точке , то . Отсюда, если , то

Имеем

Поскольку — произвольная точка области определения функции , то для любого выполняется равенство . Получили, что функция является одной из первообразных функции на отрезке .

Пусть — некоторая первообразная функции на отрезке . Тогда по основному свойству первообразной можно записать

где — некоторое число.

Имеем:

По определению функции искомая площадь криволинейной трапеции равна . Следовательно,

Примеры с решением

Пример 1.

Найдите площадь фигуры, ограниченной графиком функции и прямыми , и

Решение:

На рисунке 26.5 изображена криволинейная трапеция, площадь которой требуется найти.

Одной из первообразных функции на отрезке является функция Тогда

Пример 2.

Найдите площадь фигуры, ограниченной графиком функции и прямой .

Решение:

График функции пересекает прямую в точках и (рис. 26.6). Тогда фигура, площадь которой требуется найти, является криволинейной трапецией, ограниченной графиком функции и прямыми

Одной из первообразных функции на отрезке является функция Тогда

Определение. Пусть — первообразная функции на промежутке , числа и , где , принадлежат промежутку . Разность называют определенным интегралом функции на отрезке .

Определенный интеграл функции на отрезке обозначают (читают: «интеграл от до эф от икс де икс»). Следовательно,

где — произвольная первообразная функции на промежутке .

Например, функция является первообразной функции на промежутке . Тогда для произвольных чисел и , где , можно записать:

Заметим, что значение разности не зависит от того, какую именно первообразную функции выбрали. Действительно, каждую первообразную функции на промежутке можно представить в виде , где — некоторая постоянная. Тогда

Равенство (1) называют формулой Ньютона—Лейбница. Следовательно, для вычисления определенного интеграла по формуле Ньютона-Лейбница надо:

найти любую первообразную функции на отрезке ;
вычислить значение первообразной в точках и ;
найти разность .

При вычислении определенных интегралов разность обозначают

Используя такое обозначение, вычислим, например, Имеем:

Пример 3.

Вычислите

Решение:

Имеем:

Если функция имеет первообразную на отрезке и , то из формулы Ньютона-Лейбница следует такое свойство определенного интеграла:

Действительно,

Если каждая из функций и имеет первообразную на отрезке , то, используя теоремы 25.1 и 25.2, можно доказать (сделайте это самостоятельно) такие свойства определенного интеграла:

где — некоторое число.

Формула Ньютона-Лейбница позволяет установить связь между определенным интегралом и площадью криволинейной трапеции, ограниченной графиком функции и прямыми , и ().

Используя теорему 26.1, можно записать:

Заметим, что в этой формуле рассматриваются непрерывные функции , которые на отрезке принимают только неотрицательные значения. Однако определенный интеграл можно использовать для вычисления площадей более сложных фигур.

Рассмотрим непрерывные на отрезке функции и такие, что для всех выполняется неравенство

Покажем, как найти площадь фигуры , ограниченной графиками функций и и прямыми и (рис. 26.7).

Перенесем фигуру вверх на единиц так, чтобы полученная фигура находилась выше оси абсцисс (рис. 26.8). Фигура ограничена графиками функций и и прямыми , .

Поскольку фигуры и имеют равные площади, то искомая площадь равна разности

где — площадь криволинейной трапеции, ограниченной графиком функции и прямыми , и (рис. 26.9, а);

— площадь криволинейной трапеции, ограниченной графиком функции и прямыми , и (рис. 26.9, б).

Таким образом, используя свойства определенного интеграла, можем записать:

Следовательно, если функции и непрерывны на отрезке и для всех выполняется неравенство то площадь фигуры, ограниченной графиками функций и и прямыми и , можно вычислить по формуле

Пример 4.

Найдите площадь фигуры, ограниченной графиками функций и

Решение:

На рисунке 26.10 изображена фигура, площадь которой требуется найти.

Решив уравнение , устанавливаем, что графики функций и пересекаются в двух точках с абсциссами и .

Тогда искомая площадь

Лекции:

Экспонента, натуральные логарифмы и гиперболические функции
Непрерывная случайная величина
Математическое ожидание и дисперсия случайной величины
Исследование функции: пример решения
Понятие функции. Теория пределов
Элементарные функции комплексного переменного. Дробно-рациональные функции
Равномерная сходимость функционального ряда
Критерий Сильвестра
Преобразования в пространстве и на плоскости
Площадь поверхности подобных фигур

Источник

Алгебра и начала математического анализа, 11 класс

Урок №23.Площадь криволинейной трапеции. Интеграл и его свойства.

Перечень вопросов, рассматриваемых в теме

1) Нахождение определенного интеграла

2) Нахождение площади криволинейной трапеции с помощью формулы Ньютона – Лейбница

3) Решение задач, с помощью формулы Ньютона – Лейбница

Формула Ньютона – Лейбница

Основная литература:

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Дополнительная литература:

ОрловаЕ. А., СеврюковП. Ф., СидельниковВ. И., СмоляковА.Н.Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.

Теоретический материал для самостоятельного изучения

Криволинейной трапецией называется фигура, ограниченная графиком непрерывной и не меняющей на отрезке [а;b] знака функции f(х), прямыми х=а, x=b и отрезком [а;b].

Отрезок [a;b] называют основанием этой криволинейной трапеции

формула Ньютона – Лейбница

Если в задаче требуется вычислить площадь криволинейной трапеции, то ответ всегда будет положительный. Если требуется, используя чертеж, вычислить интеграл, то его значение может быть любым(зависит от расположения криволинейной трапеции).

Примеры и разбор решения заданий тренировочного модуля

№1.Найти площадь криволинейной трапеции, изображенной на рисунке

Решение

Для вычисления площади криволинейной трапеции воспользуемся формулой Ньютона – Лейбница.

Ответ:

№2. Вычислить определенный интеграл:

Решение: Воспользуемся формулой Ньютона-Лейбница.

Сначала находим первообразную функцию F(x) . Далее подставляем значение верхнего предела в первообразную функцию: F(b) .

Затем подставляем значение нижнего предела в первообразную функцию: F(а).

Рассчитываем разность F(b) – F(а), это и будет ответ.

№3. Найти площадь криволинейной трапеции (х-1)², ограниченной линиями х=2 и х=1, осью 0х

Решение:

Воспользуемся формулой Ньютона-Лейбница.

Сначала находим первообразную функцию F(x). Далее подставляем значение верхнего предела в первообразную функцию: F(b) .

Затем подставляем значение нижнего предела в первообразную функцию: F(а).

Рассчитываем разность F(b) – F(а), это и будет ответ.

Источник

Найдите площадь трапеции, изображенной на рисунке.

Найдите площадь трапеции, изображённой на рисунке.

Найдите площадь трапеции, изображенной на рисунке.

Найдите площадь трапеции, вершины которой имеют координаты (2;1), (10;1), (5;8), (1;8).

Найдите площадь трапеции, вершины которой имеют координаты (2;1), (10;1), (4;9), (1;9).

Найдите площадь трапеции, вершины которой имеют координаты (2;1), (10;1), (6;9), (1;9).

Найдите площадь трапеции, вершины которой имеют координаты (2;1), (10;1), (8;9), (1;9).

Найдите площадь трапеции, изображенной на рисунке.

Найдите площадь трапеции, вершины которой имеют координаты (2;2), (10;2), (4;8), (1;8).

Найдите площадь трапеции, вершины которой имеют координаты (2;2), (10;2), (6;8), (1;8).

Найдите площадь трапеции, вершины которой имеют координаты (2;2), (10;2), (8;8), (1;8).

Найдите площадь трапеции, вершины которой имеют координаты (2;2), (10;2), (5;9), (1;9).

Найдите площадь трапеции, изображенной на рисунке.

100

Найдите площадь трапеции, изображенной на рисунке.

101

Найдите площадь трапеции, изображенной на рисунке.

102

Найдите площадь трапеции, изображенной на рисунке.

103

Найдите площадь трапеции, изображенной на рисунке.

104

Найдите площадь трапеции, изображенной на рисунке.

105

Найдите площадь трапеции, изображенной на рисунке.

106

Найдите площадь трапеции, изображенной на рисунке.

107

Найдите площадь трапеции, вершины которой имеют координаты (2;3), (10;3), (7;8), (1;8).

108

Найдите площадь трапеции, вершины которой имеют координаты (2;3), (10;3), (3;9), (1;9).

109

Найдите площадь трапеции, вершины которой имеют координаты (2;3), (10;3), (5;9), (1;9).

110

Найдите площадь трапеции, вершины которой имеют координаты (2;3), (10;3), (7;9), (1;9).

111

Найдите площадь трапеции, изображенной на рисунке.

112

Найдите площадь трапеции, изображенной на рисунке.

113

Найдите площадь трапеции, изображенной на рисунке.

114

Найдите площадь трапеции, изображенной на рисунке.

115

Найдите площадь трапеции, изображенной на рисунке.

116

Найдите площадь трапеции, изображенной на рисунке.

117

Найдите площадь трапеции, изображенной на рисунке.

118

Найдите площадь трапеции, изображенной на рисунке.

119

Найдите площадь трапеции, изображенной на рисунке.

120

Найдите площадь трапеции, вершины которой имеют координаты (2;4), (10;4), (3;9), (1;9).

121

Найдите площадь трапеции, вершины которой имеют координаты (2;4), (10;4), (7;9), (1;9).

122

Найдите площадь трапеции, изображенной на рисунке.

123

Найдите площадь трапеции, изображенной на рисунке.

124

Найдите площадь трапеции, вершины которой имеют координаты (3;1), (10;1), (6;8), (1;8).

125

Найдите площадь трапеции, вершины которой имеют координаты (3;1), (10;1), (7;8), (2;8).

126

Найдите площадь трапеции, вершины которой имеют координаты (3;1), (10;1), (4;9), (1;9).

127

Найдите площадь трапеции, вершины которой имеют координаты (3;1), (10;1), (6;9), (1;9).

128

Найдите площадь трапеции, вершины которой имеют координаты (3;1), (10;1), (5;9), (2;9).

129

Найдите площадь трапеции, вершины которой имеют координаты (3;1), (10;1), (7;9), (2;9).

130

Найдите площадь трапеции, изображенной на рисунке.

131

Найдите площадь трапеции, изображенной на рисунке.

132

Найдите площадь трапеции, изображенной на рисунке.

133

Найдите площадь трапеции, изображенной на рисунке.

134

Найдите площадь трапеции, изображенной на рисунке.

135

Найдите площадь трапеции, изображенной на рисунке.

136

Найдите площадь трапеции, изображенной на рисунке.

137

Найдите площадь трапеции, изображенной на рисунке.

138

Найдите площадь трапеции, изображенной на рисунке.

139

Найдите площадь трапеции, вершины которой имеют координаты (3;2), (10;2), (3;8), (1;8).

140

Найдите площадь трапеции, вершины которой имеют координаты (3;2), (10;2), (5;8), (1;8).

141

Найдите площадь трапеции, вершины которой имеют координаты (3;2), (10;2), (7;8), (1;8).

142

Найдите площадь трапеции, вершины которой имеют координаты (3;2), (10;2), (9;8), (1;8).

143

Найдите площадь трапеции, вершины которой имеют координаты (3;2), (10;2), (4;8), (2;8).

144

Найдите площадь трапеции, вершины которой имеют координаты (3;2), (10;2), (6;8), (2;8).

145

Найдите площадь трапеции, вершины которой имеют координаты (3;2), (10;2), (8;8), (2;8).

146

Найдите площадь трапеции, вершины которой имеют координаты (3;2), (10;2), (4;9), (1;9).

147

Найдите площадь трапеции, вершины которой имеют координаты (3;2), (10;2), (5;9), (2;9).

148

Найдите площадь трапеции, изображенной на рисунке.

149

Найдите площадь трапеции, изображенной на рисунке.

150

Найдите площадь трапеции, изображенной на рисунке.

151

Найдите площадь трапеции, изображенной на рисунке.

152

Найдите площадь трапеции, изображенной на рисунке.

153

Найдите площадь трапеции, вершины которой имеют координаты (3;3), (10;3), (3;9), (1;9).

154

Найдите площадь трапеции, вершины которой имеют координаты (3;3), (10;3), (5;9), (1;9).

155

Найдите площадь трапеции, вершины которой имеют координаты (3;3), (10;3), (7;9), (1;9).

156

Найдите площадь трапеции, вершины которой имеют координаты (3;3), (10;3), (9;9), (1;9).

157

Найдите площадь трапеции, вершины которой имеют координаты (3;3), (10;3), (4;9), (2;9).

158

Найдите площадь трапеции, вершины которой имеют координаты (3;3), (10;3), (6;9), (2;9).

159

Найдите площадь трапеции, вершины которой имеют координаты (3;3), (10;3), (8;9), (2;9).

160

Найдите площадь трапеции, изображенной на рисунке.

161

Найдите площадь трапеции, изображенной на рисунке.

162

Найдите площадь трапеции, изображенной на рисунке.

163

Найдите площадь трапеции, вершины которой имеют координаты (3;4), (10;4), (4;9), (1;9).

164

Найдите площадь трапеции, вершины которой имеют координаты (3;4), (10;4), (5;9), (2;9).

165

Найдите площадь трапеции, изображенной на рисунке.

166

Найдите площадь трапеции, вершины которой имеют координаты (4;1), (10;1), (5;8), (1;8).

167

Найдите площадь трапеции, вершины которой имеют координаты (4;1), (10;1), (9;8), (1;8).

168

Найдите площадь трапеции, вершины которой имеют координаты (4;1), (10;1), (6;8), (2;8).

169

Найдите площадь трапеции, вершины которой имеют координаты (4;1), (10;1), (7;8), (3;8).

170

Найдите площадь трапеции, вершины которой имеют координаты (4;1), (10;1), (4;9), (1;9).

171

Найдите площадь трапеции, вершины которой имеют координаты (4;1), (10;1), (6;9), (1;9).

172

Найдите площадь трапеции, вершины которой имеют координаты (4;1), (10;1), (8;9), (1;9).

173

Найдите площадь трапеции, вершины которой имеют координаты (4;1), (10;1), (5;9), (2;9).

174

Найдите площадь трапеции, вершины которой имеют координаты (4;1), (10;1), (7;9), (2;9).

175

Найдите площадь трапеции, вершины которой имеют координаты (4;1), (10;1), (9;9), (2;9).

176

Найдите площадь трапеции, вершины которой имеют координаты (4;1), (10;1), (5;9), (3;9).

177

Найдите площадь трапеции, вершины которой имеют координаты (4;1), (10;1), (7;9), (3;9).

178

Найдите площадь трапеции, изображенной на рисунке.

179

Найдите площадь трапеции, изображенной на рисунке.

180

Найдите площадь трапеции, изображенной на рисунке.

181

Найдите площадь трапеции, изображенной на рисунке.

182

Найдите площадь трапеции, изображенной на рисунке.

183

Найдите площадь трапеции, изображенной на рисунке.

184

Найдите площадь трапеции, изображенной на рисунке.

185

Найдите площадь трапеции, изображенной на рисунке.

186

Найдите площадь трапеции, изображенной на рисунке.

187

Найдите площадь трапеции, вершины которой имеют координаты (4;2), (10;2), (6;8), (3;8).

188

Найдите площадь трапеции, вершины которой имеют координаты (4;2), (10;2), (8;8), (3;8).

189

Найдите площадь трапеции, вершины которой имеют координаты (4;2), (10;2), (3;9), (1;9).

190

Найдите площадь трапеции, вершины которой имеют координаты (4;2), (10;2), (4;9), (2;9).

191

Найдите площадь трапеции, вершины которой имеют координаты (4;2), (10;2), (5;9), (3;9).

192

Найдите площадь трапеции, изображенной на рисунке.

193

Найдите площадь трапеции, вершины которой имеют координаты (4;3), (10;3), (4;9), (1;9).

194

Найдите площадь трапеции, вершины которой имеют координаты (4;3), (10;3), (6;9), (1;9).

195

Найдите площадь трапеции, вершины которой имеют координаты (4;3), (10;3), (8;9), (1;9).

196

Найдите площадь трапеции, вершины которой имеют координаты (4;3), (10;3), (5;9), (2;9).

197

Найдите площадь трапеции, вершины которой имеют координаты (4;3), (10;3), (7;9), (2;9).

198

Найдите площадь трапеции, вершины которой имеют координаты (4;3), (10;3), (9;9), (2;9).

199

Найдите площадь трапеции, вершины которой имеют координаты (4;3), (10;3), (5;9), (3;9).

200

Найдите площадь трапеции, вершины которой имеют координаты (4;3), (10;3), (7;9), (3;9).

201

Найдите площадь трапеции, изображенной на рисунке.

202

Найдите площадь трапеции, изображенной на рисунке.

203

Найдите площадь трапеции, изображенной на рисунке.

204

Найдите площадь трапеции, изображенной на рисунке.

205

Найдите площадь трапеции, изображенной на рисунке.

206

Найдите площадь трапеции, вершины которой имеют координаты (4;4), (10;4), (3;9), (1;9).

207

Найдите площадь трапеции, вершины которой имеют координаты (4;4), (10;4), (4;9), (2;9).

208

Найдите площадь трапеции, вершины которой имеют координаты (4;4), (10;4), (5;9), (3;9).

209

Найдите площадь трапеции, изображённой на рисунке.

210

Найдите площадь трапеции, изображенной на рисунке.

211

Найдите площадь трапеции, изображённой на рисунке.

Источник

Определенный интеграл. Площадь криволинейной трапеции

п.1. Теорема о площади криволинейной трапеции

п.2. Формула Ньютона-Лейбница

п.3. Геометрический смысл теоремы Лагранжа о среднем

п.4. Площадь плоской фигуры, ограниченной двумя кривыми

п.5. Примеры

Примеры с решением

Пример 1.

Пример 2.

Пример 3.

Пример 4.

Вам также может понравиться

Как найти заблокированного пользователя вконтакте

Как составить тренировку в зале для парня

Проблемы с колесиком мыши как исправить

Добавить комментарий Отменить ответ