Как найти площадь трапеции на координатной плоскости - Сайт, где вы сможете решить свои вопросы

Трапецию можно представить в виде комбинации двух треугольников и прямоугольника. Площадью трапеции является сумма площадей этих фигур.

Площадь треугольника вычисляется по формуле:

S=frac12ah

где alpha – длина основания; h – высота треугольника.

Длина первого треугольника равна 2 − 1 = 1.

Длина второго треугольника: 10 − 7 = 3.

Высоты обоих треугольников: 8 − 1 = 7.

Площадь первого треугольника:

S_1=frac12cdot7cdot1=3,5

Площадь второго треугольника:

S_2=frac12cdot7cdot3=10,5

Площадь прямоугольника:

S_3=7cdot5=35

Площадь трапеции:

S=S_1+S_2+S_3=3,5+10,5+35=49

Источник

Задания

Версия для печати и копирования в MS Word

Задания Д4 № 60085

Найдите площадь трапеции, вершины которой имеют координаты

Решение.

Это задание ещё не решено, приводим решение прототипа.

Найдите площадь трапеции, вершины которой имеют координаты (2; 2), (8; 4), (8; 8), (2; 10).

Построим трапецию на координатной плоскости. Площадь трапеции равна произведению полусуммы оснований на высоту:

Ответ: 36.

Аналоги к заданию № 27705: 60057 60063 60067 … Все

Кодификатор ФИПИ/Решу ЕГЭ:

5.1.3 Трапеция;

5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора;

5.6.1 Координаты на прямой, декартовы координаты на плоскости и в пространстве.

Прототип задания

Видеокурс

Источник

Вычисление площадей фигур в различных системах координат

Площадь плоской фигуры в декартовых координатах

Напомним, что мы назвали криволинейной трапецией фигуру, ограниченную осью абсцисс, прямыми x=a и x=b и графиком функции y=f(x) . В этом пункте выведем формулу для вычисления площади криволинейной трапеции.

Теорема 3. Если функция y=f(x) неотрицательна на отрезке [a;b] и непрерывна на нем, то соответствующая ей криволинейная трапеция квадрируема, причем ее площадь выражается формулой

${ S= intlimits_{a}^{b} f(x),dx,.}$

(4)

Доказательство. Криволинейная трапеция ограничена тремя отрезками и графиком непрерывной функции y=f(x) . Как было показано в пункте 2 такая фигура квадрируема. Чтобы вычислить площадь этой трапеции, построим для нее внешние и внутренние ступенчатые фигуры (см. рис. 26).

Тогда, с одной стороны, имеем:

$sum_{k=0}^{n-1}m_kDelta x_kleqslant Sleqslant sum_{k=0}^{n-1} M_kDelta x_k,,$

где $sum_{k=0}^{n-1}m_kDelta x_k$ — площадь внутренней ступенчатой фигуры, $sum_{k=0}^{n-1}M_kDelta x_k$ —площадь внешней ступенчатой фигуры, $m_k=min_{xin [x_k;x_{k+1}]}f(x)$ и $M_k=max_{xin[x_k;x_{k+1}]}f(x)$ . С другой стороны, по определению интеграла можно записать:

$sum_{k=0}^{n-1}m_kDelta x_kleqslant intlimits_{a}^{b} f(x),dxleqslant sum_{k=0}^{n-1}M_kDelta x_k,.$

Таким образом, числа и $intlimits_{a}^{b} f(x),dx$ разделяют одни и те же числовые множества: $Biggl{,sum_{k=0}^{n-1}m_kDelta x_k,Biggr},$ $Biggl{,sum_{k=0}^{n-1}M_kDelta x_k,Biggr}$ . Но, как было показано при изучении определенного интеграла, эти множества разделяются лишь одним числом, и потому $S=intlimits_{a}^{b} f(x),dx$ . Теорема доказана.

Аналогично доказывается, что если фигура ограничена снизу графиком функции y=f_1(x) , сверху графиком функции y=f_2(x) , а слева и справа прямыми x=a,~x=b (рис. 30), то ее площадь выражается формулой

$S= intlimits_{a}^{b}bigl[f_2(x)-f_1(x)bigr]dx,.$

Наглядный смысл формулы (4) состоит в том, что криволинейную трапецию можно рассматривать как объединение «бесконечно тонких полосок» с основаниями и высотами f(x) .

Площадь фигуры между двумя графиками функций

Пусть теперь функция y=f(x) непрерывна на отрезке [a;b] и принимает на нем только неположительные значения. Выразим с помощью определенного интеграла площадь соответствующей криволинейной трапеции .

Рассмотрим фигуру Phi , симметричную фигуре относительно оси . Эта фигура (рис. 31) представляет собой криволинейную трапецию, ограниченную сверху графиком непрерывной на отрезке [a;b] функции y=f(x) , которая на [a;b] принимает только неотрицательные значения. По доказанному выше

Интегрирование знакопеременной функции

$S(Phi)= intlimits_{a}^{b} bigl(-f(x)bigr)dx$ . Но S(Phi)=S(F).

Значит,

$S(F)= intlimits_{a}^{b} bigl(-f(x)bigr)dx= -intlimits_{a}^{b} f(x),dx,.$

Как мы видим, в рассматриваемом случае интеграл $intlimits_{a}^{b} f(x),dx$ дает значение площади криволинейной трапеции с точностью до знака. Если же функция меняет знак на отрезке [a;b] в конечном числе точек, то значение интеграла $intlimits_{a}^{b} f(x),dx$ дает алгебраическую сумму площадей соответствующих криволинейных трапеций, ограниченных частями графика функции y=f(x) , отрезками оси и, быть может, отрезками, параллельными оси (рис. 32).

Пример 1. Найти площадь фигуры, ограниченной кривой y=e^x , осью абсцисс и прямыми x=1,~x=2 (рис. 33).

Решение. Имеем: $S= intlimits_{1}^{2} e^x,dx= Bigl.{e^x}Bigr|_{1}^{2}= e^2-e= e(e-1)$ (кв. ед.).

Пример 2. Вычислить площадь фигуры, ограниченной дугой параболы y^2=4x и отрезком прямой x=2 (рис. 34).

Решение. Из рисунка видно, что трапеция, площадь которой нужно найти, расположена симметрично относительно оси абсцисс и, следовательно, искомая площадь равна

$S= 2int_{0}^{2}2sqrt{x},dx= left.{frac{4x^{3/2}}{3/2}}right|_{0}^{2}= frac{8}{3}cdot 2^{3/2}= frac{16}{3}sqrt{2},.$

Пример 3. Найти площадь фигуры, ограниченной графиками функций y^2=9x,~ y=3x (рис. 35).

Решение. Искомая площадь равна разности площадей криволинейного треугольника OAB и прямоугольного треугольника OAB:

$S= intlimits_{0}^{1} sqrt{9x},dx- intlimits_{0}^{1} 3x,dx= left.{3cdot frac{x^{3/2}}{3/2}}right|_{0}^{1}- left.{3cdot frac{x^2}{2} }right|_{0}^{1}= 2-frac{3}{2}= frac{1}{2},.$

Площадь фигуры, ограниченной кривой, осью абсцисс и двумя прямыми

Пример 4. Вычислить площадь фигуры, ограниченной петлей кривой a(y^2-x^2)+x^3=0 .

Решение. Из уравнения кривой видно, что она расположена симметрично относительно оси . Следовательно, можно сначала вычислить половину искомой площади (рис. 36). Рекомендуем читателю подробно исследовать и построить данную кривую.

Площадь фигуры, ограниченной петлёй кривой

Записав уравнение кривой в виде $y^2=frac{x^2}{a}(a-x)$ , найдем точки пересечения ее с осью , положив y=0colon, x_1=0,~ x_2=a . Учитывая сказанное, найдем площадь половины петли:

$frac{1}{2}S= frac{1}{sqrt{a}} intlimits_{0}^{a} xsqrt{a-x},dx,.$

Воспользовавшись формулой из таблицы при a=-1,~ b=a , получим:

$intlimits_{0}^{a} xsqrt{a-x},dx= left.{frac{2(-3x-2a)sqrt{(a-x)^3}}{15}}right|_{0}^{a}= frac{4}{15},a^{5/2},.$

Значит, окончательно имеем:

$frac{1}{2}S= frac{1}{sqrt{a}}cdot frac{4}{15},a^{5/2}= frac{4}{15},a^2quad Leftrightarrowquad S=frac{8}{15},a^2,.$

Площадь фигуры, ограниченной кривой, заданной параметрически

Пусть кривая y=f(x),~ f(x)geqslant0,~ aleqslant xleqslant b задана в параметрической форме

$begin{cases}x=varphi(t),\ y=psi(t),end{cases} alpha leqslant tleqslant b,,$

где функция x=varphi(t) монотонна на отрезке [alpha;beta] , причем varphi(alpha)=a, varphi(beta)=b , и имеет на этом отрезке непрерывную производную. Так как y=f(x)= fbigl(varphi(t)bigr)= psi(t) , то по формуле замены переменной под знаком определенного интеграла получаем:

$S= intlimits_{a}^{b} f(x),dx= intlimits_{alpha}^{beta} fbigl(varphi(t)bigr) varphi'(t),dt= intlimits_{alpha}^{beta} psi(t) varphi'(t),dt,.$

Итак, площадь фигуры, ограниченной кривой, заданной параметрически, вычисляется по формуле:

$S= intlimits_{alpha}^{beta} psi(t)varphi'(t),dt,.$

(5)

Пример 5. Вычислить площадь эллипса, заданного параметрически $begin{cases} x=acos{t},,\ y=bsin{t},,end{cases} 0leqslant tleqslant 2pi,.$

Площадь фигуры, ограниченной эллипсом

Решение. Выберем ту часть эллипса (рис. 37), которая расположена в первом квадранте. Точке A(a;0) соответствует значение t=0 , а точке B(0;b) — значение $t=frac{pi}{2}$ . Поэтому

$begin{aligned} S&= 4intlimits_{0}^{a}y,dx= -4intlimits_{0}^{pi/2}bsin{t}cdot(-asin{t}),dt= 4abintlimits_{0}^{pi/2} sin^2t,dt=\ &= 2abintlimits_{0}^{pi/2} bigl(1-cos2tbigr),dt= left.{2ab!left(t- frac{1}{2}sin2t right)}right|_{0}^{pi/2}= pi,ab,. end{aligned}$

Площадь фигуры, заданной в полярных координатах

Вычислить площадь сектора, ограниченного лучами ell и , выходящими из точки , и непрерывной кривой Gamma (рис. 38). Выберем полярную систему координат, полюсом которой является точка . Пусть rho=rho(varphi) — полярное уравнение кривой Gamma , а varphi_0 и Phi — углы между полярной осью и лучами ell и соответственно. При этом пусть функция непрерывна на [varphi_0;Phi] .

Разобьем данный сектор на частей лучами

$varphi_0< varphi_1< varphi_2< ldots< varphi_k< varphi_{k+1}< ldots< varphi_n= Phi$

и рассмотрим k-й частичный сектор $[varphi_k; varphi_{k+1}]$ (рис. 39). Пусть r_k — наименьшее значение функции rho(varphi) в $[varphi_k; varphi_{k+1}]$ , a R_k — наибольшее значение функции в этом отрезке.

Площадь в полярных координатах и разбиение сектора на n частей

Построим два круговых сектора с радиусами r_k и R_k . Обозначим через Deltavarphi_k величину угла рассматриваемого частичного сектора. Тогда площадь частичного криволинейного сектора будет заключена между площадями вписанного и описанного частичных круговых секторов

$frac{1}{2}cdot r_k^2cdot Deltavarphi_k leqslant S_kleqslant frac{1}{2}cdot R_k^2cdot Deltavarphi_k,.$

Построим аналогичным образом внутренние и внешние круговые секторы для всех частичных криволинейных секторов. Объединяя их, получим внутреннюю и внешнюю фигуры.

Площадь внутренней фигуры, состоящей из круговых секторов, равна $frac{1}{2} sum_{k=0}^{n-1} r_k^2 Deltavarphi_k$ , а площадь внешней фигуры равна — $frac{1}{2} sum_{k=0}^{n-1} R_k^2 Deltavarphi_k$ . Эти выражения являются нижней и верхней суммами Дарбу s_P и S_P для интеграла $frac{1}{2} intlimits_{varphi_0}^{Phi} rho^2(varphi),dvarphi$ . Так как функция rho(varphi) непрерывна, то непрерывна, а потому и интегрируема функция . Поэтому для любого varepsilon найдется такое разбиение отрезка [varphi_0,Phi] , что S_P-s_P<varepsilon . Из теоремы 2 пункта 2 следует, что заданный криволинейный сектор квадрируем. При этом для его площади выполняются неравенства

Площадь, ограниченная одним лепестком полярной розы

$frac{1}{2} sum_{k=0}^{n-1} r_k^2 Deltavarphi_kleqslant Sleqslant frac{1}{2} sum_{k=0}^{n-1} R_k^2 Deltavarphi_k,.$

(6)

В то же время по определению определенного интеграла

$frac{1}{2} sum_{k=0}^{n-1} r_k^2 Deltavarphi_kleqslant frac{1}{2} intlimits_{varphi_0}^{Phi} rho^2(varphi),dvarphi leqslant frac{1}{2} sum_{k=0}^{n-1} R_k^2 Deltavarphi_k,.$

(7)

В силу единственности разделяющего числа из неравенств (6) и (7) следует, что

$S= frac{1}{2} intlimits_{varphi_0}^{Phi} rho^2(varphi),dvarphi,.$

(8)

Пример 6. Вычислить площадь, ограниченную одним лепестком розы rho=asin2varphi (рис. 40).

Решение. Значениям varphi=0 и $varphi=frac{pi}{2}$ соответствует rho=0 Поэтому

$S= frac{1}{2} intlimits_{0}^{pi/2} a^2sin^22varphi,dvarphi= frac{a^2}{2} intlimits_{0}^{pi/2} frac{1-cos4varphi}{2},dvarphi= left.{frac{a^2}{4}! left(varphi- frac{1}{4}sin4varphiright)}right|_{0}^{pi/2}= frac{a^2}{4}cdot frac{pi}{2}= frac{pi}{2},a^2,.$

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Площадь по заданным координатам.

Как найти (вычислить) площадь фигуры (треугольник, четырехугольник, трапеция, многоугольник и др.) по координатам?

Какие есть формулы и методы, позволяющие находить площадь через координаты?

бонус за лучший ответ (выдан): 5 кредитов

Для вычисления площади простого многоугольника с любым количеством вершин, представленных в виде списка координат, при последовательном обходе которых, не образуются пересекающиеся линии, применяется формула Гаусса, иначе называемая “формулой землемера”, “формулой геодезиста”, “формулой шнурования”, “алгоритмом шнурования”, а так же “методом треугольников”.

Суть метода заключается в построении треугольников, состоящих из сторон многоугольника и лучей проведённых из начала координат к вершинам многоугольника, и сложении площадей треугольников, включающих внутреннюю часть многоугольника с вычитанием площадей треугольников, расположенных снаружи.

Площадь, вычисленная по приведенной формуле, будет иметь отрицательное значение при обходе фигуры по часовой стрелке и положительное при обходе против часовой стрелки.

Фигура многоугольника может иметь произвольную геометрию. Например:

Список координат многоугольника представлен в виде массива: (x1, y1), (x2, y2), (x3, y3),…(xn, yn).

Для многоугольника на первом рисунке он задан точками: (3,4), (5,11), (12,8), (9,5), (5,6). Его площадь будет равна:

Существует также метод трапеций, основанный на сложении и вычитании площадей трапеций, образованных каждой из сторон многоугольника, её проекцией на ось абсциссы и перпендикулярами, опущенных из вершин на абсциссу. При обходе вершин по часовой стрелке учитывается величина координаты вершин. Если первая вершина меньше второй, то площадь трапеции прибавляется, если нет, то отнимается.

Для многоугольника ABCDE на левом нижнем рисунке существует 5 трапеций : ABJH, CBJF, CDIF, EDIG и EAHG.

Так как X1<X2, X3<X4 и X5<X1, то площади трапеций ABJH, CDIF и EAHG складываются, а X3>X4 и X4<X5, следовательно, площади трапеций CBJF и EDIG вычитаются:

S = S(ABJH) – S(CBJF) + S(CDIF) – S(EDIG) + S(EAHG)

Площади трапеций рассчитываются по формуле;

Sтрапеции = 1/2 *((a+b))*h,

где a, b – основания трапеции,

h – высота трапеции.

Значения a, b и h вычисляются по координатам.

В декартовых координатах круг может быть представлен двумя точками: центр А и любая точка В, лежащая на окружности. Для расчета площади круга необходимо вычислить его радиус по формуле:

автор вопроса выбрал этот ответ лучшим

Ксарфакс
[156K]

5 лет назад

Площадь фигуры по координатам вершин

Если известны координаты всех вершин, то площадь заданной геометрической фигуры (треугольника, прямоугольника, трапеции, ромба и т.д) можно найти по стандартным формулам. Но предварительно нужно найти длину сторон, диагоналей и т.п. (всё зависит от фигуры) с помощью формулы нахождения длины отрезка по заданным координатам.

Эта формула выглядит следующим образом:

Здесь:

AB – отрезок,

точка A имеет координаты (x1, y1),

точка B имеет координаты (x2, y2).

Рассмотрим несколько примеров.

1) Треугольник ABC имеет координаты A(2,3); B(6,7); C(5,0). Его площадь можно найти по формуле Герона:

Здесь:

S – площадь треугольника,

a, b, c – стороны,

p – полупериметр, который равен половине суммы сторон a, b и c.

Найдём, чему равны стороны треугольника по формуле нахождения длины отрезка по координатам:

AB = √(4² + 4²) = √32 ≈ 5,66.

AC = √(3² + (-3)²) = √18 ≈ 4,24.

BC = √((-1)² + (-7)²) = √50 ≈ 7,07.

Полупериметр треугольника будет равен (5,66 + 4,24 + 7,07) / 2 ≈ 16,97 / 2 ≈ 8,49.

Отсюда площадь треугольника ABC ≈ √(8,49 * 2,83 * 4,25 * 1,42) ≈ √145 ≈ 12,04.

2) Ромб ABCD имеет координаты A(1,2); B(3,4); C(5,2); D(3,0). Площадь можно найти через диагонали:

Здесь:

S – площадь ромба,

d1 и d2 – диагонали.

Таким образом, нам нужно найти диагонали AC и BD.

AC = √(4² + 0) = √16 = 4.

BD = √(0 + (-4)²) = √16 = 4.

Отсюда площадь ромба ABCD = 0,5 * 4 * 4 = 8.

3) Трапеция ABCD имеет координаты A(1,1); B(3,4); C(5,4); D(6,1). Стандартная формула площади трапеции такая:

Здесь:

S – площадь трапеции,

a и b – основания,

h – высота.

Высота трапеции (пусть это будет BE) – это перпендикуляр, который был опущен из вершины трапеции (из точки B) на её основание (в нашем случае это AD).

Определим координаты её отрезка:

координаты первой точки совпадают с точкой B, это (3,4).
координаты 2 точки (точка E) будут (3,1) – так как абсцисса совпадает с абсциссой точки B, а ордината совпадает с ординатой точек A и D.

Высота трапеции BE = √(0 + (-3)²) = √9 = 3.

Теперь посчитаем длину оснований:

BC = √(2² + 0) = √4 = 2.

AD = √(5² + 0) = √25 = 5.

Таким образом, площадь трапеции ABCD = 3 * 0,5 * (2 + 5) = 10,5.

Степан-16
[34.5K]

5 лет назад

Первоначально нужно вычислить длины сторон. В этом здесь будет основная задача. Получив стороны, вычисляем площади по стандартным формулам.

Самый простой случай – для прямоугольника, когда его стороны параллельны осям координат. Тогда одна сторона будет равна разнице абсцисс, вторая ординат.

Треугольник. Допустим, основание параллельно оси абсцисс. Вычисляем его длину, как разницу абсцисс. Далее нужно найти высоту. Она будет равна разнице ординат третьей вершины и ординаты любой из вершин основания. Затем – площадь по формуле: половина произведения основания на высоту.

И т.д.

Если же стороны фигуры не параллельны осям, то находить длины сторон придется уже более сложными расчетами. Допустим, прямоугольник. Первую сторону будем искать, как если бы она была гипотенузой в составе прямоугольного треугольника. Каждая сторона будет равна квадратному корню из суммы квадратов абсцисс и ординат концов отрезков стороны.

Так и для любой фигуры. Вначале определяем длины сторон как гипотенузу треугольника. После чего применяем стандартные формулы площадей.

Эления
[445K]

3 года назад

Рассчитать площадь какой угодно геометрической фигуры, зная координаты, не составляет сложности. Каждая из точек, соответствующая вершинам искомой фигуры, будь это треугольник, четырех- или многоугольник, имеет определенную координату, а значит у нее есть значение, через которое можно рассчитать площадь.

Координаты, как найти на графике, чтобы узнать площадь фигуры? Проецируем на оси абсцисс и ординат прямые, проведя перпендикуляр из каждой точки. Полученные значения будут исходной величиной. Каждая из сторон фигуры – это разница двух точек на горизонтальную и вертикальную оси. Разница между значениями означает длину стороны фигуры. А зная все стороны и их значение, по формуле находим площадь.

Пример 1. Ищем площадь треугольника.

Мы видим два отрезка зеленого цвета AB и BC, которые образуют стороны равнобедренного треугольника, а основание есть отрезок на оси абсцисс AC.

Даны значения: AC основание в промежутке от “-4” до “+4”, то есть длина основания равна восьми.

Будет лучше, если посчитать площадь этого треугольника, как сумму из образовавших его двух треугольников, которые являются прямыми, ABO и BOC, совпадающие прямым углом с координатой “0” на графике.

Известна длина каждй из сторон, образующих прямой угол (AO или OC) х = 4 – 0 = 4 и y = 2 – 0 = 2 (BO).

Зная длину двух сторон, образующих прямой угол (AO и BO), находим длину основания (AB или BC). Тогда уже знаем все длины каждой из сторон обоих прямых треугольников. Остается только найти площадь по формуле:

Зная площадь каждого из прямых треугольников, умножаем на два, получаем сумму заштрихованного треугольника на графике ABC.

И еще математически можно записать решение следующим образом, исходя из того, что имеем изначально следующую систему неравенств:

Пример 2.

Пример 3. Есть парабола, ищем площадь фигуры, ограниченную кривой параболы. Чтобы посчитать, используем интеграл.

Бекки Шарп
[71.2K]

3 года назад

Рассмотрим простой случай, где буквально на пальцах можно посчитать площадь через обычную формулу, а затем применим к этой задаче формулу Гаусса.

У нас есть трапеция, у которой известны координаты вершин. (3:2) (5:2) (9:6) (6:6). Мы знаем, что площадь трапеции равна сумме оснований, деленной на 2 и умноженной на высоту.

S = (a+b)/2 х h Считаем площадь: S = (3+2):2х4 = 10. Ответ – 10.

А теперь по теореме Гаусса.

Не смотря на страшный вид, формула очень простая. В квадратных скобках мы перемножаем абсциссу первой точки с ординатой второй, прибавляем абсциссу второй, умноженную на ординату третьей и так идем по кругу фигуры. Далее вычитаем ординату первой умноженную на абсциссу второй и т.д. В квадратных скобках у нас может получиться отрицательное число.

S= 0,5 х [3х6+6х6+9х2+5х2 – 2х6-6х9-6х5-2х3] = 10

Таким образом можно найти площадь любой сложной фигуры, зная ее координаты.

dydySacha
[10.8K]

5 лет назад

Можно взять милиметровку и нанести точки с заданными координатами, согласно осей абсцис и ординат. Соединить эти точки между собой и замерить длины образовавшихся сторон, а с помощью формулы по определению площади образовавшейся фигуры узнать её значение подставив данные в эту формулу.

Алиса в Стране
[363K]

3 года назад

Существует специальная формула, называемая формулой Гаусса, она и позволит нам определить искомую площадь по координатам. Вот как эта формула выглядит:

Формула выглядит немного устрашающе, но давайте попробуем в ней разобраться. У нас есть многоугольник и есть его координаты, подсчитать n – количество сторон многоугольника несложно, а дальше просто нужно подставлять значения в эту формулу, нужно только быть внимательным и не перепутать какие координаты куда надо писать.

Давайте теперь приведем пример нахождения такой площади через формулу Гаусса. Допустим, у нас есть вот такой пятиугольник:

Координаты его пяти вершин, как мы видим: (3, 4), (5, 11), (12, 8), (9, 5), (5, 6).

Теперь нам остается только очень внимательно подставить эти координаты в нашу формулу, n = 5, координаты известны, вот что у нас получится:

Когда разбираешься в этой формуле, понимаешь, насколько она проста и даже легко запоминается, несмотря на то, что сначала кажется очень сложной.

duselldorf
[4.3K]

5 лет назад

Для вычисления площади геометрической фигуры по координатам ее вершин, нужно воспользоваться формулой Гаусса, иногда ее называют формулой землемера или формулой геодезиста, так как она применяется геодезистами для определения площади земельного участка, например, при межевании:

где

А – площадь многоугольника с заданными координатам его вершин,

n – количество сторон многоугольника,

(xi, yi) – координаты вершин многоугольника,

i = 1, 2,…, n — номер вершины многоугольника.

Бархатные лапки
[382K]

3 года назад

Находим площадь вот такого несложного четырехугольника. Координаты его вершин нам известны. Применяем формулу Гаусса, которая выглядит так:

S (площадь) = 0,5 [6х4 +9х7 + 10х6 + 7х3 – 3х9 – 4х10 – 7х7 – 6х6] = 8 (квадратных единиц)

Как видим если применять при решении формулу Гаусса то решить такую задачку несложно.

Не вижу здесь серьезных проблем. Мы, как я понял, имеем готовые точки координат, которые нужно проставить на координатной плоскости. Далее, соединяя эти точки, получаем фигуру, как в примере вопроса – квадрат, треугольник и т.п.

Теперь вычисляем площадь любой из полученных фигур по формуле ей соответствующей.

Знаете ответ?

Источник

Санкт-Петербургский

государственный
университет

аэрокосмического
приборостроения

Пятигорский
филиал

Методическое
пособие

г.
Пятигорск

2011

ВВЕДЕНИЕ

Данное
пособие предназначено для подготовки
к выполнению задания ЕГЭ по математике.
Его целями являются:

– показ
примерной тематики и уровня трудности
геометрических задач, включенных в
содержание ЕГЭ;

– проверка
качества знаний и умений учащихся по
геометрии, их готовность к сдаче ЕГЭ;

– развитие
представлений учащихся об основных
геометрических фигурах и их свойствах,
формирование навыков работы с рисунком;

– повышение
вычислительной культуры учащихся,
подготовка их к решению геометрических
задач с числовым ответом.

Пособие
содержит задачи на нахождение площадей
плоских фигур, нарисованных на клетчатой
бумаге или расположенных на координатной
плоскости. Наличие рисунков помогает
лучше понять условия задач, представить
соответствующую геометрическую
ситуацию, наметить план решения, при
необходимости провести дополнительные
построения и вычисления.

Для
решения предлагаемых задач требуются
знания формул площадей треугольников,
параллелограммов, трапеций, круга и
его частей, умения применять эти формулы
для нахождения площадей фигур, находить
площадь фигуры методом разбиения ее
на более простые фигуры.

Вначале
предлагается диагностическая работа
на нахождение площадей фигур различных
видов: треугольников, параллелограммов,
трапеций, выпуклых и невыпуклых
четырехугольников, круга и его частей,
фигур на координатной плоскости.

Для
тех, кто хочет проверить правильность
решения предложенных задач или убедиться
в верности полученного ответа, приводятся
решения задач, как правило, двумя
различными способами и даются ответы.

Затем,
для закрепления рассмотренных методов
решения задач, предлагаются тренировочные
работы на нахождение площадей для
каждого из перечисленных выше видов
фигур.

В
случае успешного решения этих задач
можно переходить к выполнению
заключительных самостоятельных работ.

В
конце пособия даны ответы ко всем
задачам.

По
аналогии с рассмотренными задачами
можно самим придумывать и решать задачи
на нахождение площадей фигур.

Отметим,
что лучшим способом подготовки к ЕГЭ
по геометрии являются систематические
занятия по учебнику геометрии. Данное
пособие не заменяет учебника. Оно может
быть использовано в качестве
дополнительного сборника задач при
изучении геометрии в 7-9 классах, а также
при организации обобщающего повторения
в 10-11 классах или при самостоятельных
занятиях по геометрии.

Примеры решения задач.

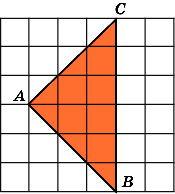
1.
Найдите площадь треугольника ABC,
считая стороны квадратных клеток
равными 1.

Первое
решение.
Заметим, что данный треугольник ABC
является
прямоугольным (A
= 90^о).
Воспользуемся тем, что диагональ
квадратной клетки со сторонами, равными
1, равна .
Тогда катеты AB
и
AC
данного
треугольника будут равны .
Так как площадь прямоугольного
треугольника равна половине произведения
его катетов, то площадь данного
треугольника будет равна ,
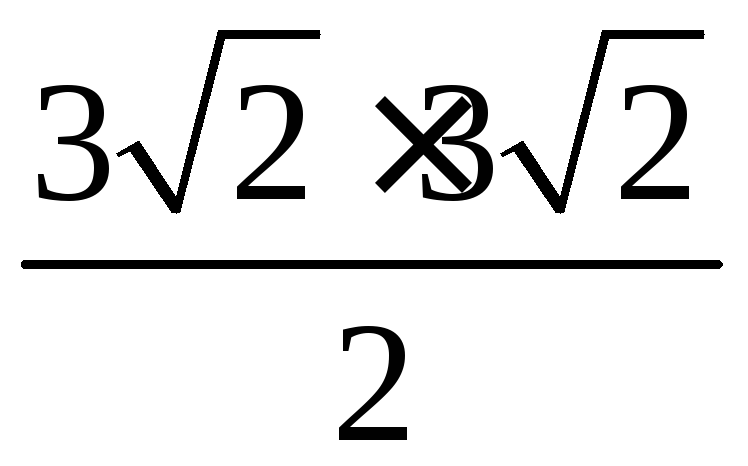т.е. равна 9.

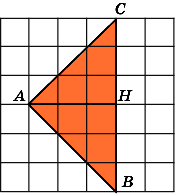
Второе
решение.
Проведем высоту AH.
Тогда BC
= 6,
AH
= 3
и, следовательно, .

Ответ.
9.

2.
Найдите площадь треугольника ABC,
считая стороны квадратных клеток
равными 1.

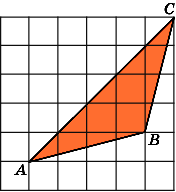
Первое
решение.
Так как диагональ квадрата со стороной
1 равна ,
то сторона AC
треугольника
ABC
равна
,
высота BH,
проведенная к этой стороне, равна .
Следовательно, площадь данного
треугольника равна ,
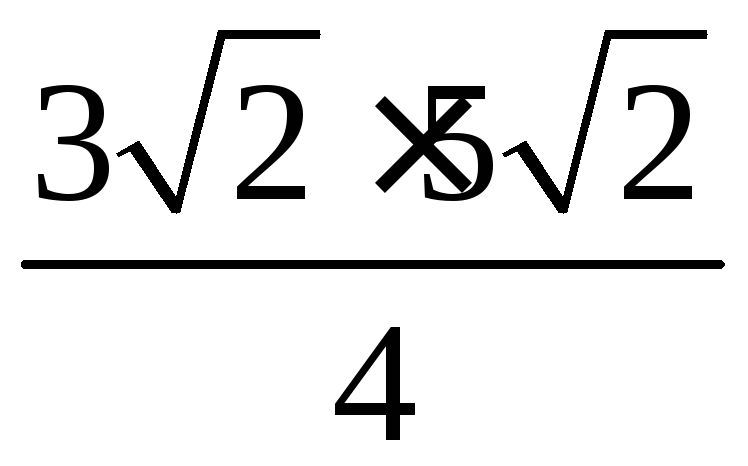т.е. равна 7,5.

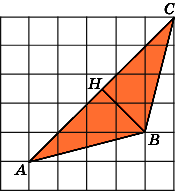
Второе
решение.
Разобьем данный треугольник ABC
на
два треугольника ABD
и
BDC.
Их общая сторона BD
равна
3, а высоты, к ней проведенные, равны
соответственно 1 и 4. Площадь треугольника
ABD
равна
1,5, а площадь треугольника BDC
равна
6. Площадь треугольника ABC
равна
сумме площадей этих треугольников и,
следовательно, равна 7,5.

Ответ.
7,5.

3.
Найдите площадь прямоугольника ABCD,
считая стороны квадратных клеток
равными 1.

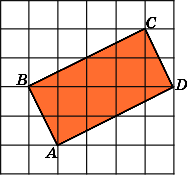
Первое
решение.
Найдем стороны данного прямоугольника.
Рассмотрим прямоугольный треугольник
ADE.
Катет
AE
равен
4, катет DE
равен
2. Следовательно, по теореме Пифагора
гипотенуза AD
равна
.
Аналогично, для прямоугольного
треугольника ABF
катет
AF
равен
1, катет BF
равен
2, Следовательно, по теореме Пифагора
гипотенуза AB
равна
.
Так как площадь прямоугольника равна
произведению его смежных сторон, то
площадь данного прямоугольника будет
равна ,
т.е. равна 10.

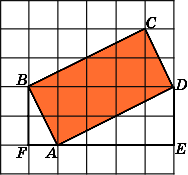
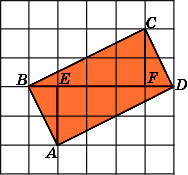
Второе
решение.
Разобьем данный прямоугольник ABCD
на
два треугольника ABD
и
BCD.
Сторона BD
у
них общая и равна 5. Высоты AE
и CF,
опущенные на эту сторону, равны 2. Так
как площадь треугольника равна половине
произведения стороны на высоту, опущенную
на эту сторону, то площадь каждого из
этих двух треугольников будет равна 5
и, следовательно, площадь прямоугольника
будет равна 10.

Ответ.
10.

4.
Найдите площадь ромба ABCD,
считая стороны квадратных клеток
равными 1.

4.
Первое
решение.
Напомним, что площадь ромба равна
половине произведения его диагоналей.
Воспользуемся тем, что диагональ
квадратной клетки со сторонами, равными
1, равна .
Тогда диагонали AС
и
BD
данного
ромба будут равны соответственно
и ,
а его площадь будет равна ,
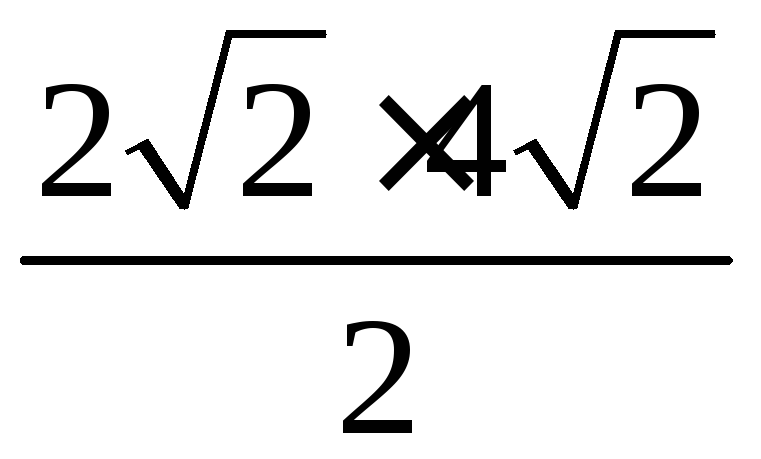т.е. равна 8.

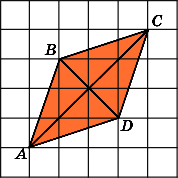
Второе
решение.
Достроим на сторонах ромба четыре
равных прямоугольных треугольника,
катеты которых равны 1 и 3. Площадь
каждого такого треугольника равна 1,5.
Ромб вместе с этими треугольниками
образует фигуру, состоящую из четырнадцати
единичных квадратов. Следовательно,
ее площадь равна 14. Вычитая из нее
площадь четырех треугольников, получим,
что площадь ромба равна 8.

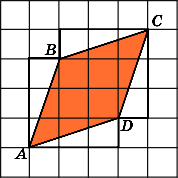
Ответ.
8.

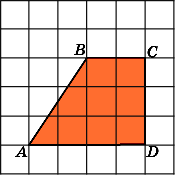
5.
Найдите площадь трапеции ABCD,
считая стороны квадратных клеток
равными 1.

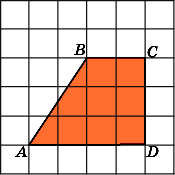
5.
Первое
решение.
Основания AD
и
BC
данной
трапеции равны соответственно 4 и 2.
Высотой является боковая сторона CD.
Она равна 3.
Так
как площадь трапеции равна произведению
полусуммы оснований на высоту, то
площадь данной трапеции будет равна
,
т.е. равна 9.

Второе
решение.
Из точки B
опустим
перпендикуляр BH
на
AD.
Он разобьет трапецию на прямоугольный
треугольник ABH
и
прямоугольник HBCD.
Катеты прямоугольного треугольника
равны 2 и 3, следовательно, его площадь
равна 3. Смежные стороны прямоугольника
равны 2 и 3, следовательно, его площадь
равна 6. Площадь трапеции равна сумме
площадей треугольника и прямоугольника
и, следовательно, равна 9.

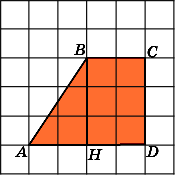
Ответ.
9.

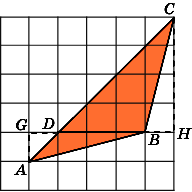
6. Найдите площадь трапеции abcd, считая стороны квадратных клеток равными 1.

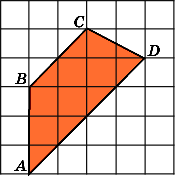
6.
Первое
решение.
Основания AD
и
BC
трапеции
равны соответственно
и .
Высота BH
трапеции
равна .
Так как площадь трапеции равна
произведению полусуммы оснований на
высоту, то площадь данной трапеции
будет равна
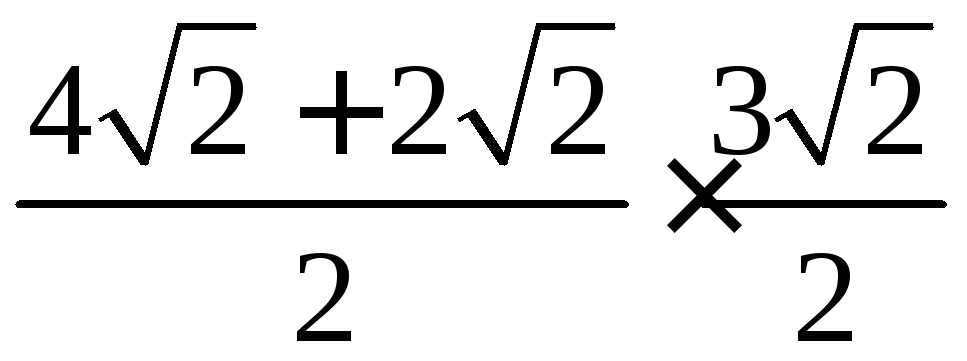
и, следовательно, будет равна 9.

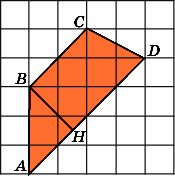
Второе
решение.
Разобьем трапецию на параллелограмм
ABCE
и
треугольник CDE.
Сторона AB
параллелограмма
ABCE
равна
3, высота EH,
к ней проведенная, равна 2, следовательно,
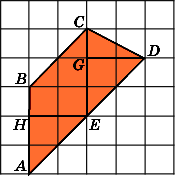
площадь этого параллелограмма равна
6. Сторона CE
треугольника
CDE
равна
3, высота DG,
к ней проведенная, равна 2, следовательно,
площадь этого треугольника равна 3.
Площадь трапеции равна сумме площадей
параллелограмма и треугольника и,
следовательно, равна 9.

Ответ.
9.

7.
Найдите площадь четырехугольника ABCD,
считая стороны квадратных клеток
равными 1.

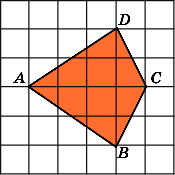
Первое
решение.
Разобьем данный четырехугольник на
два треугольника ABC
и
ACD.
Сторона AC
у
них общая и равна 4. Высоты BH
и
DH
равны
2. Следовательно, площади этих треугольников
равны 4 и, значит, площадь четырехугольника
равна 8.

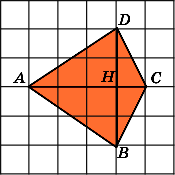
Второе
решение.
Разобьем данный четырехугольник на
два треугольника ABD
и
BCD.
Сторона BD
у
них общая и равна 4. Высоты AH
и
CH
равны
соответственно 3 и 1. Следовательно,
площади этих треугольников равны
соответственно 6 и 2. Значит, площадь
четырехугольника равна 8.

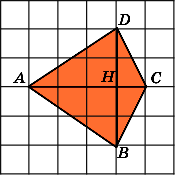
Ответ.
8.

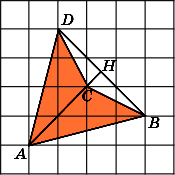
8.
Найдите площадь четырехугольника ABCD,
считая стороны квадратных клеток
равными 1.

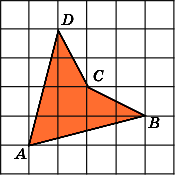
Первое
решение.
Разобьем данный четырехугольник на
два треугольника ACB
и
ACD.
Сторона AC
у
них общая и равна .
Высоты BH
и
DH
равны
.
Следовательно, площади этих треугольников
равны 3. Значит, площадь четырехугольника
равна 6.

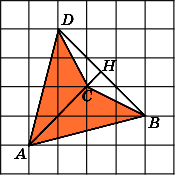
Второе
решение.
Площадь данного четырехугольника равна
разности площадей треугольников ABD
и
CBD.
В треугольнике ABD
сторона
BD
равна
,
высота AH
равна .
Следовательно, его площадь равна 7,5. В
треугольнике CBD
сторона
BD
равна
,
высота CH
равна .
Следовательно, его площадь равна 1,5.
Таким образом, площадь данного
четырехугольника равна 6.

Ответ.
6.

9.
Найдите площадь S
сектора,
считая стороны квадратных клеток
равными 1. В ответе укажите .

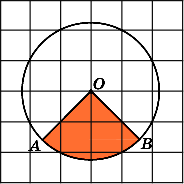
Первое
решение.
Напомним, что площадь S
кругового
сектора вычисляется по формуле ,
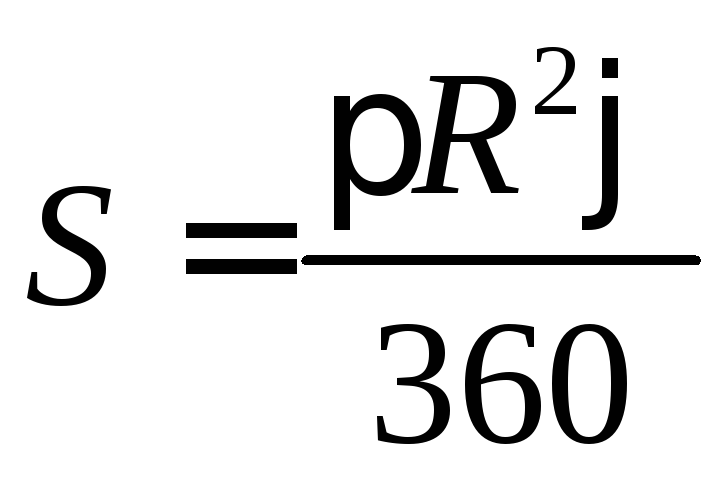где R
–
радиус круга,
– градусная величина угла сектора. В
нашем случае
= 90^о.
Радиус R
равен
.
Подставляя данные
значения
R

и
в формулу площади сектора, получим S
= .
Откуда .

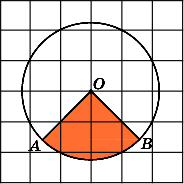
Второе
решение.
Заметим, что данный сектор является
одной четвертой частью круга и,
следовательно, его площадь равна одной
четвертой площади круга. Площадь круга
равна ,
где R
–
радиус круга. В нашем случае R
=и,
следовательно, площадь S
сектора
равна
.
Откуда .

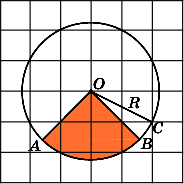
Ответ.
1,25.

10.
Найдите площадь S
кольца,
считая стороны квадратных клеток
равными 1. В ответе укажите

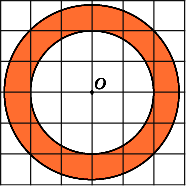
Площадь
кольца равна разности площадей внешнего
и внутреннего кругов. Радиус R
внешнего
круга равен
3,
радиус r
внутреннего
круга равен 2. Следовательно, площадь
S
кольца
равна ,
т.е. S
=
и,
следовательно,

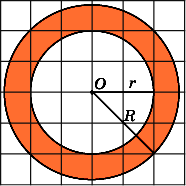
Ответ.
5.

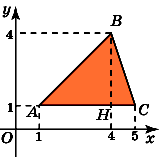
11.Найдите площадь треугольника, вершины
которого имеют координаты (1, 1), (4, 4), (5,
1).

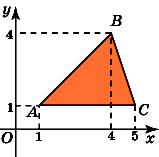
Из
вершины B треугольникаABC опустим высотуBH. Она равна 3. СторонаAC равна 4.
Следовательно, площадь треугольника
равна 6.

Ответ.
6.

12.
Найдите площадь четырехугольника,
вершины которого имеют координаты

(1,
0), (0, 2), (4, 4), (5, 2).

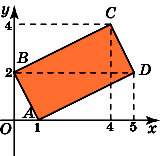
Разобьем
четырехугольник ABCD
на
два треугольника ABD
и
BCD.
Высоты AG
и
CH
этих
треугольников, опущенные на сторону
BD,
равны
2,
сторона BD
равна
5. Следовательно, площади этих треугольников
равны 5 и, значит, площадь четырехугольника
ABCD
равна
10.

Ответ.
10.

Задания для тренировки.

1.
Площадь треугольника

1.
Найдите площадь треугольника ABC,
считая стороны квадратных клеток
равными 1.

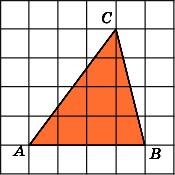
2.
Найдите площадь треугольника ABC,
считая стороны квадратных клеток
равными 1.

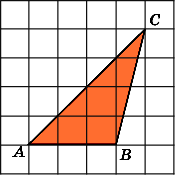
3.
Найдите площадь треугольника ABC,
считая стороны квадратных клеток
равными 1.

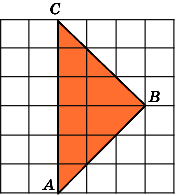
4.
Найдите площадь треугольника ABC,
считая стороны квадратных клеток
равными 1.

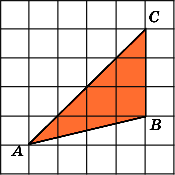
5.
Найдите площадь треугольника ABC,
считая стороны квадратных клеток
равными 1.

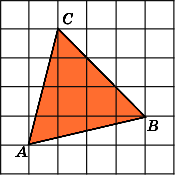
6.
Найдите площадь треугольника ABC,
считая стороны квадратных клеток
равными 1.

7.
Найдите площадь треугольника ABC,
считая стороны квадратных клеток
равными 1.

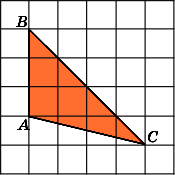
8.
Найдите площадь треугольника ABC,
считая стороны квадратных клеток
равными 1.

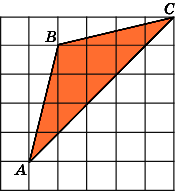
2. Площадь
прямоугольника, квадрата, параллелограмма,
ромба

1.
Найдите площадь параллелограмма ABCD,
считая стороны квадратных клеток
равными 1.

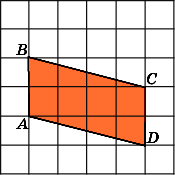
2.
Найдите площадь параллелограмма ABCD,
считая стороны квадратных клеток
равными 1.

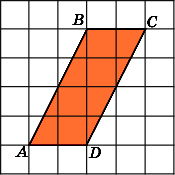
3.
Найдите площадь квадрата ABCD,
считая стороны квадратных клеток
равными 1.

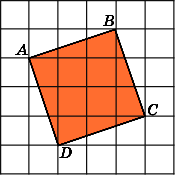
4.
Найдите площадь прямоугольника ABCD,
считая стороны квадратных клеток
равными 1.

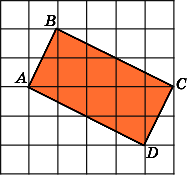
5.
Найдите площадь квадрата ABCD,
считая стороны квадратных клеток
равными 1.

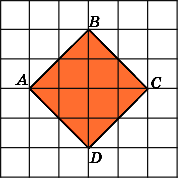
6.
Найдите площадь ромба ABCD,
считая стороны квадратных клеток
равными 1.

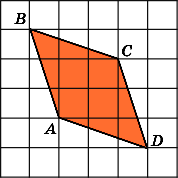
7.
Найдите площадь параллелограмма ABCD,
считая стороны квадратных клеток
равными 1.

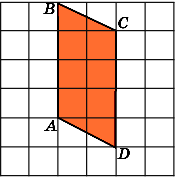
8.
Найдите площадь параллелограмма ABCD,
считая стороны квадратных клеток
равными 1.

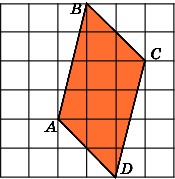
3.
Площадь трапеции

1.
Найдите площадь трапеции ABCD,
считая стороны квадратных клеток
равными 1.

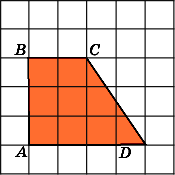
2.
Найдите площадь трапеции ABCD,
считая стороны квадратных клеток
равными 1.

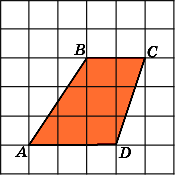
3.
Найдите площадь трапеции ABCD,
считая стороны квадратных клеток
равными 1.

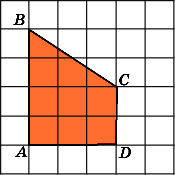
4.
Найдите площадь трапеции ABCD,
считая стороны квадратных клеток
равными 1.

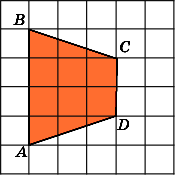
5.
Найдите площадь трапеции ABCD,
считая стороны квадратных клеток
равными 1.

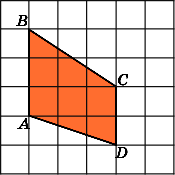
6.
Найдите площадь трапеции ABCD,
считая стороны квадратных клеток
равными 1.

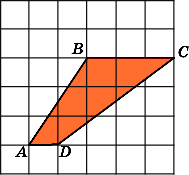
7.
Найдите площадь трапеции ABCD,
считая стороны квадратных клеток
равными 1.

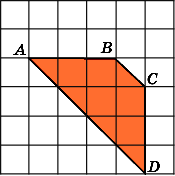
8.
Найдите площадь трапеции ABCD,
считая стороны квадратных клеток
равными 1.

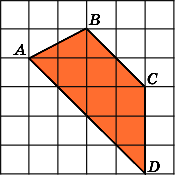
4.
Площадь выпуклых и невыпуклых
четырехугольников

1.
Найдите площадь четырехугольника ABCD,
считая стороны квадратных клеток
равными 1.

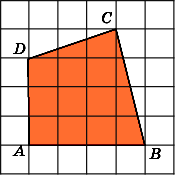
2.
Найдите площадь четырехугольника ABCD,
считая стороны квадратных клеток
равными 1.

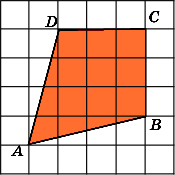
3.
Найдите площадь четырехугольника ABCD,
считая стороны квадратных клеток
равными 1.

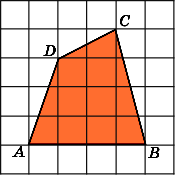
4.
Найдите площадь четырехугольника ABCD,
считая стороны квадратных клеток
равными 1.

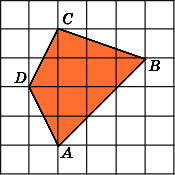
5.
Найдите площадь четырехугольника ABCD,
считая стороны квадратных клеток
равными 1.

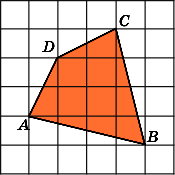
6.
Найдите площадь четырехугольника ABCD,
считая стороны квадратных клеток
равными 1.

7.
Найдите площадь четырехугольника ABCD,
считая стороны квадратных клеток
равными 1.

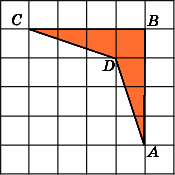
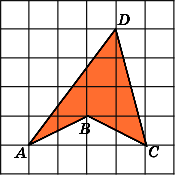
8.
Найдите площадь четырехугольника ABCD,
считая стороны квадратных клеток
равными 1.

5.
Площадь круга и его частей

1.
Найдите площадь S
сектора,
считая стороны квадратных клеток
равными 1. В ответе укажите .

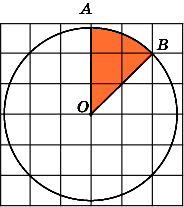
2.
Найдите площадь S
сектора,
считая стороны квадратных клеток
равными 1. В ответе укажите .

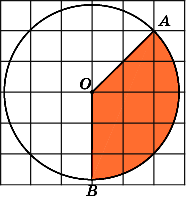
3.
Найдите площадь S
сектора,
считая стороны квадратных клеток
равными 1. В ответе укажите .

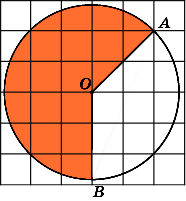
4.
Найдите площадь S
сектора,
считая стороны квадратных клеток
равными 1. В ответе укажите.

5.
Найдите площадь S
сектора,
считая стороны квадратных клеток
равными 1. В ответе укажите .

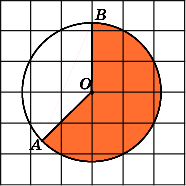
6.
Найдите площадь S
сектора,
считая стороны квадратных клеток
равными 1. В ответе укажите .

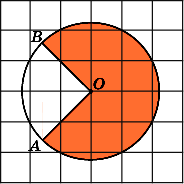
7.
Найдите площадь S
кольца,
считая стороны квадратных клеток
равными 1. В ответе укажите.

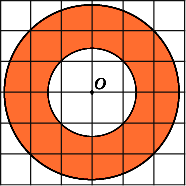
8.
Найдите площадь S
кольца,
считая стороны квадратных клеток
равными 1. В ответе укажите .

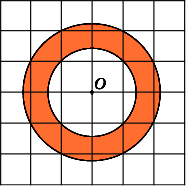
6.
Площадь фигур на координатной плоскости

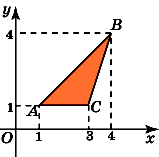
1.Найдите площадь треугольника, вершины
которого имеют координаты (1, 1), (4, 4), (3,
1).

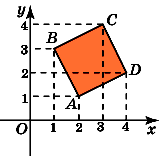
2.Найдите площадь квадрата, вершины
которого имеют координаты (2, 1), (1, 3), (3,
4), (4, 2).

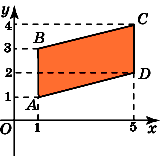
3.Найдите площадь параллелограмма,
вершины которого имеют координаты (1,
1), (1, 3), (5, 4), (5, 2).

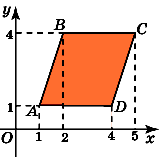
4.Найдите площадь параллелограмма,
вершины которого имеют координаты (1,
1), (2, 4), (5, 4), (4, 1).

5.Найдите площадь трапеции, вершины
которой имеют координаты (1, 1), (2, 4), (4,
4), (5, 1).

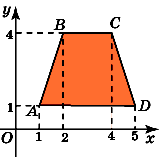
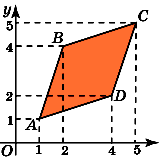
6.Найдите площадь ромба, вершины которого
имеют координаты (1, 1), (2, 4), (5, 5), (4, 2).

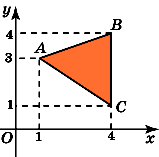
7.Найдите площадь треугольника, вершины
которого имеют координаты (1, 3), (4, 4), (4,
1).

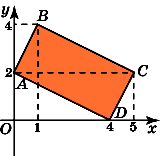
8.Найдите площадь прямоугольника, вершины
которого имеют координаты (0, 2), (1, 4), (5,
2), (4, 0).

Самостоятельная работа 1

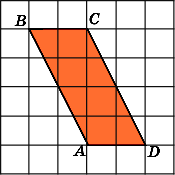
1.Найдите площадь параллелограммаABCD,
считая стороны квадратных клеток
равными 1.

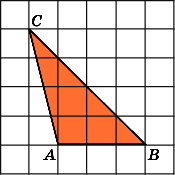
2.Найдите площадь треугольникаABC,
считая стороны квадратных клеток
равными 1.

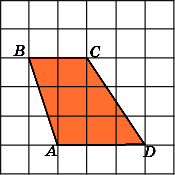
3.Найдите площадь трапецииABCD,
считая стороны квадратных клеток
равными 1.

4.Найдите площадь четырехугольникаABCD,
считая стороны квадратных клеток
равными 1.

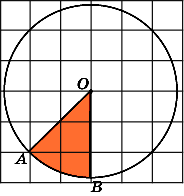
5.Найдите площадьS
сектора, считая стороны квадратных
клеток равными 1. В ответе укажите.

6.
Найдите площадь треугольника, вершины
которого имеют координаты

(1,
1), (1, 4), (4, 3).

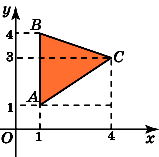
Самостоятельная работа 2

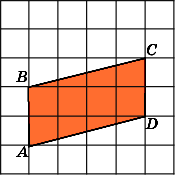
1.
Найдите площадь параллелограммаABCD, считая стороны
квадратных клеток равными 1.

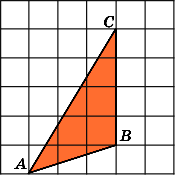
2.
Найдите площадь треугольникаABC,
считая стороны квадратных клеток
равными 1.

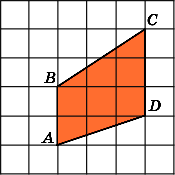
3.
Найдите площадь трапецииABCD,
считая стороны квадратных клеток
равными 1.

4.Найдите площадь четырехугольникаABCD,
считая стороны квадратных клеток
равными 1.

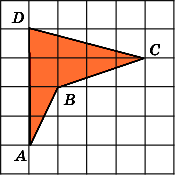
5.Найдите площадьS
сектора, считая стороны квадратных
клеток равными 1. В ответе укажите.

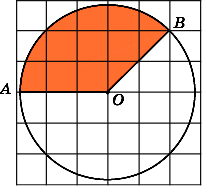
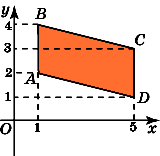
6.
Найдите площадь параллелограмма,
вершины которого имеют координаты (1,
2), (1, 4), (5, 3), (5, 1).

Самостоятельная работа 3

1.
Найдите площадь квадратаABCD,
считая стороны квадратных клеток
равными 1.

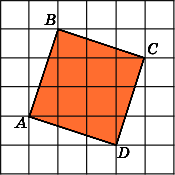
2.Найдите площадь треугольникаABC,
считая стороны квадратных клеток
равными 1.

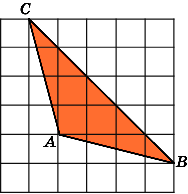
3.Найдите площадь трапецииABCD,
считая стороны квадратных клеток
равными 1.

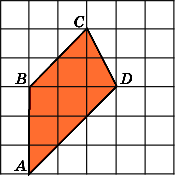
4.Найдите площадь четырехугольникаABCD,
считая стороны квадратных клеток
равными 1.

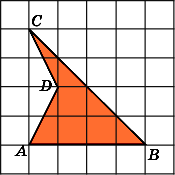
4.
Найдите площадьS
кольца, считая стороны квадратных
клеток равными 1. В ответе укажите.

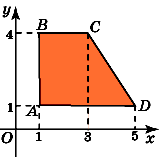
6.
Найдите площадь трапеции, вершины
которой имеют координаты

(1,
1), (1, 4), (3, 4), (5, 1).

ОТВЕТЫ

Задания
для тренировки.

1.
Площадь треугольника

1.
8.2.6.3.9.4. 6.5.7,5.6.8.7.6.8. 7,5.

2.
Площадь прямоугольника, квадрата,
параллелограмма, ромба

1.8.2.8.3.10.4. 10.5.8.6.8.7.8.8. 10.

3.
Площадь трапеции

1.92.7,5.3.9.4. 9.5.7,5.6.6.7.7,5.8. 9.

4.
Площадь выпуклых и невыпуклых
четырехугольников

1.12,5.2.12.3.10,5.4. 8.5.9.6.4.7.4.8. 6.

5.
Площадь круга и его частей

1.2.2.1.3.3.4. 5.5.3,125.6.3,75.7.6.8. 3.

6.
Площадь фигур на координатной плоскости

1.3.2.5.3.8.4. 9.5.9.6.8.7.4,5.8. 10.

Самостоятельные
работы

Самостоятельная
работа 1

1.
8. 2.6.3.7,5.4.8.5. 1.6.4,5.

Самостоятельная
работа 2

1.
8. 2.6.3.7,5.4.5,5.5. 3.6.
8.

Самостоятельная
работа 3

1.
10. 2.7,5.3.7,5.4.6.5. 4.6.
9.

Источник

Вычисление площадей фигур в различных системах координат

Площадь плоской фигуры в декартовых координатах

Площадь фигуры, ограниченной кривой, заданной параметрически

Площадь фигуры, заданной в полярных координатах

Площадь фигуры по координатам вершин

Санкт-Петербургский

Примеры решения задач.

6. Найдите площадь трапеции abcd, считая стороны квадратных клеток равными 1.

Задания для тренировки.

Самостоятельная работа 1

Самостоятельная работа 2

Самостоятельная работа 3

Вам также может понравиться

Как быстро найти работу в екатеринбурге

Как найти работу на своем манипуляторе

Как найти сердечный выброс

Добавить комментарий Отменить ответ