Как найти площадь трапеции огэ 2022

Как найти площадь трапеции огэ 2022

Каталог заданий.
Трапеция


Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

1

Тип 17 № 39

i

Найдите площадь трапеции, изображённой на рисунке.

Аналоги к заданию № 39: 117 143 311682 … Все

Источник: Де­мон­стра­ци­он­ная вер­сия ГИА—2013 по ма­те­ма­ти­ке

Решение

·

Помощь

2

Тип 17 № 117

i

Найдите площадь трапеции, изображённой на рисунке.

Аналоги к заданию № 39: 117 143 311682 … Все

Источник: ГИА по ма­те­ма­ти­ке 28.05.2013. Ос­нов­ная волна. Ва­ри­ант 1309

Решение

·

Помощь

3

Тип 17 № 143

i

Найдите площадь трапеции, изображённой на рисунке.

Аналоги к заданию № 39: 117 143 311682 … Все

Источник: ГИА по ма­те­ма­ти­ке 28.05.2013. Ос­нов­ная волна. Ва­ри­ант 1313

Решение

·

Помощь

4

Тип 17 № 169881

i

Основания трапеции равны 18 и 12, одна из боковых сторон равна 4 корень из: начало аргумента: 2 конец аргумента , а угол между ней и одним из оснований равен 135°. Найдите площадь трапеции.

Аналоги к заданию № 169881: 339837 169882 348664 … Все

Решение

·

Помощь

5

Тип 17 № 169883

i

Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а синус угла между ней и одним из оснований равен дробь: числитель: 1, знаменатель: 3 конец дроби . Найдите площадь трапеции.

Аналоги к заданию № 169883: 169884 169885 324155 … Все

Решение

·

Помощь

Пройти тестирование по этим заданиям

Источник
Решаем 23 задание из ОГЭ по математике

Всем привет. Рада тому, что вы меня читаете и комментируете

Сегодня разбираем геометрическую задачу из второй части ОГЭ. Задание из свежего варианта Ларина.

Вот условие задачи

​

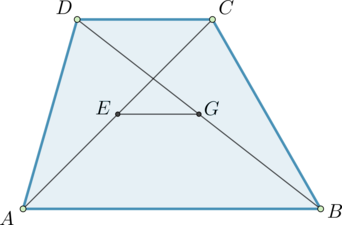
Диагонали  AC и BD трапеции  ABCD   пересекаются  в  точке O. Площади  треугольников  AOD и BOC равны  соответственно 25 и 16.​

​Найдите  площадь  трапеции​

Чтобы решить эту задачу надо знать свойства подобия и свойства площадей, одно из которых надо потребуется в ходе решения

Для начала я увидела, что треугольники АOD и BOC подобны и по свойству подобия отношение площадей этих треугольников будет равно квадрату коэффициента подобия, отсюда найдем сам коэффициент.

Решаем 23 задание из ОГЭ по математике
Решаем 23 задание из ОГЭ по математике

Далее, вспоминаем, что

Если два треугольника имеют одинаковые высоты, то отношение их площадей равно отношению длин оснований (сторон, на которые опущены эти высоты).

Решаем 23 задание из ОГЭ по математике

Теперь можно легко найти площадь трапеции

Решаем 23 задание из ОГЭ по математике

Спасибо за внимание

Буду рада вашим лайкам, комментариям, а также вашей подписке

Также приглашаю в свои группы в Телеграм и Вконтакте

До новых встреч на канале Простаяматематика.рф

#геометрия

#решимзадачу

#интереснаязадача

#огэпоматематике

#блогрепетитора

Источник

Рассмотрим несколько задач.

#1 #2 #3 #4 #5

Задача #1

(Номер задачи на fipi.ru — B11571). На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Трапеция

Прежде чем приступать к решению задачи, вспомним теорию >>

Трапеция — четырёхугольник, две стороны которой параллелльны, а две другие нет. Параллельные стороны называются основаниями, а непаралельные — боковыми.

Площадь трапеции вычисляется по формуле:

    [S=frac{a+b}{2}cdot h]

где a и b — основания трапеции, h — высота трапеции.

Решение:
Посмотрим на рисунок. Из него видно, что основания трапеции равны соответственно: a = 2, b = 6. Из рисунка также находим высоту трапеции: h = 7.

Таким образом, осталось подставить все найденный значения в формулу и найти площадь трапеции:

    [S=frac{2+6}{2}cdot 7 = 28]

Ответ: площадь трапеции равна: 28 ед. кв.

Задача #2

(Номер задачи на fipi.ru — E46263). На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Трапеция площадью 36

Решение:
Посмотрим на рисунок. Из него видно, что основания трапеции равны соответственно: a = 4, b = 8. Из рисунка также находим высоту трапеции: h = 6.

Таким образом, осталось подставить все найденный значения в формулу и найти площадь трапеции:

    [S=frac{4+8}{2}cdot 6 = 36]

Ответ: площадь трапеции равна: 36 ед. кв.

Задача #3

(Номер задачи на fipi.ru — 283DE4). На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Трапеция площадью 12

Решение:
Посмотрим на рисунок. Из него видно, что основания трапеции равны соответственно: a = 2, b = 6. Из рисунка также находим высоту трапеции: h = 3.

Таким образом, осталось подставить все найденный значения в формулу и найти площадь трапеции:

    [S=frac{2+6}{2}cdot 3 = 12]

Ответ: площадь трапеции равна: 12 ед. кв.

Задача #4

(Номер задачи на fipi.ru — 383C46). На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Трапеция площадью 10

Решение:
Посмотрим на рисунок. Из него видно, что основания трапеции равны соответственно: a = 3, b = 7. Из рисунка также находим высоту трапеции: h = 2.

Таким образом, осталось подставить все найденный значения в формулу и найти площадь трапеции:

    [S=frac{3+7}{2}cdot 2 = 10]

Ответ: площадь трапеции равна: 10 ед. кв.

Задача #5

(Номер задачи на fipi.ru — 2E7B84). На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Трапеция площадью 30

Решение:
Посмотрим на рисунок. Из него видно, что основания трапеции равны соответственно: a = 3, b = 7. Из рисунка также находим высоту трапеции: h = 6.

Таким образом, осталось подставить все найденный значения в формулу и найти площадь трапеции:

    [S=frac{3+7}{2}cdot 6 = 30]

Ответ: площадь трапеции равна: 30 ед. кв.

Источник

18. Площади геометрических фигур


1. Вспоминай формулы по каждой теме


2. Решай новые задачи каждый день


3. Вдумчиво разбирай решения

Площадь трапеции

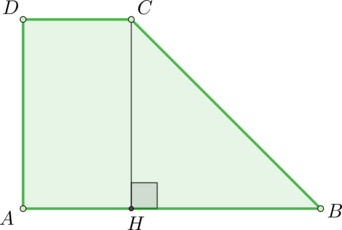
Найдите площадь прямоугольной трапеции, основания которой равны (6) и (2), большая боковая сторона составляет с основанием угол (45^circ).

Проведем высоту (CH).

Так как (angle HBC=45^circ), то (angle HCB=45^circ). Следовательно, (triangle HBC) равнобедренный и (HB=HC).
(ADCH) – прямоугольник, следовательно, (AH=DC=2). Тогда (CH=HB=6-2=4). Тогда площадь трапеции равна [S=dfrac{AB+DC}2cdot CH=dfrac{2+6}2cdot 4=16]

Ответ: 16

Основания прямоугольной трапеции равны (12) и (4). Ее площадь равна (64). Найдите острый угол этой трапеции. Ответ дайте в градусах.

Проведем высоту (CH).

(ADCH) – прямоугольник, следовательно, (AH=DC=4). Тогда (HB=12-4=8). Площадь трапеции равна [64=dfrac{AB+DC}2cdot CH=dfrac{4+12}2cdot CHquadRightarrowquad
CH=8] Заметим, что мы получили, что (CH=HB=8). То есть (triangle
CHB) равнобедренный, значит, углы при основании равны, то есть (angle HCB=angle HBC). Так как сумма острых углов в прямоугольном треугольнике равна (90^circ), то (angle B=angle
HBC=90^circ:2=45^circ).

Ответ: 45

Основания трапеции равны (18) и (6), боковая сторона, равная (7), образует с одним из оснований угол (150^circ). Найдите площадь трапеции.

Пусть (AD=7), тогда (angle ADC=150^circ). По свойству трапеции (angle DAB=180^circ-150^circ=30^circ). Проведем (DHperp
AB).

Рассмотрим (triangle ADH). Катет, лежащий против угла (30^circ), равен половине гипотенузы, следовательно, (DH=AD:2=3,5). Тогда площадь трапеции равна [S=dfrac{AB+DC}2cdot DH=dfrac{18+6}2cdot 3,5=42]

Ответ: 42

Основания трапеции равны (27) и (9), боковая сторона равна (8). Площадь трапеции равна (72). Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ дайте в градусах.

Пусть (AD=8). Проведем (DHperp AB).

Тогда площадь трапеции равна [72=dfrac{AB+DC}2cdot DH=dfrac{27+9}2cdot DHquadRightarrowquad
DH=4] Рассмотрим прямоугольный (triangle ADH). Так как катет (DH) равен половине гипотенузы (AD), то угол (DAH) равен (30^circ).

Ответ: 30

Основания равнобедренной трапеции равны (14) и (26), а ее боковые стороны равны (10). Найдите площадь трапеции.

Проведем высоту (BH). По свойству равнобедренной трапеции (AH=(AD-BC):2=(26-14):2=6).

Тогда из прямоугольного треугольника (ABH): [BH=sqrt{AB^2-AH^2}=sqrt{10^2-6^2}=8] Тогда площадь трапеции: [S=dfrac{AD+BC}2cdot BH=dfrac{26+14}2cdot 8=160]

Ответ: 160

Основания равнобедренной трапеции равны (7) и (13), а ее площадь равна (40). Найдите боковую сторону трапеции.

Проведем высоту (BH).

Площадь трапеции равна [40=dfrac{AD+BC}2cdot BH=dfrac{7+13}2cdot BHquadRightarrowquad BH=
4] Рассмотрим прямоугольный (triangle ABH). По свойству равнобедренной трапеции (AH=(AD-BC):2=(13-7):2=3). Следовательно, [AB=sqrt{AH^2+BH^2}=5]

Ответ: 5

Основания равнобедренной трапеции равны (14) и (26), а ее периметр равен (60). Найдите площадь трапеции.

Проведем высоту (BH). По свойству равнобедренной трапеции (AH=(AD-BC):2=(26-14):2=6).

Так как периметр трапеции равен (60), а боковые стороны равны, то [AB=dfrac{60-14-26}2=10] Тогда из прямоугольного треугольника (ABH): [BH=sqrt{AB^2-AH^2}=sqrt{10^2-6^2}=8] Тогда площадь трапеции: [S=dfrac{AD+BC}2cdot BH=dfrac{26+14}2cdot 8=160]

Ответ: 160

УСТАЛ? Просто отдохни

Источник

Рассмотрим разновидность задания № (23) — геометрическая задача на вычисление площади трапеции.

Для выполнения необходимо вспомнить теорию.

Пример:

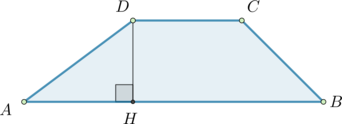
известно, что периметр равнобедренной трапеции с основаниями 10 и 58 равен 128. Найди площадь трапеции.

Как решить задание из примера?

Для получения максимального балла задание нужно оформлять разборчивым почерком с подробным решением. Обязательно должны присутствовать чертёж, дано и решение.

э 1 3.png

Рис. (1). Чертёж

Дано:

ABCD

 — трапеция;

AB=CD

;

PABCD=128

;

BC=10

;

AD=58

.

Решение:

для решения данной задачи будем использовать формулу площади трапеции

P=AB+CD+BC+AD=2⋅AB+BC+AD

 (поскольку периметр — это сумма длин всех сторон, и трапеция равнобедренная).

Подставим в данное выражение значения периметра и сторон:

(AB=) 30.

Так как трапеция равнобедренная, то

AH=(AD
−BC)2=(58
−10)2=24.

Найдём (BH). По теореме Пифагора имеем:

BH=AB2−AH2=302
−242=18.

Так как узнали все компоненты, то найдём площадь:

S=BC+AD2⋅BH=(10+58)2
·18=612.

Ответ: 612.

Источники:

Рис. 1. Чертёж. © ЯКласс.

Источник

Добавить комментарий