Прямоугольная трапеция является трапецией, у которой одна из боковых сторон перпендикулярна основаниям. Средняя линия прямоугольной трапеции равна половине суммы ее оснований. (рис.105.1)
m=(b+d)/2
Высота прямоугольной трапеции равна ее боковой стороне-перпендикуляру. Следовательно, площадь трапеции, которая обычно равна произведению высоты на среднюю линию, преобразуется в произведение боковой стороны на среднюю линию. (рис.105.2)
S=hm=am=(a(b+d))/2
Вторая боковая сторона прямоугольной трапеции, находящаяся под углом к основаниям, отличным от 90 градусов, вычисляется по теореме Пифагора в прямоугольном треугольнике с высотой.
c=√(h^2+〖(d-b)〗^2 )=√(a^2+〖(d-b)〗^2 )
Периметр такой трапеции вычисляется также как обычной, сложением всех ее сторон.
P=a+b+c+d=a+b+d+√(a^2+〖(d-b)〗^2 )
Обе диагонали прямоугольной трапеции являются гипотенузами в прямоугольных треугольниках со стороной, перпендикулярной основаниям. Поэтому вычислить их становится возможным, используя теорему Пифагора. (рис.105.3)
d_1=√(a^2+b^2 )
d_2=√(a^2+d^2 )
Если боковые стороны прямоугольной трапеции в сумме дают то же, что и основания, то внутри такой трапеции можно вписать окружность. Радиусом вписанной окружности будет служить половина высоты или, в данном случае, половина квадратного корня из произведения оснований.
r=√bc/2
Вокруг прямоугольной трапеции нельзя описать окружность, для этого она должна стать либо равнобокой трапецией, либо прямоугольником
Укажите размеры:
Основание 1
Основание 2
Боковая сторона (прямая)
Результат:
Решение:
Ссылка на страницу с результатом:
# Теория
Трапеция – это четырёхугольник у которого две противоположные стороны параллельны и не равны между собой. Параллельные стороны трапеции называются основаниями, а две другие стороны называются боковыми.
Основания трапеции – это две параллельные противоположные стороны.
Высота трапеции – это прямой отрезок проведённый от центра до границы круга. В прямоугольной трапеции высота равна боковой стороне с прямым углом.
Бывают прямоугольная, равнобедренная и неравнобедренная трапеции.
Формула площади трапеции
Чтобы посчитать площадь прямоугольной трапеции, необходимо знать размеры её оснований и боковой стороны с прямым углом.
Площадь прямоугольной трапеции расчитывается по формуле:
a
b
h
S = dfrac{a + b}{2} cdot h
- S – площадь трапеции
- a – основание трапиции
- b – основание трапеции
- h – боковая сторона с прямым углом
Похожие калькуляторы:
Войдите чтобы писать комментарии
Площадь прямоугольной трапеции: онлайн калькулятор, формула расчета, пример вычисления
Сергей Феликсович Савельев
Эксперт по предмету «Калькуляторы»
Задать вопрос автору статьи
Ниже вы узнаете, как выглядят формулы для нахождения площади прямоугольной трапеции, а также сможете воспользоваться онлайн-калькуляторами для её расчёта.
Определение 1
Особенность прямоугольной трапеции в том, что её высота равна стороне, расположенной перпендикулярно двум основаниям.
Для того чтобы вычислить площадь прямоугольной трапеции через 3 её стороны, воспользуйтесь нашим онлайн-калькулятором. Для расчёта введите имеющиеся данные в поля для ввода.
Площадь прямоугольной трапеции

Высота прямоугольной трапеции $h$ равна длине стороны $c$, расположенной под прямым углом к двум основаниям трапеции $a$ и $c$.
Следовательно, формула для вычисления площади прямоугольной трапеции имеет вид:
$S = frac12 cdot (a + c) cdot b$, где
$a$ — малое основание;
$с$ — большее основание;
$b$ — перпендикулярная основаниям сторона.
Пример 1
Задача
Дана прямоугольная трапеция, сторона $b$ у которой равна $2.32$ см, сторона $a$ составляет $2.42$, и сторона $c$ равна $3.94$ см. Чему равна площадь трапеции?
Решение:
Воспользуемся приведённой выше формулой:
$S =frac{(2.42 + 3.93) cdot 2.32}{2} = 7.37$ кв. см.
Проверим ответ с помощью онлайн-калькулятора. Значения совпадают, а значит, решение найдено верно.
Также площадь прямоугольной трапеции можно рассчитать и по другим формулам, общим для всех видов трапеций, например, через среднюю линию и высоту. Высоту в формуле также можно заменить на сторону, перпендикулярную основаниям.
Площадь трапеции по высоте и средней линии

Формула нахождения площади трапеции по высоте и средней линии:
$S = m cdot h$, где
$S$ – площадь трапеции,
$m$ – средняя линия,
$h$ – высота трапеции.
Другой способ расчёта площади прямоугольной трапеции — через длины оснований и два угла, расположенных при одном основании.
Площадь трапеции через ее основание и углы

Формула нахождения площади трапеции через ее основание и углы при основании:
$S = frac12 cdot (b^2 – g^2) cdot frac{sin (α) cdot sin (γ)}{sin (α + γ)}$, где
$S$ – площадь трапеции,
$b$ – большее основание,
$g$ – малое основание,
$α$ – первый угол при основании,
$γ$ – второй угол при основании.
Также площадь прямоугольной трапеции можно найти через диагонали и угол между ними.
Площадь трапеции по диагонали и углу между диагоналями

Формула нахождения площади трапеции по диагонали и углу между диагоналями:
$S =frac12 cdot d1 cdot d2 cdot sin (α)$, где
$S$ – площадь трапеции,
$d1$ – первая диагональ,
$d2$ – вторая диагональ,
$α$ – угол между диагоналями.
Рассмотрим пример.
Пример 2
Задача
Дана прямоугольная трапеция с диагоналями $d1$ и $d2$, равными $2.22$ см и $2.64$ см. Угол между диагоналями $α$ равен $56°$. Чему равна площадь прямоугольной трапеции?
Решение:
Синус заданного угла $α$ равен $0.83$, найти его можно по специальным таблицам, приведённым на нашем сайте. Теперь подставим все известные значения:
$S = frac{2.22 cdot 2.64 cdot 0.83}{2} = 2.43$ кв. см.
Вычисленный ответ совпадает с ответом онлайн-калькулятора, а значит, решение — верное.
И наконец, рассмотрим случай когда нет данных о том, какие стороны являются основаниями, а какая сторона расположена под прямым углом, но при этом известны все стороны трапеции.
Площадь трапеции по четырём сторонам

Формула нахождения площади трапеции по четырём сторонам выглядит следующим образом:
$S = frac{a + b}{2} cdot sqrt{c^2 – (frac{(b – a)^2 + c^2 – d^2}{2 cdot (b – a)})^2}$, где
$S$ – площадь трапеции,
$a$ – малое основание,
$b$ – большее основание,
$c, d$ – боковые стороны.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата написания статьи: 26.06.2019
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
🤔 Что это за калькулятор?
Калькулятор площади трапеции — это веб-инструмент, который помогает рассчитать площадь трапеции на основе ее размеров, которые вводит пользователь. Обычно пользователю нужно указать длины двух параллельных сторон трапеции (оснований) и ее высоту.
Калькулятор площади трапеции может быть полезен при решении задач геометрии, в которых необходимо быстро вычислить площадь трапеции. Также он может использоваться при расчетах материалов для строительства и дизайна, где требуется знание площади поверхности трапеции.
🧮 Как работает калькулятор и какие есть примеры использования?
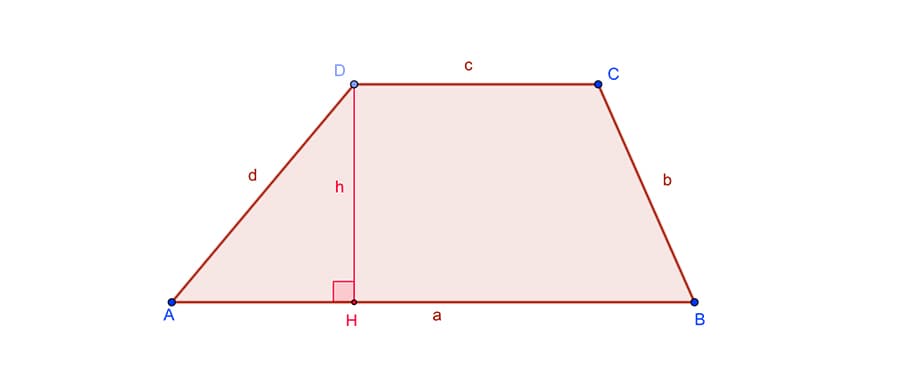
Работа калькулятора площади трапеции основана на формуле, которая используется для расчета площади трапеции. Формула для расчета площади трапеции выглядит следующим образом:
S = (a + b) * h / 2
Где “a” и “b” — это длины оснований трапеции, а “h” – ее высота.
Чтобы использовать калькулятор, пользователь должен ввести длины двух оснований трапеции и ее высоту в соответствующие поля веб-интерфейса калькулятора. После того, как пользователь ввел данные, калькулятор автоматически рассчитывает площадь трапеции и отображает результат на экране.
Пример
Разберем пример использования калькулятора на реальном объекте
Допустим, вы планируете купить ковер для своей гостиной комнаты, и вам нужно знать, какой размер ковра нужен. Ваша гостиная имеет форму трапеции, и вы не знаете, как рассчитать размер ковра, чтобы он идеально соответствовал форме комнаты.
В этом случае вы можете использовать калькулятор площади трапеции для определения площади поверхности пола в гостиной и, следовательно, определения размера ковра, который вам нужен.
Для этого вам необходимо измерить длины двух параллельных сторон комнаты (оснований) и ее высоту. Например, пусть одно основание комнаты равно 6 метров, а другое – 8 метров, а высота составляет 4 метра.
Вводим эти значения в соответствующие поля калькулятора площади трапеции, и получаем результат – площадь гостиной равна 28 квадратных метров.
Теперь вы можете использовать эту информацию, чтобы определить размер ковра, который вам нужен. Например, если вы решили приобрести ковер, покрывающий всю площадь комнаты, то вам понадобится ковер размером, равным 28 квадратных метров.
Также примеры использования калькулятора площади трапеции могут включать следующее:
- Расчет площади трапеции в задачах геометрии на уроках в школе или вузе.
- Расчет площади поверхности трапеции при планировании строительства, например, для расчета необходимого количества материалов.
- Использование калькулятора при разработке дизайна или макетов, когда нужно знать площадь поверхности трапеции для правильного распределения элементов.
- Расчет площади трапеции в повседневной жизни, например, при расчете площади участка земли или для определения площади поверхности торта или пиццы.
Какие виды трапеций существуют
Существует несколько видов трапеций, которые отличаются формой и свойствами сторон и углов. Вот некоторые из них:
- Прямоугольная трапеция — это трапеция, у которой одно основание перпендикулярно к высоте. Углы между боковыми сторонами и основаниями равны по два, как и у прямоугольника.
- Равнобокая трапеция — это трапеция, у которой боковые стороны равны друг другу. Углы между боковыми сторонами и основаниями не равны.
- Равнобедренная трапеция — это трапеция, у которой две боковые стороны и углы между ними равны. Другие две стороны не являются равными и не равны углам между боковыми сторонами и основаниями.
- Криволинейная трапеция — это трапеция, у которой боковые стороны не параллельны друг другу и имеют форму кривых линий.
- Изогнутая трапеция — это трапеция, у которой одно или оба основания имеют изогнутую форму, но боковые стороны все еще параллельны.
Каждый вид трапеции имеет свои уникальные свойства, что делает их полезными в различных математических и геометрических задачах.
Площадь каких видов трапеций может рассчитать наш калькулятор?
Калькулятор площади трапеции может рассчитать площадь всех видов трапеций, включая прямоугольную, равнобокую, равнобедренную, криволинейную и изогнутую трапеции. Для расчета площади трапеции необходимо знать длины ее оснований и высоту. Если речь идет о криволинейной трапеции или изогнутой трапеции, то также необходимо знать длины наклонных боковых сторон.
Калькулятор площади трапеции учитывает все эти параметры и автоматически рассчитывает площадь трапеции, когда вы вводите соответствующие значения в поля веб-интерфейса калькулятора.
❓Вопросы и ответы
При расчете площади трапеции могут возникать различные вопросы. Вот некоторые из наиболее частых вопросов и ответы на них:
Как найти высоту трапеции, если она неизвестна?
Высота трапеции является перпендикулярной линией, проведенной от одного основания до другого. Если вы не знаете высоту, но знаете длины оснований и площадь трапеции, то можно использовать формулу S = (a + b)h/2, где S – площадь, a и b – длины оснований, h – высота. Решая эту формулу относительно h, вы получите высоту трапеции: h = 2S / (a + b).
Как рассчитать площадь криволинейной трапеции?
Чтобы рассчитать площадь криволинейной трапеции, необходимо знать длины ее оснований и наклонных боковых сторон, а также высоту. Затем вы можете использовать формулу для площади трапеции: S = (a + b)h/2, где a и b – длины оснований, h – высота. Для криволинейной трапеции вместо a и b необходимо использовать длины соответствующих наклонных сторон.
Как проверить, что я правильно рассчитал площадь трапеции?
Вы можете проверить правильность своих расчетов, используя формулу для площади трапеции. Также вы можете использовать наш онлайн калькулятор площади трапеции, чтобы проверить свои расчеты. Если вы измерили длины сторон и углы трапеции с помощью инструментов, то также можете проверить свои измерения, сравнив их с теоретическими значениями.
Можно ли рассчитать площадь трапеции, зная только диагонали?
Если вы знаете длины диагоналей трапеции и угол между ними, то можно использовать формулу для расчета площади трапеции: S = (1/2)d1d2sin(theta), где d1 и d2 – диагонали, а theta – угол между ними.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
- Калькулятор длины дуги. Рассчитайте онлайн длину дуги окружности по радиусу и углу или по формуле Гюйгенса.
- Калькулятор объема трубы. Рассчитайте онлайн объем трубы в куб. м. или литрах в зависимости от диаметра и длины трубопровода.
- Калькулятор объема пирамиды. Рассчитайте объем пирамиды по высоте, площади основания или стороне основания. Основание может быть любой формы.
- Калькулятор объема и площади усеченного конуса. Рассчитайте онлайн объем и площадь поверхности усеченного конуса по его радиусам и высоте.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Как рассчитать площадь трапеции
На данной странице калькулятор поможет рассчитать площадь трапеции онлайн. Для расчета задайте высоту и длуну основания трапеции.
Трапеция – четырёхугольник, у которого две стороны параллельны (основания трапеции), а две другие – непараллельны (боковые стороны трапеции). Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
Через основания и высоту
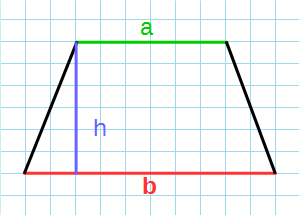
Формула для нахождения площади трапеции через основания и высоту:
a,b – основания трапеции; h – высота трапеции.
Через среднюю линию и высоту
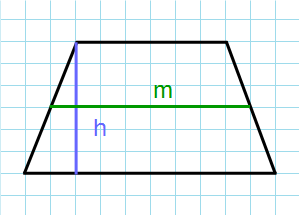
Формула для нахождения площади трапеции через основания и среднюю линию:
m – средняя линия; h – высота трапеции.
Через четыре стороны
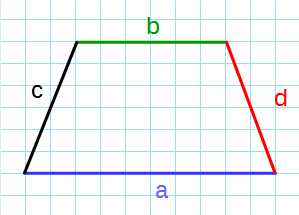
Формула для нахождения площади трапеции через основания и среднюю линию:
a – нижнее основание; b – верхнее основание; c, d – боковые стороны.
Через диагонали и угол между ними
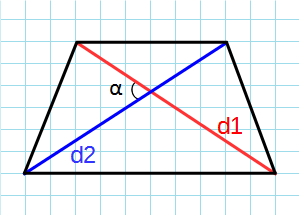
Формула для нахождения площади трапеции через диагонали и угол между ними:
d1, d2 – диагонали трапеции; α – угол между диагоналями.
Через среднюю линию, боковую сторону и угол при основаниии
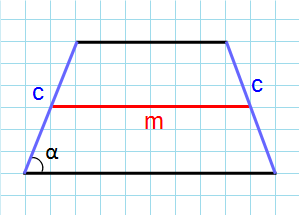
Формула для нахождения площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании:
m – средняя линия трапеции; c – боковая сторона трапеции; α – угол при основании.
Через радиус вписанной окружности
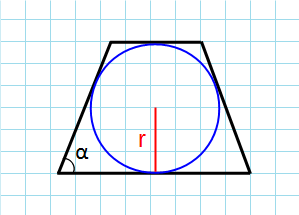
Формула для нахождения площади равнобедренной трапеции через радиус вписанной оккужности:
r – радиус окружности; α – угол при основании.
