Как найти площадь трапеции равна прямоугольной

Как найти площадь трапеции равна прямоугольной

Прямоугольная трапеция особенна тем, что имеет сторону, перпендикулярную двум неравным основаниям фигуры. Важным признаком является и наличие двух прямых смежных углов. Поиск площади прямоугольной трапеции возможен по любой из общих формул, предназначенных для данного вычисления любых трапеций (прямоугольной, равнобедренной, произвольной).

5 способов вычисления:

  1. через три стороны трапеции;
  2. умножив высоту трапеции на среднюю линию;
  3. через основание и углы;
  4. через диагонали и углы между ними;
  5. через четыре стороны.

Вычисление площади трапеции через три её стороны (основания и перпендикулярную сторону) подходит только для прямоугольных трапеций.

Площадь прямоугольной трапеции по трём сторонам

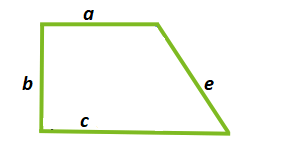
Значение высоты прямоугольной трапеции совпадает со значением её стороны, перпендикулярной основаниям фигуры. Площадь такой фигуры можно найти через три известных стороны.

Рисунок 1.

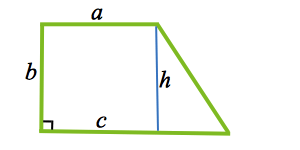
a – малое основание;

b – перпендикулярная сторона;

c – большое основание;

h – высота.

Рисунок 1. Прямоугольная трапеция. Высота h.

 [boldsymbol{S}=frac{mathbf{1}}{mathbf{2}} *(boldsymbol{a}+boldsymbol{c}) * boldsymbol{b}, text { где } mathbf{S}], где S – площадь прямоугольной трапеции.

Если половину суммы малого и большого основания умножить на перпендикулярную сторону трапеции или высоту, в результате получается площадь.

Задача.

Найдите площадь прямоугольной трапеции S, если малое основание a составляется 4,84 см, а большое с – 7,88 см, перпендикулярная основаниям высота b равна 4,64 см.

Решение:

Основываясь на данные о трёх её сторонах, по соответствующей формуле найдём площадь.

[boldsymbol{S}=frac{1}{2} *(4,84+7,88) * 4,64=mathbf{2 9}, mathbf{5 1} text { кв.см }]

Ответ: Площадь прямоугольной трапеции равна 29,51 кв.см.

Площадь прямоугольной трапеции по высоте и средней линии

Для расчета площади потребуются данные о высоте трапеции и линии, проведенной посередине фигуры. Произведение этих величин и составит площадь. Рассмотрим рисунок 2.

Рисунок 2.

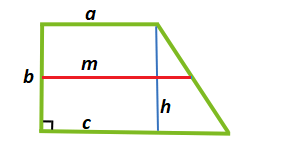
[boldsymbol{S}=boldsymbol{m} * boldsymbol{h}], где S – площадь фигуры, m – средняя линия, а h – высота, которую можно заменять на перпендикулярную основаниям сторонуb.

Задача.

Найдите площадь прямоугольной трапеции S, зная высоту h – 4,64 см и среднюю линию m – 6,36 см.

Решение:

Найдём площадь трапеции путём умножения известных величин.

[boldsymbol{S}=4,64 * 6,36=29,51 text { кв.см }]

Ответ: S = 29,51 кв.см.

Вычисление площади по основаниям и углам

Зная значения оснований трапеции и углов при них, для вычисления площади нужно половину разницы квадратов оснований фигуры умножить на частное из произведения синусов углов при основании и синуса суммы этих углов. Рассмотрим рисунок 3.

Рисунок 3.

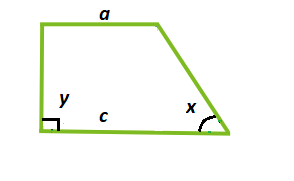
[S=frac{1}{2} *left(c^{2}-a^{2}right) * frac{sin (y) * sin (x)}{sin (y+x)}], где S – площадь; с – большое основание;a – малое основание;

y, x – первый и второй угол при основании.

Задача.

Как узнать площадь прямоугольной трапеции S по формуле оснований и углов, если малое снование a равно 4,84 см, а большое с – 7,88 см, первый угол при основании y прямой, а второй x равен 56,8о?

Решение:

Рассчитаем площадь трапеции, используя данные об основаниях и углах при большом основании.

[boldsymbol{S}=frac{1}{2} *left(7,88^{2}-4,84^{2}right) * frac{sin (90) * sin (56,8)}{sin (90+56,8)}=mathbf{2 9 , 4 8} mathbf{кв.см}]

Ответ: S = 29.48 кв.см.

Нет времени решать самому?

Наши эксперты помогут!

Площадь прямоугольной трапеции через диагонали и углы между ними

Умножив синус угла, образованный на пересечении диагоналей, на произведение диагоналей, делённое пополам, получим площадь прямоугольной трапеции.

Рисунок 4.

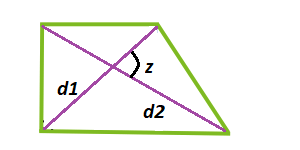
[S=frac{1}{2} * d 1 * d 2 * sin (x)], где S – площадь; d1 – диагональ 1; d2 – диагональ 2; z – угол между диагоналями.

Задача.

Найдите площадь прямоугольной трапеции, имя данные первой диагонали d1, второй – d2 и угла между ними z. d1 = 2,23 см; d2 = 2,65 см, z = 57o.

Решение:

Пользуясь формулой расчёта площади, при известных диагоналях и углу между ними, составим решение.

[boldsymbol{S}=frac{1}{2} * 2,23 * 2,65 * sin (57)=mathbf{2}, mathbf{4 8} mathbf { кв.см }]

Ответ: S=2,48 кв.см

Площадь прямоугольной трапеции, исходя из значения всех её сторон

Если известны показатели всех сторон прямоугольной трапеции, то вычислить её площадь можно по формуле, приведённой ниже.

[left.S=frac{a+c}{2} * sqrt{e^{2}-left(frac{(c-a)^{2}+e^{2}-b^{2}}{2 *(c-a)}right.}right)^{2}], где a – малое основание; c – большое основание; b – перпендикулярная основаниям сторона; e – неперпендикулярная боковая сторона.

Рисунок 5

Задача.

Дано: a = 3 см; b = 3 см; c = 5 см; e = 3,5 см.

Найти: площадь трапеции S.

Решение: применяя формулу расчёта площади по всем сторонам фигуры, найдём площадь трапеции.

[S=frac{3+5}{2} * sqrt{3,5^{2}-left(frac{(5-3)^{2}+3,5^{2}-3^{2}}{2 *(5-3)}right)^{2}}=11,98 mathbf { кв.см} .]

Ответ: S = 11,98 кв.см.

Источник

Площадь прямоугольной трапеции можно найти по любой из формул для площади произвольной трапеции. Некоторые из общих формул могут быть упрощены на основании свойств прямоугольной трапеции.

I. Площадь трапеции равна произведению полусуммы оснований на высоту.

ploshchad-pryamougolnoj-trapeciiПлощадь прямоугольной трапеции ABCD,

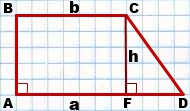
AD∥BC,

    [AB bot AD,CF bot AD]

равна

    [{S_{ABCD}} = frac{{AD + BC}}{2} cdot CF]

Так как меньшая боковая сторона прямоугольной трапеции перпендикулярна основаниям, то она равна высоте трапеции, то есть

    [{S_{ABCD}} = frac{{AD + BC}}{2} cdot AB]

Если обозначить AD=a, BC=b, CF=AB=h, то формула площади прямоугольной трапеции через основания и высоту (меньшую боковую сторону):

    [S = frac{{a + b}}{2} cdot h]

II. Площадь трапеции равна произведению средней линии на высоту.

ploshchad-pryamougolnoj-trapecii-cherez-srednyuyu-liniyuЕсли MN — средняя линия прямоугольной трапеции ABCD,

    [AB bot AD,]

то площадь

    [{S_{ABCD}} = MN cdot AB]

Если обозначить среднюю линию MN=m, меньшую боковую сторону AB=h, получим формулу для нахождения площади прямоугольной трапеции через среднюю линию:

    [S = m cdot h]

III. Площадь трапеции равна половине произведения диагоналей трапеции на синус угла между ними.

ploshchad-pryamougolnoj-trapecii-cherez-diagonaliДля прямоугольной

трапеции

ABCD,

AD∥BC,

    [{S_{ABCD}} = frac{1}{2}AC cdot BD cdot sin angle COD]

Так как sin(180º-α)=sin α, то также 

    [{S_{ABCD}} = frac{1}{2}AC cdot BD cdot sin angle AOD]

Если AC=d1, BD=d2, ∠COD=φ, то

    [S = frac{1}{2}{d_1} cdot {d_2} cdot sin varphi ]

ploshchad-pryamougolnoj-trapecii-cherez-perpendikulyarnye-diagonaliВ частности, если диагонали трапеции перпендикулярны, то

    [S = frac{1}{2}{d_1} cdot {d_2}]

VI. Площадь трапеции равна произведению её полупериметра на радиус вписанной окружности.

ploshchad-pryamougolnoj-trapecii-cherez-radius

    [S = p cdot r]

Так как в трапецию можно вписать окружность, то

AD+BC=AB+CD=p. Следовательно,

    [{S_{ABCD}} = (AD + BC) cdot r]

или

    [{S_{ABCD}} = (AB + CD) cdot r]

Обозначив AD=a, BC=b, CD=c, AB=h=2r, получим формулы площади прямоугольной трапеции через радиус вписанной окружности:

    [S = (a + b) cdot r]

    [S = (2r + c) cdot r]

Если в трапецию вписана окружность, площадь трапеции также можно найти как удвоенное произведение радиуса и средней линии.  Формула

    [S = 2mr]

Если в прямоугольную трапецию вписана окружность, ее площадь равна произведению оснований.

    [{S_{ABCD}} = AD cdot BC]

или

    [S = ab]

Источник

Площадь прямоугольной трапеции найти очень просто: достаточно вспомнить, из что представляет собой эта геометрическая фигура. Трапеция состоит из двух параллельных и двух боковых сторон, причем одна из боковых сторон имеет угол в 90 градусов.

Найти площадь трапеции можно по следующим формулам:

текст при наведении

модератор выбрал этот ответ лучшим

[поль­зоват­ель забло­киров­ан]
[179K]

7 лет назад 

Площадь трапеции равна полусумме её оснований, умноженной на высоту данной трапеции:

S=(( AD+ВС) :2)хВН,

Высотой трапеции является любой перпендикуляр , относительно основаниям трапеции, проведенный из любой точки от одного основания трапеции до другого.

Площадь равнобедренной трапеции можно найти и по формуле:

S=4r:sina;

в этой формуле r– это радиус вписанной в равнобедренную трапецию окружности, sina – угол при основании.

Площадь трапеции равна произведению средней линии трапеции и её высоты:

S=mh,

где h– это высота трапеции, m– её средняя линия.

Есть и ещё одна формула, по которой возможно найти площадь трапеции. В данной формуле:

a и b– это основания, с и d– боковые стороны трапеции.

Что такое прямоугольная трапеция?

Это фигура, у которой две стороны параллельны, третья перпендикулярна первым двум, а четвёртая расположена под определённым, не прямым углом.

Рисунок:

На рисунке вы видите прямоугольную трапецию. Две стороны у неё параллельны (a и c). Сторона b перпендикулярна, а четвёртую сторону мы даже можем не обозначать, так как она нам не понадобится для расчётов.

Теперь посмотрите, что будет, если справа достроить к четвёртой стороне два отрезка так, как изображено на рисунке красным цветом. То есть отрезки должны быть параллельны противоположной стороне трапеции. Как вы видите, получился прямоугольник большей площади, чем наша трапеция. Затем ещё проведём из правого верхнего угла трапеции вниз отрезок, перпендикулярный нижней стороне.

Таким образом наш большой прямоугольник делится на два поменьше. Левый цельный, а правый – состоящий из треугольников.

Площадь трапеции складывается из суммы площади левого прямоугольника и из площади треугольника:

Sтрап = Sab + Sтреуг

Площадь левого прямоугольника равна произведению a на b:

Sab = a * b

А площадь треугольника равна одной второй от площади правого прямоугольника, то есть её половине. Вертикальная сторона этого прямоугольника равна b, а горизонтальная равна разности между большей из параллельных сторон трапеции и меньшей, то есть вертикальная сторона равна c-a.

Получается, что площадь правого прямоугольника равна b(c-a).

Таким образом площадь треугольника равна:

Sтреуг = b(c-a)/2

А искомая площадь трапеции:

Sтрап = ab + b(c-a)/2

Ответ: Площадь прямоугольной трапеции равна ab + b(c-a)/2

Nonse­nse
[63.5K]

7 лет назад 

Вот так выглядит прямоугольная трапеция (ПТ), у неё одна из боковых сторон равна высоте и образует с основаниями прямой угол (90º):

Площадь ПТ — половина суммы длин оснований, умноженная на высоту:

Или произведение средней линии на высоту:

Или половина произведения диагоналей на синус угла между ними:

Или, если диагонали трапеции перпендикулярны, то просто, половине их произведения:

Или полупериметру, помноженному на радиус вписанной окружности:

Или иначе, положив что AD=a, BC=b, CD=c, и AB=h(высота)=2r(двойной радиус или диаметр вписанной окружности):

Или удвоенное произведение радиуса вписанной окружности и средней линии:

Galin­a7v7
[120K]

7 лет назад 

Для ответа именно на этот вопрос- “как найти площадь прямоугольной трапеции АВСД “(АВ | АД) достаточно знать:

1)2 основания ВС =b и АД =а.

2)Высоту трапеции АВ=h

Формула площади S прямоугольной трапеции:

S = (a+b)*h/2

То есть необходимо знать или найти 3 параметра трапеции: оба основания, и боковую сторону, которая перпендикулярна обоим основаниям.

Трапеция которая имеет прямые (90 градусов) углы при боковой стороне называется прямоугольной.

текст при наведении

Площадь прямоугольной трапеции равна сумме площадей прямоугольника с меньшем основанием a и высотой h и прямоугольного треугольника с основанием с и высотой h.

А теперь посчитаем:

площадь прямоугольника равна a*h, а площадь прямоугольного треугольника равна c*h/2 (сторона с=b-a) = (b-a)*h/2

таким образом площадь любой прямоугольной трапеции можно написать в виде:

S(трапеции)=a*h+(b-a)*h/2=(2a*h+(b-a)*h)/2=h(2а+b-a)/2=h(а+b)/2.

а+b у нас сумма оснований трапеции, поэтому

площадь прямоугольной трапеции равна сумме оснований умноженной на половину высоты трапеции

Virin­eya
[16K]

7 лет назад 

Трапеция – это четырехугольник с двумя параллельными друг другу сторонами, являющиеся её основаниями, а две наклонные стороны – её боковыми. Прямоугольная трапеция – это фигура, у которой хотя бы одна сторона имеет угол 90 градусов. Хотя у данной фигуры минимум 2 прямых угла; это трапеция, у которой одна сторона перпендикулярна двум основаниям.

Площадь прямоугольной трапеции ( по сути, ничем не отличается от формулы вычисления площади обычной трапеции, но одна из сторон является высотой): произведение 1/2 суммы её двух оснований и высоты, которая может являться одной из боковых сторон фигуры.

Определяется по формуле: S = 1/2 · (a + b) · h

stalo­nevic­h
[24.6K]

8 лет назад 

У этой фигуры имеются две параллельные стороны (a и b), а также 2 боковые. Для решения необходимо провести высоту, или же эта будет одна из боковых сторон фигуры, которая имеет угол в 90 градусов (пусть будет h), тогда формула имеет вид.

Oleg7­4
[202K]

9 лет назад 

Если взять два основания А и В, которые в геометрической фигуре ” трапеция ” всегда параллельны, сложить их, потом разделить эту сумму пополам и умножить полученный результат на высоту H трапеции, то получим площадь S трапеции.

текст при наведении

Стрым­брым
[372K]

9 лет назад 

Как мы знаем, трапецией называется геометрическая фигура, которая образована четырьмя отрезками, два из которых параллельны между собой. Площадь трапеции определяется, как полусумма оснований, помноженная на высоту.

текст при наведении

Площадь трапеции = H (A + C) / 2

где

А и С – длина каждого основания трапеции

А Н – это высота

Напомним, что основания – это две параллельные стороны трапеции. Высота трапеции – перпендикулярна двум основаниям.

Katal­ina
[24.1K]

9 лет назад 

Мне, если сказать честно, для ответа на этот вопрос пришлось освежить память и покопаться в интернете. Так вот, площадь прямоугольной трапеции равна деленной пополам сумме оснований, умноженной на высоту.

текст при наведении

Гульн­ара Римов­на
[43]

9 лет назад 

Допустим, что основания этой трапеции а( меньшее основание )и в( большее основание), высота- h. тогда, чтобы найти s можно поступить и по- другому. S=a*h+h*(b-a)/2

nasta­sykos
[7]

9 лет назад 

площадь прямоугольной трапеции равна полусумме оснований умноженной на высоту трапеции

Sveta­2013
[95]

9 лет назад 

сумму оснований умножить на высоту и поделить пополам

Знаете ответ?
Источник

Укажите размеры:

Основание 1

Основание 2

Боковая сторона (прямая)

Результат:

Решение:

Скопировать

Ссылка на страницу с результатом:

# Теория

Трапеция – это четырёхугольник у которого две противоположные стороны параллельны и не равны между собой. Параллельные стороны трапеции называются основаниями, а две другие стороны называются боковыми.

Основания трапеции – это две параллельные противоположные стороны.

Высота трапеции – это прямой отрезок проведённый от центра до границы круга. В прямоугольной трапеции высота равна боковой стороне с прямым углом.

Бывают прямоугольная, равнобедренная и неравнобедренная трапеции.

Формула площади трапеции

Чтобы посчитать площадь прямоугольной трапеции, необходимо знать размеры её оснований и боковой стороны с прямым углом.

Площадь прямоугольной трапеции расчитывается по формуле:

a
b
h

S = dfrac{a + b}{2} cdot h

  • S – площадь трапеции
  • a – основание трапиции
  • b – основание трапеции
  • h – боковая сторона с прямым углом

Похожие калькуляторы:

Войдите чтобы писать комментарии

Источник

Площадь прямоугольной трапеции: онлайн калькулятор, формула расчета, пример вычисления

Автор статьи

Сергей Феликсович Савельев

Эксперт по предмету «Калькуляторы»

Задать вопрос автору статьи

Ниже вы узнаете, как выглядят формулы для нахождения площади прямоугольной трапеции, а также сможете воспользоваться онлайн-калькуляторами для её расчёта.

Определение 1

Особенность прямоугольной трапеции в том, что её высота равна стороне, расположенной перпендикулярно двум основаниям.

Для того чтобы вычислить площадь прямоугольной трапеции через 3 её стороны, воспользуйтесь нашим онлайн-калькулятором. Для расчёта введите имеющиеся данные в поля для ввода.

Площадь прямоугольной трапеции

Площадь прямоугольной трапеции

Высота прямоугольной трапеции $h$ равна длине стороны $c$, расположенной под прямым углом к двум основаниям трапеции $a$ и $c$.

Следовательно, формула для вычисления площади прямоугольной трапеции имеет вид:

$S = frac12 cdot (a + c) cdot b$, где

$a$ — малое основание;

$с$ — большее основание;

$b$ — перпендикулярная основаниям сторона.

Пример 1

Задача

Дана прямоугольная трапеция, сторона $b$ у которой равна $2.32$ см, сторона $a$ составляет $2.42$, и сторона $c$ равна $3.94$ см. Чему равна площадь трапеции?

Решение:

Воспользуемся приведённой выше формулой:

$S =frac{(2.42 + 3.93) cdot 2.32}{2} = 7.37$ кв. см.

Проверим ответ с помощью онлайн-калькулятора. Значения совпадают, а значит, решение найдено верно.

Также площадь прямоугольной трапеции можно рассчитать и по другим формулам, общим для всех видов трапеций, например, через среднюю линию и высоту. Высоту в формуле также можно заменить на сторону, перпендикулярную основаниям.

Площадь трапеции по высоте и средней линии

Площадь трапеции по высоте и средней линии

Формула нахождения площади трапеции по высоте и средней линии:

$S = m cdot h$, где

$S$ – площадь трапеции,

$m$ – средняя линия,

$h$ – высота трапеции.

Другой способ расчёта площади прямоугольной трапеции — через длины оснований и два угла, расположенных при одном основании.

Площадь трапеции через ее основание и углы

Площадь трапеции через ее основание и углы

Формула нахождения площади трапеции через ее основание и углы при основании:

$S = frac12 cdot (b^2 – g^2) cdot frac{sin (α) cdot sin (γ)}{sin (α + γ)}$, где

$S$ – площадь трапеции,

$b$ – большее основание,

$g$ – малое основание,

$α$ – первый угол при основании,

$γ$ – второй угол при основании.

Также площадь прямоугольной трапеции можно найти через диагонали и угол между ними.

Площадь трапеции по диагонали и углу между диагоналями

Площадь трапеции по диагонали и углу между диагоналями

Формула нахождения площади трапеции по диагонали и углу между диагоналями:

$S =frac12 cdot d1 cdot d2 cdot sin (α)$, где

$S$ – площадь трапеции,

$d1$ – первая диагональ,

$d2$ – вторая диагональ,

$α$ – угол между диагоналями.

Рассмотрим пример.

Пример 2

Задача

Дана прямоугольная трапеция с диагоналями $d1$ и $d2$, равными $2.22$ см и $2.64$ см. Угол между диагоналями $α$ равен $56°$. Чему равна площадь прямоугольной трапеции?

Решение:

Синус заданного угла $α$ равен $0.83$, найти его можно по специальным таблицам, приведённым на нашем сайте. Теперь подставим все известные значения:

$S = frac{2.22 cdot 2.64 cdot 0.83}{2} = 2.43$ кв. см.

Вычисленный ответ совпадает с ответом онлайн-калькулятора, а значит, решение — верное.

И наконец, рассмотрим случай когда нет данных о том, какие стороны являются основаниями, а какая сторона расположена под прямым углом, но при этом известны все стороны трапеции.

Площадь трапеции по четырём сторонам

Площадь трапеции по четырём сторонам

Формула нахождения площади трапеции по четырём сторонам выглядит следующим образом:

$S = frac{a + b}{2} cdot sqrt{c^2 – (frac{(b – a)^2 + c^2 – d^2}{2 cdot (b – a)})^2}$, где

$S$ – площадь трапеции,

$a$ – малое основание,

$b$ – большее основание,

$c, d$ – боковые стороны.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата написания статьи: 26.06.2019

Источник

Добавить комментарий