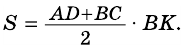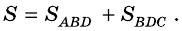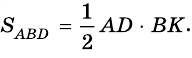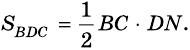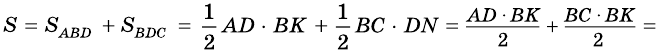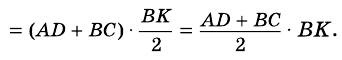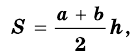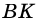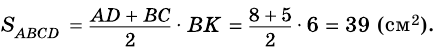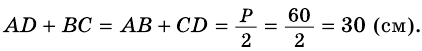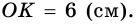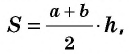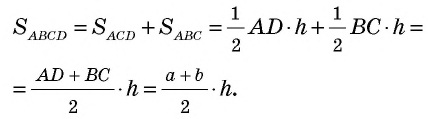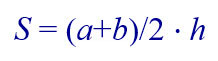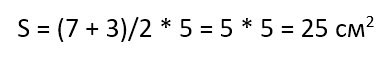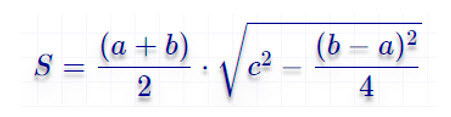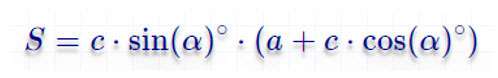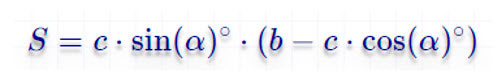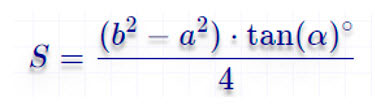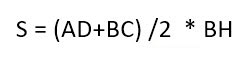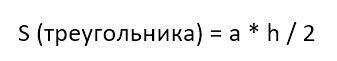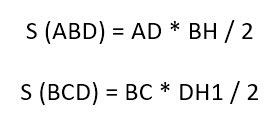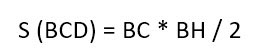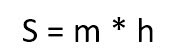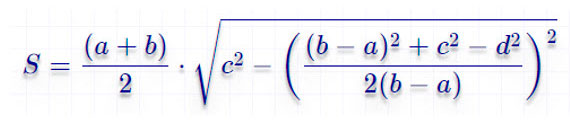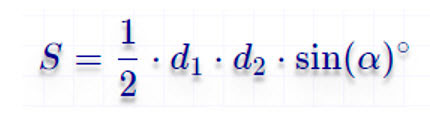Практика прошлогодних ЕГЭ и ГИА показывает, что задачи по геометрии вызывают сложности у многих школьников. Вы легко справитесь с ними, если заучите все нужные формулы и попрактикуетесь в решении задач.
В этой статье вы увидите формулы нахождения площади трапеции, а также примеры задач с решениями. Такие же могут попасться вам в КИМах на аттестационных экзаменах или на олимпиадах. Поэтому отнеситесь к ним внимательно.
Что нужно знать про трапецию?
Для начала вспомним, что трапецией называется четырехугольник, у которого две противоположные стороны, их еще называют основаниями, параллельны, а две другие – нет.
В трапеции также может быть опущена высота (перпендикуляр к основанию). Проведена средняя линия – это прямая, которая параллельна основаниям и равна половине их суммы. А также диагонали, которые могут пересекаться, образуя острые и тупые углы. Или, в отдельных случаях, под прямым углом. Кроме того, если трапеция равнобедренная, в нее можно вписать окружность. И описать окружность около нее.
Формулы площади трапеции
Для начала рассмотрим стандартные формулы нахождения площади трапеции. Способы вычислить площадь равнобедренной и криволинейной трапеций рассмотрим ниже.
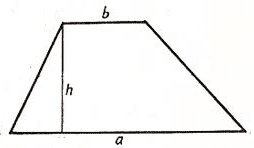
Итак, представьте, что у вас есть трапеция с основаниями a и b, в которой к большему основанию опущена высота h. Вычислить площадь фигуры в таком случае проще простого. Надо всего лишь разделить на два сумму длин оснований и умножить то, что получится, на высоту: S = 1/2(a + b)*h.
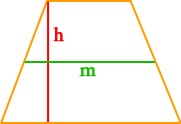
Возьмем другой случай: предположим, в трапеции, кроме высоты, проведена средняя линия m. Нам известна формула нахождения длины средней линии: m = 1/2(a + b). Поэтому с полным правом можем упростить формулу площади трапеции до следующего вида: S = m* h. Другими словами, чтобы найти площадь трапеции, надо умножить среднюю линию на высоту.
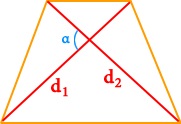
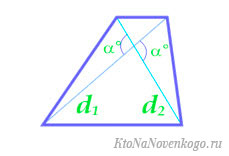
Рассмотрим еще один вариант: в трапеции проведены диагонали d1и d2, которые пересекаются не под прямым углом α. Чтобы вычислить площадь такой трапеции, вам нужно разделить на два произведение диагоналей и умножить то, что получится, на sin угла между ними: S= 1/2d1d2 *sinα.
Теперь рассмотрим формулу для нахождения площади трапеции, если о ней неизвестно ничего, кроме длин всех ее сторон: a, b, c и d. Это громоздкая и сложная формула, но вам будет полезно запомнить на всякий случай и ее: S = 1/2(a + b) * √c2 – ( ( 1/2(b – a)) * ((b – a)2 + c2 – d2) )2.
Кстати, приведенные выше примеры верны и для того случая, когда вам потребуется формула площади прямоугольной трапеции. Эта трапеция, боковая сторона которой примыкает к основаниям под прямым углом.
Равнобедренная трапеция
Трапеция, боковые стороны которой равны, называется равнобедренной. Мы рассмотрим несколько вариантов формулы площади равнобедренной трапеции.
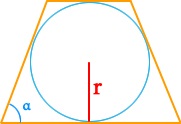
Первый вариант: для случая, когда внутрь равнобедренной трапеции вписана окружность с радиусом r, а боковая сторона и большее основание образуют острый угол α. Окружность может быть вписана в трапецию при условии, что сумма длин ее оснований равна сумме длин боковых сторон.
Площадь равнобедренной трапеции вычисляется так: умножьте квадрат радиуса вписанной окружности на четыре и разделите все это на sinα: S = 4r2/sinα. Еще одна формула площади является частным случаем для того варианта, когда угол между большим основанием и боковой стороной равен 300: S = 8r2.
Второй вариант: на этот раз возьмем равнобедренную трапецию, в которой вдобавок проведены диагонали d1 и d2, а также высота h. Если диагонали трапеции взаимно перпендикулярны, высота составляет половину суммы оснований: h = 1/2(a + b). Зная это, легко преобразовать уже знакомую вам формулу площади трапеции в такой вид: S = h2.
Формула площади криволинейной трапеции
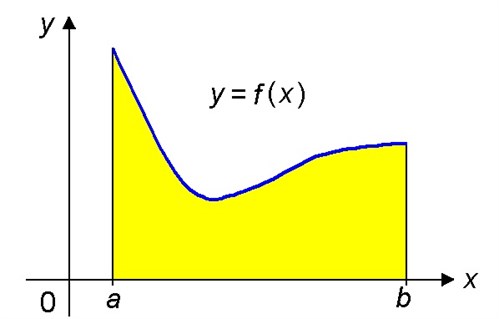
Начнем с того, что разберемся: что такое криволинейная трапеция. Представьте себе ось координат и график непрерывной и неотрицательной функции f, которая не меняет знака в пределах заданного отрезка [a; b] на оси x. Криволинейную трапецию образуют график функции у = f(x) – вверху, ось х – внизу (отрезок [a; b]), а по бокам – прямые, проведенные между точками a и b и графиком функции.
Вычислить площадь такой нестандартной фигуры нельзя приведенными выше способами. Тут нужно применить математический анализ и использовать интеграл. А именно: формулу Ньютона-Лейбница – S = ∫baf(x)dx = F(x)│ba = F(b) – F(a). В этой формуле F – первообразная нашей функции на выбранном отрезке [a; b]. И площадь криволинейной трапеции соответствует приращению первообразной на заданном отрезке.
Примеры задач
Чтобы все эти формулы лучше улеглись в голове, вот вам несколько примеров задач на нахождение площади трапеции. Лучше всего будет, если вы сперва попробуете решить задачи сами, и только потом сверите полученный ответ с готовым решением.
Задача №1: Дана трапеция. Ее большее основание – 11 см, меньшее – 4см. В трапеции проведены диагонали, одна длиной 12 см, вторая – 9 см.
Решение: Постройте трапецию АМРС. Проведите прямую РХ через вершину Р так, чтобы она оказалась параллельной диагонали МС и пересекла прямую АС в точке Х. Получится треугольник АРХ.
Мы рассмотрим две полученных в результате этих манипуляций фигуры: треугольник АРХ и параллелограмм СМРХ.
Благодаря параллелограмму мы узнаем, что РХ = МС = 12 см и СХ = МР = 4см. Откуда можем вычислить сторону АХ треугольника АРХ: АХ = АС + СХ = 11 + 4 = 15 см.
Мы также можем доказать, что треугольник АРХ – прямоугольный (для этого примените теорему Пифагора – АХ2 = АР2 + РХ2). И высчитать его площадь: SAPX = 1/2(AP * PX) = 1/2(9 * 12) = 54 см2.
Дальше вам потребуется доказать, что треугольники АМР и РСХ являются равновеликими. Основанием послужит равенство сторон МР и СХ (уже доказанное выше). А также высоты, которые вы опустите на эти стороны – они равны высоте трапеции АМРС.
Все это позволит вам утверждать, что SAMPC = SAPX = 54 см2.
Задача №2: Дана трапеция КРМС. На ее боковых сторонах расположены точки О и Е, при этом ОЕ и КС параллельны. Также известно, что площади трапеций ОРМЕ и ОКСЕ находятся в соотношении 1:5. РМ = а и КС = b. Требуется найти ОЕ.
Решение: Проведите через точку М прямую, параллельную РК, и точку ее пересечения с ОЕ обозначьте Т. А – точка пересечения прямой, проведенной через точку Е параллельно РК, с основанием КС.
Введем еще одно обозначение – ОЕ = х. А также высоту h1 для треугольника ТМЕ и высоту h2 для треугольника АЕС (вы можете самостоятельно доказать подобие этих треугольников).
Будем считать, что b > а. Площади трапеций ОРМЕ и ОКСЕ относятся как 1:5, что дает нам право составить такое уравнение: (х + а) * h1 = 1/5(b + х) * h2. Преобразуем и получим: h1/ h2 = 1/5 * ((b + х)/(х + а)).
Раз треугольники ТМЕ и АЕС подобные, имеем h1/ h2 = (х – а)/( b – х). Объединим обе записи и получим: (х – а)/(b – х) = 1/5 * ((b + х)/(х + а)) ↔ 5(х – а)(х + а) = (b + х)(b – х) ↔ 5(х2 – а2) = (b2 – х2) ↔ 6х2 = b2 + 5а2 ↔ х = √(5а2 + b2)/6.
Таким образом, ОЕ = х = √(5а2 + b2)/6.
Также советуем посмотреть вам наше новое видео по теме нахождения площади фигур, в том числе и трапеции:
Заключение
Геометрия не самая легкая из наук, но вы наверняка сможете справиться с экзаменационными заданиями. Достаточно проявить немного усидчивости при подготовке. И, конечно, запомнить все нужные формулы.
Мы постарались собрать в одном месте все формулы вычисления площади трапеции, чтобы вы могли воспользоваться ими, когда будете готовиться к экзаменам и повторять материал.
Обязательно расскажите про эту статью одноклассникам и друзьям в социальных сетях. Пускай хороших оценок за ЕГЭ и ГИА будет больше!
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Выбирайте формулу в зависимости от известных величин.
1. Как найти площадь трапеции через основания и высоту
Посчитайте сумму оснований трапеции.
Умножьте результат на высоту и поделите на два.
- S – искомая площадь трапеции.
- a и b – основания трапеции (её параллельные стороны).
- h – высота трапеции.
2. Как вычислить площадь трапеции через высоту и среднюю линию
Просто умножьте высоту трапеции на среднюю линию.
- S – искомая площадь трапеции.
- m – средняя линия трапеции (отрезок, соединяющий середины боковых сторон).
- h – высота трапеции.
3. Как найти площадь трапеции через диагонали и угол между ними
Умножьте одну диагональ на другую, а затем — на синус любого угла между ними.
Поделите результат на два.
- S – искомая площадь трапеции.
- x и y – диагонали трапеции.
- α – любой угол между диагоналями.
4. Как найти площадь трапеции через четыре стороны
Отнимите от большего основания меньшее.
Найдите квадрат полученного числа.
Прибавьте к результату квадрат одной боковой стороны и отнимите квадрат второй.
Поделите полученное число на удвоенную разность оснований.
Найдите квадрат результата и отнимите его от квадрата боковой стороны.
Найдите корень из полученного числа.
Умножьте результат на половину от суммы оснований.
- S – искомая площадь трапеции.
- a, b – основания трапеции.
- c, d – боковые стороны.
5. Как вычислить площадь равнобедренной трапеции через четыре стороны
Отнимите от большего основания трапеции меньшее и поделите результат на два.
Найдите квадрат полученного числа и отнимите его от квадрата боковой стороны.
Найдите корень из результата.
Умножьте полученное число на сумму оснований и поделите на два.
- S — искомая площадь трапеции.
- a, b — основания трапеции.
- c, d — боковые стороны (напомним, в равнобедренной трапеции они равны).
6. Как найти площадь равнобедренной трапеции через радиус вписанной окружности и угол
Найдите квадрат радиуса и умножьте его на четыре.
Поделите результат на синус известного угла.
- r — радиус вписанной окружности.
- α — любой угол трапеции.
Читайте также 📐✏️🎓
- 8 способов найти длину окружности
- 8 способов найти периметр треугольника
- 7 способов найти площадь прямоугольника
- Как перевести обычную дробь в десятичную
- Как освоить устный счёт школьникам и взрослым
Трапеция — это четырехугольник, в котором две противоположные стороны параллельны.
Онлайн-калькулятор площади трапеции
Введем некоторые понятия, которые в дальнейшем помогут решить задачи, связанные с нахождением площади данной фигуры.
Основания трапеции — это стороны, параллельные друг другу.
Боковые стороны — соответственно, две оставшиеся стороны.
Средняя линия — отрезок, который соединяет центры боковых сторон. Эта линия всегда параллельна основаниям трапеции.
Виды трапеций
Трапеция бывает трех видов:
- Равнобедренная – та, у которой боковые стороны равны.
- Прямоугольная, у которой два углы прямые, т. е. равны 90 градусам.
- Произвольная, которая не относится к двум вышеописанным категориям.
Площадь трапеции можно найти различными способами. Разберем их более подробно и закрепим материал решением простых задач.
Формула площади трапеции по основанию и высоте
Пусть нам дана произвольная трапеция. Чтобы найти ее площадь, воспользуемся следующей формулой:
S=a+b2⋅hS=frac{a+b}{2}cdot h
a,ba, b — основания трапеции;
hh — высота трапеции.
Найти площадь SS трапеции, в которой известны основания, численно равные 10 (см.) и 8 (см.) и высота, длиной 6 (см.).
Решение
a=8a=8
b=10b=10
h=6h=6
Сразу подставляем числа в имеющуюся у нас формулу и вычисляем искомую величину:
S=a+b2⋅h=8+102⋅6=54S=frac{a+b}{2}cdot h=frac{8+10}{2}cdot 6=54 (см. кв.)
Ответ: 54 см. кв.
Формула площади трапеции по основанию и средней линии
Нужно упомянуть, что средняя линия трапеции равна половине суммы ее оснований. Тем самым, способ нахождения площади через среднюю линию есть не что иное, как способ, аналогичный первому. Поскольку:
l=a+b2,l=frac{a+b}{2},
то:
S=l⋅hS=lcdot h
ll — средняя линия трапеции;
hh — высота.
Найти площадь трапеции, если известно, что средняя линия равна 5 (см.), а высота трапеции в 2 раза больше её.
Решение
l=5l=5
h=2⋅lh=2cdot l
Найдем высоту трапеции:
h=2⋅5=10h=2cdot 5=10
Площадь:
S=l⋅h=5⋅10=50S=lcdot h=5cdot 10=50 (см. кв.)
Ответ: 50 см. кв.
Формула площади трапеции по всем сторонам
Данный способ подходит для тех случаев, когда в задаче известны все 4 стороны нашей трапеции.
S=a+b2c2−((b−a)2+c2−d22⋅(b−a))2S=frac{a+b}{2}sqrt{c^2-big(frac{(b-a)^2+c^2-d^2}{2cdot(b-a)}big)^2}
Даны длины всех сторон трапеции. Основания равны 10 (см.) и 5 (см.), боковые стороны: 4 (см.) и 3 (см.). Найти площадь фигуры.
Решение
a=5a=5
b=10b=10
c=4c=4
d=3d=3
Тогда:
S=a+b2c2−((b−a)2+c2−d22⋅(b−a))2=15216−(25+16−910)2=18S=frac{a+b}{2}sqrt{c^2-big(frac{(b-a)^2+c^2-d^2}{2cdot(b-a)}big)^2}=frac{15}{2}sqrt{16-big(frac{25+16-9}{10}big)^2}=18 (см. кв.)
Ответ: 18 см. кв.
Формула площади трапеции через диагонали и угол между ними
S=12⋅d1⋅d2⋅sin(α)S=frac{1}{2}cdot d_1cdot d_2cdotsin(alpha)
d1,d2d_1, d_2 — диагонали трапеции;
αalpha — угол между диагоналями.
Пусть две диагонали трапеции равны 20 (см.) и 7 (см.) и при пересечении они образуют угол 30 градусов. Найти площадь трапеции SS.
Решение
d1=20d_1=20
d2=7d_2=7
α=30∘alpha=30^{circ}
Площадь:
S=12⋅d1⋅d2⋅sin(α)=12⋅20⋅7⋅sin(30∘)=35S=frac{1}{2}cdot d_1cdot d_2cdotsin(alpha)=frac{1}{2}cdot20cdot 7cdotsin(30^{circ})=35 (см. кв.)
Ответ: 35 см. кв.
Формула площади трапеции через радиус вписанной окружности и угол
Этот случай подходит только для равнобедренной трапеции.
S=4⋅r2sin(α)S=frac{4cdot r^2}{sin(alpha)}
rr — радиус вписанной окружности;
αalpha — угол между основанием и боковой стороной.
Дан радиус вписанной окружности в трапецию, равный 4 (см.). Угол αalpha равный 90 градусам. Найти площадь трапеции.
Решение
r=4r=4
α=90∘alpha=90^{circ}
По формуле:
S=4⋅r2sin(α)=4⋅16=64S=frac{4cdot r^2}{sin(alpha)}=4cdot 16=64 (см. кв.)
Ответ: 64 см. кв.
Хотите заказать контрольную работу по геометрии? У нас самые низкие цены среди конкурентов!
Тест по теме «Площадь трапеции»
Преподаватель который помогает студентам и школьникам в учёбе.
Площадь трапеции – определение и вычисление с примерами решения
Теорема (о площади трапеции). Площадь трапеции равна произведению полусуммы ее оснований на высоту.
Доказательство:
Пусть
Докажем, что площадь 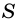
1) Диагональ 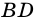
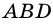
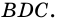
2) 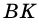
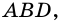
3) Проведем в трапеции высоту 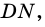
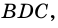
4) 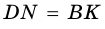
В общем виде формулу площади 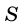
где 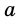
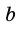
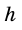
Следствие. Площадь трапеции равна произведению ее средней линии на высоту.
Пример:
В трапеции 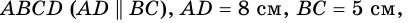
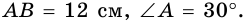
Решение:
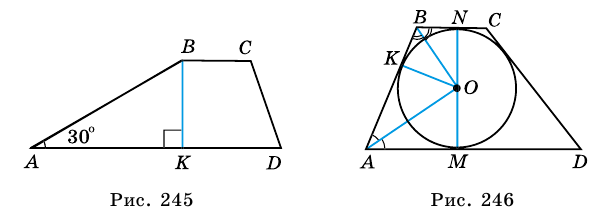
1) Проведем в трапеции 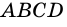
(рис. 245). В 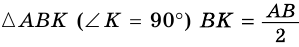
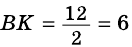
2)
Ответ. 39
Пример:
Периметр трапеции 60 см, а одна из боковых сторон точкой касания вписанной окружности делится на отрезки 9 см и 4 см. Найдите площадь трапеции.
Решение:
1) Так как трапеция является описанной около окружности (рис. 246), то
2) Центр вписанной окружности – точка 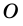
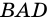
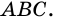
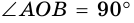
3) Точка 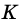
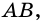
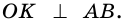
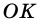
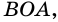
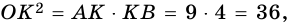
4) 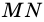
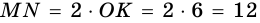
5) Следовательно,
Ответ. 180
Площадь трапеции
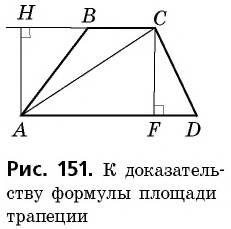
Часто для вычисления площади некоторого многоугольника его разбивают на несколько треугольников и находят искомую площадь как сумму площадей этих треугольников. Именно такой подход можно применить для вывода формулы площади трапеции.
Теорема (формула площади трапеции) Площадь трапеции равна произведению полусуммы ее оснований на высоту:
где 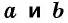
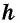
Доказательство:
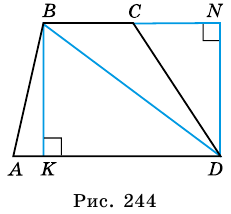
Пусть дана трапеция 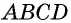
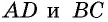
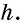
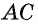
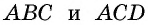
Проведем высоты этих треугольников 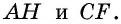
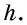
Теорема доказана.
Следствие
Площадь трапеции равна произведению средней линии на высоту.
- Центральные и вписанные углы
- Углы и расстояния в пространстве
- Подобие треугольников
- Решение прямоугольных треугольников
- Прямоугольник и его свойства
- Ромб и его свойства, определение и примеры
- Квадрат и его свойства
- Трапеция и ее свойства
Как найти площадь обычной и равнобедренной трапеции
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. В этой статье мы расскажем, как посчитать площадь трапеции. Эту тему подробно изучают в школе в 8-м классе.
Но в классической программе учителя дают далеко не все формулы, с помощью которых можно вычислить нужное значение. И ограничиваются, как правило, одной или двумя.
Мы же дадим максимально развернутый ответ на этот вопрос. Ведь трапеция – это весьма примечательная и сложная фигура в геометрии. А соответственно, и формулы для вычисления ее площади отличаются определенной сложностью и громоздкостью.
Тут нет банальных «перемножить длины сторон», как у площади прямоугольника. Все гораздо мудреней.
Что такое трапеция
Но для начала будет нелишним напомнить, что из себя представляет эта геометрическая фигура.
Трапеция – это геометрическая фигура, которая является четырехугольником, и у которой две противоположные стороны параллельны.
Последнее утверждение очень важное. ТОЛЬКО ДВЕ противоположные стороны параллельны у трапеции. Ведь если бы обе пары лежали на параллельных прямых, то это был бы уже параллелограмм.
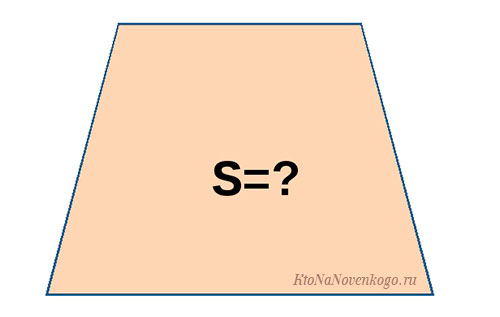
Вот так выглядит трапеция:
А вот так параллелограмм:
Кстати, именно по этому принципу древний математик Евклид и разделил все четырехугольники на две большие категории.
Именно он впервые описал разные геометрические фигуры, в том числе трапеции и параллелограммы. И все свои соображения подробно изложил в книге «Начала», которая датируется 300 годом до нашей эры.
Раз уж мы решили вычислять эту величину, напомним, что она обозначает.
Площадь – это численное значение геометрической фигуры, нарисованной в двухмерном (плоском) пространстве. А проще говоря, это пространство, которое ограничено границами фигуры, и находится как бы внутри нее.
В нашем случае – это область, закрашенная синим цветом:
Кстати, в древности вместо этого термина говорили «квадратура». Считалось, что любую фигуру можно разбить на равные квадраты со стороной «один». Частично это понятие докатилось и до наших дней.
Ведь именно в «квадратных метрах» мы измеряем площадь комнаты/квартиры/дачи/офиса. И в «квадратных километрах» частенько озвучивают размер какой-то территории. Например, когда в телевизионных новостях говорят о масштабах лесных пожаров или наводнений.
Главная формула для вычисления площади трапеции
Та формула, которую изучают в школе, основана на вычислении площади трапеции по длине ее оснований и высоте.
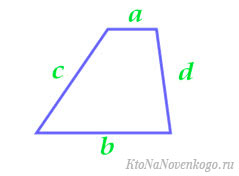
Основания трапеции – это стороны, которые лежат на параллельных прямых. Другая пара сторон называется боковыми.
Высота – это отрезок, проведенный из вершины любого угла к противоположному основанию под углом 90 градусов.
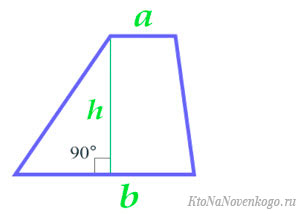
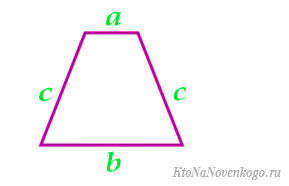
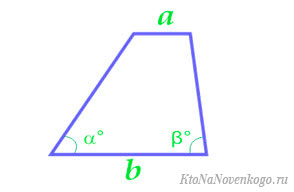
То есть мы имеем вот такие исходные данные:
Здесь «a» и «b» являются основаниями, а «h» — высотой.
И тогда формула для вычисления площади выглядит вот так:
Например, если длины сторон и высота равны:
- a = 7 см
- b = 3 см
- h = 5 см
то площадь такой трапеции будет равна:
Опять же заметьте, если стороны и высота у трапеции обозначались в сантиметрах, то площадь будет измеряться в квадратных сантиметрах (то самое понятие «квадратуры», о котором мы писали выше).
То же самое – миллиметры/квадратные миллиметры, метры/квадратные метры, километры/квадратные километры и так далее.
Формулы площади для равнобедренной трапеции
Равнобедренная трапеция – та, у которой боковые стороны равны. А соответственно, они еще и соприкасаются с основаниями под одинаковыми углами.
Это частный случай, и для него верны все перечисленные формулы. Но с учетом равенства сторон и углов формулы заметно упрощаются.
По четырем сторонам
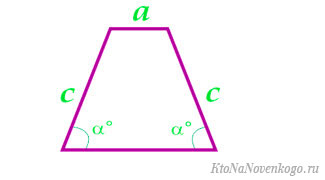
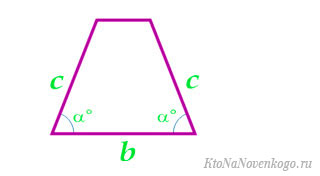
По малому основанию, боковой стороне и углу у большого основания
По большому основанию, углу при нем и боковой стороне
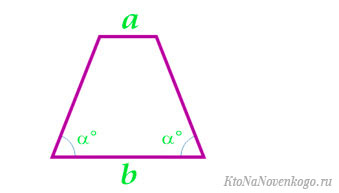
По основаниям и углам
Как видите, формулы громоздкие и весьма сложные сами по себе. Без калькулятора здесь точно не обойтись. С другой стороны, они крайне редко применяются. И служат скорее дополнительными средствами.
Доказательство теоремы о площади трапеции
Любая формула в геометрии требует доказательства. И в нашем случае, формулы вычисления площади трапеции также доказывают во время уроков.
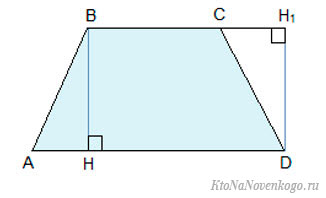
Возьмем для примера трапецию:
В ней AD и BC – основания, BH – высота. Нам надо доказать, что:
Доказательство строится на том, что если провести диагональ BD, то она разделит нашу трапецию на два треугольника. Это будут треугольники ABD и BCD.
И чтобы получить площадь нашей трапеции, нужно посчитать отдельно площади этих треугольников и сложить их.
А как вычислять площадь треугольника, мы уже знаем (или должны знать, согласно школьному курсу). Надо перемножить длину его основания и высоту и поделить на два.
У треугольника ABD высота – это BH. А у треугольника BCD в силу его выпуклости нам пришлось продлить зрительно основание BC, чтобы получить высоту DH1.
И получается:
Но в случае с трапецией высоты равны, то есть BH = DH1. И тогда формулу площади для второго треугольника можно заменить на:
И наконец, с учетом всего вышесказанного начинаем вычислять площадь нашей трапеции. Она равна:
Как часто говориться на уроках геометрии – что и требовалось доказать!
Извиняемся за столь подробное описание доказательства. Но, во-первых, это требуется в рамках школьной программы. А во-вторых, всегда ведь интересно докопаться до самой сути и понять, как и почему именно так что-то устроено.
Как еще можно ее найти (другие формулы)
На этот раз мы уже не будем приводить подробные доказательства каждой из формул. Иначе это займет слишком много времени и места. Просто поверьте, все они правильные и по ним можно вычислить площадь трапеции.
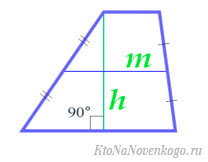
По высоте и средней линии
Средняя линия – это та, которая делит боковые стороны трапеции на две равные части. Формула площади выглядит совсем просто:
По четырем сторонам
Тут формула гораздо сложнее:
Площадь трапеции через диагонали
По основанию и углам при нем
Вот и все, что мы хотели рассказать о том, как вычислять площадь трапеции.