Для решения задачи из верхних угловых точек трапеции опустим перпендикуляры на ее основание. Потом сделаем чертеж с обозначениями полученных точек.

У нас таким образом трапеция разделилась на три геометрические фигуры
Прямоугольник в центре АДЕN
и два треугольника
СДЕ – назовем его первым
АВN – назовем его вторым
Что нам известно из условия.
В первом треугольнике Угол СДЕ будет равен 60 градусам, поскольку 150 – 90 = 60.
Это прямоугольный треугольник, Следовательно угол ДСЕ будет равен 30 градусам
Гипотенуза известна – 7. Известно также свойство такого треугольника: катет, лежащий против угла в 30 градусов равен половине гипотенузы

ДЕ отрезок равен 3,5. Он же является высотой трапеции.
Теперь у нас есть все данные, чтобы вычислить площадь трапеции.
Есть несколько формул, нам подойдет первая:

Половина суммы верхнего и нижнего оснований умножаем на высоту.ДЕ
(6 + 18) : 2 = 12
12 * 3,5 = 42
Ученик
(78),
закрыт
13 лет назад
Катя Дворянинова
Мастер
(1173)
13 лет назад
1) Опустим из вершины B перпендикуляр на отрезок АD. Получим ВЕ – высота трапеции.
2) Из треугольника ВЕА, Е = 90 градусов, найдём ВЕ. Нам известно, что угол В в трапеции АВСD равен 150 градусов. Проведя перпендикуляр ВЕ мы получили градусную меру угла В в треугольнике ВЕА, равную 150 – 90 = 60 градусов.
По свойству суммы внутренних углов треугольника
угол А = 180 – 90 – 60 = 30 градусов.
Катет, лежащий против угла в 30 градусов (ВЕ) , равен половине гипотенузы (АВ) . Тогда
ВЕ = АВ / 2 = 10 / 2 = 5 см.
3) Площадь трапеции равна полусумме оснований, умноженной на высоту:
S = h * (AD + BC) / 2 = 5 * (14 + 30) / 2 = 110 см в квадрате.
ilia p
Мастер
(1423)
13 лет назад
Основания у трапеции параллельны, если из b опустим перпендикуляр h получим что угол abh=150-90, отсюда третий угол равен 30.
Sin (30)*10(14+30)
Светлана Сысуева
Ученик
(116)
13 лет назад
Ответ: 110 кв. см. Угол bac=30гр. Проведем высоту bh. Катет, лежащий против стороны в 30 гр. равен половине гипотенузы, то есть 10:2=5. Площадь трапеции равна (bc+ad) :2 Х bh = (14+30):2 Х 5 = 110 (кв. см)
дима писаревский
Знаток
(325)
13 лет назад
все очень легко, площадь равно 1/2 основания на высоту, основания bc и ad извесны, высота находится следующим образом: проводим из вершины b перпендикуляр на основание ad(точку назовем h), получаем прямоугольный треугольник abh, нам нужно найти bh.
т. к. угол b 150 градусов, угол a=30 градусов, следовательно по теореме: сторона, лежащая против угла в 30 градусов ( толькопрямоугольном треугольнике) равна 1/2 гипотенузы, получаем bh = 5. Находи S:
S= (14+30)*12*5= 110 см^2
Карина
Мастер
(2433)
13 лет назад
1.Угол А = (360-(150+150)/2=30 градусов
2.BH = AB/2=5 см (теорема : катет, лежащий против угла в 30 градусов, равен половине гипотенузы) .
3.Площадь ABCD = (AD+BC)/2 * BH = (30 + 14)/2 * 5 = 110 см квадратных. 

Основания трапеции=3 и 15, боковая сторона=2, образует с одним из оснований трапеции угол 150. Найдите площадь трапеции.
Ответ:9, распишите решение пожалуйста!(15 баллов)
Перейти к контенту
Задание
Основания трапеции равны 10 и 20, боковая сторона, равная 8, образует с одним из оснований трапеции угол 150°. Найдите площадь трапеции.
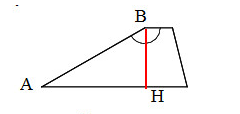
- Проведем высоту BH (см. рис). Рассмотрим треугольник ABH. Данный треугольник прямоугольный с прямым углом H. По условию гипотенуза AB=8.
- ∠А=180°-150°=30° (так как сумма углов трапеции, прилежащих к боковой стороне, равна 180°)
- Из определения ситуса выразим катет BH:
Синус — это отношение противолежащего катета к гипотенузе
sinA=BH/AB
BH = sinA*AB = sin30°*8 = 0,5*8 = 4
Осталось найти площадь трапеции:
S = (10+20)/2*4 = 60
Ответ: 60
Площадь трапеции
- Главная
- /
- Математика
- /
- Геометрия
- /
- Площадь трапеции
Чтобы найти площадь трапеции воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Через длины оснований и высоту

Чему равна площадь трапеции, если:
основание a =
основание b =
высота h =
Ответ: S =
0
ед.²
Округление ответа:
Чему равна площадь трапеции если известны основания a и b, а также высота h?
Формула
S = ½ ⋅ (a + b) ⋅ h
Пример
Если у трапеции основание a = 3 см, основание b = 6 см, а высота h = 4 см, то её площадь:
S = ½ ⋅ (3 + 6) ⋅ 4 = 36 / 2 = 18 см²
Через среднюю линию и высоту
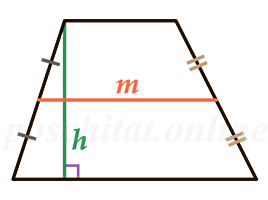
Чему равна площадь трапеции, если:
средняя линия m =
высота h =
Ответ: S =
0
ед.²
Округление ответа:
Чему равна площадь трапеции если известны средняя линия m и высота h?
Формула
S = m ⋅ h
Пример
Если у трапеции средняя линия m = 6 см, а высота h = 4 см, то её площадь:
S = 6 ⋅ 4 = 24 см²
Через длины сторон и оснований
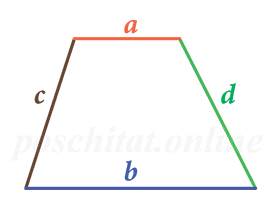
Чему равна площадь трапеции, если:
основание a =
основание b =
сторона c = сторона d =
Ответ: S =
0
ед.²
Округление ответа:
Чему равна площадь трапеции если известны основания a и b, а также стороны c и d?
Формула
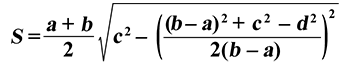
Пример
Если у трапеции основание a = 2 см, основание b = 6 см, сторона c = 4 см, а сторона d = 7 см, то её площадь:
S ≈ 13.555 см²
Через диагонали и угол между ними
Чему равна площадь трапеции, если:
диагональ d1 =
диагональ d2 =
угол α =
Ответ: S =
0
ед.²
Округление ответа:
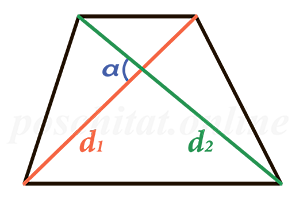
Чему равна площадь трапеции если известны диагонали d1 и d2 и угол между ними α?
Формула
S = ½ ⋅ d1 ⋅ d2 ⋅ sin(α)
Пример
Если у трапеции одна диагональ d1 = 5 см, другая диагональ d2 = 7 см, а угол между ними ∠α = 30°, то её площадь:
S = ½ ⋅ 5 ⋅ 7 ⋅ sin (30) = 17.5 ⋅ 0.5= 8.75 см²
Площадь равнобедренной трапеции
Через среднюю линию, боковую сторону и угол при основании
Чему равна площадь трапеции, если:
средняя линия m =
сторона c =
угол α =
Ответ: S =
0
ед.²
Округление ответа:
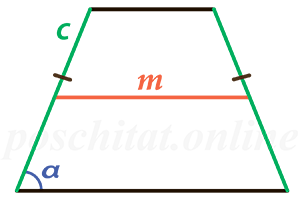
Чему равна площадь равнобедренной трапеции если средняя линия m, боковая сторона с, a угол при основании α?
Формула
S = m ⋅ c ⋅ sin(α)
Пример
Если у равнобедренной трапеции средняя линия m = 6 см, сторона c = 4 см, а угол при основании ∠α = 30°, то её площадь:
S = 6 ⋅ 4 ⋅ sin (30) = 24 ⋅ 0.5 = 12 см²
Через радиус вписанной окружности
Чему равна площадь трапеции, если:
радиус r =
угол α =
Ответ: S =
0
ед.²
Округление ответа:
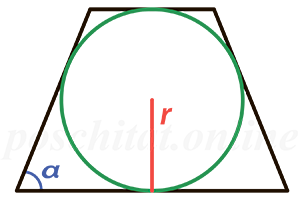
Чему равна площадь равнобедренной трапеции если радиус вписанной окружности r, a угол при основании α?
Формула
S = 4⋅r² ⁄ sin(α)
Пример
Если у равнобедренной трапеции радиус вписанной окружности r = 5 см, а угол при основании ∠α = 30°, то её площадь:
S = 4 ⋅ 5² / sin (30) = 100 / 0.5 = 200 см²
