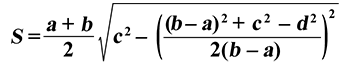{S = dfrac{1}{2} (a + b) cdot h}
Площадь трапеции можно найти множеством способов. Для вас мы собрали все возможные варианты нахождения площади. Для вашего удобства для каждой формулы создан калькулятор, который поможет рассчитать площадь трапеции по известным данным. От вас требуется только подставить значения и в режиме онлайн мгновенно получить ответ. Формулы и калькуляторы сгруппированы по типам трапеций – обычная, равнобедренная (равнобокая).
- Калькулятор площади трапеции
- Площадь трапеции
- через основания и высоту
- через среднюю линию и высоту
- через диагонали и среднюю линию
- через 4 стороны
- через диагонали и угол между ними
- через основания и углы при основании
- через площади треугольников
- через диагонали и высоту
- через радиус вписанной окружности и основания
- через перпендикулярные диагонали
- Площадь равнобедренной (равнобокой) трапеции
- через основания и высоту
- через 3 стороны (формула Брахмагупты)
- через верхнее основание, боковую сторону и угол при нижнем основании
- через нижнее основание, боковую сторону и угол при нижнем основании
- через основания и угол
- через диагонали и угол между ними
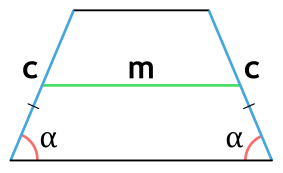
- через боковую сторону, угол при основании и среднюю линию
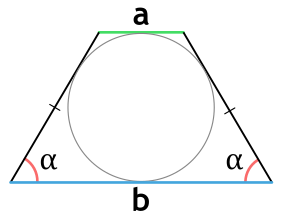
- через радиус вписанной окружности и угол при основании
- Площадь равнобедренной (равнобокой) трапеции, в которую можно вписать окружность
- через высоту (диаметр вписанной окружности) и угол при основании
- через основания и угол при основании
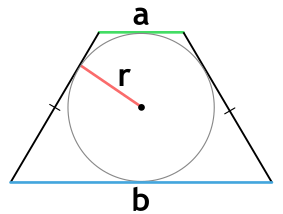
- через основания и радиус вписанной окружности
- через основания
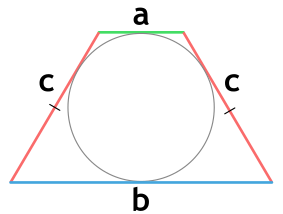
- через основания и боковую сторону
- через основания и среднюю линию
- Примеры задач
Площадь трапеции
Трапеция — выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
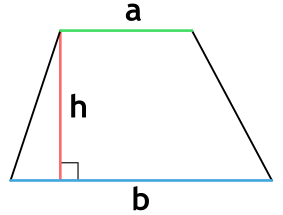
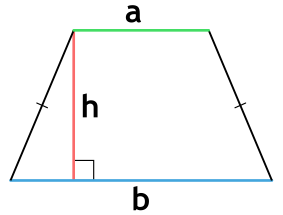
Площадь трапеции через основания и высоту
{S = dfrac{1}{2} (a + b) cdot h}
a и b – основания трапеции
h – высота, проведенная к основанию
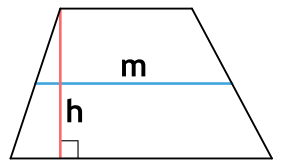
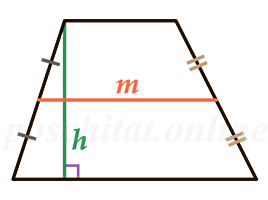
Площадь трапеции через среднюю линию и высоту
{S = m cdot h}
m – средняя линия трапеции
h – высота трапеции
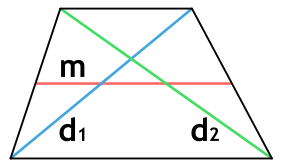
Площадь трапеции через диагонали и среднюю линию
{S = sqrt{p(p-d_1)(p-d_2)(p-2m)}}
{p = dfrac{d_1+d_2+2m}{2}}
d1 и d2 – диагонали трапеции
m – средняя линия трапеции
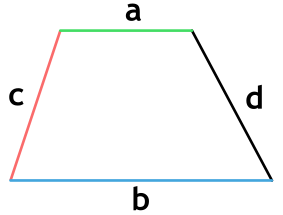
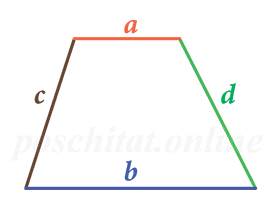
Площадь трапеции через 4 стороны
{S = dfrac{a+b}{2} sqrt{c^2 – {Big( dfrac{(a-b)^2 + c^2 – d^2}{2(a-b)} Big)}^2}}
a, b, c и d – стороны трапеции
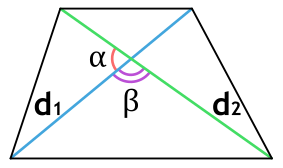
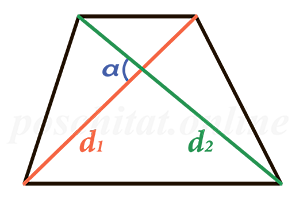
Площадь трапеции через диагонали и угол между ними
{S = dfrac{d_1 cdot d_2}{2}cdot sin(alpha); S = dfrac{d_1 cdot d_2}{2}cdot sin(beta)}
d1 и d2 – диагонали трапеции
α или β – угол между диагоналями трапеции
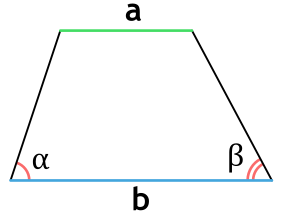
Площадь трапеции через основания и углы при основании
{S = dfrac{b^2 – a^2}{2} cdot dfrac{sin(alpha) cdot sin(beta)}{sin(alpha + beta)}}
a и b – основания трапеции
α или β – прилежащие к основанию трапеции углы
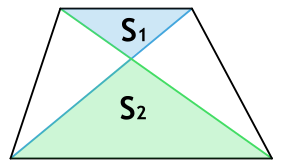
Площадь трапеции через площади треугольников
{S = (sqrt{S_1} + sqrt{S_2})^2}
S1 и S2 – площади образованных пересечением диагоналей трапеции треугольников
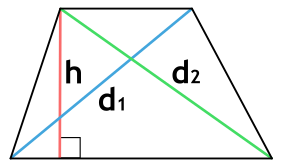
Площадь трапеции через диагонали и высоту
{S = dfrac{sqrt{{d_2}^2-h^2}+sqrt{{d_1}^2-h^2}}{2} cdot h}
d1 и d2 – диагонали трапеции
h – высота трапеции
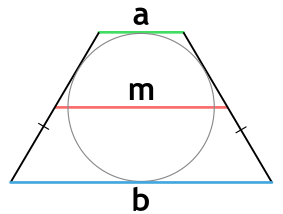
Площадь трапеции через радиус вписанной окружности и основания
{S = (a+b)cdot r}
a и b – основания трапеции
r – радиус вписанной в трапецию окружности
Площадь трапеции через перпендикулярные диагонали
{S = dfrac{1}{2} cdot d_1 cdot d_2}
d1 и d2 – перпендикулярные диагонали трапеции
Площадь равнобедренной (равнобокой) трапеции
Равнобедренная трапеция — это трапеция, у которой боковые стороны равны.
Площадь равнобедренной трапеции через основания и высоту
{S = dfrac{a+b}{2} cdot h}
a и b – основания равнобедренной трапеции
h – высота, проведенная к основанию равнобедренной трапеции
Площадь равнобедренной трапеции через 3 стороны (формула Брахмагупты)
{S = sqrt{(p-a)(p-b)(p-c)^2}}
{p = dfrac{a+b+2c}{2}}
a и b – основания равнобедренной трапеции
c – боковая сторона равнобедренной трапеции
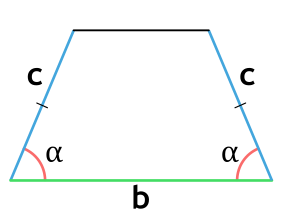
Площадь равнобедренной трапеции через верхнее основание, боковую сторону и угол при нижнем основании
{S = c cdot sin(alpha) cdot (a+c cdot cos(alpha))}
a – верхнее основание равнобедренной трапеции
c – боковая сторона равнобедренной трапеции
α – прилежащие к нижнему основанию трапеции углы
Площадь равнобедренной трапеции через нижнее основание, боковую сторону и угол при нижнем основании
{S = c cdot sin(alpha) cdot (b-c cdot cos(alpha))}
b – нижнее основание равнобедренной трапеции
c – боковая сторона равнобедренной трапеции
α – прилежащий к нижнему основанию трапеции угол
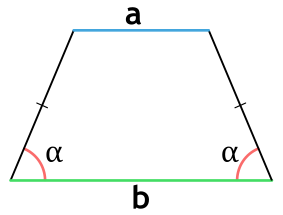
Площадь равнобедренной трапеции через основания и угол
{S = dfrac{1}{2}(b^2-a^2) cdot tg(alpha)}
a и b – основания равнобедренной трапеции
α – прилежащий к основанию трапеции угол
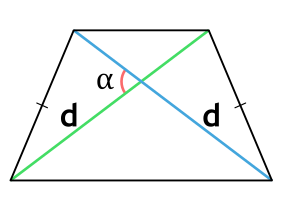
Площадь равнобедренной трапеции через диагонали и угол между ними
{S = dfrac{1}{2}d^2 cdot sin(alpha)}
a – диагональ равнобедренной трапеции
α – угол между диагоналями равнобедренной трапеции
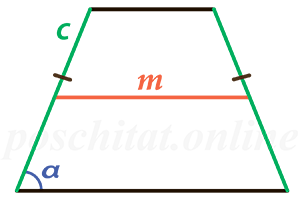
Площадь равнобедренной трапеции через боковую сторону, угол при основании и среднюю линию
{S = m cdot c cdot sin(alpha)}
m – средняя линия равнобедренной трапеции
c – боковая сторона равнобедренной трапеции
α – угол при основании равнобедренной трапеции
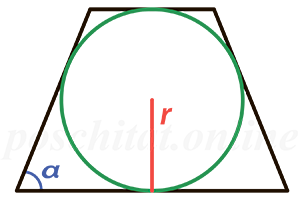
Площадь равнобедренной трапеции через радиус вписанной окружности и угол при основании
{S = dfrac{4r^2}{sin(alpha)}}
r – радиус вписанной окружности
α – угол при основании равнобедренной трапеции
Площадь равнобедренной (равнобокой) трапеции, в которую можно вписать окружность
В трапецию можно вписать окружность тогда и только тогда, когда суммы ее противоположных сторон равны.
Площадь равнобедренной трапеции, в которую можно вписать окружность, через высоту (диаметр вписанной окружности) и угол при основании
{S = dfrac{h^2}{sin(alpha)}}
h – высота равнобедренной трапеции
α – угол при основании равнобедренной трапеции
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и угол при основании
{S = dfrac{a cdot b}{sin(alpha)}}
a и b – основания равнобедренной трапеции
α – угол при основании равнобедренной трапеции
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и радиус вписанной окружности
{S = r(a+b); r=dfrac{sqrt{a cdot b}}{2}}
a и b – основания равнобедренной трапеции
r – радиус вписанной окружности
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания
{S = sqrt{a cdot b} cdot dfrac{a+b}{2}}
a и b – основания равнобедренной трапеции
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и боковую сторону
{S = c cdot sqrt{a cdot b}}
a и b – основания равнобедренной трапеции
c – боковая сторона равнобедренной трапеции
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и среднюю линию
{S = m cdot sqrt{a cdot b}}
a и b – основания равнобедренной трапеции
m – средняя линия равнобедренной трапеции
Примеры задач на нахождение площади трапеции
Задача 1
Найдите площадь трапеции, если основания равны 6см и 9 см, а высота трапеции равна 5 см.
Решение
Для решения задачи воспользуемся первой формулой.
S = dfrac{1}{2} (a + b) cdot h = dfrac{1}{2} (6 + 9) cdot 5 = dfrac{1}{2} cdot 15 cdot 5 = dfrac{1}{2} cdot 75 = 37dfrac{1}{2} : см^2
Ответ: 37.5 см²
Полученный ответ легко проверить с помощью калькулятора .
Задача 2
Найдите площадь трапеции средняя линия которой равна 18 см, а высота 9 см.
Решение
С решением этой задачи нам поможет вторая формула.
S = m cdot h = 18 cdot 9 = 162 : см^2
Ответ: 162 см²
Воспользуемся калькулятором для проверки результата.
Задача 3
Найдите площадь трапеции диагонали которой равны 10 и 8, а средняя линия равна 3.
Решение
Для решения этой задачи нам поможет третья формула.
На первом этапе вычислим p:
p = dfrac{d_1+d_2+2m}{2} = dfrac{10+8+2 cdot 3}{2} = dfrac{10+8+6}{2} = dfrac{24}{2} = 12
А теперь можно вычислить площадь трапеции:
S = sqrt{p(p-d_1)(p-d_2)(p-2m)} = sqrt{12(12-10)(12-8)(12-2 cdot 3)} = sqrt{12 cdot 2 cdot 4 cdot 6} = sqrt{576} = 24 : см^2
Ответ: 24 см²
Осталось проверить полученный ответ.
Задача 4
Найдите площадь трапеции диагонали которой равны 17 и 15, а средняя линия равна 4.
Решение
Задача похожа на ту, что мы только что решили. Поэтому повторим шаги.
На первом этапе вычислим p:
p = dfrac{d_1+d_2+2m}{2} = dfrac{17+15+ 2 cdot 4}{2} = dfrac{17+15+8}{2} = dfrac{40}{2} = 20
А теперь можно вычислить площадь трапеции:
S = sqrt{p(p-d_1)(p-d_2)(p-2m)} = sqrt{20(20-17)(20-15)(20-2 cdot 4)} = sqrt{20 cdot 3 cdot 5 cdot 12} = sqrt{3600} = 60 : см^2
Ответ: 60 см²
Проверка .
Задача 5
Найдите площадь трапеции диагонали которой равны 8 и 6 а средняя линия равна 5.
Решение
Еще одна типовая задача. Повторим действия как в задачах выше.
На первом этапе вычислим p:
p = dfrac{d_1+d_2+2m}{2} = dfrac{8+6+ 2 cdot 5}{2} = dfrac{8+6+10}{2} = dfrac{24}{2} = 12
А теперь можно вычислить площадь трапеции:
S = sqrt{p(p-d_1)(p-d_2)(p-2m)} = sqrt{12(12-8)(12-6)(12-2 cdot 5)} = sqrt{12 cdot 4 cdot 6 cdot 2} = sqrt{576} = 24 : см^2
Ответ: 24 см²
Проверка .
Задача 6
Найдите площадь равнобедренной трапеции если её основания равны 5 см и 17 см, а боковая сторона равна 10 см.
Решение
Для решения этой задачи используем формулу Брахмагупты.
Сначала вычислим p:
p = dfrac{a+b+2c}{2} = dfrac{5+17+2 cdot 10}{2} = dfrac{22+20}{2} = dfrac{42}{2} = 21
А теперь можно вычислить площадь трапеции:
S = sqrt{(p-a)(p-b)(p-c)^2} = sqrt{(21-5)(21-17)(21-10)^2} = sqrt{16 cdot 4 cdot 11^2} = sqrt{16 cdot 4 cdot 121} = sqrt{7744}= 88 : см^2
Ответ: 88 см²
Проверка .
Задача 7
Острый угол равнобедренной трапеции равен 45°, а основания равны 8 и 6 см. Найдите площадь трапеции.
Решение
Для решения этой задачи воспользуемся формулой.
S = dfrac{1}{2}(b^2-a^2) cdot tg(alpha) = dfrac{1}{2}(8^2-6^2) cdot tg(45°)
Тангенс 45° = 1, продолжим вычисления:
S = dfrac{1}{2}(8^2-6^2) cdot tg(45°) = dfrac{1}{2}(64-36) cdot 1 = dfrac{1}{2} cdot 28 = 14 : см^2
Ответ: 14 см²
Убедиться в правильности решения нам поможет калькулятор .
Площадь трапеции
- Главная
- /
- Математика
- /
- Геометрия
- /
- Площадь трапеции
Чтобы найти площадь трапеции воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Через длины оснований и высоту
Чему равна площадь трапеции, если:
основание a =
основание b =
высота h =
Ответ: S =
0
ед.²
Округление ответа:
Чему равна площадь трапеции если известны основания a и b, а также высота h?
Формула
S = ½ ⋅ (a + b) ⋅ h
Пример
Если у трапеции основание a = 3 см, основание b = 6 см, а высота h = 4 см, то её площадь:
S = ½ ⋅ (3 + 6) ⋅ 4 = 36 / 2 = 18 см²
Через среднюю линию и высоту
Чему равна площадь трапеции, если:
средняя линия m =
высота h =
Ответ: S =
0
ед.²
Округление ответа:
Чему равна площадь трапеции если известны средняя линия m и высота h?
Формула
S = m ⋅ h
Пример
Если у трапеции средняя линия m = 6 см, а высота h = 4 см, то её площадь:
S = 6 ⋅ 4 = 24 см²
Через длины сторон и оснований
Чему равна площадь трапеции, если:
основание a =
основание b =
сторона c = сторона d =
Ответ: S =
0
ед.²
Округление ответа:
Чему равна площадь трапеции если известны основания a и b, а также стороны c и d?
Формула
Пример
Если у трапеции основание a = 2 см, основание b = 6 см, сторона c = 4 см, а сторона d = 7 см, то её площадь:
S ≈ 13.555 см²
Через диагонали и угол между ними
Чему равна площадь трапеции, если:
диагональ d1 =
диагональ d2 =
угол α =
Ответ: S =
0
ед.²
Округление ответа:
Чему равна площадь трапеции если известны диагонали d1 и d2 и угол между ними α?
Формула
S = ½ ⋅ d1 ⋅ d2 ⋅ sin(α)
Пример
Если у трапеции одна диагональ d1 = 5 см, другая диагональ d2 = 7 см, а угол между ними ∠α = 30°, то её площадь:
S = ½ ⋅ 5 ⋅ 7 ⋅ sin (30) = 17.5 ⋅ 0.5= 8.75 см²
Площадь равнобедренной трапеции
Через среднюю линию, боковую сторону и угол при основании
Чему равна площадь трапеции, если:
средняя линия m =
сторона c =
угол α =
Ответ: S =
0
ед.²
Округление ответа:
Чему равна площадь равнобедренной трапеции если средняя линия m, боковая сторона с, a угол при основании α?
Формула
S = m ⋅ c ⋅ sin(α)
Пример
Если у равнобедренной трапеции средняя линия m = 6 см, сторона c = 4 см, а угол при основании ∠α = 30°, то её площадь:
S = 6 ⋅ 4 ⋅ sin (30) = 24 ⋅ 0.5 = 12 см²
Через радиус вписанной окружности
Чему равна площадь трапеции, если:
радиус r =
угол α =
Ответ: S =
0
ед.²
Округление ответа:
Чему равна площадь равнобедренной трапеции если радиус вписанной окружности r, a угол при основании α?
Формула
S = 4⋅r² ⁄ sin(α)
Пример
Если у равнобедренной трапеции радиус вписанной окружности r = 5 см, а угол при основании ∠α = 30°, то её площадь:
S = 4 ⋅ 5² / sin (30) = 100 / 0.5 = 200 см²
См. также
Выбирайте формулу в зависимости от известных величин.
1. Как найти площадь трапеции через основания и высоту
Посчитайте сумму оснований трапеции.
Умножьте результат на высоту и поделите на два.
- S – искомая площадь трапеции.
- a и b – основания трапеции (её параллельные стороны).
- h – высота трапеции.
2. Как вычислить площадь трапеции через высоту и среднюю линию
Просто умножьте высоту трапеции на среднюю линию.
- S – искомая площадь трапеции.
- m – средняя линия трапеции (отрезок, соединяющий середины боковых сторон).
- h – высота трапеции.
3. Как найти площадь трапеции через диагонали и угол между ними
Умножьте одну диагональ на другую, а затем — на синус любого угла между ними.
Поделите результат на два.
- S – искомая площадь трапеции.
- x и y – диагонали трапеции.
- α – любой угол между диагоналями.
4. Как найти площадь трапеции через четыре стороны
Отнимите от большего основания меньшее.
Найдите квадрат полученного числа.
Прибавьте к результату квадрат одной боковой стороны и отнимите квадрат второй.
Поделите полученное число на удвоенную разность оснований.
Найдите квадрат результата и отнимите его от квадрата боковой стороны.
Найдите корень из полученного числа.
Умножьте результат на половину от суммы оснований.
- S – искомая площадь трапеции.
- a, b – основания трапеции.
- c, d – боковые стороны.
5. Как вычислить площадь равнобедренной трапеции через четыре стороны
Отнимите от большего основания трапеции меньшее и поделите результат на два.
Найдите квадрат полученного числа и отнимите его от квадрата боковой стороны.
Найдите корень из результата.
Умножьте полученное число на сумму оснований и поделите на два.
- S — искомая площадь трапеции.
- a, b — основания трапеции.
- c, d — боковые стороны (напомним, в равнобедренной трапеции они равны).
6. Как найти площадь равнобедренной трапеции через радиус вписанной окружности и угол
Найдите квадрат радиуса и умножьте его на четыре.
Поделите результат на синус известного угла.
- r — радиус вписанной окружности.
- α — любой угол трапеции.
Читайте также 📐✏️🎓
- 8 способов найти длину окружности
- 8 способов найти периметр треугольника
- 7 способов найти площадь прямоугольника
- Как перевести обычную дробь в десятичную
- Как освоить устный счёт школьникам и взрослым
Трапеция — это четырехугольник, в котором две противоположные стороны параллельны.
Онлайн-калькулятор площади трапеции
Введем некоторые понятия, которые в дальнейшем помогут решить задачи, связанные с нахождением площади данной фигуры.
Основания трапеции — это стороны, параллельные друг другу.
Боковые стороны — соответственно, две оставшиеся стороны.
Средняя линия — отрезок, который соединяет центры боковых сторон. Эта линия всегда параллельна основаниям трапеции.
Виды трапеций
Трапеция бывает трех видов:
- Равнобедренная – та, у которой боковые стороны равны.
- Прямоугольная, у которой два углы прямые, т. е. равны 90 градусам.
- Произвольная, которая не относится к двум вышеописанным категориям.
Площадь трапеции можно найти различными способами. Разберем их более подробно и закрепим материал решением простых задач.
Формула площади трапеции по основанию и высоте
Пусть нам дана произвольная трапеция. Чтобы найти ее площадь, воспользуемся следующей формулой:
S=a+b2⋅hS=frac{a+b}{2}cdot h
a,ba, b — основания трапеции;
hh — высота трапеции.
Найти площадь SS трапеции, в которой известны основания, численно равные 10 (см.) и 8 (см.) и высота, длиной 6 (см.).
Решение
a=8a=8
b=10b=10
h=6h=6
Сразу подставляем числа в имеющуюся у нас формулу и вычисляем искомую величину:
S=a+b2⋅h=8+102⋅6=54S=frac{a+b}{2}cdot h=frac{8+10}{2}cdot 6=54 (см. кв.)
Ответ: 54 см. кв.
Формула площади трапеции по основанию и средней линии
Нужно упомянуть, что средняя линия трапеции равна половине суммы ее оснований. Тем самым, способ нахождения площади через среднюю линию есть не что иное, как способ, аналогичный первому. Поскольку:
l=a+b2,l=frac{a+b}{2},
то:
S=l⋅hS=lcdot h
ll — средняя линия трапеции;
hh — высота.
Найти площадь трапеции, если известно, что средняя линия равна 5 (см.), а высота трапеции в 2 раза больше её.
Решение
l=5l=5
h=2⋅lh=2cdot l
Найдем высоту трапеции:
h=2⋅5=10h=2cdot 5=10
Площадь:
S=l⋅h=5⋅10=50S=lcdot h=5cdot 10=50 (см. кв.)
Ответ: 50 см. кв.
Формула площади трапеции по всем сторонам
Данный способ подходит для тех случаев, когда в задаче известны все 4 стороны нашей трапеции.
S=a+b2c2−((b−a)2+c2−d22⋅(b−a))2S=frac{a+b}{2}sqrt{c^2-big(frac{(b-a)^2+c^2-d^2}{2cdot(b-a)}big)^2}
Даны длины всех сторон трапеции. Основания равны 10 (см.) и 5 (см.), боковые стороны: 4 (см.) и 3 (см.). Найти площадь фигуры.
Решение
a=5a=5
b=10b=10
c=4c=4
d=3d=3
Тогда:
S=a+b2c2−((b−a)2+c2−d22⋅(b−a))2=15216−(25+16−910)2=18S=frac{a+b}{2}sqrt{c^2-big(frac{(b-a)^2+c^2-d^2}{2cdot(b-a)}big)^2}=frac{15}{2}sqrt{16-big(frac{25+16-9}{10}big)^2}=18 (см. кв.)
Ответ: 18 см. кв.
Формула площади трапеции через диагонали и угол между ними
S=12⋅d1⋅d2⋅sin(α)S=frac{1}{2}cdot d_1cdot d_2cdotsin(alpha)
d1,d2d_1, d_2 — диагонали трапеции;
αalpha — угол между диагоналями.
Пусть две диагонали трапеции равны 20 (см.) и 7 (см.) и при пересечении они образуют угол 30 градусов. Найти площадь трапеции SS.
Решение
d1=20d_1=20
d2=7d_2=7
α=30∘alpha=30^{circ}
Площадь:
S=12⋅d1⋅d2⋅sin(α)=12⋅20⋅7⋅sin(30∘)=35S=frac{1}{2}cdot d_1cdot d_2cdotsin(alpha)=frac{1}{2}cdot20cdot 7cdotsin(30^{circ})=35 (см. кв.)
Ответ: 35 см. кв.
Формула площади трапеции через радиус вписанной окружности и угол
Этот случай подходит только для равнобедренной трапеции.
S=4⋅r2sin(α)S=frac{4cdot r^2}{sin(alpha)}
rr — радиус вписанной окружности;
αalpha — угол между основанием и боковой стороной.
Дан радиус вписанной окружности в трапецию, равный 4 (см.). Угол αalpha равный 90 градусам. Найти площадь трапеции.
Решение
r=4r=4
α=90∘alpha=90^{circ}
По формуле:
S=4⋅r2sin(α)=4⋅16=64S=frac{4cdot r^2}{sin(alpha)}=4cdot 16=64 (см. кв.)
Ответ: 64 см. кв.
Хотите заказать контрольную работу по геометрии? У нас самые низкие цены среди конкурентов!
Тест по теме «Площадь трапеции»
Трапеция – это четырехугольник, у которого две стороны параллельны друг другу. Высотой трапеции называют линию, перпендикулярную основаниями, для удобства ее часто проводят из тупого угла трапеции на большее основание. Средняя линия трапеции – это линия, которая параллельна основаниям, и разделяет боковые стороны ровно пополам. Среднюю линию трапеции можно найти средним арифметическим оснований – сложив их и разделив на два.
Площадь трапеции в самом простом виде – это произведение средней линии на высоту, или если раскрыть формулу средней линии, то произведение полусуммы оснований на высоту.
Доказательством этой формулы будет служить представление площади трапеции, как суммы площадей двух треугольников полученных при проведении диагонали.
Площади этих треугольников будут равны соответственно 

Вывести формулу, для того чтобы вычислить площадь трапеции через стороны, можно с помощью метода подстановки.
Проведя две высоты в трапеции, получаем по бокам прямоугольные треугольники с известными гипотенузами и неизвестными катетами x и y.
Таким образом x+y=d-b, y=d-b-x.
Одинаковый катет у обоих треугольников – высота, которую мы ищем. Через теорему Пифагора в прямоугольных треугольниках выражаем высоту 

x2-(d-b-x)2=a2-c2 – Подставляем вместо х полученное выше выражение d-b-y.
x2-d2+bd+dx-b2+bd-bx-x2+dx-bx=a2-c2 – Раскрываем скобки.
x2-d2+2bd+2dx-b2-2bx-x2=a2-c2 – Приводим подобные слагаемые.
2dx-2bx=a2-c2+d2+b2-2bd – Переносим все вправо, оставляя слева только y.
2x(d-b)=a2-c2+(d-b)2 – Выносим общие множители.
Подставляем обратно y в формулу высоты 
Формула площади трапеции через стороны будет выглядеть так:
Площадь трапеции через диагонали и угол между ними считается условным делением трапеции на четыре треугольника, точно также как и площадь любого произвольного четырехугольника.
Площадь равнобедренной трапеции можно найти еще одним способом, если даны угол при основании и радиус вписанной окружности. Дело в том, что центр вписанной окружности, откуда берет свое начало радиус, находится точно в центре трапеции, таким образом, приравнивая высоту и диаметр окружности (либо удвоенный радиус). Также одно из свойств трапеции, описанной вокруг окружности – это равенство суммы оснований и суммы боковых сторон, значит, мы сможем найти среднюю линию, зная боковые стороны. Проведя высоту, из прямоугольного треугольника получаем боковую сторону 
Тогда площадь трапеции равна