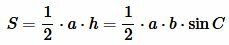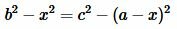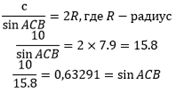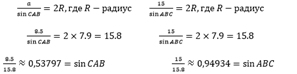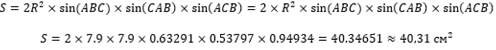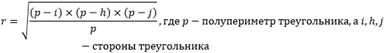Как найти площадь треугольника abc в круге - Сайт, где вы сможете решить свои вопросы

Как найти площадь треугольника

На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.

Треугольник – это многоугольник с тремя сторонами.

По формуле Герона

Формула Герона для нахождения площади треугольника:

Через основание и высоту

Формула нахождения площади треугольника с помощью половины его основания и высоту:

Через две стороны и угол

Формула нахождения площади треугольника через две стороны и угол между ними:

Через сторону и два прилежащих угла

Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:

Площадь прямоугольного треугольника

Прямоугольный треугольник – треугольник у которого один из углов прямой, т.е. равен 90°.

Формула нахождения площади прямоугольного треугольника через катеты:

Площадь равнобедренного треугольника через стороны

Равнобедренный треугольник – треугольник, в котором две стороны равны. А значит, равны и два угла.

Формула нахождения площади равнобедренного треугольника через две стороны:

Площадь равнобедренного треугольника через основание и угол

Формула нахождения площади равнобедренного треугольника через основание и угол:

Площадь равностороннего треугольника через стороны

Равносторонний треугольник – треугольник, в котором все стороны равны, а каждый угол равен 60°.

Формула нахождения площади равностороннего треугольника через сторону:

Площадь равностороннего треугольника через высоту

Формула нахождения площади равностороннего треугольника через высоту:

Площадь равностороннего треугольника через радиус вписанной окружности

Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:

Площадь равностороннего треугольника через радиус описанной окружности

Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:

Площадь треугольника через радиус описанной окружности и три стороны

Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:

Площадь треугольника через радиус вписанной окружности и три стороны

Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:

Найти площадь треугольника абс в окружности

В треугольнике ABC угол С равен 90°, радиус вписанной окружности равен 2. Найдите площадь треугольника ABC, если AB = 12.

Пусть A₁, B₁ и C₁ — точки касания вписанной окружности со сторонами BC, AC и AB соответственно. Радиус вписанной окружности обозначим r. Тогда AC₁ = AB₁, BC₁ = BA₁ и CA₁ = CB₁ = r. Периметр треугольника ABC равен

а его полупериметр p равен AB + r.

По формуле площади треугольника находим

Площадь треугольника онлайн

С помощю этого онлайн калькулятора можно найти площадь треугольника. Для нахождения площади треугольника введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть смотрите ниже.

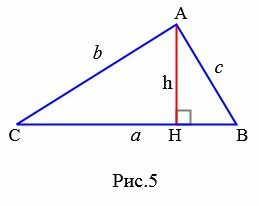
Площадь треугольника по основанию и высоте

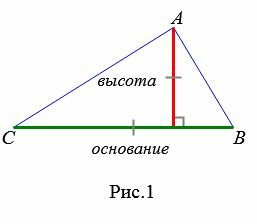
Любой из сторон треугольника можно называть основанием треугольника. Если основание выбрана, то под словом “высота” понимают высоту треугольника, проведенную к основанию (Рис.1):

Теорема 1. Площадь треугольника равна половине произведения его основания на высоту.

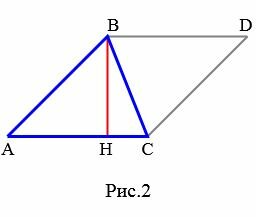
Доказательство. Пусть AC основание треугольника ABC (Рис.2).

Проведем высоту BH. Обозначим через S площадь треугольника. Докажем, что

( small S= frac <large 1> <large 2>cdot AC cdot BH. )

Из вершины B проведем прямую, параллельную стороне AC, а из C − прямую, параллельную стороне AB. Поскольку ( small AC || BD ) и ( small AB || CD ), то ABDC является параллелограммой и, следовательно, ( small AC = BD ), ( small AB = CD . ) Тогда треугольники ABC и BCD равны по трем сторонам (см. статью на странице Треугольники. Признаки равенства треугольников). Так как площадь параллелограмма ABDC равна ( small S_=AC cdot BH, ) то площадь треугольника ABC (и BCD)равна половине площади параллелограмма:

Следствие 1. Если высоты треугольников равны, то их площади относятся как основания.

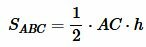
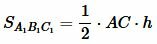
Обозначим через k отношение

( small k= frac <large AC><large A_1C_1>. )

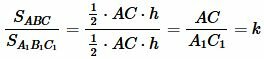
То есть отношение площадей треугольников с равными высотами равно отношению их оснований.

Следствие 2. Площадь прямоугольного треугольника равна половине произведения его катетов.

Действительно. Поскольку в прямоугольном треугольнике катеты перпендикулярны друг другу, то один из них можно определить как основание, а другой − как высоту. Тогда по теореме 1, площадь прямоугольного треугольника равна половине произведения его катетов.

Площадь треугольника по двум сторонам и углу между ними

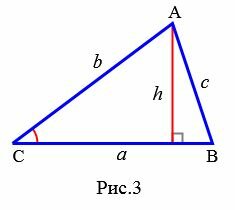
Теорема 2. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

Доказательство. Обозначим через S площадь треугольника ABC и пусть a=BC, b=AC (Рис.3). Докажем, что

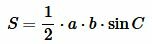
Площадь данного треугольника можно вычислить по формуле, полученной выше (теорема 1):

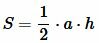(1)

где h − высота треугольника.

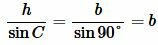
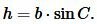(2)

Подставляя (2) в (1), получим:

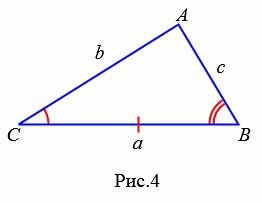
Площадь треугольника по стороне и прилежащим двум углам

Пусть известна сторона треугольника и две прилежащие углы (Рис.4).

Найдем формулу площади этого треугольника. Обозначим через S площадь треугольника. Если у треугольника известны два угла, то можно найти и третий угол:

(4)

Найдем сторону b используя теорему синусов:

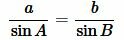
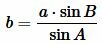(5)

В предыдующем параграфе мы вывели площадь треугольника по двум сторонам и углу между ними. Подставляя (4) и (5) в (3), получим:

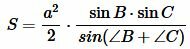(6)

Площадь треугольника по трем сторонам. Формула Герона

Для нахождения площади треугольника по трем сторонам используют формулу Герона:

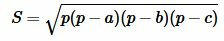(7)

где a, b, c − стороны треугольника, а p − полупериод треугольника:

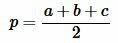
Доказательство формулы Герона. На рисунке 5 треугольник ABC имеет стороны a=BC, b=AC, c=AB. Проведем высоту h=AH. Обозначим x=CH. Тогда BH=a−x. Применим теорему Пифагора для треугольников AHC и AHB:

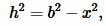(8)

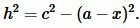(9)

Из (8) и (9) следует:

Откуда находим x:

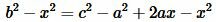
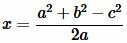(10)

Подставляя (10) в (8) найдем h:

Тогда площадь треугольника равна:

Преобразовав (12) получим формулу (7):

Площадь треугольника по трем сторонам и радусу описанной окружности

Пусть известны все три стороны треугольника и радиус описанной окружности (Рис.6). Докажем, что площадь треугольника равна: ( small S=frac<large abc><large 4R>. )

[spoiler title=”источники:”]

http://oge.sdamgia.ru/test?pid=311924

http://matworld.ru/geometry/ploshchad-treugolnika.php

[/spoiler]

Источник

Как найти площадь треугольника через радиус описанной окружности?

Площадь треугольника равна частному от деления произведения сторон треугольника на четыре радиуса описанной около треугольника окружности.

Формула для нахождения площади треугольника через радиус описанной окружности:

$[S = frac{{abc}}{{4R}}]$

Дано: ∆ ABC,

окружность (O; R) — описанная,

AB=c, BC=a, AC=b.

Доказать:

$[{S_{Delta ABC}} = frac{{abc}}{{4R}}]$

Доказательство:

1) Обозначим ∠A=α.

Площадь треугольника ABC

по двум сторонам и углу между ними

равна

$[{S_{Delta ABC}} = frac{1}{2}AC cdot AB cdot sin angle A = frac{1}{2}bcsin alpha .]$

2) По следствию из теоремы синусов,

$[R = frac{a}{{2sin alpha }}.]$

Выразим из этой формулы синус альфа

$[sin alpha = frac{a}{{2R}}]$

и подставим полученное выражение в первую формулу

$[{S_{Delta ABC}} = frac{1}{2}bcsin alpha = frac{1}{2}bc cdot frac{a}{{2R}} = frac{{abc}}{{4R}}.]$

Что и требовалось доказать.

Источник

Площадь треугольника через радиус описанной окружности

Как найти площадь треугольника через радиус описанной окружности

Описанной около выпуклого многоугольника окружностью называют такую окружность, которая пересекает каждую из вершин рассматриваемого многоугольника.

Если около некоторого многоугольника описана окружность, то данный многоугольник является вписанным в эту окружность. Существует правило, согласно которому в выпуклый многоугольник можно также вписать какую-либо окружность. Для этого требуется, чтобы все серединные перпендикуляры сторонам многоугольника обладали единственной точкой пересечения. Данную точку называют центром вписанной в многоугольник окружности.

Центр окружности, которая описана около многоугольника, расположен на одинаковом расстоянии от всех вершин рассматриваемого многоугольника. При этом отрезок, один конец которого совпадает с центром окружности, а второй — с любой из вершин многоугольника, равен радиусу описанной окружности.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Пример

Рассмотрим наглядный пример:

Источник: treugolniki.ru

На рисунке изображен многоугольник с пятью углами ABCDE. Около этого пятиугольника описана окружность, центр которой обозначен О, а радиус равен R. Таким образом, ABCDE представляет собой вписанный пятиугольник, а O является точкой, в которой пересекаются серединные перпендикуляры, проведенные к сторонам ABCD. Запишем следующие соотношения:

(AP = PE,OP bot AE)

(AM = MB,OM bot AB)

(BN = NC,ON bot BC)

(CL = LD,OL bot CD)

(DK = KE,OK bot DE)

Заметим, что точка O находится на одинаковом расстоянии, то есть равноудалена, от каждой из вершин рассматриваемого многоугольника с каким-то периметром:

Источник: treugolniki.ru

Данное расстояние между точкой О и какой-либо вершиной соответствует радиусу описанной окружности:

OA=OB=OC=OD=OE=R

Примечание

Окружность можно описать около любого треугольника. А, к примеру, около выпуклого четырехугольника имеется возможность описать окружность только в том случае, если противолежащие углы данной геометрической фигуры в сумме дают 180°.

Если имеется некий правильный многоугольник, то есть равносторонний, вокруг него можно описать окружность. Также в какой-либо правильный многоугольник представляется возможным вписать окружность. В данном случае центры вписанной и описанной окружности совпадают с центром правильного многоугольника.

Отсутствует стандартная формула, с помощью которой можно определить радиус окружности, описанной около многоугольника. Подобная формула предусмотрена для вычисления радиуса вписанной окружности. Поэтому радиус описанной окружности соответствует радиусу окружности, которая описана около какого-либо из треугольников с вершинами, являющимися вершинами описанного многоугольника.

К примеру, представим, что имеется некий многоугольник ABCDE с пятью углами, около которого описана окружность. Радиус данной окружности равен радиусу окружности, описанной около какого-либо из перечисленных треугольников:

ABC;
ABD;
ABE;
BCD;
BCE;
ACD;
ADE и так далее.

Частные случаи составления формул для расчета радиуса описанной окружности:

правильные многоугольники;
треугольники;
прямоугольники.

Описанная около треугольника окружность — это окружность, на которой расположены все вершины данного треугольника. В этом случае треугольник называют треугольником, вписанным в эту окружность.

Источник: treugolniki.ru

Заметим, что:

(OA=OB=OC=R)

Расстояние, на которое удалена каждая из вершин треугольника от центральной точки описанной окружности, соответствует радиусу данной окружности. Заметим, что окружность допустимо описать около какого-либо треугольника без ограничений. Описанная около треугольника окружность обладает центром, совпадающим с точкой, в котором пересекаются серединные перпендикуляры, проведенные к граням треугольника. Данные отрезки перпендикулярны относительно сторон треугольника и пересекают середины этих сторон.

Источник: treugolniki.ru

Предположим, что имеется некий треугольник с острыми углами. Если описать окружность около такой геометрической фигуры, то центр окружности будет расположен в ее внутреннем пространстве.

Источник: treugolniki.ru

Представим, что имеется некий прямоугольный треугольник. Если описать около такой геометрической фигуры окружность, то ее центр будет расположен на середине гипотенузы.

Источник: treugolniki.ru

Около треугольника с тупым углом также допустимо описать окружность. При этом центр данной окружности окажется вне геометрической фигуры. В данном случае центральная точка окружности расположена напротив тупого угла треугольника, за большей стороной.

Теорема с доказательством

Теорема

Определить площадь треугольника можно путем деления результата от произведения сторон этого треугольника на четыре радиуса окружности, которая описана около данного треугольника.

Источник: treugolniki.ru

Докажем записанную теорему. Для этого представим, что существует некий треугольник АВС. Опишем около данного треугольника окружность (O; R). Обозначим стороны треугольника таким образом:

(AB=c, BC=a, AC=b.)

Нужно представить доказательство того, что:

({S_{Delta ABC}} = frac{{abc}}{{4R}})

Изобразим данные треугольник и окружность для наглядности:

Источник: treugolniki.ru

Ведем обозначение угла А. Пусть:

(angle A= alpha)

Вспомним, что вычислить площадь треугольника можно по двум сторонам и углу между ними, как половину от результата умножения пары сторон треугольника на синус угла, расположенного между ними.

Формула 1

Формула имеет вид:

(S = frac{1}{2}absin alpha)

Источник: treugolniki.ru

Применительно к нашему случаю, получим:

({S_{Delta ABC}} = frac{1}{2}AC cdot AB cdot sin angle A = frac{1}{2}bcsin alpha.)

Далее требуется воспользоваться теоремой синусов, вернее, ее следствием. Заметим, что стороны треугольника относятся к синусу противолежащего угла, как радиус, описанной окружности около данного треугольника, умноженный на два:

(frac{a}{{sin alpha }} = frac{b}{{sin beta }} = frac{c}{{sin gamma }} = 2R)

Тогда:

(R = frac{a}{{2sin alpha }}.)

С помощью данной формулы можно представить расчет синуса угла (alpha):

(sin alpha = frac{a}{{2R}})

При подстановке полученного выражения в начальную формулу имеем:

({S_{Delta ABC}} = frac{1}{2}bcsin alpha = frac{1}{2}bc cdot frac{a}{{2R}} = frac{{abc}}{{4R}}.)

Теорема доказана.

Примеры задач

Ранее получилось доказать теорему о площади треугольника, вычисляемой с помощью радиуса описанной окружности. Запишем формулу, отражающую смысл этой теоремы:

(S = frac{{abc}}{{4R}})

Используя данную формулу, можно решать задачи по геометрии. Приведем несколько типичных примеров таких заданий.

Задача 1

Дан равнобедренный треугольник с боковыми гранями, равными 50. Основание фигуры составляет 80. Требуется определить радиус, которым обладает описанная около данного треугольника окружность.

Решение

Найдем радиус окружности через площадь треугольника:

(R=frac{abc}{4S})

С помощью формулы Герона рассчитаем площадь:

(S=sqrt{p(p-a)(p-b)(p-c)}=sqrt{90(90-50)^2(90-80)}=900)

В результате:

(R=frac{90cdot 50cdot 50}{4cdot 900}=62,5)

Ответ: 62,5.

Задача 2

Имеется некий треугольник АВС. Одна из его сторон АВ составляет 28. Угол напротив этой стороны С составляет 150 градусов. Требуется определить радиус окружности, которая описана около данного треугольника.

Решение

Воспользуемся теоремой синусов и запишем:

(frac{AB}{sinC}=2R)

(frac{28}{sin150^{circ}}=2R)

(frac{28}{frac{1}{2}}=2R)

В результате:

R=28.

Ответ: 28.

Задача 3

Дан некий треугольник АВС. Градусная мера угла С составляет 90 градусов, а стороны равны:

BC=16;

AC=30.

Нужно вычислить, каким радиусом обладает описанная около данного треугольника окружность.

Решение

Заметим, что в условии задачи речь идет о прямоугольном треугольнике. Тогда диаметр описанной около такого треугольника окружности является гипотенузой. Запишем:

(R=frac{AB}{2})

Согласно теореме Пифагора:

(AB=sqrt{BC^2+AC^2}=sqrt{16^2+30^2}=34)

В результате:

(R=frac{AB}{2}=frac{34}{2}=17)

Ответ: 17.

Задача 4

Около некого правильного треугольника описана окружность с радиусом (17sqrt{3}). Нужно вычислить сторону данного треугольника.

Решение

Согласно теореме косинусов:

( frac{AB}{sinC}=2R)

(frac{AB}{sin60^{circ}}=2cdot 17sqrt{3})

(frac{AB}{frac{sqrt3}{2}}=34sqrt{3})

В таком случае:

AB=51

Ответ: 51.

Задача 5

Имеется некий правильный треугольник, сторона которого равна (7sqrt3). Требуется вычислить радиус окружности, описанной около этой геометрической фигуры.

Решение

Согласно теореме синусов:

(frac{AB}{sinC}=2R)

(frac{7sqrt3}{sin60^{circ}}=2R)

14=2R

В результате:

R=7

Ответ: 7.

Задача 6

Имеется окружность, на которой расположены точки А, В, С. Эти точки образуют три дуги с градусными мерами в соотношении 1:6:11. Нужно вычислить, какую градусную меру имеет самый большой угол треугольника АВС.

Решение

Обозначим дугу АВ за переменную х. В таком случае:

BC=6x

AC=11x

Далее запишем следующее соотношение:

x+6x+11x=360

18x=360

x=20

В результате:

(breve{AC}=20^{circ}cdot 11=220^{circ})

Вспомним, что вписанный угол соответствует ½ дуги, на которую этот угол опирается. В результате:

(angle ABC=frac{220^{circ}}{2}=110^{circ})

Ответ: (110^{circ}.)

Задача 7

Даны треугольник и описанная около него окружность с радиусом 1. Одна из сторон треугольника равна (sqrt2). Требуется определить градусную меру острого угла треугольника, который расположен напротив этой стороны.

Решение

Согласно теореме синусов:

(frac{a}{sin alpha}=2R)

(frac{sqrt2}{sin alpha}=2cdot 1)

(sinalpha=frac{sqrt2}{2})

(alpha=45^{circ})

Согласно условию задачи, (alpha) является острым углом.

Ответ: (45^{circ}).

Задача 8

Углы некого четырехугольника составляют (56^{circ}) и (99^{circ}). Эта фигура вписана в окружность. Требуется определить самый большой из неизвестных углов.

Решение

Исходя из условия задачи, сделаем вывод о том, что данные углы не противоположны друг другу. В противном случае, эти углы в сумме составляли бы (180^{circ}).

При (angle A=99^{circ}), то (angle C=180^{circ}-99^{circ}=81^{circ})

При (angle B=56^{circ}), то ( angle D=180^{circ}-56^{circ}=124^{circ})

Тогда угол D является самым большим.

Ответ: (124^{circ}.)

Задача 9

Имеется четырехугольник ABCD. Вокруг него описана окружность. Градусная мера угла АВС составляет (38^{circ}), а угла CAD равна —(38^{circ}). Нужно определить угол ABD в градусах.

Решение

По условию задачи:

(angle ABC=38^{circ})

В результате, дуга ADC составит (76^{circ}.)

Также в условии дано:

(angle CAD=33^{circ})

Тогда дуга DC равна (66^{circ}.)

В итоге получим:

(breve{AD}=breve{ADC}-breve{DC}=76^{circ}-66^{circ}=10^{circ})

Таким образом:

(angle ABD=5^{circ})

Ответ: 5.

Задача 10

Имеется квадрат, около которого описана окружность с радиусом (45sqrt2). Требуется вычислить сторону квадрата.

Решение

Диаметр окружности равен диагонали BD квадрата, около которого она описана. Обозначим сторону квадрата за х. Используем теорему Пифагора и запишем:

(x^2+x^2=(90sqrt2)^2)

(2x^2=90^2cdot 2)

(x^2=90^2)

(x=90)

Ответ: 90.

Источник

Всем привет, меня зовут Андрей, это снова я!

Сегодня я хочу рассказать про треугольники, вписанные в окружность. Чаще всего окружности бывают вписанными в треугольник или описанными вокруг треугольника, но иногда могут встречаться в задачах и другие многоугольники. Задачи про окружности и треугольники могут встречаться не только на ЕГЭ, но и в любых других задачах.

Окружность считается вписанной в многоугольник, если все стороны многоугольника касаются этой окружности. Окружность будет описанной вокруг многоугольника, если она будет содержать все вершины многоугольника. В данной статье более подробно рассмотрим вариант второй – когда окружность описана вокруг треугольника.

А рассказать я хочу о том, как можно быстро и правильно нарисовать рисунок к тем задачам, которые касаются описанных окружностей. Если треугольник вписан в окружность, то окружность описана вокруг него.

Секрет первый: всегда начинать построение рисунка нужно с окружности. Если делать рисунок наоборот, начать рисовать треугольник, то будет очень сложно подобрать описанную вокруг него окружность. Желательно знать, где у этой окружности центр. Если мы имеем дело с электронными графическими редакторами и не знаем, как не только нарисовать окружность, но и точно определить ее центр – то лучше всего «скачать» готовую окружность вместе с отмеченным центром. Если же мы рисуем на бумаге циркулем, без помощи электроники – там все гораздо проще найти центр. Например, центр окружности обычно выбирается на пересечении двух линий листа в клеточку, да и игла самого циркуля часто оставляет на бумаге след.

После этого будем рисовать треугольник (ну или другой многоугольник, который нам нужен). Если окружность описана вокруг треугольника – это значит, что нам надо выбрать три точки на самой окружности. Секрет второй: если мы нарисовали окружность, а затем на ней выбрали любые три точки – вершины нашего треугольника, то наш треугольник всегда будет вписан в эту окружность. Эти точки нужно выбирать таким образом, чтобы полученная фигура максимально соответствовала всем условиям задачи. Приведем пример. Пусть надо решить задачу:

Боковые стороны равнобедренного треугольника равны 50, основание равно 60. Найдите радиус описанной окружности этого треугольника.

Хотя в условии задачи первым делом упоминается треугольник, а не окружность, мы все равно начнем построении с окружности:

Секреты треугольников, вписанных в окружность.

Затем смотрим внимательно – окружность вписана в треугольник, или наоборот: треугольник вписан в окружность. Главное – ничего не перепутать. В нашем случае, в условии сказано: «описанная окружность». А это значит, что треугольник вписан в окружность, то есть надо находить три точки на самой окружности. Кроме того, треугольник равнобедренный, а это значит, что нужно мысленно провести диаметр окружности так, чтобы одна половина окружности оказалась слева, вторая справа:

Тогда одна из вершин треугольника будет строго наверху этого мысленного диаметра, а две другие – симметрично друг другу – одна в «левой» половине окружности, вторая – в «правой». Кроме того, окружность надо делить не просто на три части, но нужно соблюсти соотношение этих частей как 5:5:6, потому что соотношение сторон треугольника равно соотношению дуг окружности, на которую он ее разделяет. Можно, конечно, разделить «на глаз», но для тех, у кого есть и время, и желание построить «точь-в-точь», я расскажу, как это сделать.

Если бы треугольник был равносторонний, мы бы разделили окружность на три одинаковые части. Это делалось бы так: сначала мы бы построили один радиус окружности, желательно на нашем «мысленном» диаметре, и построили бы два угла с вершиной в точке О – центре окружности. У этих углов был бы общий луч, или сторона – это тот радиус, который мы уже построили. Градусная мера была бы у каждого угла – 120 градусов, потому что 120 – это 360/3. Но это было бы в том случае, если бы у треугольника были равными все три стороны. А у нас две равные части, но третья чуть больше каждой из них.

Напомню, что мы хотим построить график не примерно точный, а максимально точный, нам даже придется воспользоваться транспортиром. Конкретно для нашей задачи: начнем строить вторую точку (потому что первая точка будет на самом верху нашего «мнимого» диаметра, который разделил бы наш круг строго пополам по вертикали). Вторая и третья точки будут ей симметричны друг другу и располагаться по разные стороны нашего «мнимого» диаметра. Напомню, что угол в 90 градусов отделил бы 0,25 от окружности в 360 градусов; нам же нужно разделить окружность так, чтобы одна точка ее делила в соотношении 50:160 (потому что 160 – это сумма соотношений сторон нашего треугольника: 50+50+60=160, ведь именно в этом отношении вершины треугольника разделят нашу окружность). Получается 0,3125, это 50/160.

Теперь составляем пропорцию: 1/360=0,3125/х, откуда х=360*0,3125=112,5. Это значит, что нам надо строить угол в 112,5 градусов.

Вот что должно получиться:

У нас получились не только три точки – вершины треугольника А, В и С, но и сами радиусы окружности – ОА, ОВ и ОС. В нашей ситуации 112,5 – это углы АОВ и ВОС. Можно вычислить также и угол АОС: 360-112,5-115,5=135 градусов. А это значит, что соотношение углов АОВ и АОС – это 112,5 к 135, или 225:270, или 45:54, или 5:6. Именно таким по условию задачи и является отношение боковой стороны треугольника к основанию, ведь 5:6 равно 50:60.

Но продолжим решать нашу задачу. Мы пока только очень точно построили нужные нам точки. Конечно, в реальности, возможно, и не нужна такая точность, но желательно иметь на графике такие фигуры, которые очень похожи на те, о которых говорится в условии задачи. Но если есть и время, и желание, и отменный педантизм – то вполне можно построить не просто очень похожие фигуры, а именно точь-в-точь такие, о которых говорится в условии задачи.

Теперь построим треугольник АВС:

Теперь несколько слов о решении этой конкретной задачи. Всего несколько слов, потому что главная цель этой статьи была в том, чтобы показать, что треугольник, вписанный в окружность, лучше всего начинать рисовать с окружности. Повторюсь, потому что эта информация очень важна. Если бы мы вначале нарисовали треугольник, было бы гораздо сложнее подобрать ту окружность, которая проходила бы через все его вершины. Но если мы вначале построим окружность, затем на этой окружности выберем три нужные нам точки – которые будут вершинами треугольника – то при таком построении окружность будет всегда будет описана вокруг этого треугольника, а треугольник будет в нее вписан. Аналогичную задачу, связанную с окружностью, вписанной в треугольник, мы рассмотрим в одной из следующий статей.

Кстати, о нашем треугольнике. Поскольку известны все три стороны треугольника, то сначала вычислим его площадь по формуле Герона:

Вначале вычислим полупериметр треугольника: ½(50+50+60)= ½*160=80;

затем вычислим площадь этого треугольника по формуле Герона:

Это можно вычислить даже без калькулятора. Под корнем – квадрат числа 30, умноженный на 1600 (потому что 1600 – это 80*20), а 1600 – это 40 в квадрате. Следовательно, при извлечении корня мы получим: 40*30 = 1200 (условных единиц – потому что нам не известны единицы при исходных цифрах, про них ничего не сказано в условии задачи).

Далее нужно воспользоваться той формулой, которая связывает площадь треугольника и радиус описанной окружности:

Здесь a, b, c – стороны треугольника, S – его площадь, R – радиус описанной окружности. Можно записать эту формулу по-другому: abc=4SR. Поскольку у нас известно всё, кроме радиуса, то запишем эту формулу по-другому:

Теперь у нас есть все данные для вычислений. В числителе: 50*50*60=150000, в знаменателе: 4*1200=4800. Делим 150000 на 4800, получаем 31,25 (условных единиц). Именно условных единиц, ведь в задании не было никаких конкретных единиц измерения.

Ответ: 31,25.

Кстати, эту же задачу можно решить и вторым способом. Второй способ будет не самый быстрый и не самый правильный, но им можно воспользоваться в крайнем случае, если вдруг позабылась формула взаимосвязи радиуса описанной окружности и площади треугольника.

Вначале, как и при первом способе, вычислим площадь треугольника по площади Герона – это будет 1200 у.е., подробности вычисления есть в этой статье.

Затем рисуем высоту ВН (перпендикуляр к стороне АС):

Площадь треугольника АВС – это половина произведения стороны АС и высоты ВН. поскольку вся площадь треугольника АВС – это 1200, то то значит, что ВН*АС=1200*2=2400. АС известно и рано 60, это значит, что ВН = 2400/60=40 (у.е.). Это значит, что R+ОН = 40, то есть: ОН = 40-R.

Но у нас есть также прямоугольный треугольник АОН, в котором АО, или R, это гипотенуза; один катет – это ОН (мы уже знаем, что ОН равно 40 – R), второй катет – АН – равен 30, потому что в равнобедренном треугольнике АВС высота ВН также является и медианой, и биссектрисой. Нам в данной ситуации важно именно то, что ВН – это медиана, а это значит, что АН = 30.

Итак, мы имеем систему из двух уравнений. Пусть ОН – это х, а АО – это R.

Поскольку в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов, то вот каким будет одно из двух уравнений нашей системы:

Второе уравнение системы простое: х=40-R, это мы уже недавно вычислили.

Подставим в первое уравнение 40-R вместо х. Вот что получится:

Раскроем скобки:

Дальнейшее ясно: 80R=900+1600, откуда R=(900+1600)/80, или R=2500/80.

И снова мы получаем 31,25!

Ответ: 31,25.

На этом пока всё, подписывайтесь на мой канал и до новых встреч!

Источник

В современном машиностроении используется масса элементов и запчастей, которые имеют в своей структуре как внешние окружности, так и внутренние. Самым ярким примером могут служить корпус подшипника, детали моторов, узлы ступицы и многое другое. При их изготовлении применяются не только высокотехнологичные приспособления, но и знания из геометрии, в частности информация об окружностях треугольника. Более детально с подобным знаниями познакомимся ниже….

Какая окружность вписана, а какая описана

Прежде всего вспомним, что окружностью называется бесконечное множество точек, удаленных на одинаковом расстоянии от центра. Если внутри многоугольника допускается построить окружность, которая с каждой стороной будет иметь только одну общую точку пересечения, то она будет называться вписанной. Описанной окружностью (не круг, это разные понятия) называется такое геометрическое место точек, при котором у построенной фигуры с заданным многоугольником общими точками будут только вершины многоугольника. Ознакомимся с этими двумя понятиями на более наглядном примере (см. рис 1.).

Рисунок 1. Вписанная и описанная окружности треугольника

На изображении построены две фигуры большого и малого диаметров, центры которых находятся G и I. Окружность большего значения называется описанной окр-тью Δ ABC, а малого – наоборот, вписанной в Δ ABC.

Для того чтобы описать вокруг треугольника окр-ть, требуется провести через середину каждой стороны перпендикулярную прямую (т.е. под углом 90°) – это точка пересечения, она играет ключевую роль. Именно она будет представлять собой центр описанной окружности. Перед тем как найти окружность, ее центр в треугольнике, требуется построить для каждого угла биссектрису, после чего выделить точку пересечения прямых. Она в свою очередь будет центром вписанной окр-ти, а ее радиус при любых условиях будет перпендикулярен любой из сторон.

На вопрос:«Какое количество окружностей вписанных может быть для многоугольника с тремя углами?» ответим сразу, что в любой треугольник можно вписать окружность и притом только одну. Потому что существует только одна точка пересечения всех биссектрис и одна точка пересечения перпендикуляров, исходящих из середин сторон.

Свойство окружности, которой принадлежат вершины треугольника

Описанная окружность, которая зависит от длин сторон при основании, имеет свои свойства. Укажем свойства описанной окружности:

Центр описанной окружности для прямоугольного треугольника находится на середине гипотенузы, у острого – внутри самого треугольника, а для тупоугольного – за ее пределами.
Диаметр любой описанной окр-сти равен половине отношения стороны и синуса угла, который принадлежит ей, в виде формулы можно представить следующим образом:
Зная радиус описанной окружности и значения углов, можно найти значение площади, не прибегая к использованию длин сторон, по следующей формуле:

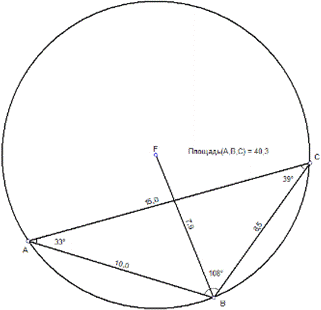
Для того чтобы более наглядно понять принцип описанной окружности, решим простую задачу. Допустим, что дан треугольник Δ ABC, стороны которого равны 10, 15 и 8,5 см. Радиус описанной окружности около треугольника (FB) составляет 7,9 см. Найти значение градусной меры каждого угла и через них площадь треугольника.

Рисунок 2. Поиск радиуса окружности через отношение сторон и синусов углов

Решение: опираясь на ранее указанную теорему синусов, найдем значение синуса каждого угла в отдельности. По условию известно, что сторона АВ равна 10 см. Вычислим значение С:

Используя значения таблицы Брадиса, узнаем, что градусная мера угла С равна 39°. Таким же методом найдем и остальные меры углов:

Откуда узнаем, что CAB = 33°, а ABC = 108°. Теперь, зная значения синусов каждого из углов и радиус, найдем площадь, подставляя найденные значения:

Ответ: площадь треугольника равна 40,31 см², а углы равны соответственно 33°, 108° и 39°.

Важно! Решая задачи подобного плана, будет нелишним всегда иметь таблицы Брадиса либо соответствующее приложение на смартфоне, так как вручную процесс может затянуться на длительное время. Также для большей экономии времени не требуется обязательно строить все три середины перпендикуляра либо три биссектрисы. Любая третья из них всегда будет пересекаться в точке пересечения первых двух. А для ортодоксального построения обычно третью дорисовывают. Может, это неправильно в вопросе алгоритма, но на ЕГЭ или других экзаменах это здорово экономит время.

Исчисление радиуса вписанной окружности

Все точки окружности одинаково удалены от ее центра на одинаковом расстоянии. Длину этого отрезка (от и до) называют радиусом. В зависимости от того, какую окр-ть мы имеем, различают два вида – внутренний и внешний. Каждый из них вычисляется по собственной формуле и имеет прямое отношение к вычислению таких параметров, как:

площадь,
градусная мера каждого угла,
длины сторон и периметр.

Рисунок 3. Расположение вписанной окружности внутри треугольника

Вычислить длину расстояния от центра до точки соприкосновения с любой из сторон можно такими способами: через стороны, высоты, боковые стороны и углы (для равнобокого треугольника).

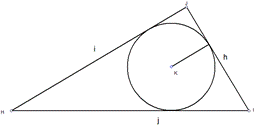
Использование полупериметра

Полупериметром называется половина суммы длин всех сторон. Такой способ считается самым популярным и универсальным, потому как независимо от того, какой тип треугольника дан по условию, он подходит для всех. Порядок вычисления имеет следующий вид:

Если дан «правильный»

Одним из малых преимуществ «идеального» треугольника является то, что вписанная и описанная окружности имеют центр в одной точке. Это удобно при построении фигур. Однако в 80% случаев ответ получается «некрасивым». Тут имеется ввиду, что очень редко радиус вписанной окр-ти будет целым натуральным числом, скорее наоборот. Для упрощенного исчисления используется формула радиуса вписанной окружности в треугольник:

Если боковины одинаковой длины

Одним из подтипов задач на гос. экзаменах будет нахождение радиуса вписанной окружности треугольника, две стороны которого равны между собой, а третья нет. В таком случае рекомендуем использовать этот алгоритм, который даст ощутимую экономию времени на поиск диаметра вписанной окр-ти. Радиус вписанной окружности в треугольник с равными «боковыми» вычисляется по формуле:

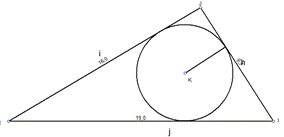
Более наглядное применение указанных формул продемонстрируем на следующей задаче. Пускай имеем треугольник (Δ HJI), в который вписана окр-ть в точке K. Длина стороны HJ = 16 см, JI = 9,5 см и сторона HI равна 19 см (рисунок 4). Найти радиус вписанной окр-ти, зная стороны.

Рисунок 4. Поиск значения радиуса вписанной окружности

Решение: для нахождения радиуса вписанной окр-ти найдем полупериметр:

Отсюда, зная механизм вычисления, узнаем следующее значение. Для этого понадобятся длины каждой из сторон (дано по условию), а также половину периметра, получается:

Отсюда следует, что искомый радиус равен 3,63 см. Согласно условию, все стороны равны, тогда искомый радиус будет равен:

При условии, если многоугольник равнобокий (например, i = h = 10 см, j = 8 см), диаметр внутренней окр-ти с центром в точке K будет равен:

В условии задачи может даваться треугольник с углом 90°, в таком случае запоминать формулу нет необходимости. Гипотенуза треугольника будет равна диаметру. Более наглядно это выглядит так:

Важно! Если задана задача на поиск внутреннего радиуса, не рекомендуем проводить вычисления через значения синусов и косинусов углов, табличное значение которых точно не известно. В случае, если иначе узнать длину невозможно, не пытайтесь «вытащить» значение из-под корня. В 40% задач полученное значение будет трансцендентным (т.е. бесконечным), а комиссия может не засчитать ответ (даже если он будет правильным) из-за его неточности или неправильной формы подачи. Особое внимание уделите тому, как может видоизменяться формула радиуса описанной окружности треугольника в зависимости от предложенных данных. Такие «заготовки» позволяют заранее «видеть» сценарий решения задачи и выбрать наиболее экономное решение.

Радиус внутренней окружности и площадь

Для того чтобы вычислить площадь треугольника, вписанного в окружность, используют лишь радиус и длины сторон многоугольника:

Если в условии задачи напрямую не дано значение радиуса, а только площадь, то указанная формула площади трансформируется в следующую:

Рассмотрим действие последней формулы на более конкретном примере. Предположим, что дан треугольник, в который вписана окр-ть. Площадь окр-ти составляет 4π, а стороны равны соответственно 4, 5 и 6 см. Вычислим площадь заданного многоугольника при помощи вычисления полупериметра.

Используя вышеуказанный алгоритм, вычислим площадь треугольника через радиус вписанной окружности:

В силу того, что в любой треугольник можно вписать окружность, число вариаций нахождения площади значительно увеличивается. Т.е. поиск площади треугольника, включает в себя обязательное знание длины каждой стороны, а также значение радиуса.

Треугольник, вписанный в окружность геометрия 7 класс

Прямоугольные треугольники, вписанные в окружность

Вывод

Из указанных формул можно убедиться, что сложность любой задачи с использованием вписанной и описанной окружностей заключается только в дополнительных действия по поиску требуемых значений. Задачи подобного типа требуют только досконально понимания сути формул, а также рациональности их применения. Из практики решения отметим, что в будущем центр описанной окружности будет фигурировать и в дальнейших темах геометрии, поэтому запускать ее не следует. В противном случае решение может затянуться с использованием лишних ходов и логических выводов.

Источник