Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона

Формула Герона для нахождения площади треугольника:
– полупериметр треугольника; a,b,c – стороны треугольника.
Через основание и высоту

Формула нахождения площади треугольника с помощью половины его основания и высоту:
a – основание треугольника; h – высота треугольника.
Через две стороны и угол

Формула нахождения площади треугольника через две стороны и угол между ними:
a,b – стороны треугольника; α – угол между сторонами.
Через сторону и два прилежащих угла

Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
<
a– сторона треугольника; α и β – прилежащие углы.
Площадь прямоугольного треугольника

Прямоугольный треугольник – треугольник у которого один из углов прямой, т.е. равен 90°.
Формула нахождения площади прямоугольного треугольника через катеты:
a, b – катеты треугольника.
Площадь равнобедренного треугольника через стороны

Равнобедренный треугольник – треугольник, в котором две стороны равны. А значит, равны и два угла.
Формула нахождения площади равнобедренного треугольника через две стороны:
a, b – стороны треугольника.
Площадь равнобедренного треугольника через основание и угол

Формула нахождения площади равнобедренного треугольника через основание и угол:
a – основание равнобедренного треугольника; α – угол между сторонами.
Площадь равностороннего треугольника через стороны

Равносторонний треугольник – треугольник, в котором все стороны равны, а каждый угол равен 60°.
Формула нахождения площади равностороннего треугольника через сторону:
a – сторона равностороннего треугольника.
Площадь равностороннего треугольника через высоту

Формула нахождения площади равностороннего треугольника через высоту:
h – высота равностороннего треугольника.
Площадь равностороннего треугольника через радиус вписанной окружности

Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
r – радиус вписанной окружности равностороннего треугольника.
Площадь равностороннего треугольника через радиус описанной окружности

Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
r – радиус описанной окружности равностороннего треугольника.
Площадь треугольника через радиус описанной окружности и три стороны

Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
a, b, c – стороны треугольника; r – радиус описанной окружности треугольника.
Площадь треугольника через радиус вписанной окружности и три стороны

Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
p – полупериметр треугольника;a, b, c – стороны треугольника; r – радиус вписанной окружности треугольника.

{S = dfrac{1}{2} cdot a cdot h}
Задача нахождения площади треугольника довольно распространена не только в науке, но и в быту. Для вас мы разработали калькулятор для нахождения площади любого треугольника – равнобедренного, равностороннего, прямоугольного или обыкновенного (разностороннего) по 22 формулам.
- Калькулятор площади треугольника
- Площадь треугольника
- через основание и высоту
- через две стороны и угол между ними
- через сторону и два прилежащих угла
- через радиус описанной окружности и 3 стороны
- через радиус вписанной окружности и 3 стороны
- по формуле Герона
- Площадь прямоугольного треугольника
- через катеты
- через гипотенузу и прилежащий угол
- через катет и прилежащий угол
- через радиус вписанной окружности и гипотенузу
- через вписанную окружность
- по формуле Герона
- через катет и гипотенузу
- Площадь равнобедренного треугольника
- через основание и сторону
- через основание, боковую сторону и угол
- через основание и высоту
- через боковые стороны и угол между ними
- через основание и угол между боковыми сторонами
- Площадь равностороннего треугольника
- через сторону
- через высоту
- через радиус описанной окружности
- через радиус вписанной окружности
- Примеры задач
Площадь треугольника
Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.
Площадь треугольника через основание и высоту
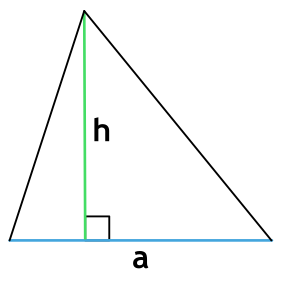
{S = dfrac{1}{2} cdot a cdot h}
a – длина основания
h – высота, проведенная к основанию
Площадь треугольника через две стороны и угол между ними
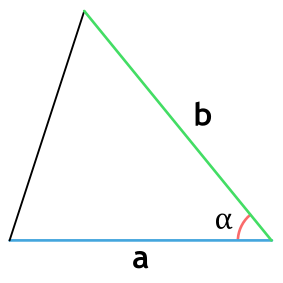
{S = dfrac{1}{2} cdot a cdot b cdot sin(alpha)}
a и b – стороны треугольника
α – угол между сторонами a и b
Площадь треугольника через сторону и два прилежащих угла
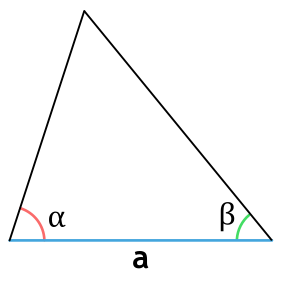
{S = dfrac{a^2}{2} cdot dfrac{sin{(alpha)} cdot sin{(beta)}}{sin{(gamma)}}}
{gamma = 180 – (alpha + beta)}
a – сторона треугольника
α и β – прилежащие к стороне a углы
Площадь треугольника через радиус описанной окружности и 3 стороны
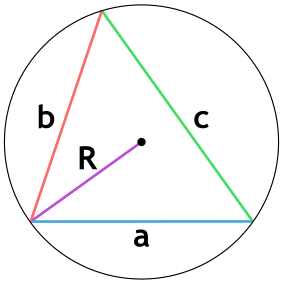
{S = dfrac{a cdot b cdot c}{4 cdot R}}
a, b и c – стороны треугольника
R – радиус описанной окружности
Площадь треугольника через радиус вписанной окружности и 3 стороны
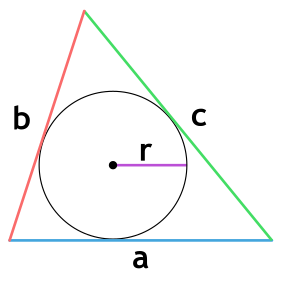
{S = r cdot dfrac{a + b + c}{2}}
a, b и c – стороны треугольника
r – радиус вписанной окружности
Площадь треугольника по формуле Герона
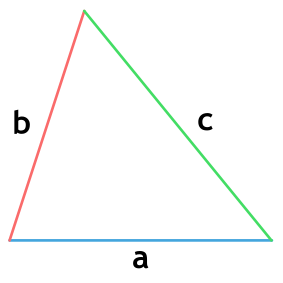
{S = sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)}}
{p= dfrac{a+b+c}{2}}
a, b и c – стороны треугольника
p – полупериметр треугольника
Площадь прямоугольного треугольника
Прямоугольный треугольник — это треугольник, в котором один угол прямой (равен 90 градусов).
Площадь прямоугольного треугольника через катеты

{S = dfrac{1}{2} cdot a cdot b}
a и b – стороны треугольника
Площадь прямоугольного треугольника через гипотенузу и прилежащий угол
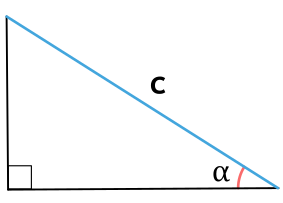
{S = dfrac{1}{4} cdot c^2 cdot sin{(2 alpha)}}
c – гипотенуза прямоугольного треугольника
α – прилежащий к гипотенузе c угол
Площадь прямоугольного треугольника через катет и прилежащий угол
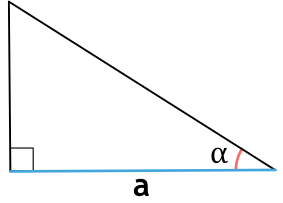
{S = dfrac{1}{2} cdot a^2 cdot tg{(alpha)}}
a – катет прямоугольного треугольника
α – прилежащий к катету a угол
Площадь прямоугольного треугольника через радиус вписанной окружности и гипотенузу
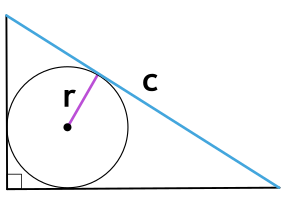
{S = r cdot (r+c)}
r – радиус вписанной окружности
c – гипотенуза прямоугольного треугольника
Площадь прямоугольного треугольника через вписанную окружность

{S = c_1 cdot c_2}
с1 и с2 – отрезки, полученные делением гипотенузы точкой касания окружности
Площадь прямоугольного треугольника по формуле Герона
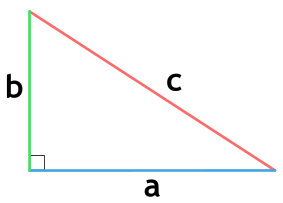
{S = (p-a) cdot (p-b)}
{p= dfrac{a+b+c}{2}}
a, b и c – стороны треугольника
p – полупериметр треугольника
Площадь прямоугольного треугольника через катет и гипотенузу
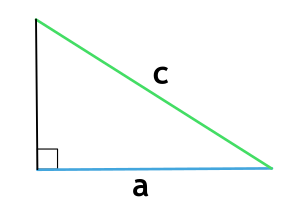
{S = dfrac{1}{2} cdot a cdot sqrt{c^2 – a^2}}
a – катет прямоугольного треугольника
c – гипотенуза прямоугольного треугольника
Площадь равнобедренного треугольника
Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по длине.
Площадь равнобедренного треугольника через основание и сторону
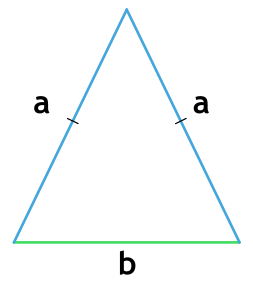
{S = dfrac{b}{4} sqrt{4a^2 – b^2}}
a – боковая сторона равнобедренного треугольника
b – основание равнобедренного треугольника
Площадь равнобедренного треугольника через основание, сторону и угол
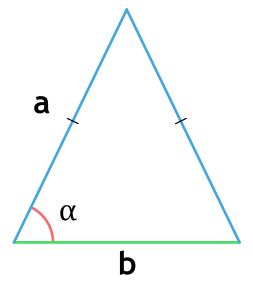
{S = dfrac{1}{2} cdot a cdot b cdot sin{(alpha)}}
a – боковая сторона равнобедренного треугольника
b – основание равнобедренного треугольника
α – угол между основанием и боковой стороной
Площадь равнобедренного треугольника через основание и высоту
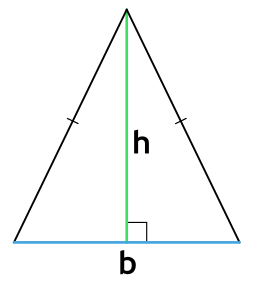
{S = dfrac{1}{2} cdot b cdot h}
b – основание равнобедренного треугольника
h – высота, проведенная к основанию равнобедренного треугольника
Площадь равнобедренного треугольника через боковые стороны и угол между ними
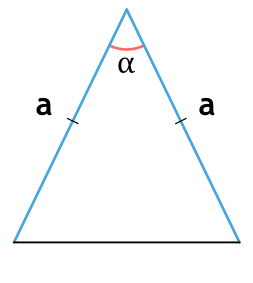
{S = dfrac{1}{2} cdot a^2 cdot sin(alpha)}
a – боковые стороны равнобедренного треугольника
α – угол между боковыми сторонами
Площадь равнобедренного треугольника через основание и угол между боковыми сторонами

{S = dfrac{b^2}{4 cdot tg {( dfrac{alpha}{2} )}}}
b – основание равнобедренного треугольника
α – угол между боковыми сторонами
Площадь равностороннего треугольника
Равносторонний треугольник – треугольник, у которого все стороны равны.
Площадь равностороннего треугольника через сторону

{S = dfrac{sqrt{3} cdot a^2}{4}}
a – сторона равностороннего треугольника
Площадь равностороннего треугольника через высоту
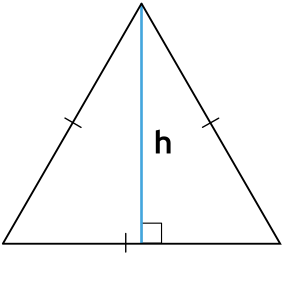
{S = dfrac{h^2}{sqrt{3}}}
h – высота равностороннего треугольника
Площадь равностороннего треугольника через радиус описанной окружности

{S = dfrac{3 sqrt{3} cdot R^2}{4}}
R – радиус описанной окружности
Площадь равностороннего треугольника через радиус вписанной окружности

{S = 3 sqrt{3} cdot r^2}
r – радиус описанной окружности
Примеры задач на нахождение площади треугольника
Задача 1
Найдите площадь треугольника со сторонами 13 14 15.
Решение
Для решения задачи воспользуемся формулой Герона.
S = sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)}
Для начала нам необходимо найти полупериметр p:
p= dfrac{a+b+c}{2}p= dfrac{13+14+15}{2}= dfrac{42}{2} = 21
Теперь можем подставить его в формулу Герона и найти ответ:
S = sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)} = sqrt{21 cdot (21-13) cdot (21-14) cdot (21-15)} = sqrt{21 cdot (8) cdot (7) cdot (6)} = sqrt{21 cdot 336} = sqrt{7056} = 84 : см^2
Ответ: 84 см²
Убедимся в правильности решения с помощью калькулятора .
Задача 2
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 100.
Решение
Воспользуемся формулой.
S = dfrac{1}{2} cdot a cdot sqrt{c^2 – a^2} = dfrac{1}{2} cdot 28 cdot sqrt{100^2 – 28^2} = dfrac{1}{2} cdot 28 cdot sqrt{10000 – 784} = dfrac{1}{2} cdot 28 cdot sqrt{9216} = dfrac{1}{2} cdot 28 cdot 96 = 14 cdot 96 = 1344 : см^2
Ответ: 1344 см²
Проверим ответ на калькуляторе .
Задача 3
Найдите площадь прямоугольного треугольника если его катет и гипотенуза равны соответственно 15 и 17.
Решение
Задача аналогична предыдущей, поэтому решение очень похоже.
S = dfrac{1}{2} cdot a cdot sqrt{c^2 – a^2} = dfrac{1}{2} cdot 15 cdot sqrt{17^2 – 15^2} = dfrac{1}{2} cdot 15 cdot sqrt{289 – 225} = dfrac{1}{2} cdot 15 cdot sqrt{64} = dfrac{1}{2} cdot 15 cdot 8 = 15 cdot 4 = 60 : см^2
Ответ: 60 см²
Проверка .
Задача 4
Найдите площадь прямоугольного треугольника, если гипотенуза его равна 40 см а острый угол равен 60°.
Решение
Для решения задачи воспользуемся формулой.
S = dfrac{1}{4} cdot c^2 cdot sin{(2 alpha)} = dfrac{1}{4} cdot 40^2 cdot sin{(2 cdot 60°)} = dfrac{1}{4} cdot 1600 cdot sin{(120°)} = 400 cdot dfrac{sqrt{3}}{2} = 200 sqrt{3} : см^2 approx 346.41016 : см^2
Ответ: 200 sqrt{3} : см^2 approx 346.41016 : см^2
Проверка .
Задача 5
Найдите площадь равнобедренного треугольника, если боковая сторона равна 7 см а основание 4 см.
Решение
В этой задаче используем формулу для нахождения площади равнобедренного треугольника через основание и боковую сторону.
S = dfrac{b}{4} sqrt{4a^2 – b^2} = dfrac{4}{4} sqrt{4 cdot 7^2 – 4^2} = sqrt{4 cdot 49 – 16} = sqrt{196 – 16} = sqrt{180} = sqrt{36 cdot 5} = 6sqrt{5} : см^2 approx 13.41641 : см^2
Ответ: 6sqrt{5} : см^2 approx 13.41641
Проверка .
Задача 6
Найдите площадь равнобедренного треугольника, если его основание равно 30, боковая сторона равна 17.
Решение
Решим эту задачу по анологии с предыдущей.
S = dfrac{b}{4} sqrt{4a^2 – b^2} = dfrac{30}{4} sqrt{4 cdot 17^2 – 30^2} = dfrac{30}{4} sqrt{4 cdot 289 – 900} = dfrac{30}{4} sqrt{1156 – 900} = dfrac{30}{4} sqrt{256} = dfrac{30}{4} cdot 16= 30 cdot 4 = 120 : см^2
Ответ: 120 см²
Проверка .
Задача 7
Найдите площадь равностороннего треугольника со стороной 12 см.
Решение
Используем для решения задачи формулу.
S = dfrac{sqrt{3} cdot a^2}{4} = dfrac{sqrt{3} cdot 12^2}{4} = dfrac{sqrt{3} cdot 144}{4} = 36 sqrt{3} : см^2 approx 62.35383 : см^2
Ответ: 36 sqrt{3} : см^2 approx 62.35383 : см^2
Проверка .
Как найти площадь любого треугольника
Вспоминаем геометрию: формулы для произвольных, прямоугольных, равнобедренных и равносторонних фигур.

Как найти площадь любого треугольника
Посчитать площадь треугольника можно разными способами. Выбирайте формулу в зависимости от известных вам величин.
Зная сторону и высоту
- Умножьте сторону треугольника на высоту, проведённую к этой стороне.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a — сторона треугольника.
- h — высота треугольника. Это перпендикуляр, опущенный на сторону или её продолжение из противоположной вершины.
Зная две стороны и угол между ними
- Посчитайте произведение двух известных сторон треугольника.
- Найдите синус угла между выбранными сторонами.
- Перемножьте полученные числа.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a и b — стороны треугольника.
- α — угол между сторонами a и b.
Зная три стороны (формула Герона)
- Посчитайте разности полупериметра треугольника и каждой из его сторон.
- Найдите произведение полученных чисел.
- Умножьте результат на полупериметр.
- Найдите корень из полученного числа.
- S — искомая площадь треугольника.
- a, b, c — стороны треугольника.
- p — полупериметр (равен половине от суммы всех сторон треугольника).
Зная три стороны и радиус описанной окружности
- Найдите произведение всех сторон треугольника.
- Поделите результат на четыре радиуса окружности, описанной вокруг прямоугольника.
- S — искомая площадь треугольника.
- R — радиус описанной окружности.
- a, b, c — стороны треугольника.
Зная радиус вписанной окружности и полупериметр
Умножьте радиус окружности, вписанной в треугольник, на полупериметр.
- S — искомая площадь треугольника.
- r — радиус вписанной окружности.
- p — полупериметр треугольника (равен половине от суммы всех сторон).
Как найти площадь прямоугольного треугольника
- Посчитайте произведение катетов треугольника.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a, b — катеты треугольника, то есть стороны, которые пересекаются под прямым углом.
Как найти площадь равнобедренного треугольника
- Умножьте основание на высоту треугольника.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a — основание треугольника. Это та сторона, которая не равняется двум другим. Напомним, в равнобедренном треугольнике две из трёх сторон имеют одинаковую длину.
- h — высота треугольника. Это перпендикуляр, опущенный на основание из противоположной вершины.
Как найти площадь равностороннего треугольника
- Умножьте квадрат стороны треугольника на корень из трёх.
- Поделите результат на четыре.
- S — искомая площадь треугольника.
- a — сторона треугольника. Напомним, в равностороннем треугольнике все стороны имеют одинаковую длину.
Читайте также 🧠👨🏻🎓✍🏻
- 7 причин полюбить математику
- ТЕСТ: Помните ли вы геометрию?
- 10 хитрых головоломок со спичками для тренировки воображения
- Интересные математические факты для тех, кто хочет больше узнать о мире вокруг
- ТЕСТ: Сможете ли вы решить простые математические примеры?
Содержание:
- Формулы
- Примеры вычисления площади треугольника
Формулы
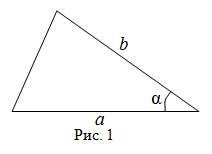
Первый способ. Чтобы найти площадь треугольника, надо найти полупроизведение двух его сторон на синус угла между ними (рис. 1).
То есть если известны длины двух сторон треугольника
$ABC$, которые равны
$a$ и
$b$, а также угол
$alpha$ между этими сторонами, то искомая площадь:
$$mathrm{S}_{Delta A B C}=frac{1}{2} a b sin alpha$$
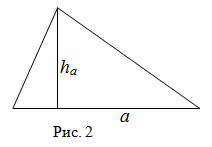
Второй способ. Чтобы найти площадь треугольника, нужно сторону умножить на высоту, проведенную к этой стороне (рис. 2),
и полученное произведение поделить на два. То есть если сторона треугольника
$ABC$ равна
$a$, а длина высоты, проведенной к этой стороне
– $h_{a}$, то имеет место формула:
$$mathrm{S}_{Delta A B C}=frac{1}{2} a h_{a}$$
Третий способ. Чтобы найти площадь треугольника
$ABC$, если известны длины всех его трех сторон
$a$,
$b$ и
$c$, нужно воспользоваться формулой Герона:
$$mathrm{S}_{Delta A B C}=sqrt{p(p-a)(p-b)(p-c)}$$
где $p=frac{a+b+c}{2}$ – полупериметр.
Четвертый способ. Чтобы найти площадь треугольника
$ABC$, нужно радиус
$r$ вписанной в этот треугольник окружности умножить на полупериметр
$p$ треугольника:
$$mathrm{S}_{Delta A B C}=r p$$
Пятый способ. Чтобы найти площадь треугольника со сторонами
$a$,
$b$ и
$c$, нужно произведение этих сторон поделить на четыре радиуса
$R$, описанной около треугольника окружности:
$$mathrm{S}_{Delta A B C}=frac{a b c}{4 R}$$
Примеры вычисления площади треугольника
Пример
Задание. Найти площадь треугольника
$ABC$, если известны длины двух его сторон 3 см и 5 см
соответственно, а также угол между этими сторонами, который равен
$30^{circ}$.
Решение. Искомая площадь равна полупроизведению сторон на синус угла между ними, то есть
$begin{aligned} mathrm{S}_{Delta A B C}=& frac{1}{2} a b sin alpha=frac{1}{2} cdot 3 cdot 5 cdot sin 30^{circ}=\ &=frac{15}{2} cdot frac{1}{2}=frac{15}{4}left(mathrm{cm}^{2}right) end{aligned}$
Ответ. $mathrm{S}_{Delta A B C}=frac{15}{4}$ (см2)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Чему равна высота треугольника
$ABC$, проведенная к стороне длины 2 см, если площадь
этого треугольника равна 6 см2 ?
Решение. Так как площадь треугольника в два раза меньше произведения стороны на высоту, проведенную к этой стороне:
$$mathrm{S}_{Delta A B C}=frac{1}{2} a h_{a}$$
то отсюда получаем, что искомая высота
$h_{a}=frac{2 mathrm{S}_{Delta A B C}}{a}=frac{2 cdot 6}{2}=6$ (см)
Ответ. $h_{a}=6$ (см)
Читать дальше: как найти площадь прямоугольного треугольника.
Остались вопросы?
Здесь вы найдете ответы.
Как найти площадь треугольника с прямыми углами при условии, что длина его
катета составляет 5 сантиметров, а гипотенузы – 13 сантиметров?
Длина катета (а) = 5 см.
Длина гипотенузы (с) = 13 см.
Используя теорему Пифагора, определим длину второго катета:
в² = с² -а² = 169 – 25 = 144
в = 12
Рассчитать площадь прямоугольного треугольника можно по формуле:
S = 0,5ав = 0,5*5*12 = 30
Ответ: S прямоугольного треугольника равна 30 кв.см.
Как найти площадь треугольника?
Для того чтобы вычислить площадь (S) треугольника, следует произвести
умножение длины его основания (а) на длину высоты к основанию (h), а затем
разделить полученное число пополам:
S=1/2 (а*h)
Как найти площадь треугольника при условии, что длина каждой его стороны
является известной величиной?
Если длина каждой стороны треугольника известна, то вычислить его площадь
(S) можно, используя формулу Герона:
S= √ (p * (p – a)*(p – b)*(p – c))
a,b,c – длина каждой из трех сторон;
р – полупериметр треугольника, который равен сумме длин всех сторон,
разделенной на 2.
Как найти площадь треугольника, зная 3 точки: А(1;8), В(7;8) и С(6;6)?
По условию задачи известны 3 точки, являющиеся вершинами треугольника АВС,
площадь (S) которого нужно вычислить. Это точки А(1;8), В(7;8) и С(6;6).
Две из трех известных точек расположены на прямой, которая параллельна оси
Х, ввиду того что координаты Ya и Yb одинаковы. Это точки А и В. Это
означает, что высота треугольника (h), которая опущена на сторону АВ из
вершины С (6;6), является числом, полученным в результате вычитания из
координаты Ya или Yb координаты Yc:
8-6=2.
Для того чтобы определить длину стороны АВ, нужно от координаты Xb вычесть
координату Xa:
7-1=6.
Теперь можно вычислить площадь треугольника (S):
(1/2)*AB*h = (1/2)*6*2 =6 ед.
Ответ: S = 6 ед.кв.
Как найти площадь треугольника через синус при условии, что известны две
стороны а = 3 и b = 4, а также угол γ= 30°?
Формула расчета площади треугольника (S) через синус применима в случае,
когда известны длины 2-х его сторон и угол, образованный между ними. При
этом следует воспользоваться таблицей синусов, согласно которой синус угла
в 30° = 0,5.
S = (1/2)*3*4*0,5=3.
Ответ: S треугольника = 3 см.кв.
Как найти площадь треугольника через синус, если известно, что длина одной
его стороны равна 12, другой – 16, а синус угла между ними – ¼?
Зная длины двух сторон треугольника и синус угла между ними, можно
рассчитать его площадь. Она будет равна ½ произведений длин его сторон,
умноженной на значение синуса угла между ними:
12*16*0,5*0,25=24.
Ответ: S треугольника = 24 см.кв.
Как найти площадь треугольника АВС, а также вычислить синус его угла А,
зная, что AC=BC=5;AB=6?
Площадь треугольника АВС можно рассчитать, воспользовавшись формулой
Герона:
S=√(p(p-a)(p-b)(p-c)=√(8*2*3*3)=√144=12 (ед.²).
Найти синус угла А можно по следующей формуле:
S=12 * АВ * АС * sin∠A
12 * 6 * 5 * sin∠A = 1215 * sin∠A = 12
sin∠A = 1215 = 0,8
Ответ: sin∠A = 0,8.
Как найти площадь треугольника через синус, если длина одной стороны равна 5
см, другой – 12 см, а синус угла, образованного между ними равен 0,2?
Для того чтобы вычислить площадь треугольника (S), зная параметры,
указанные в задаче, следует воспользоваться нижеприведенной формулой:
S= (a b sinα)/2 = (5·12·0,2)/2 =6
Ответ: S треугольника = 6 см.кв.
Как найти синус угла С в треугольнике АВС, если известно, что АВ=ВС=1 и
АС=2?
Для начала нужно убедиться в том, что заданная фигура с параметрами
АВ=ВС=1, АС=2 действительно представляет собой треугольник.
Длины двух сторон треугольника в сумме не могут быть равны или меньше
длине его третьей стороны. В данном случае:
1+1=2, то есть АВ+ВС=АС
Следует помнить, что говорить о фигуре как о треугольнике можно только в
том случае, когда сумма длин двух любых его сторон больше длины третьей
стороны.
Ответ: при заданных параметрах треугольника нет, и вычислить синус угла в
данном случае невозможно.
Как найти синус наибольшего внутреннего угла треугольника АВС, если
известно, что AB=13, BC=14, AC=15?
Сторона треугольника, которая имеет наибольшую длину, является
противоположной его наибольшему углу. В данном случае сторона АС имеет
наибольшую длину (15 см), это значит, что наибольшим углом является угол
В.
Перейдем к построению треугольника.
Нужно провести к стороне ВС высоту АН. Синусом наибольшего угла В является
отношение АН:АВ. Теперь можно вычислить высоту из площади треугольника,
рассчитанной по формуле Герона и равной 84 см:
S=ah:2
h=2S:a
h=ВН=2*84:14= 12
sin B=12:13=0,923
Ответ: sin B = 0,923.
Чему равна площадь треугольника, если две сходственные стороны подобного ему
треугольника, площадь которого 32 см.кв., равны 5 см и 10 см?
В условии говорится о том, что треугольники являются подобными. Также
приведены длины двух сходственных сторон. Эти данные можно использовать,
для того чтобы вычислить коэффициент подобия:
К = 10/5 = 2
Известно, что квадрат коэффициента подобия равен отношению площадей двух
треугольников, являющихся подобными. Это означает, что в заданном случае
площадь второго треугольника в четыре раза превышает площадь первого из
них. Зная это, можно найти площадь первого треугольника следующим образом:
32:4 = 8 см.кв.
Ответ: Площадь первого треугольника – 8 см.кв.
Чему равна площадь треугольника АВС, если он является прямоугольным, и
известно, что катеты равны 2,5 см и 4 см?
Произведение катетов прямоугольного треугольника, разделенное на два,
равно его площади. Для того чтобы дать ответ на поставленный вопрос, нужно
перемножить катеты (2,5*4=10) и разделить полученное число на 2 (10/2=5).
Ответ: Площадь прямоугольного треугольника равна 5 см.кв.
Чему равна площадь треугольника, образовавшегося в результате разделения на
два треугольника квадрата, сторона которого равна 4 см?
Для начала нужно рассчитать площадь квадрата:
4*4 = 16 см.кв.
Теперь можно вычислить площадь одного из получившихся в результате
треугольников:
16/2 = 8 см.кв.
Ответ: Площадь треугольника равна 8 см.кв.
Дано: два подобных треугольника, длины двух сходственных сторон которых
равны 3 см и 9 см Площадь одного из треугольников – 9 см.кв. Чему равна
площадь другого треугольника?
Квадраты сходственных сторон двух подобных треугольников относятся как их
площади. Это значит, что:
(9/3)²=х/9,
где х – это площадь треугольника, которую нужно вычислить.
9=х/9,
откуда х=81см.кв.
Ответ: Площадь треугольника – 81 см.кв.
Известна площадь треугольника (208 см), основание которого было разбито
высотой на два отрезка длиной 22 см и 10 см. Чему равна площадь
треугольника, являющегося меньшим из двух образовавшихся?
Сначала нужно найти длину всего основания:
10+22 = 32 см.
Теперь можно вычислить площадь меньшего из двух треугольников:
208 / 32 * 10 = 65 см.кв.
Ответ: Площадь меньшего треугольника составляет 65 см.кв.
Чему равна площадь треугольника через синус, если две его стороны имеют
длины 3 см и 8 см, а угол между ними равен 120?
Для того чтобы рассчитать площадь треугольника, нужно найти
полупроизведение двух его сторон на синус угла, образованного между ними:
S=1/2 * 3*8*sin120=1/2*3*8*cos30=12*√3/2=6√3.
Какова формула расчета площади треугольника?
Площадь треугольника можно найти, если разделить на два число, полученное
в результате умножения высоты (h), опущенной на его основание, на длину
самого основания (а):
S=1/2*(h*a).
Как вычислить площадь треугольника по формуле 3-го класса?
В случае треугольника с прямыми углами, его площадь вычисляется по
формуле:
S=a*b/2,
где а и b – это стороны, которые прилегают к прямому углу.
Во всех остальных случаях рассчитать площадь треугольника можно следующим
образом:
S=a*h/2,
где а – сторона,
h – высота.
Какую формулу нужно использовать, чтобы вычислить площадь треугольника, зная
2 его стороны и угол, образованный между ними?
Для вычисления площади треугольника по длинам двух его сторон и
находящемуся между ними углу, нужно пользоваться формулой:
S = 1a*b*sin γ2.
Возможно ли доказать, что по формуле S= 1/2 Pr можно вычислить площадь
треугольника?
Имеется:
– треугольник АВС;
– О – центр вписанной окружности, точка пересечения биссектрис;
– Н – точка касания окружности на АВ;
– К – точка на ВС;
М – точка на АС.
Нужно провести ОА, ОВ, ОС, а также перпендикулярные радиусы в точки
касания – ОН, ОК, ОМ, ОН=ОК=ОМ=радиус=r. Площадь треугольника АВО будет
равна:
S = 1/2АВ*ОН.
Площадь ВОС рассчитывается так:
S = 1/2ВС*ОК.
Площадь АОС:
S = 1/2АС*ОМ
Площадь заданного треугольника АВС можно найти следующим образом:
S АВС = S АОВ + S ВОС + S АОС = 1/2АВ*ОН+1/2ВС*ОК+1/2АС*ОМ.
Однако ОН=ОК=ОМ=r.
Тогда S АВС = 1/2*r*(АВ+ВС+АС).
Но АВ+ВС+АС= периметр Р, что означает, что
S АВС = 1/2*Р*r.
Как вычислить площадь треугольника при помощи формулы Герона, если дано, что
его стороны равны 6 см, 8 см и 10 см?
Сначала следует произвести расчет полупериметра (р):
р=(6+8+10):2=12 см.
Далее, используя формулу Герона, можно найти площадь треугольника (S):
S=√(p(p-a)(p-b)(p-c)=√(12*6*4*2)=√576=24 см.кв.
Каким образом можно доказать тот факт, что радиус окружности, которая
описана вокруг треугольника, вычисляется по формуле R=a*b*c/4S, где а,b, с –
это стороны треугольника, S – его площадь?
Высота к стороне треугольника находится по формуле b*sin(C). Отсюда можно
найти его площадь S = a*b*sin(C)/2. При этом следует принимать во внимание
теорему синусов, согласно которой c = 2*R*sin(C); или sin(C) = c/(2*R).
Тогда площадь S = a*b*c/4R. Именно это требовалось доказать.
Что представляет собой формула расчета площади треугольника ROF, в случае
если R(0;5),О(0;0),F(2;0)?
Полагаясь на координаты, можно утверждать, что точка R лежит на оси Y и
находится на расстоянии в пять единиц от начала отсчета. При этом точка F
находится на оси X, на расстоянии двух единиц от начала отсчета. Заданный
треугольник является прямоугольным. RO равна 5 единицам длины, FO – двум
единицам длины. В этом случае площадь треугольника ROF равна:
S =RO*FO/2=5*2/2=5(единиц длины)².
Как вычислить площадь треугольника, использовав формулу Герона?
Формула Герона, предназначенная для вычисления площади треугольника,
выгладит так:
S = √(р * (р-а)(p-b)(p-c) ),
где а,b, с – это стороны треугольника,
р – полупериметр, рассчитываемый как Р/2.
Какова формула, по которой можно вычислить площадь треугольника, зная три
стороны и радиус описанной окружности?
Если известны длины трех сторон треугольника (а,b, с), а также радиус
описанной окружности (R), то можно рассчитать площадь треугольника (S) по
следующей формуле:
S = a*b*с/4R.
Как можно найти длину одной стороны треугольника b, используя формулу
расчета его площади S=abc/4R?
В случае необходимости выразить длину одной из сторон треугольника b из
формулы расчета его площади S=abc/4R, нужно произвести умножение всего
выражения на 4R:
S4R=abc.
После этого нужно произвести деление всего на ac:
S4R/ac=b.
Можно ли привести доказательство того, что радиус вписанной в треугольник
окружности (r), рассчитывается по формуле r =2S/a+b+c, в которой а,b, с –
это стороны треугольника, S – его площадь?
В случае соединения вершин треугольника с центром окружности, вписанной в
него, в результате произойдет его деление на 3 треугольника. Радиус в
точке касания будет выступать в роли высоты в каждом из них. Из этого
вытекает формула:
S = pr,
где р – полупериметр.
Возможно ли из формулы S=aha/2, используемой для вычисления площади
треугольника, выразить и вычислить одну из его сторон а, при условии, что
площадь равна 21 см, а высота ha – 7 см?
Ответ на поставленный вопрос выглядит следующим образом:
S=aha/2
a=2S/ha
a=2*21/7=6 см.
Ответ: Длина стороны а равна 6 см.
Какую формулу нахождения площади треугольника следует применять, когда
известно, что три катета равны 3 см, 5 см и 4 см?
Формула S=12 bа для прямоугольного треугольника с двумя катетами (а и b)
и гипотенузой с. В представленной задаче а=3 см, b=4 см, с=5 см. Согласно
таблице Пифагора с²=а²+в². В нашем случае 5²=3²+4², 25=9+16) и S=12*3*4=6
cм. кв.
Какова формула нахождения площади треугольника, длины трех сторон которого
равны 16 см, 24 см и 32 см?
Площадь треугольника можно рассчитать, применяя формулу Герона:
S=√p*(p-a)*(p-b)*(p-c),
в которой р обозначает полупериметр, вычисляемый как сумма длин всех
сторон треугольника, разделенная на 2: р=(16+24+32)/2=36.
В формуле стороны треугольника обозначены как a, b, c.
S=√36*20*12*4 = 48√15 cм.кв.
S = a*b*c/(4R) – это формула нахождения площади треугольника. В ней a, b и
с – это его стороны, а R – это радиус окружности, которая описана вокруг
данного треугольника. Каким образом можно использовать данную формулу,
чтобы найти площадь треугольника, если а = 11, b = 13, с = 20 и R = 65/6?
Сначала нужно перемножить длины всех сторон треугольника:
a*b*с = 11*13*20 = 2860.
Четыре радиуса окружности равны:
4/(65/6) = 130/3.
Из этого следует, что площадь треугольника будет равна:
S = 2860/(130/3) = 8580/130 = 66 см. кв.
Каковы формулы нахождения площади треугольника?
Существует несколько формул, которыми можно пользоваться для вычисления
площади треугольника:
1. S = 1/2*bh, в которой b – это основание фигуры, а h – проведенная к
нему высота.
2. S = 1/2*ahₐ, где а обозначает длину стороны треугольника, а hₐ –
проведенная к этой стороне высота.
3. Формула Герона: S = √(р * (р-а)(p-b)(p-c) ), в которой стороны
треугольника обозначены как а,b, с. Полупериметр (Р/2) обозначен как р.
4. S=р*r, или полупериметр*радиус вписанной окружности.
5. S= 1/2*ab*sinα, где a и b – это стороны треугольника, α – угол,
образованный между ними.
6. S = (a*b*c) / 4R, в которой радиус описанной окружности обозначен R, а
стороны треугольника – а,b,с.
Прямоугольник, периметр которого равен 40 см, вписан в треугольник со
сторонами 20 см, 34 см и 42 см таким образом, что одна из его сторон лежит
на стороне треугольника, являющейся наибольшей. Чему равны стороны
треугольника?
Площадь треугольника можно вычислить по формуле Герона:
S = √(р * (р-а)(p-b)(p-c)) = √ (48*(48-20)*(48-34)*(48-42)) = 336 см. кв.
Отсюда следует, что высота, проведенная к стороне 42 рассчитывается так:
Н = 2*336/48 = 16.
Верхняя сторона прямоугольника отсекает подобный треугольник (x – сторона
II основанию 42, y – сторона II высоте H = 16), из чего следует очевидная
пропорция (16 – y)/16 = x/42, согласно которой отношение высот равно
отношению оснований. По условию x + y = 20. Решив данную систему двумя
уравнениями с двумя неизвестными, получаем следующее:
х = 84/13; y = 176/13.
Длина большей стороны треугольника равна 16 см. Число 0,4 является
разностью длин двух других его сторон. Чему равны стороны треугольника при
условии, что его периметр равен 0,38 м?
Схема решения задачи:
а (большая сторона треугольника) = 16 см.
b-с = 0,4 см., b = 0,4+с.
Периметр (Р) = 38 см.
16+0,4+с+с = 38 см.
2с = 21,6 см.
с = 21,6/2 = 10,8 см.
b = 10,8+0,4 = 11,2 см.
Каким способом можно доказать то, что два треугольника с равными сторонами
равны между собой при условии, что стороны одного из них равны стороне
другого?
Для равносторонних треугольников характерно равенство длин всех трех
сторон. Если одна его сторона равна а, то и обе другие тоже будут равны а.
Если же все стороны треугольников равны, то это равенство соблюдается по 3
признаку.
Длины двух сторон треугольника с периметром 19 см равны 6 см и 4 см. Чему
равна третья сторона данного треугольника?
Известно, что периметр треугольника является суммой длин всех его сторон и
рассчитывается по формуле:
Р = а+ b+с.
В данном случае:
19 = 6+4+с
19 = 10+с
с = 19-10 = 9 см.
Ответ: Длина третьей стороны треугольника – 9 см.
Наименьшая сторона треугольника имеет длину 5 см. Чему равны другие стороны
этого треугольника при условии, что стороны треугольника, являющегося
подобным ему, равны 8 см, 2 см и 9 см?
Сначала необходимо вычислить коэффициент подобия двух этих треугольников.
Он равен отношению сходственных сторон:
к = 5/2.
Теперь нужно рассчитать длины других сторон первого из треугольников. Одна
из них, которая является сходственной стороне второго из треугольников
длиной 8 см, рассчитывается следующим образом:
8*к = 9*5/2 = 20 см.
Еще одна сторона первого треугольника, сходственная стороне другого из
них, которая имеет длину 9 см, вычисляется так:
9*к = 9*5/2 = 22,5 см.
Три стороны треугольника имеют длины 8 см, 24 см и 22 см. Произведение длин
всех трех сторон подобного треугольника равно 66. Чему равны стороны
подобного треугольника?
Следует найти отношение этих сторон:
4/12/11.
Отношение всех сторон подобного треугольника будет таким же.
Одну из сторон подобного треугольника обозначим 4х, вторую сторону – 12х,
а третью – 11х. В результате получается следующее уравнение:
4х*12х*11х = 66
528х^3 = 66
x^3 = 66:528
x^3 = 0,125
x = корень 3-ей степени из 0,125 = 0,5.
Первая сторона треугольника = 4х = 4*0,5 = 2 см.
Вторая сторона треугольника = 12х = 12*0,5 = 6 см.
Третья сторона треугольника = 11х = 11*0,5 = 5,5 см.
Проверка: 2*6*5,5 = 66 см.
Две стороны треугольника имеют длины 6 см и 8 см. Его медиана, которая
проведена к третьей из сторон, равна √46 см. Чему равна третья сторона
треугольника?
Имеется треугольник АВС, в котором АВ = 6 см, ВС = 8 см, ВD – медиана на
АС = √46 см (2*АВ в квадрате+2*ВС в квадрате-АС в квадрате). √46 см. =
½*√(2*36+2*64-АС в квадрате), каждую часть возводим в квадрат,
4*46=72+128-АС в квадрате, АС в квадрате=16, АС=4.
Ответ: Длина третьей стороны треугольника равна 4 см.
Две из трех сторон треугольника равны 1 см и 3 см. Чему равна третья сторона
этого же треугольника?
Если предположить, что третья сторона треугольника равна 1 см, то в этом
случае не получится соблюсти неравенство 1 см+1 см = 2 см. В этом случае 3
см больше 2 см, а должно быть меньше. Если длина неизвестной стороны равна
2 см, то неравенство снова не соблюдается: 2 см+1 см = 3, тогда 3 см =3
см, чего тоже не может быть ввиду того, что одна из сторон треугольника
обязательно должна быть меньше суммы двух других его сторон. Если принять
длину третьей стороны равной 3 см, то получается 1 см+3 см = 4 см, 3<4. В этом случае неравенство выполняется. 3 см +3 см=6 см, 3<6. Неравенство снова соблюдено. Возьмем за длину третьей стороны 4 см: 3 см+1 см=4 см, 4=4. Неравенство не соблюдено. Это значит, что и последующими числами оно не будет соблюдено.
Ответ: Третья сторона треугольника равна 3 см.
Как узнать площадь треугольника, являющегося прямоугольным?
Для того чтобы рассчитать площадь треугольника (S) с прямыми углами,
следует воспользоваться приведенной ниже формулой:
S = ½* ab,
где a и b – катеты.
Как узнать площадь треугольника с прямыми углами, катеты которого равны 5 см
и 4 см?
Площадь треугольника с прямыми углами равна ½ от произведения его катетов:
S = (5*4)/2=20/2=10 см. кв.
Как узнать площадь треугольника, используя измерения и вычисления?
Для того чтобы получить возможность вычислить площадь треугольника,
необходимо произвести замеры его основания (а) и высоты (h). Тогда площадь
может быть рассчитана по следующей формуле:
S=ah/2.
Треугольник — это геометрическая фигура, которая образуется в результате пересечения трех отрезков, концы которых не лежат на одной прямой. У любого треугольника есть три стороны, три вершины и три угла.
Онлайн-калькулятор площади треугольника
Треугольники бывают различных видов. Например, существует равносторонний треугольник (тот, у которого все стороны равны), равнобедренный (в нем равны две стороны) и прямоугольный (в котором один из углов прямой, т. е. равен 90 градусам).
Площадь треугольника можно найти различными способами в зависимости от того, какие элементы фигуры известны по условию задачи, будь то углы, длины, либо же вообще радиусы окружностей, связанных с треугольником. Рассмотрим каждый способ отдельно с примерами.
Формула площади треугольника по основанию и высоте
S=12⋅a⋅hS= frac{1}{2}cdot acdot h,
aa — основание треугольника;
hh — высота треугольника, проведенная к данному основанию a.
Найти площадь треугольника, если известна длина его основания, равная 10 (см.) и высота, проведенная к этому основанию, равная 5 (см.).
Решение
a=10a=10
h=5h=5
Подставляем в формулу для площади и получаем:
S=12⋅10⋅5=25S=frac{1}{2}cdot10cdot 5=25 (см. кв.)
Ответ: 25 (см. кв.)
Формула площади треугольника по длинам всех сторон
S=p⋅(p−a)⋅(p−b)⋅(p−c)S= sqrt{pcdot(p-a)cdot (p-b)cdot (p-c)},
a,b,ca, b, c — длины сторон треугольника;
pp — половина суммы всех сторон треугольника (то есть, половина периметра треугольника):
p=12(a+b+c)p=frac{1}{2}(a+b+c)
Эта формула называется формулой Герона.
Найти площадь треугольника, если известны длины трех его сторон, равные 3 (см.), 4 (см.), 5 (см.).
Решение
a=3a=3
b=4b=4
c=5c=5
Найдем половину периметра pp:
p=12(3+4+5)=12⋅12=6p=frac{1}{2}(3+4+5)=frac{1}{2}cdot 12=6
Тогда, по формуле Герона, площадь треугольника:
S=6⋅(6−3)⋅(6−4)⋅(6−5)=36=6S=sqrt{6cdot(6-3)cdot(6-4)cdot(6-5)}=sqrt{36}=6 (см. кв.)
Ответ: 6 (см. кв.)
Формула площади треугольника по одной стороне и двум углам
S=a22⋅sinβsinγsin(β+γ)S=frac{a^2}{2}cdot frac{sin{beta}sin{gamma}}{sin(beta+gamma)},
aa — длина стороны треугольника;
β,γbeta, gamma — углы, прилежащие к стороне aa.
Дано сторону треугольника, равную 10 (см.) и два прилежащих к ней угла по 30 градусов. Найти площадь треугольника.
Решение
a=10a=10
β=30∘beta=30^{circ}
γ=30∘gamma=30^{circ}
По формуле:
S=1022⋅sin30∘sin30∘sin(30∘+30∘)=50⋅123≈14.4S=frac{10^2}{2}cdot frac{sin{30^{circ}}sin{30^{circ}}}{sin(30^{circ}+30^{circ})}=50cdotfrac{1}{2sqrt{3}}approx14.4 (см. кв.)
Ответ: 14.4 (см. кв.)
Формула площади треугольника по трем сторонам и радиусу описанной окружности
S=a⋅b⋅c4RS=frac{acdot bcdot c}{4R},
a,b,ca, b, c — стороны треугольника;
RR — радиус описанной окружности вокруг треугольника.
Числа возьмем из второй нашей задачи и добавим к ним радиус RR окружности. Пусть он будет равен 10 (см.).
Решение
a=3a=3
b=4b=4
c=5c=5
R=10R=10
S=3⋅4⋅54⋅10=6040=1.5S=frac{3cdot 4cdot 5}{4cdot 10}=frac{60}{40}=1.5 (см. кв.)
Ответ: 1.5 (см.кв.)
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
S=p⋅rS=pcdot r,
pp — половина периметра треугольника:
p=a+b+c2p=frac{a+b+c}{2},
a,b,ca, b, c — стороны треугольника;
rr — радиус вписанной в треугольник окружности.
Пусть радиус вписанной окружности равен 2 (см.). Длины сторон возьмем из предыдущей задачи.
Решение
a=3a=3
b=4b=4
c=5c=5
r=2r=2
p=3+4+52=6p=frac{3+4+5}{2}=6
S=6⋅2=12S=6cdot 2=12 (см. кв.)
Ответ: 12 (см. кв.)
Формула площади треугольника по двум сторонам и углу между ними
S=12⋅b⋅c⋅sin(α)S=frac{1}{2}cdot bcdot ccdotsin(alpha),
b,cb, c — стороны треугольника;
αalpha — угол между сторонами bb и cc.
Стороны треугольника равны 5 (см.) и 6 (см.), угол между ними равен 30 градусов. Найти площадь треугольника.
Решение
b=5b=5
c=6c=6
α=30∘alpha=30^{circ}
S=12⋅5⋅6⋅sin(30∘)=7.5S=frac{1}{2}cdot 5cdot 6cdotsin(30^{circ})=7.5 (см. кв.)
Ответ: 7.5 (см. кв.)
Контрольная по геометрии недорого на сервисе Студворк от профильных экспертов!
