Как найти площадь треугольника через синусы углов

По формуле площади треугольника через синус угла

Правило

Формула площади треугольника через синус угла

В треугольнике (displaystyle ABC) (displaystyle S_{ABC}=frac{1}{2}cdot red{AB} cdot color {blue}{BC}cdot sin angle color {#339900}{B}{small .})

(displaystyle S_{ABC}=frac{1}{2}cdot {AB} cdot {BC}cdot sinangle {ABC}{small .})

Так как (displaystyle AB=15 {small,}) (displaystyle BC=8sqrt{2} {small,}) (displaystyle angle ABC= 45^{circ} {small ,})  то 

(displaystyle S_{ABC}=frac{1}{2}cdot {15} cdot {8sqrt{2}}cdot sin 45^{circ}={60sqrt{2}}sin 45^{circ}{small .})

Поскольку (displaystyle sin 45^{circ} =frac {sqrt{2}}{2}{small ,}) то 

(displaystyle S_{ABC}={60sqrt{2}}sin 45^{circ}=60sqrt{2}cdot frac {sqrt{2}}{2}=60{small .})

Ответ: (displaystyle 60{small.})

Всем привет, сегодня я покажу как выводятся 4-основные формулы для нахождения площади треугольника, для понимания следующего материала нужно знать теорему синусов, площадь прямоугольника.

*UDP доказательство формулы Герона в этой статье*

Для начала поймем один частный случай(если это понимаете, пролистывайте дальше).

Площадь прямоугольного треугольника.

У нас есть прямоугольный треугольник с катетами a,b, нужно найти его площадь.

Достраиваем до прямоугольника.

Площадь такого прямоугольника будет a * b, а значит площадь прямоугольного треугольника будет 1/2 * a * b(т.е. половинка от площади прямоугольника).

Этот факт нам понадобится для доказательства первой формулы.

Площадь треугольника через основание и высоту.

Мы опустили высоту на основание a, замечаем что исходный треугольник разбился на два прямоугольный треугольника, значит посчитаем их площадь, но для начала назовём отрезки x, y , на которые высота делит основание a.

Найдем площадь 1,2 треугольника и сложим их(т.к он и состоит из этих площадей).

А теперь вот здесь выносим общий множитель за скобку.

x + y – это и есть a, => получаем формулу половина основания на высоту.

Площадь через синус угла между сторонами.

Опустим высоту на основание b и назовём её x. Посмотрим на этот прямоугольный треугольник

Нам нужно найти x, как это можно сделать если нам известен только угол альфа и гипотенуза a? Очевидно, расписать синус этого угла и выразить от туда x.

Ну и теперь используем ранее доказанную формулу “половина основания на высоту”.

Произведение всех сторон на 4 радиуса описанной окружности.

Чтобы доказать эту формулу, нужно знать теорему синусов. и помнить ранее доказанную формулу.

Выразим синус угла альфа из теоремы синусов.

Подставляем синус альфа в ранее доказанную формулу.

Вот и вся формула. Изи, не правда ли? Теперь чуть посложнее.

Площадь треугольника через полупериметр и радиус вписанной окружности.

У нас есть треугольник ABC со сторонами a,b,c , в него вписана окружность радиуса r с центром O, которая касается сторон в точках K, L, M.

Проведём радиус в точки касания и соединим вершины треугольника с центром окр.

Теперь считаем площадь вот этих трех выделенных треугольников

Площадь AOC = 1/2 r * a, AOB = 1/2 r * b, COB = 1/2 r * c.

значит площадь ABC = AOC + AOB + COB

1/2 * r выносим за скобки.

(a + b + c )/ 2 это полупериметр p.

Вот и наша формула.

Если хотите узнать доказательство формулы Герона, заходите на эту статью.

Спасибо за внимание.

Площадь треугольника через синус угла

Если вам необходимо вычислить площадь треугольника через синус угла, тогда вы зашли именно по адресу, потому что сегодня мы детально изучим этот вопрос.

Подобный род задач достаточно распространен в геометрии и, несмотря на свою простоту, неправильное использование формулы может привести к неверному результату.

В общем случае площадь треугольника можно вычислить по формуле: половина произведения двух сторон на синуса угла между ними.

Формулы площади треугольника через синус угла:

Схематическое изображение треугольника:

Где b, с, а – стороны треугольника;

γ, α, β – углы между сторонами.

Если известна только одна сторона и величины всех трех углов, тогда площадь можно найти как:

Площадь равнобедренного треугольника через синус:

здесь a = c,

β – угол между a и c,

α – угол между a и b.

Как можно было увидеть вышеуказанная формула ничем не отличается от общей.

Площадь прямоугольного треугольника через синус:

Где а,b,с – стороны треугольника

А,В,С – углы между сторонами.

Пример задачи

Рассмотрим задачу, в которой известно размеры двух сторон треугольника, а также величина угла между ними. Таким образом, мы можем определить площадь треугольника, которая находится как половина произведения двух сторон и синуса угла между ними.

Определение

Площадь треугольника через синус — это площадь треугольника,
выраженная через две любые стороны треугольника и синус угла между ними.

Синус угла — это число, которое используется для нахождения
разных величин в треугольниках, его можно найти в специальных таблицах.

Введение

Площадь треугольника кроме половины произведения высоты
на основания, можно также найти и другим способом.
Мало кто знает, но через синусы углов можно найти обычно
не только стороны, но и площадь любого треугольника!

Площадь треугольника выраженная без синуса численно равна
половине произведения двух сторон друг на друга
на синус угла между ними.

Площадь треугольника через синус ищется только в том случае,
если по другой формуле площадь треугольника найти нельзя.

Теорема

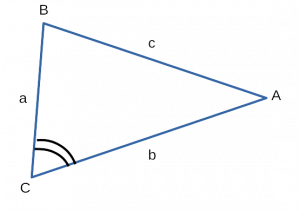
( S = frac{1}2 * BC * AC * sin angle BCA )​

Площадь произвольного треугольника равна полусумме
произведения двух любых сторон треугольника друг на друга,
и на синус угла между этими сторонами.

Формула

[ S = frac{1}2 * a * b * sin α ]

Где a, b — две стороны треугольника, синус α — синус угла α.

Пример

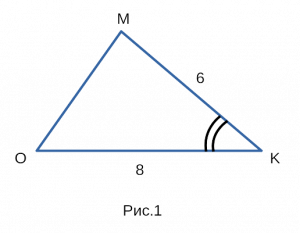
Для примера, возьмем треугольник omk, изображенный на рисунке 1, со сторонами om, mk, ok.
Известно, что mk равен 6, ok равен 8, синус угла okm равен 1/4.

Нужно найти площадь треугольника omk.

Дано:  △omk, mk = 6, ok = 8, sin okm = 1/4.

Найти: S △omk — ?

Решение:

1) ​( S = frac{1}2*a*b*sin α )​​( implies )​( S = frac{1}2*mk*ok*sin okm )​

2) S = 1/2 * 6 * 8 * 1/4 = 1/2 * 6 * 8 * 0.25 = 1/2 * 48 * 0.25 = 1/2 * 12 = 6

Ответ: Площадь треугольника omk равна 6.

Доказательство

Докажем, что площадь произвольного треугольника
равна полусумме произведения двух любых сторон
друг на друга, и на синус угла между этими сторонами.

Чтобы вам наглядно было видно, как мы доказываем,
используем один из известнейших треугольников — египетский треугольник.
Высота в египетском треугольнике равна длине одного из катетов.
Построим прямоугольный треугольник, изображенный на рисунке 2,
со сторонами 3,4,5 с одним из углов 90 градусов.

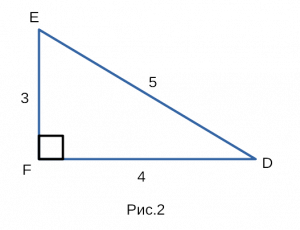
Первым делом найдем площадь обычной формулой,
затем с помощью синуса. Площадь равна половине
основания на высоту — ½3*4 = 6. Теперь найдем с
помощью синуса: ½3*4*sin90 = 6 * 1 = 6. Как видим,
полученные значения площадей сходятся, соответственно
через синус можно найти площадь треугольника ч.т.д.

Теперь, чтобы найти площадь треугольника нам не нужно
знать основание и высоту, можно знать только
две стороны и синус угла между ними.

Заключение

В заключение, можно сказать, что площадь
треугольника можно найти разными способами.
Например, в прямоугольном треугольнике площадь
рассчитать легче чем в любом другом треугольнике,
так как высота уже известна. Именно поэтому,
в школьном курсе, отчасти так подробно изучаются
прямоугольные треугольники. В Древнем Египте были
распространены прямоугольные треугольники со
сторонами 3,4,5; 6,8,10; 5,12,13. Длины этих прямоугольных
треугольников треугольников целые, что значительно,
упрощало разного рода вычисления.

Формулу площади треугольника делает универсальной то,
что она может применена к абсолютно любым треугольникам.
Главное, чтобы были известные две стороны,
и угол или синус угла между ними.

Формула площади треугольника через синус — универсальна,
поэтому может быть применена к любым видам треугольников.