Как найти площадь треугольника если дано основание

По формуле Герона

Формула Герона для нахождения площади треугольника:

– полупериметр треугольника; a,b,c – стороны треугольника.

Через основание и высоту

Формула нахождения площади треугольника с помощью половины его основания и высоту:

a – основание треугольника; h – высота треугольника.

Через две стороны и угол

Формула нахождения площади треугольника через две стороны и угол между ними:

a,b – стороны треугольника; α – угол между сторонами.

Через сторону и два прилежащих угла

Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
<

a– сторона треугольника; α и β – прилежащие углы.

Площадь прямоугольного треугольника

Прямоугольный треугольник – треугольник у которого один из углов прямой, т.е. равен 90°.

Формула нахождения площади прямоугольного треугольника через катеты:

a, b – катеты треугольника.

Площадь равнобедренного треугольника через стороны

Равнобедренный треугольник – треугольник, в котором две стороны равны. А значит, равны и два угла.

Формула нахождения площади равнобедренного треугольника через две стороны:

a, b – стороны треугольника.

Площадь равнобедренного треугольника через основание и угол

Формула нахождения площади равнобедренного треугольника через основание и угол:

a – основание равнобедренного треугольника; α – угол между сторонами.

Площадь равностороннего треугольника через стороны

Равносторонний треугольник – треугольник, в котором все стороны равны, а каждый угол равен 60°.

Формула нахождения площади равностороннего треугольника через сторону:

a – сторона равностороннего треугольника.

Площадь равностороннего треугольника через высоту

Формула нахождения площади равностороннего треугольника через высоту:

h – высота равностороннего треугольника.

Площадь равностороннего треугольника через радиус вписанной окружности

Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:

r – радиус вписанной окружности равностороннего треугольника.

Площадь равностороннего треугольника через радиус описанной окружности

Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:

r – радиус описанной окружности равностороннего треугольника.

Площадь треугольника через радиус описанной окружности и три стороны

Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:

a, b, c – стороны треугольника; r – радиус описанной окружности треугольника.

Площадь треугольника через радиус вписанной окружности и три стороны

Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:

p – полупериметр треугольника;a, b, c – стороны треугольника; r – радиус вписанной окружности треугольника.

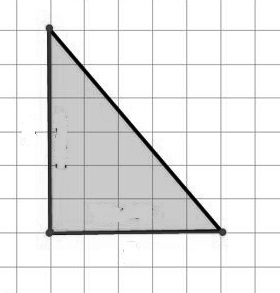
Найти площадь треугольника на рисунке ниже, если клетка имеет площадь, равную единице

Решение.

Очевидно, что одна из сторон треугольника является диагональю прямоугольника, у которого одна сторона имеет длину $5$ (так как $5$ клеток), а вторая $6$ (так как $6$ клеток). Следовательно, площадь этого треугольника будет равняться половине такого прямоугольника. Площадь прямоугольника равняется

$5cdot 6=30$

Тогда площадь треугольника равняется

$30:2=15$

Ответ: $15$.

Площадь треугольника можно найти как половину произведения длины стороны, на высоту, проведенную к этой стороне.

Математически это выглядит следующим образом

$S=frac{1}{2}αh$

где $a$ – длина стороны, $h$ – высота, проведенная к ней.

Доказательство.

Рассмотрим треугольник $ABC$, в котором $AC=α$. К этой стороне проведена высота $BH$, которая равняется $h$. Достроим его до квадрата $AXYC$ как на рисунке 2.

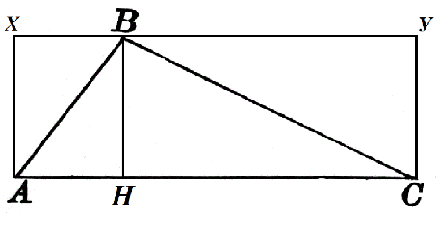
Площадь прямоугольника $AXBH$ равняется $hcdot AH$, а прямоугольника $HBYC$ равняется $hcdot HC$. Тогда

$S_ABH=frac{1}{2}hcdot AH$, $S_CBH=frac{1}{2}hcdot HC$

Следовательно, искомая площадь треугольника, по свойству 2, равняется

$S=S_ABH+S_CBH=frac{1}{2}hcdot AH+frac{1}{2}hcdot HC=frac{1}{2}hcdot (AH+HC)=frac{1}{2}αh$

Теорема доказана.

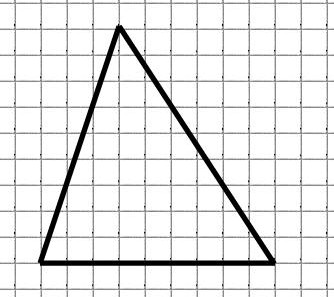
Найти площадь треугольника на рисунке ниже, если клетка имеет площадь, равную единице

Решение.

Основание этого треугольника равняется $9$ (так как $9$ составляет $9$ клеток). Высота также равняется $9$. Тогда, по теореме 1, получим

$S=frac{1}{2}cdot 9cdot 9=40,5$

Ответ: $40,5$.

Если нам даны три стороны треугольника $α$, $β$ и $γ$, то его площадь можно найти следующим образом

$S=sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}$

здесь $ρ$ означает полупериметр этого треугольника.

Доказательство.

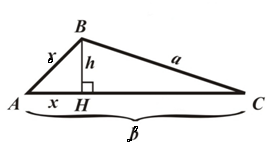
Рассмотрим следующий рисунок:

По теореме Пифагора из треугольника $ABH$ получим

$h^2=γ^2-x^2$

Из треугольника $CBH$, по теореме Пифагора, имеем

$h^2=α^2-(β-x)^2$

$h^2=α^2-β^2+2βx-x^2$

Из этих двух соотношений получаем равенство

$γ^2-x^2=α^2-β^2+2βx-x^2$

То есть

$x=frac{γ^2-α^2+β^2}{2β}$

Получим

$h^2=γ^2-(frac{γ^2-α^2+β^2}{2β})^2$

$h^2=frac{(α^2-(γ-β)^2 )((γ+β)^2-α^2)}{4β^2}$

$h^2=frac{(α-γ+β)(α+γ-β)(γ+β-α)(γ+β+α)}{4β^2}$

Так как $ρ=frac{α+β+γ}{2}$, то $α+β+γ=2ρ$, значит

$h^2=frac{2ρ(2ρ-2γ)(2ρ-2β)(2ρ-2α)}{4β^2}$

$h^2=frac{4ρ(ρ-α)(ρ-β)(ρ-γ)}{β^2 }$

$h=sqrt{frac{4ρ(ρ-α)(ρ-β)(ρ-γ)}{β^2}}$

$h=frac{2}{β}sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}$

По теореме 1, получим

$S=frac{1}{2} βh=frac{β}{2}cdot frac{2}{β} sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}=sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}$

Теорема доказана.

Площадь равностороннего треугольника определяется как произведение квадрата стороны с числом $frac{sqrt{3}}{4}$.

Математически это выглядит следующим образом

$S=frac{α^2sqrt{3}}{4}$

где $α$ – сторона треугольника.

Доказательство.

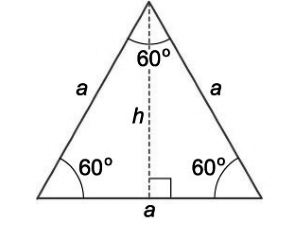
Пусть нам дан равносторонний треугольник, у которого сторона равняется $α$. Проведем высоту $h$ (рис. 5).

Высота равностороннего треугольника является также и медианой, значит, по теореме Пифагора

$h^2=α^2-frac{α^2}{4}$

$h^2=frac{3}{4} α^2$

$h=frac{αsqrt{3}}{2}$

Значит по теореме 1:

$S=frac{α^2sqrt{3}}{4}$

Теорема доказана.

Найти площадь равностороннего треугольника, если его сторона равняется $2$.

Решение.

Используя теорему 3, получим

$S=frac{4sqrt{3}}{4}=sqrt{3}$

Ответ: $sqrt{3}$.