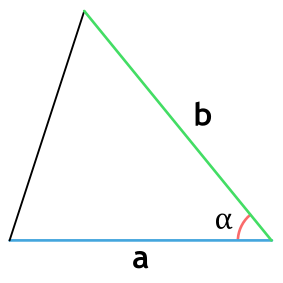
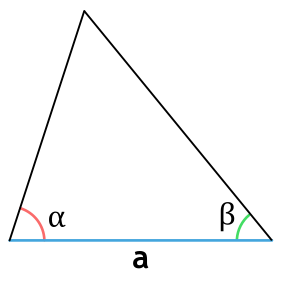
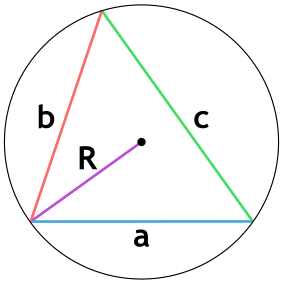
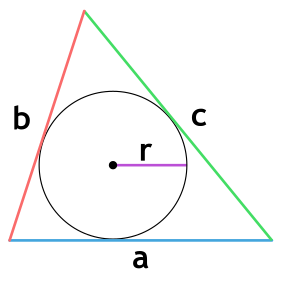
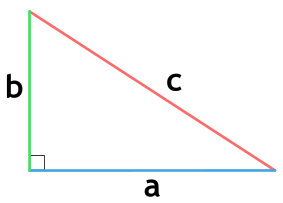
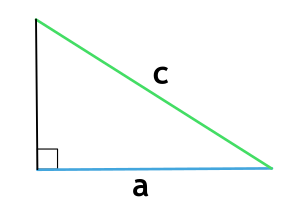
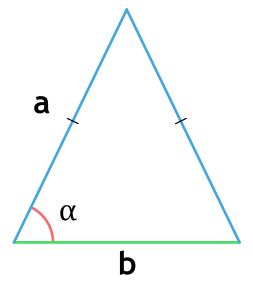
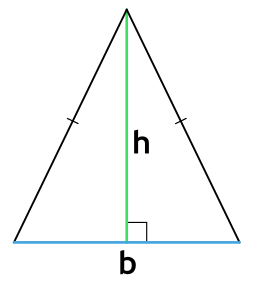
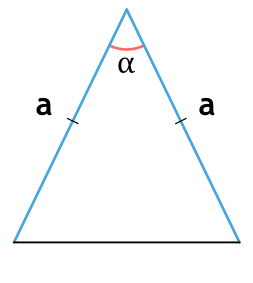
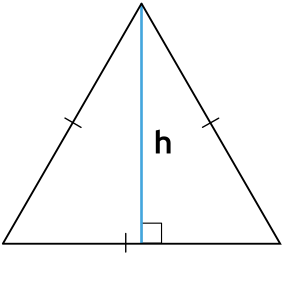
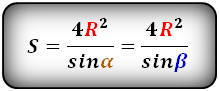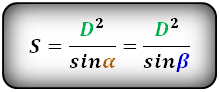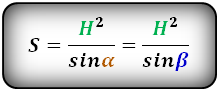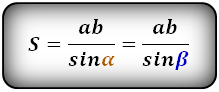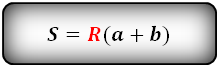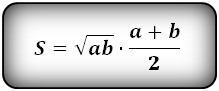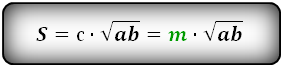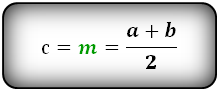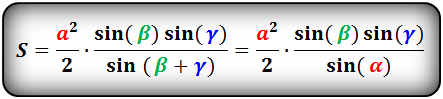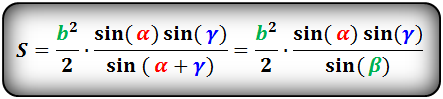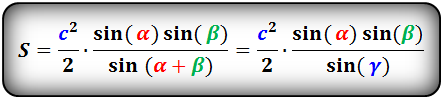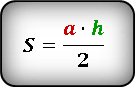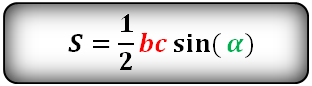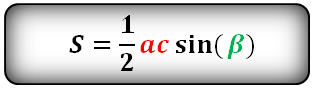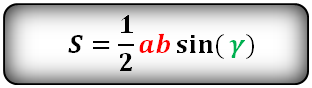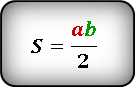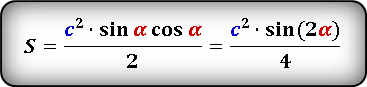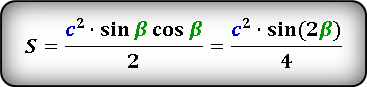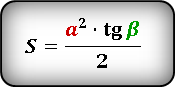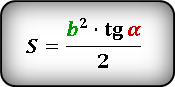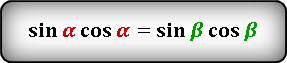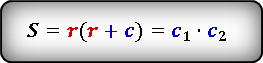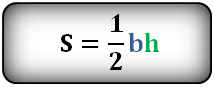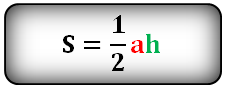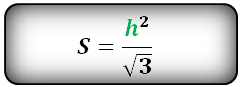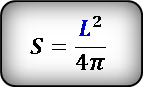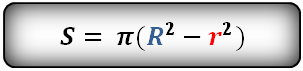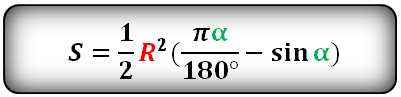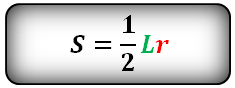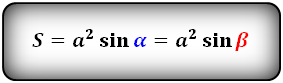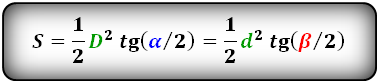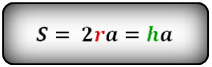Площадь треугольника через тангенс
Площадь равнобедренного треугольника — формулы вычисления
Площадь равнобедренного треугольника важна для вычисления многих геометрических и математических задач. Например, определение площади любого многоугольника связано с его разделением на ряд треугольников и расчетом площади каждого из них.
Геометрическое тело, обладающее двумя равными сторонами и углами – есть частный случай простого разностороннего многоугольника.
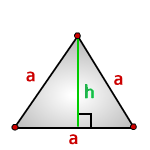
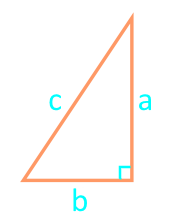
Каждая из идентичных линий называется боковой, а третья – основанием.
Если в таком треугольнике опустить среднюю линию из его вершины на 3-ю сторону, то образовавшиеся два плоских тела будут идентичны (так как имеют все признаки подобия).
Площадь (S) фигуры с тремя углами возможно установить:
по двум сторонам и высоте;
через угол между двумя сторонами и величину одной из них;
по двум сторонам;
через синус противолежащего основанию угла;
зная синус прилежащего угла и др.
Площадь равнобедренного треугольника через высоту
Вычисление площади треугольника с использованием его высоты и параметров основания – самый актуальный вариант, на базе которого строятся многие другие методы решения.
У планиметрической фигуры с двумя тождественными углами и боковыми отрезками высота может рассматриваться, как медиана и биссектриса. То есть линия, проведенная из вершины, делит планиметрический объект на два эквивалентных прямоугольных треугольника.
И общая их площадь сводится к:
b — размер основания;
Требуется рассчитать S тупоугольного равнобедренного многоугольника. Его h=3 см, а длина b = 8 см.
Вычисления выглядят следующим образом:
Площадь равнобедренного треугольника через стороны
Найти S планиметрического тела с двумя одинаковыми чертами, зная их параметры, возможно.
Для этого необходима теорема Пифагора, формулы которой видны на картинке,
и формула для отыскания S через биссектрису S = ½ * b * h.
После проведения медианы к середине 3-его отрезка, в равнобедренном треугольнике образуются 2 единообразных плоских тела с h между 2-мя катетами.
Таким образом, используя свойство сторон прямоугольного треугольника, выводим формулу, которая показана на картинке:
При высчитывание S равностороннего треугольника это выражение примет другой вид. Сравнить формулы нахождения площади равностороннего и равнобедренного треугольников можно, взглянув на картинку:
У остроугольного равнобедренного треугольника даны габариты боковины b = 3 см и базиса a = 2 см. Надлежит найти его S:
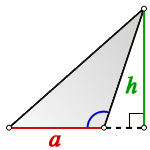
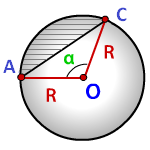
Площадь равнобедренного треугольника через синус угла
В геометрии встречаются задания по отысканию площади многоугольника с тремя схожими краями через данный угол и длину прилегающей стороны.
В этой ситуации определение размера h будет осуществляться с использованием угла, прилегающего к измеренной грани. Таким образом выводится выражение, которое хорошо иллюстрирует следующая картинка:
Посмотрим на рисунок, приведенный выше. Известно, что ∠ACB фигуры 30 градусов, а величина его боковой стороны AC = AB равняется 4 см. Требуется вычислить её S.
Формула площади равнобедренного треугольника через тангенс угла
Как правило, в планиметрии нередко встречаются задания по нахождению S треугольника, в котором определено значение стороны и угол.
Разнообразные равенства для решения задач, в том числе и нахождения S через тангенс угла, можно увидеть ниже:
Дан равнобедренный треугольник OPQ (см. рис. 1). Известны величины: основание OQ = 5 см и угол QOP = 45 0 . Требуется найти площадь треугольника OPQ.
Прежде всего посмотрим, как найти нам требуемую величину и какую применить формулу. Остановим свой выбор на формуле нахождения площади S по тангенсу угла.
Зная, что у нас равнобедренный треугольник, у которого углы у основания равны, найдем третий угол:
180 — 45 — 45 = 90 0 — угол OPQ.
SOPQ = 5 2 /4 * tg 45° = 25/4 * 1 = 6, 25 см 2
Вот так, используя прежде всего знания о свойствах фигур, можно получать самые разнообразные способы вычисления той величины, какая требуется в задаче.
Как найти площадь треугольника – все способы от самых простых до самых сложных
Зависит от того, какой треугольник.
Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.
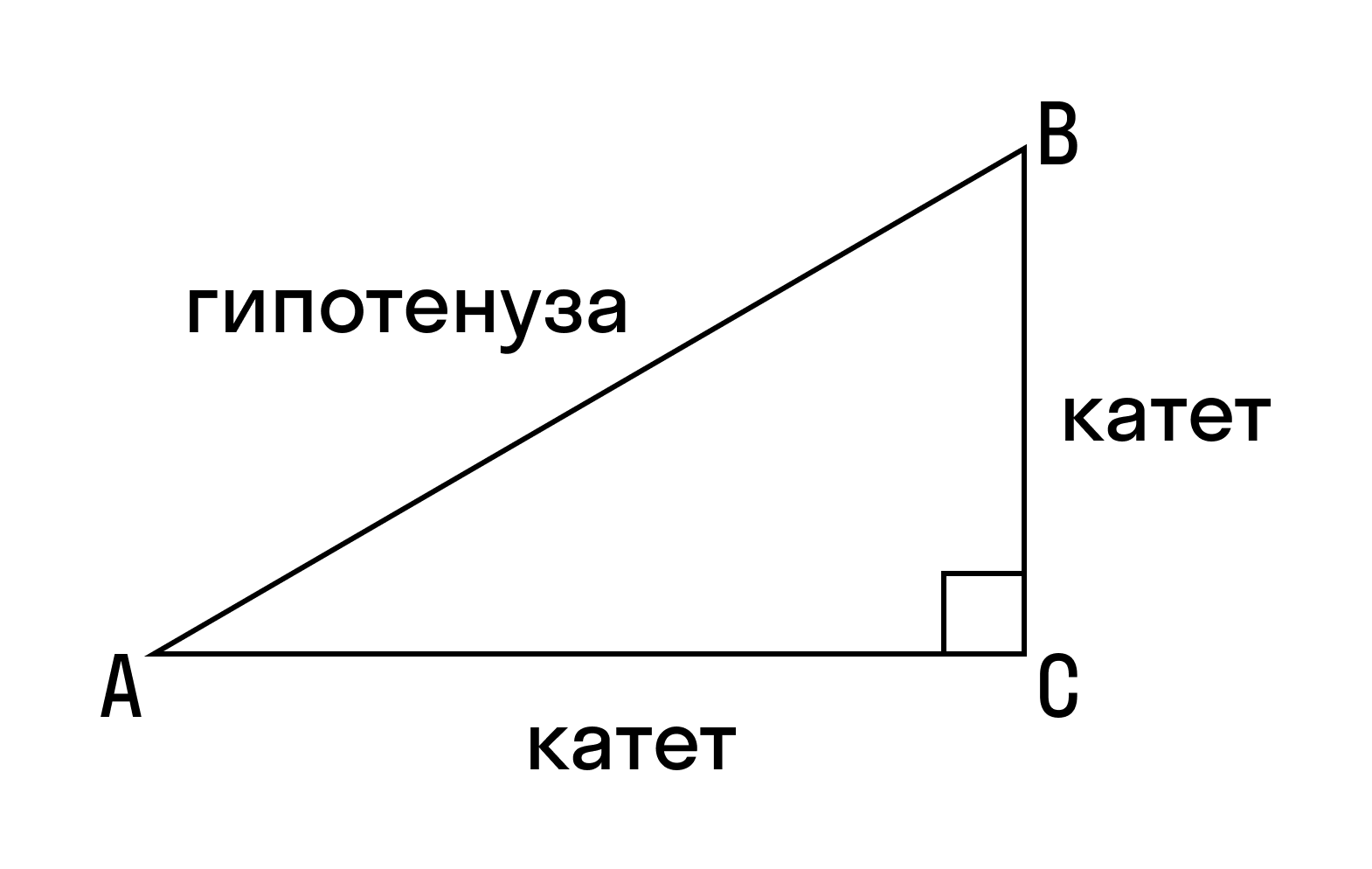
Если треугольник прямоугольный
То есть один из его углов равен 90 градусам.
Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.
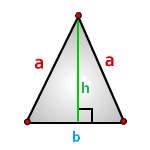
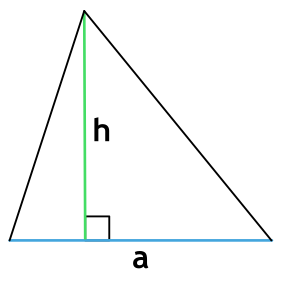
Если он равнобедренный
То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.
Если он равносторонний
То есть все три стороны равны. Ваши действия такие:
- Найдите квадрат стороны – умножьте эту сторону на нее же. Если у вас сторона равна 4, умножьте 4 на 4, будет 16.
- Умножьте полученное значение на корень из 3. Это примерно 1,732050807568877293527.
- Поделите все на 4.
Если известна сторона и высота
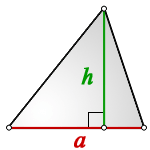
Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.
Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.
Если известны две стороны и градус угла между ними
Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:
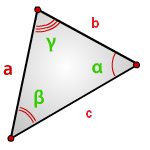
Если известны длины трех сторон
- Найдите периметр. Для этого сложите все три стороны.
- Найдите полупериметр – разделите периметр на два. Запомните значение.
- Отнимите от полупериметра длину первой стороны. Запомните.
- Отнимите от полупериметра длину второй стороны. Тоже запомните.
- Отнимите от полупериметра длину третьей стороны. И ее запомните.
- Умножьте полупериметр на каждое из этих чисел (разницу с первой, второй и третьей стороной).
- Найдите квадратный корень.
Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.
Если известны три стороны и радиус описанной окружности
Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.
Если известны три стороны и радиус вписанной окружности
Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.
Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.
Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.
Площадь прямоугольного треугольника
О чем эта статья:
площадь, 8 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные определения
Прямоугольный треугольник — это треугольник, в котором один угол прямой, то есть равен 90˚.
Гипотенуза — это сторона, противолежащая прямому углу.
Катеты — это стороны, прилежащие к прямому углу.
Чтобы найти площадь прямоугольного треугольника, можно применить любую формулу нахождения площади треугольника — их несколько.
Формула для нахождения площади прямоугольного треугольника через катеты
Чтобы найти площадь, нужно вывести формулу:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию.
Так как в прямоугольном треугольнике катеты перпендикулярны, то один катет — это высота, проведенная ко второму катету.
Отсюда следует, что площадь прямоугольного треугольника равна половине произведения его катетов.
Используйте эту формулу, чтобы найти площадь прямоугольного треугольника через катеты.
S = 1/2 (a × b), где a и b — катеты
Формула для нахождения площади прямоугольного треугольника через гипотенузу
Площадь прямоугольного треугольника равна половине произведения гипотенузы на высоту, проведенную к гипотенузе.
где с — гипотенуза,
Используйте эту формулу, чтобы найти площадь прямоугольного треугольника через гипотенузу.
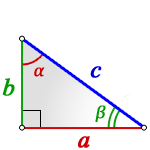
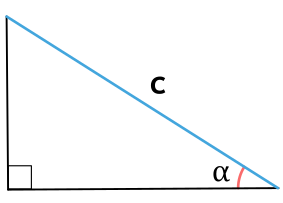
Формула для нахождения площади прямоугольного треугольника через гипотенузу и острый угол
α, β — острые углы
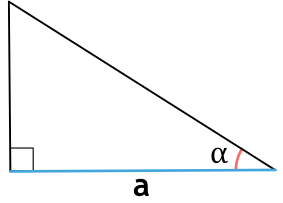
Формулы нахождения площади прямоугольного треугольника через катет и угол
α, β — острые углы
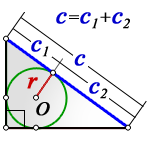
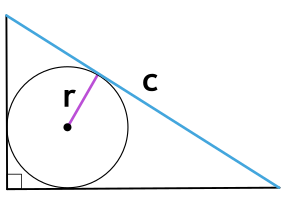
Формулы нахождения площади прямоугольного треугольника через радиус вписанной окружности и гипотенузу
Радиус вписанной окружности выражается через катеты и гипотенузу по формуле:
S прямоугольного треугольника = r (r + c) = c1 × c2
r — радиус вписанной окружности
C1 и С2 — отрезки, полученные делением гипотенузы на две части точкой касания с окружностью
Уверены, что во всем разобрались? Закрепите знания на курсах обучения математике в онлайн-школе Skysmart!
Площадь равнобедренного треугольника — формулы вычисления
Площадь равнобедренного треугольника важна для вычисления многих геометрических и математических задач. Например, определение площади любого многоугольника связано с его разделением на ряд треугольников и расчетом площади каждого из них.
Геометрическое тело, обладающее двумя равными сторонами и углами – есть частный случай простого разностороннего многоугольника.
Каждая из идентичных линий называется боковой, а третья – основанием.
Если в таком треугольнике опустить среднюю линию из его вершины на 3-ю сторону, то образовавшиеся два плоских тела будут идентичны (так как имеют все признаки подобия).
Площадь (S) фигуры с тремя углами возможно установить:
по двум сторонам и высоте;
через угол между двумя сторонами и величину одной из них;
по двум сторонам;
через синус противолежащего основанию угла;
зная синус прилежащего угла и др.
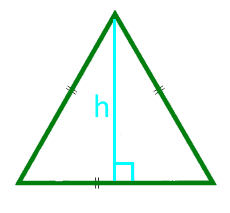
Площадь равнобедренного треугольника через высоту
Вычисление площади треугольника с использованием его высоты и параметров основания – самый актуальный вариант, на базе которого строятся многие другие методы решения.
У планиметрической фигуры с двумя тождественными углами и боковыми отрезками высота может рассматриваться, как медиана и биссектриса. То есть линия, проведенная из вершины, делит планиметрический объект на два эквивалентных прямоугольных треугольника.
И общая их площадь сводится к:
b — размер основания;
Требуется рассчитать S тупоугольного равнобедренного многоугольника. Его h=3 см, а длина b = 8 см.
Вычисления выглядят следующим образом:
Площадь равнобедренного треугольника через стороны
Найти S планиметрического тела с двумя одинаковыми чертами, зная их параметры, возможно.
Для этого необходима теорема Пифагора, формулы которой видны на картинке,
и формула для отыскания S через биссектрису S = ½ * b * h.
После проведения медианы к середине 3-его отрезка, в равнобедренном треугольнике образуются 2 единообразных плоских тела с h между 2-мя катетами.
Таким образом, используя свойство сторон прямоугольного треугольника, выводим формулу, которая показана на картинке:
При высчитывание S равностороннего треугольника это выражение примет другой вид. Сравнить формулы нахождения площади равностороннего и равнобедренного треугольников можно, взглянув на картинку:
У остроугольного равнобедренного треугольника даны габариты боковины b = 3 см и базиса a = 2 см. Надлежит найти его S:
Площадь равнобедренного треугольника через синус угла
В геометрии встречаются задания по отысканию площади многоугольника с тремя схожими краями через данный угол и длину прилегающей стороны.
В этой ситуации определение размера h будет осуществляться с использованием угла, прилегающего к измеренной грани. Таким образом выводится выражение, которое хорошо иллюстрирует следующая картинка:
Посмотрим на рисунок, приведенный выше. Известно, что ∠ACB фигуры 30 градусов, а величина его боковой стороны AC = AB равняется 4 см. Требуется вычислить её S.
Формула площади равнобедренного треугольника через тангенс угла
Как правило, в планиметрии нередко встречаются задания по нахождению S треугольника, в котором определено значение стороны и угол.
Разнообразные равенства для решения задач, в том числе и нахождения S через тангенс угла, можно увидеть ниже:
Дан равнобедренный треугольник OPQ (см. рис. 1). Известны величины: основание OQ = 5 см и угол QOP = 45 0 . Требуется найти площадь треугольника OPQ.
Прежде всего посмотрим, как найти нам требуемую величину и какую применить формулу. Остановим свой выбор на формуле нахождения площади S по тангенсу угла.
Зная, что у нас равнобедренный треугольник, у которого углы у основания равны, найдем третий угол:
180 — 45 — 45 = 90 0 — угол OPQ.
SOPQ = 5 2 /4 * tg 45° = 25/4 * 1 = 6, 25 см 2
Вот так, используя прежде всего знания о свойствах фигур, можно получать самые разнообразные способы вычисления той величины, какая требуется в задаче.
Формулы (тождества) синус, косинус, тангенс, котангенс тройного угла
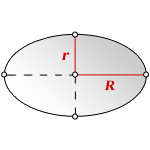
R – большая полуось
r – малая полуось
π ≈ 3.14
Формула площади эллипса, через полуоси:
Калькулятор, вычислить площадь элипса:
1. Формула площади равнобедренной трапеции через стороны и угол
а – нижнее основание
b – верхнее основание
с – равные боковые стороны
α – угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, ( S ):
Формула площади равнобедренной трапеции через стороны и угол, ( S ):
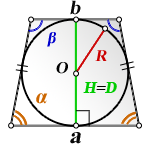
2. Формулы площади равнобедренной трапеции если в нее вписана окружность
R – радиус вписанной окружности
D – диаметр вписанной окружности
O – центр вписанной окружности
H – высота трапеции
α , β – углы трапеции
а – нижнее основание
b – верхнее основание
Формула площади равнобедренной трапеции через радиус вписанной окружности, ( S ):
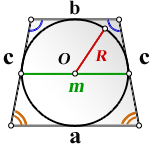
СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:
R – радиус вписанной окружности
m – средняя линия
O – центр вписанной окружности
c – боковые стороны
а – нижнее основание
b – верхнее основание
Формула площади равнобедренной трапеции через радиус вписанной окружности, стороны и среднюю линию ( S ):
СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:
3. Формула площади равнобедренной трапеции через диагонали и угол между ними
d – диагональ трапеции
α , β – углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, ( S ):
4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
c – боковая сторона
m – средняя линия трапеции
α , β – углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, ( S ):
5. Формула площади равнобедренной трапеции через основания и высоту
a – нижнее основание
b – верхнее основание
h – высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, ( S ):
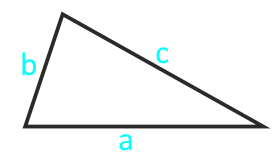
a , b , c – стороны треугольника
α , β , γ – противолежащие углы
Площадь треугольника через сторону и два угла (S):
Формулы для треугольника:
Зная длины всех трех сторон
и используя формулу Герона можно найти площадь разностороннего треугольника
a , b , c – стороны треугольника
p – полупериметр, p=( a + b + c )/2
Формула ( Герона ) площади треугольника через полупериметр ( S ):

Калькулятор – вычислить, найти площадь треугольника:
Формулы для треугольника:
Треугольник это плоская фигура, которая имеет три стороны и три угла. Сумма всех трех углов, равна 180 градусов.
Высота треугольника это – опущенный перпендикуляр из вершины угла на противоположенную сторону или ее продолжение, которую в этом случае, называют основанием.
Что бы найти площадь треугольника,
для этого надо основание умножить на высоту и разделить на два
1. Площадь разностороннего треугольника
h – высота треугольника
Формула площади треугольника (S):
Калькулятор для расчета площади треугольника
2. Площадь треугольника с тупым углом
h – высота треугольника
Формула площади треугольника с тупым углом (S):
Формулы для треугольника:
Зная у треугольника
две стороны и синус угла между ними, находим по формуле, его площадь
a , b , c – стороны треугольника
α , β , γ – углы
Формулы площади треугольника, через две стороны и угол между ними, (S):
Калькулятор – вычислить, найти площадь треугольника:
Формулы для треугольника:
Прямоугольный треугольник, так же как и любой другой треугольник, имеет три стороны и три угла. Разница только в том, что один угол прямой, т. е. 90 градусов и два остальных, острых угла в сумме составляют, тоже 90 градусов.
Две стороны, которые формируют прямой угол, называют катетами, а третья сторона напротив прямого угла, называется – гипотенуза
1. Если известны только катеты
a , b – катеты треугольника
Формула площади треугольника через катеты ( S ) :
2. Если известны острый угол и гипотенуза или катет
c – гипотенуза
a , b – катеты
α , β – острые углы
Формулы площади прямоугольного треугольника через гипотенузу и угол ( S ) :
Формулы площади прямоугольного треугольника через катет и угол ( S ) :
Как известно, сумма острых углов в прямоугольном треугольнике равна 90 градусов, а если
то справедливы следующие тождества:
3. Если известны радиус вписанной окружности и гипотенуза
c – гипотенуза
c 1 , c 2 – отрезки полученные делением гипотенузы, точкой касания окружности
r – радиус вписанной окружности
О – центр вписанной окружности
Формулы площади прямоугольного треугольника через радиус вписанной окружности и гипотенузу ( S ) :
b – основание треугольника
a – равные стороны
h – высота
Формула площади треугольника через высоту h и основание b , (S):
Калькулятор – вычислить, найти площадь треугольника через высоту и основание:
Формула площади треугольника через, стороны a , b , (S):

Калькулятор – вычислить, найти площадь треугольника через равные стороны и основание:
b – основание треугольника
a – равные стороны
h – высота
Формулы для треугольника:
Если вы знаете сторону или высоту
вы можете найти площадь равностороннего треугольника
a – сторона треугольника
h – высота
Площадь треугольника через сторону a и высоту h , (S):
Площадь треугольника только через сторону a , (S):
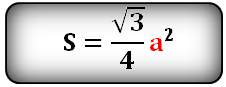
Калькулятор для расчета площади равностороннего треугольника
Площадь треугольника только через высоту h , ( S ):
Калькулятор для расчета площади равностороннего треугольника
a – сторона треугольника
h – высота
Формулы для треугольника:
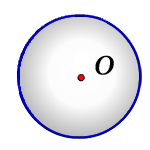
Формула площади круга, диаметр
Круг это плоская фигура, все точки которой, расположены на любом расстоянии от определенной точки (центр круга) но не больше заданной длины (радиус).
Радиус круга – отрезок, соединяющий центр окружности и любую, максимально удаленную от центра точку круга.
Диаметр круга – отрезок, соединяющий две любые точки максимально удаленные от центра круга и проходящий через этот центр. Диаметр, в два раза больше радиуса
или радиус круга или длину окружности, можно найти его площадь.
r – радиус круга
D – диаметр круга
Формула площади круга, (S):
на тему: Площадь круга
Калькулятор для расчета площади круга через радиус
Калькулятор для расчета площади круга через диаметр
L – длина окружности
О – центр круга
Формула площади круга если известна длина окружности, (S):
на тему: Площадь круга
Калькулятор для расчета площади круга через длину
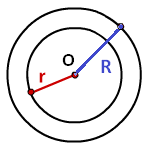
Площадь кольца равна – число π , умноженное на разницу квадратов, радиуса внешней окружности и радиуса внутренней окружности
R – радиус внешней окружности
r – радиус внутренней окружности
Формула площади кольца (S):
Калькулятор – вычислить, найти площадь кольца
R – радиус внешней окружности
r – радиус внутренней окружности
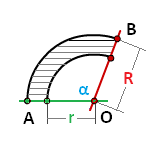
α – угол сектора AOB, в градусах
Формула площади сектора кольца (S):
R – радиус круга
α – угол сегмента в градусах
Формула площади сегмента круга (S), отсекаемая хордой AC :
Калькулятор для расчета длины дуги окружности :
Формулы для окружности и круга:
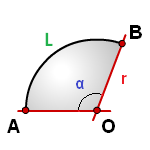
Найти площадь сектора круга если даны радиус и длина дуги или радиус и центральный угол
r – радиус круга
L – длина дуги AB
α – угол сектора круга AOB в градусах
Формула площади сектора круга (S), через длину дуги ( L ):
Формула площади сектора круга (S), через угол ( α ):
Формулы для окружности и круга:
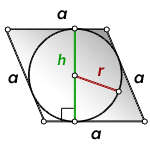
Вычислить площадь ромба, зная: (диагонали) или (сторону и угол между ними) или (диагональ и угол между сторонами)
a – сторона ромба
D – большая диагональ
d – меньшая диагональ
α – острый угол
β – тупой угол
Формулы площади ромба через диагонали и углы между сторонами ( S ):
a – сторона ромба
h – высота
r – радиус вписанной окружности
Формула площади ромба через высоту или радиус вписанной окружности ( S ):
1. Формула площади параллелограмма через стороны и углы
a, b – стороны параллелограмма
α , β – углы параллелограмма
Формула площади через стороны и углы параллелограмма, ( S ):
Калькулятор – вычислить, найти площадь параллелограмма:
2. Формула площади параллелограмма через сторону и высоту
a, b – стороны параллелограмма
H b – высота на сторону b
H a – высота на сторону a
Формула площади через стороны и высоты параллелограмма, ( S ):
3. Формула площади параллелограмма через диагонали и угол между ними
D – большая диагональ
d –меньшая диагональ
α , β – углы между диагоналями
Формула площади через диагонали параллелограмма и угол между ними , ( S ):
Калькулятор – вычислить, найти площадь параллелограмма:
Формулы для параллелограмма:
[spoiler title=”источники:”]
http://sprint-olympic.ru/uroki/geometrija/85090-ploshad-ravnobedrennogo-treygolnika-formyly-vychisleniia.html
http://www-formula.ru/2011-09-21-23-43-54/24-elementgeom/ploshadploskfigur
[/spoiler]
В этой статье собраны наиболее популярные формулы для нахождения площади треугольника.
Как найти площадь треугольника по высоте?
Если известно основание и высота, проведенная к основанию треугольника, можно вычислить площадь треугольника.
(S=frac{1}{2}a*h)
Калькулятор площади треугольника по высоте и основанию
Основание треугольника:
Высота треугольника:
Как найти площадь треугольника: формула Герона
Формула площади треугольника Герона помогает вычислить ее по трем сторонам фигуры:
(S=sqrt{p(p-a)(p-b)(p-c)})
где (a,b,c) – стороны треугольника, (p=frac{a+b+c}{2}) – его полупериметр.
Калькулятор площади треугольника по трем сторонам
Первая сторона треугольника:
Вторая сторона треугольника:
Третья сторона треугольника:
Формула нахождения площади треугольника по окружности
Как вычислить площадь треугольника, если известна окружность и три его стороны?
(S=frac{a*b*c}{4R})
Калькулятор площади треугольника по трем сторонам и радиусу описанной окружности
Первая сторона треугольника:
Вторая сторона треугольника:
Третья сторона треугольника:
Радиус описанной окружности R:
Как найти площадь прямоугольного треугольника
Чтобы найти площадь прямоугольного треугольника, необходимо знать длины двух катетов. После этого можно воспользоваться формулой:
S = (a * b) / 2
, где a и b – длины катетов. Просто перемножьте значения длин катетов и разделите результат на два, чтобы найти площадь прямоугольного треугольника.
Как узнать площадь треугольника по радиусу и полупериметру
Можно найти площадь треугольника, когда мы знаем полупериметр и радиус вписанной окружности:
(S=pr)
где r – радиус вписанной окружности, (p=frac{a+b+c}{2})– его полупериметр.
Калькулятор площади треугольника по трем сторонам и радиусу вписанной окружности
Первая сторона треугольника:
Вторая сторона треугольника:
Третья сторона треугольника:
Радиус вписанной окружности R:
Как найти площадь треугольника по стороне и тангенсу: формула
Формула нахождения площади по стороне и тангенсу углов треугольника:
(S=frac{c^2}{2(ctgA+ctgB)})
Основные формулы площади треугольника для учащихся 5-6 классов
Для ученика 5-6 класса обычно достаточно знать две формулы для вычисления площади треугольника:
-
Формула площади произвольного треугольника по основанию и высоте:
S = (a * h) / 2
где S – площадь треугольника, a – длина основания треугольника, h – высота треугольника, опущенная на это основание.
-
Формула Герона:
S = sqrt(p * (p – a) * (p – b) * (p – c))
где S – площадь треугольника, a, b, c – длины сторон треугольника, p – полупериметр треугольника, равный половине суммы длин сторон:
p = (a + b + c) / 2
Здесь sqrt означает извлечение квадратного корня. Обе формулы могут быть использованы для вычисления площади треугольника в зависимости от имеющихся данных.
Как найти площадь равнобедренного и равностороннего треугольника
Чтобы найти площадь равнобедренного треугольника, необходимо знать длину боковой стороны и высоту, проведенную к основанию. После этого можно воспользоваться формулой:
S = (a * h) / 2
, где a – длина основания, а h – высота, опущенная на основание.
Чтобы найти площадь равностороннего треугольника, необходимо знать длину любой стороны. После этого можно воспользоваться формулой:
S = (a^2 * sqrt(3)) / 4
, где a – длина любой стороны. Также можно использовать формулу через высоту:
S = (a * h) / 2
, где h – высота, опущенная из вершины на основание, а a – длина любой стороны.
Все формулы площади треугольника
Не знаете, как посчитать площадь треугольника? Собрали для вас все возможные формулы. как находить площадь треугольника:
-
Формула площади треугольника по основанию и высоте:
S = (a * h) / 2
где S – площадь треугольника, a – длина основания треугольника, h – высота треугольника, опущенная на это основание.
-
Формула Герона:
S = sqrt(p * (p – a) * (p – b) * (p – c))
где S – площадь треугольника, a, b, c – длины сторон треугольника, p – полупериметр треугольника, равный половине суммы длин сторон:
p = (a + b + c) / 2
-
Формула площади треугольника через две стороны и угол между ними:
S = (a * b * sin(C)) / 2
где S – площадь треугольника, a и b – длины двух сторон треугольника, C – угол между этими сторонами (в радианах), sin – функция синуса.
-
Формула площади треугольника через радиус вписанной окружности:
S = (a * b * c) / (4 * R)
где S – площадь треугольника, a, b, c – длины сторон треугольника, R – радиус вписанной в треугольник окружности.
-
Формула площади треугольника через радиус описанной окружности:
S = (a * b * c) / (4 * R)
где S – площадь треугольника, a, b, c – длины сторон треугольника, R – радиус описанной вокруг треугольника окружности.
Часто задаваемые вопросы
✅ Какие есть формулы площади треугольника?
↪ Формула площади треугольника по основанию и высоте: S = (a * h) / 2
Формула Герона: S = sqrt(p * (p – a) * (p – b) * (p – c)), где p = (a + b + c) / 2
Формула площади треугольника через две стороны и угол между ними: S = (a * b * sin(C)) / 2
Формула площади треугольника через радиус вписанной окружности: S = (a * b * c) / (4 * R)
Формула площади треугольника через радиус описанной окружности: S = (a * b * c) / (4 * R)
✅ Как найти площадь треугольника формуле Герона?
↪ Формула площади треугольника Герона помогает вычислить ее по трем сторонам фигуры.
Больше уроков и заданий по всем школьным предметам в онлайн-школе “Альфа”. Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
Ученик
(9),
закрыт
12 лет назад
сергей соколов
Высший разум
(129034)
13 лет назад
Находим синус угла следующими действиями.
котангенс = 1 / тангенс = 1 / 0,75 = 4/3
1/(синус^2) = 1 + котангенс^2 = 1 + (4/3)^2 = 25/9
синус^2 = 9/25
синус = 3/5
Площадь треугольника равна полупроизведению сторон на синус угла между ними
S = 4 * 6 * 3/5 / 2 = 7,2
Viktor
Просветленный
(49792)
13 лет назад
Есть формула для вычисления площади треугольника за сторонами и синусом угла между ними. У вас есть все необходимое для решения поставленной задачи. Дерзайте, Алина, это пойдет вам только на пользу.

{S = dfrac{1}{2} cdot a cdot h}
Задача нахождения площади треугольника довольно распространена не только в науке, но и в быту. Для вас мы разработали калькулятор для нахождения площади любого треугольника – равнобедренного, равностороннего, прямоугольного или обыкновенного (разностороннего) по 22 формулам.
- Калькулятор площади треугольника
- Площадь треугольника
- через основание и высоту
- через две стороны и угол между ними
- через сторону и два прилежащих угла
- через радиус описанной окружности и 3 стороны
- через радиус вписанной окружности и 3 стороны
- по формуле Герона
- Площадь прямоугольного треугольника
- через катеты
- через гипотенузу и прилежащий угол
- через катет и прилежащий угол
- через радиус вписанной окружности и гипотенузу
- через вписанную окружность
- по формуле Герона
- через катет и гипотенузу
- Площадь равнобедренного треугольника
- через основание и сторону
- через основание, боковую сторону и угол
- через основание и высоту
- через боковые стороны и угол между ними
- через основание и угол между боковыми сторонами
- Площадь равностороннего треугольника
- через сторону
- через высоту
- через радиус описанной окружности
- через радиус вписанной окружности
- Примеры задач
Площадь треугольника
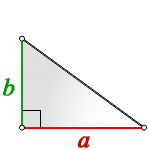
Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.
Площадь треугольника через основание и высоту
{S = dfrac{1}{2} cdot a cdot h}
a – длина основания
h – высота, проведенная к основанию
Площадь треугольника через две стороны и угол между ними
{S = dfrac{1}{2} cdot a cdot b cdot sin(alpha)}
a и b – стороны треугольника
α – угол между сторонами a и b
Площадь треугольника через сторону и два прилежащих угла
{S = dfrac{a^2}{2} cdot dfrac{sin{(alpha)} cdot sin{(beta)}}{sin{(gamma)}}}
{gamma = 180 – (alpha + beta)}
a – сторона треугольника
α и β – прилежащие к стороне a углы
Площадь треугольника через радиус описанной окружности и 3 стороны
{S = dfrac{a cdot b cdot c}{4 cdot R}}
a, b и c – стороны треугольника
R – радиус описанной окружности
Площадь треугольника через радиус вписанной окружности и 3 стороны
{S = r cdot dfrac{a + b + c}{2}}
a, b и c – стороны треугольника
r – радиус вписанной окружности
Площадь треугольника по формуле Герона
{S = sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)}}
{p= dfrac{a+b+c}{2}}
a, b и c – стороны треугольника
p – полупериметр треугольника
Площадь прямоугольного треугольника
Прямоугольный треугольник — это треугольник, в котором один угол прямой (равен 90 градусов).
Площадь прямоугольного треугольника через катеты
{S = dfrac{1}{2} cdot a cdot b}
a и b – стороны треугольника
Площадь прямоугольного треугольника через гипотенузу и прилежащий угол
{S = dfrac{1}{4} cdot c^2 cdot sin{(2 alpha)}}
c – гипотенуза прямоугольного треугольника
α – прилежащий к гипотенузе c угол
Площадь прямоугольного треугольника через катет и прилежащий угол
{S = dfrac{1}{2} cdot a^2 cdot tg{(alpha)}}
a – катет прямоугольного треугольника
α – прилежащий к катету a угол
Площадь прямоугольного треугольника через радиус вписанной окружности и гипотенузу
{S = r cdot (r+c)}
r – радиус вписанной окружности
c – гипотенуза прямоугольного треугольника
Площадь прямоугольного треугольника через вписанную окружность
{S = c_1 cdot c_2}
с1 и с2 – отрезки, полученные делением гипотенузы точкой касания окружности
Площадь прямоугольного треугольника по формуле Герона
{S = (p-a) cdot (p-b)}
{p= dfrac{a+b+c}{2}}
a, b и c – стороны треугольника
p – полупериметр треугольника
Площадь прямоугольного треугольника через катет и гипотенузу
{S = dfrac{1}{2} cdot a cdot sqrt{c^2 – a^2}}
a – катет прямоугольного треугольника
c – гипотенуза прямоугольного треугольника
Площадь равнобедренного треугольника
Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по длине.
Площадь равнобедренного треугольника через основание и сторону
{S = dfrac{b}{4} sqrt{4a^2 – b^2}}
a – боковая сторона равнобедренного треугольника
b – основание равнобедренного треугольника
Площадь равнобедренного треугольника через основание, сторону и угол
{S = dfrac{1}{2} cdot a cdot b cdot sin{(alpha)}}
a – боковая сторона равнобедренного треугольника
b – основание равнобедренного треугольника
α – угол между основанием и боковой стороной
Площадь равнобедренного треугольника через основание и высоту
{S = dfrac{1}{2} cdot b cdot h}
b – основание равнобедренного треугольника
h – высота, проведенная к основанию равнобедренного треугольника
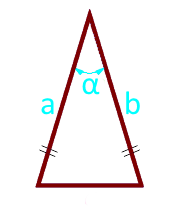
Площадь равнобедренного треугольника через боковые стороны и угол между ними
{S = dfrac{1}{2} cdot a^2 cdot sin(alpha)}
a – боковые стороны равнобедренного треугольника
α – угол между боковыми сторонами
Площадь равнобедренного треугольника через основание и угол между боковыми сторонами
{S = dfrac{b^2}{4 cdot tg {( dfrac{alpha}{2} )}}}
b – основание равнобедренного треугольника
α – угол между боковыми сторонами
Площадь равностороннего треугольника
Равносторонний треугольник – треугольник, у которого все стороны равны.
Площадь равностороннего треугольника через сторону
{S = dfrac{sqrt{3} cdot a^2}{4}}
a – сторона равностороннего треугольника
Площадь равностороннего треугольника через высоту
{S = dfrac{h^2}{sqrt{3}}}
h – высота равностороннего треугольника
Площадь равностороннего треугольника через радиус описанной окружности
{S = dfrac{3 sqrt{3} cdot R^2}{4}}
R – радиус описанной окружности
Площадь равностороннего треугольника через радиус вписанной окружности
{S = 3 sqrt{3} cdot r^2}
r – радиус описанной окружности
Примеры задач на нахождение площади треугольника
Задача 1
Найдите площадь треугольника со сторонами 13 14 15.
Решение
Для решения задачи воспользуемся формулой Герона.
S = sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)}
Для начала нам необходимо найти полупериметр p:
p= dfrac{a+b+c}{2}p= dfrac{13+14+15}{2}= dfrac{42}{2} = 21
Теперь можем подставить его в формулу Герона и найти ответ:
S = sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)} = sqrt{21 cdot (21-13) cdot (21-14) cdot (21-15)} = sqrt{21 cdot (8) cdot (7) cdot (6)} = sqrt{21 cdot 336} = sqrt{7056} = 84 : см^2
Ответ: 84 см²
Убедимся в правильности решения с помощью калькулятора .
Задача 2
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 100.
Решение
Воспользуемся формулой.
S = dfrac{1}{2} cdot a cdot sqrt{c^2 – a^2} = dfrac{1}{2} cdot 28 cdot sqrt{100^2 – 28^2} = dfrac{1}{2} cdot 28 cdot sqrt{10000 – 784} = dfrac{1}{2} cdot 28 cdot sqrt{9216} = dfrac{1}{2} cdot 28 cdot 96 = 14 cdot 96 = 1344 : см^2
Ответ: 1344 см²
Проверим ответ на калькуляторе .
Задача 3
Найдите площадь прямоугольного треугольника если его катет и гипотенуза равны соответственно 15 и 17.
Решение
Задача аналогична предыдущей, поэтому решение очень похоже.
S = dfrac{1}{2} cdot a cdot sqrt{c^2 – a^2} = dfrac{1}{2} cdot 15 cdot sqrt{17^2 – 15^2} = dfrac{1}{2} cdot 15 cdot sqrt{289 – 225} = dfrac{1}{2} cdot 15 cdot sqrt{64} = dfrac{1}{2} cdot 15 cdot 8 = 15 cdot 4 = 60 : см^2
Ответ: 60 см²
Проверка .
Задача 4
Найдите площадь прямоугольного треугольника, если гипотенуза его равна 40 см а острый угол равен 60°.
Решение
Для решения задачи воспользуемся формулой.
S = dfrac{1}{4} cdot c^2 cdot sin{(2 alpha)} = dfrac{1}{4} cdot 40^2 cdot sin{(2 cdot 60°)} = dfrac{1}{4} cdot 1600 cdot sin{(120°)} = 400 cdot dfrac{sqrt{3}}{2} = 200 sqrt{3} : см^2 approx 346.41016 : см^2
Ответ: 200 sqrt{3} : см^2 approx 346.41016 : см^2
Проверка .
Задача 5
Найдите площадь равнобедренного треугольника, если боковая сторона равна 7 см а основание 4 см.
Решение
В этой задаче используем формулу для нахождения площади равнобедренного треугольника через основание и боковую сторону.
S = dfrac{b}{4} sqrt{4a^2 – b^2} = dfrac{4}{4} sqrt{4 cdot 7^2 – 4^2} = sqrt{4 cdot 49 – 16} = sqrt{196 – 16} = sqrt{180} = sqrt{36 cdot 5} = 6sqrt{5} : см^2 approx 13.41641 : см^2
Ответ: 6sqrt{5} : см^2 approx 13.41641
Проверка .
Задача 6
Найдите площадь равнобедренного треугольника, если его основание равно 30, боковая сторона равна 17.
Решение
Решим эту задачу по анологии с предыдущей.
S = dfrac{b}{4} sqrt{4a^2 – b^2} = dfrac{30}{4} sqrt{4 cdot 17^2 – 30^2} = dfrac{30}{4} sqrt{4 cdot 289 – 900} = dfrac{30}{4} sqrt{1156 – 900} = dfrac{30}{4} sqrt{256} = dfrac{30}{4} cdot 16= 30 cdot 4 = 120 : см^2
Ответ: 120 см²
Проверка .
Задача 7
Найдите площадь равностороннего треугольника со стороной 12 см.
Решение
Используем для решения задачи формулу.
S = dfrac{sqrt{3} cdot a^2}{4} = dfrac{sqrt{3} cdot 12^2}{4} = dfrac{sqrt{3} cdot 144}{4} = 36 sqrt{3} : см^2 approx 62.35383 : см^2
Ответ: 36 sqrt{3} : см^2 approx 62.35383 : см^2
Проверка .
Площадь треугольника — все формулы, калькулятор онлайн
Площадь треугольника — это численная характеристика, показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц. В зависимости от типа треугольника и известных исходных данных, площадь треугольника можно рассчитать по различным формулам. Приведенные калькуляторы площади треугольника используют все известные методики и упрощают процесс вычислений.
Треугольник — это геометрическая фигура, образованная соединением отрезков трех точек, не лежащих на одной прямой. Точки называются вершинами треугольника, а отрезки — его сторонами.
Площадь треугольника — калькуляторы для всех видов
Треугольники бывают остроугольными, тупоугольными, прямоугольными, разносторонними, равносторонними, равнобедренными. Рассмотренные в данном пункте калькуляторы и формулы подходят для всех видов треугольников.
Зная сторону треугольника (основание) и высоту проведенную к основанию, можно найти его площадь. Площадь треугольника будет равна половине произведения основания на высоту. Основанием треугольника может быть выбрана любая из сторон треугольника.
Площадь треугольника по основанию и высоте — калькулятор онлайн:
| Формула | Результат |
| S = ½ × a × h | |
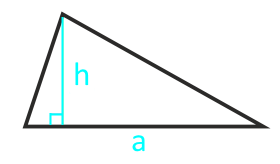 |
Сторона a |
|
Высота h |
Если известно две стороны треугольника и угол между ними, то площадь данного треугольника вычисляется, как половина произведения этих сторон умноженная на синус угла между ними. Угол α между сторонами может быть любым: тупым, острым, прямым.
Площадь треугольника по двум сторонам и углу между ними — расчет:
| Формула | Результат |
| S = ½ × a × b × α | |
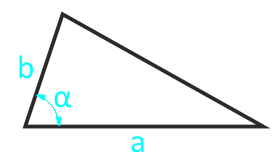 |
Сторона a |
|
Сторона b |
|
|
Угол α° между сторонами a и b |
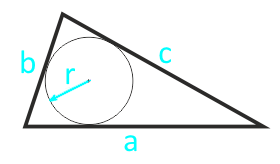
Если известно три стороны треугольника и радиус вписанной окружности, то площадь данного треугольника вычисляется, как половина суммы этих сторон (полупериметр p = ½ × (a + b + c)) умноженная на радиус вписанной окружности.
Площадь треугольника по радиусу вписанной окружности и трем сторонам — онлайн калькулятор:
| Формула | Результат |
| S = r × ½ × (a + b + c) | |
 |
Сторона a |
|
Сторона b |
|
|
Сторона c |
|
|
Радиус r вписанной окружности |
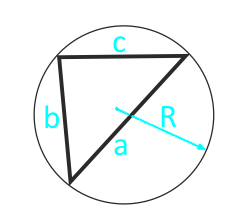
Если известно три стороны треугольника и радиус описанной окружности, то площадь треугольника равна частному от деления произведения сторон треугольника на четыре радиуса описанной около треугольника окружности.
Площадь треугольника по радиусу описанной окружности и трем сторонам — расчет:
| Формула | Результат |
| S = (a × b × c) ⁄ (4 × R) | |
 |
Сторона a |
|
Сторона b |
|
|
Сторона c |
|
|
Радиус R описанной окружности |
Площадь треугольника по формуле Герона равна корню из произведения разностей полупериметра треугольника (p) и каждой из его сторон (a, b, c) на полупериметр. Полупериметр p = (a + b + c) × ½.
Площадь треугольника по формуле Герона — калькулятор онлайн:
| Формула | Результат |
| S = √ p × (p — a) × (p — b) × (p — c) | |
 |
Сторона a |
|
Сторона b |
|
|
Сторона c |
Площадь произвольного треугольника по стороне и двум прилежащим углам — расчет:
| Формула | Результат |
| S = ½ × a² × (sin α × sin β) ⁄ sin (180 — (α + β)) | |
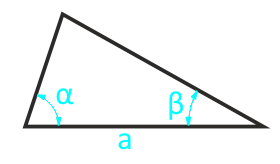 |
Сторона a |
|
Угол β° |
|
|
Угол α° |
Калькулятор площади для равнобедренных треугольников
Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по длине. Боковыми называются равные стороны, а последняя неравная им сторона — основанием. Угол, образованный боковыми сторонами, называется вершинным углом, а углы, одной из сторон которых является основание, называются углами при основании.
Площадь равнобедренного треугольника по боковым сторонам и основанию — калькулятор:
| Формула | Результат |
| S = ¼ × c × √ (4 × a² — c²) | |
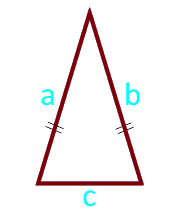 |
Сторона a (a = b) |
|
Сторона c |
Если известны боковые стороны и угол между ними, то площадь равнобедренного треугольника определяется, как половина произведения квадрата боковой стороны на синус угла между боковыми сторонами.
Площадь равнобедренного треугольника по боковым сторонам и углу между ними:
| Формула | Результат |
| S = ½ × a² × sin (α) | |
 |
Боковая сторона a (a = b) |
|
Угол α° между боковыми сторонами |
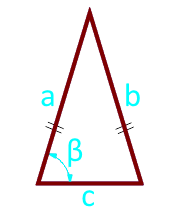
Если известна боковая сторона, основание и углу между ними, то площадь равнобедренного треугольника равна половине произведения боковой стороны и основания на синус угла между ними.
Площадь равнобедренного треугольника по боковой стороне, основанию и углу между ними — расчет:
| Формула | Результат |
| S = ½ ×a × c × sin (β) | |
 |
Боковая сторона a (a = b) |
|
Основание треугольника c |
|
|
Угол β° между основанием и стороной |
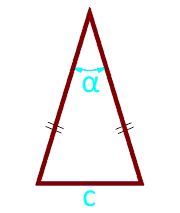
Если известно основание и угол между боковыми сторонами, то площадь равнобедренного треугольника рассчитывается, как четверть отношения квадрата основания на тангенс половинного угла между боковыми сторонами.
Площадь равнобедренного треугольника по основанию и углу между боковыми сторонами — онлайн:
| Формула | Результат |
| S = c² ⁄ (4 × tg (½ × α)) | |
 |
Основание треугольника c |
|
Угол α° между боковыми сторонами |
Площадь равнобедренного треугольника по высоте и основанию — калькулятор:
| Формула | Результат |
| S = ½ × c × h | |
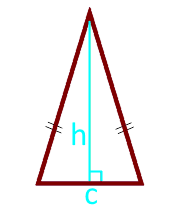 |
Основание треугольника c |
|
Высота h |
Площадь равносторонних треугольников — онлайн калькулятор, формулы
Правильный (равносторонний, или равноугольный) треугольник — это правильный многоугольник, все стороны которого равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.
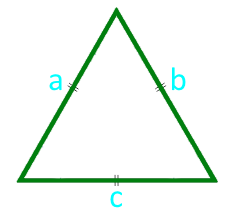
Площадь равностороннего треугольника по известной стороне равна произведению одной четвертой корня из трех на квадрат стороны.
Площадь равностороннего треугольника по стороне — онлайн расчет:
| Формула | Результат |
| S = ¼ × √(3) × a² | |
 |
Сторона a (a = b = c) |
Если известна высота равностороннего треугольника, то его площадь равна отношению квадрата высоты к корню из трех.
Площадь равностороннего треугольника по высоте:
| Формула | Результат |
| S = h² ⁄ √(3) | |
 |
Высота h |
Если известен радиус вписанной окружности, то площадь равностороннего треугольника равна произведению трех корней из трех на квадрат радиуса вписанной окружности.
Площадь равностороннего треугольника по радиусу вписанной окружности — калькулятор:
| Формула | Результат |
| S = 3 × √(3) × r² | |
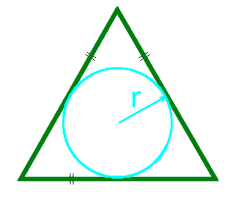 |
Радиус r вписанной окружности |
По известному радиусу описанной окружности площадь равностороннего треугольника определяется, как произведение трех четвертей корня из трех на квадрат радиуса.
Площадь равностороннего треугольника по радиусу описанной окружности:
| Формула | Результат |
| S = ¾ × √(3) × R² | |
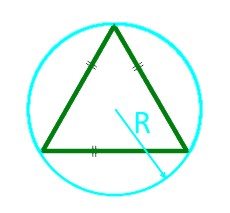 |
Радиус R описанной окружности |
Площадь прямоугольного треугольника — формулы и калькуляторы
Прямоугольный треугольник — это треугольник, в котором один угол прямой (90°).
По основанию и высоте площадь прямоугольно треугольника равна половине произведения катетов треугольника.
Площадь прямоугольного треугольника по двум катетам — расчет:
| Формула | Результат |
| S = ½ × a × b | |
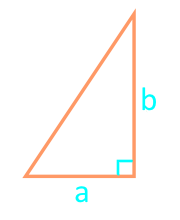 |
Катет a |
|
Катет b |
Площадь прямоугольного треугольника через гипотенузу и угол:
| Формула | Результат |
| S = ¼ × c² × sin (2α) | |
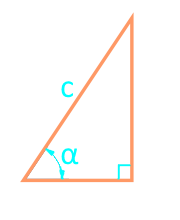 |
Сторона c |
|
Угол α |
Площадь прямоугольного треугольника через катет и угол — онлайн калькулятор:
| Формула | Результат |
| S = ½ × b² × tg (α) | |
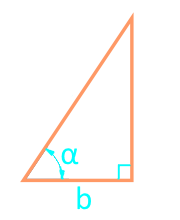 |
Сторона b |
|
Угол α |
Если в треугольник вписана окружность и известны отрезки, на которые она делит гипотенузу, то площадь прямоугольно треугольника равна произведению этих отрезков.
Площадь прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность:
| Формула | Результат |
| S = d × e | |
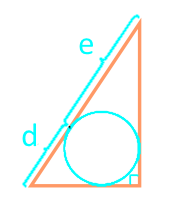 |
Отрезок d |
|
Отрезок e |
Площадь прямоугольного треугольника через гипотенузу и вписанную окружность — расчет:
| Формула | Результат |
| S = r × (r + c) | |
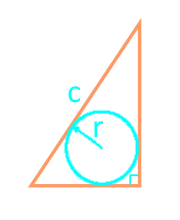 |
Сторона с |
|
Радиус r |
Площадь прямоугольно треугольника по трем сторонам (формула Герона) равна произведению разностей полупериметра треугольника и каждого из катетов. Полупериметр p = ½ × (a + b + c)
Площадь прямоугольного треугольника по формуле Герона:
| Формула | Результат |
| S = ( ½ × (a + b + c) — a) × ( ½ × (a + b + c) — b) | |
 |
Сторона a |
|
Сторона b |
|
|
Сторона c |
Таблица синусов (sin) для расчета площади треугольника
Таблица синусов — это записанные в таблицу посчитанные значения синусов углов от 0° до 360°. Используя ее вы сможете провести расчеты площади треугольника самостоятельно при помощи формул.
Таблица подходит для вычисления:
- Площади прямоугольного треугольника через гипотенузу и угол S = ¼ × c² × sin (2α).
- Площади равнобедренного треугольника по боковой стороне, основанию и углу между ними S = ½ ×a × c × sin (β).
- Площади равнобедренного треугольника по боковым сторонам и углу между ними S = ½ × a² × sin (α).
- Площади произвольного треугольника по стороне и двум прилежащим углам S = ½ × a² × (sin α × sin β) ⁄ sin (180 — (α + β)).
Таблица синусов (sin) углов от 0° до 180°:
| sin(0°) = 0 sin(1°) = 0.017452 sin(2°) = 0.034899 sin(3°) = 0.052336 sin(4°) = 0.069756 sin(5°) = 0.087156 sin(6°) = 0.104528 sin(7°) = 0.121869 sin(8°) = 0.139173 sin(9°) = 0.156434 sin(10°) = 0.173648 sin(11°) = 0.190809 sin(12°) = 0.207912 sin(13°) = 0.224951 sin(14°) = 0.241922 sin(15°) = 0.258819 sin(16°) = 0.275637 sin(17°) = 0.292372 sin(18°) = 0.309017 sin(19°) = 0.325568 sin(20°) = 0.34202 sin(21°) = 0.358368 sin(22°) = 0.374607 sin(23°) = 0.390731 sin(24°) = 0.406737 sin(25°) = 0.422618 sin(26°) = 0.438371 sin(27°) = 0.45399 sin(28°) = 0.469472 sin(29°) = 0.48481 sin(30°) = 0.5 sin(31°) = 0.515038 sin(32°) = 0.529919 sin(33°) = 0.544639 sin(34°) = 0.559193 sin(35°) = 0.573576 sin(36°) = 0.587785 sin(37°) = 0.601815 sin(38°) = 0.615661 sin(39°) = 0.62932 sin(40°) = 0.642788 sin(41°) = 0.656059 sin(42°) = 0.669131 sin(43°) = 0.681998 sin(44°) = 0.694658 sin(45°) = 0.707107 |
sin(46°) = 0.71934 sin(47°) = 0.731354 sin(48°) = 0.743145 sin(49°) = 0.75471 sin(50°) = 0.766044 sin(51°) = 0.777146 sin(52°) = 0.788011 sin(53°) = 0.798636 sin(54°) = 0.809017 sin(55°) = 0.819152 sin(56°) = 0.829038 sin(57°) = 0.838671 sin(58°) = 0.848048 sin(59°) = 0.857167 sin(60°) = 0.866025 sin(61°) = 0.87462 sin(62°) = 0.882948 sin(63°) = 0.891007 sin(64°) = 0.898794 sin(65°) = 0.906308 sin(66°) = 0.913545 sin(67°) = 0.920505 sin(68°) = 0.927184 sin(69°) = 0.93358 sin(70°) = 0.939693 sin(71°) = 0.945519 sin(72°) = 0.951057 sin(73°) = 0.956305 sin(74°) = 0.961262 sin(75°) = 0.965926 sin(76°) = 0.970296 sin(77°) = 0.97437 sin(78°) = 0.978148 sin(79°) = 0.981627 sin(80°) = 0.984808 sin(81°) = 0.987688 sin(82°) = 0.990268 sin(83°) = 0.992546 sin(84°) = 0.994522 sin(85°) = 0.996195 sin(86°) = 0.997564 sin(87°) = 0.99863 sin(88°) = 0.999391 sin(89°) = 0.999848 sin(90°) = 1 |
sin(91°) = 0.999848 sin(92°) = 0.999391 sin(93°) = 0.99863 sin(94°) = 0.997564 sin(95°) = 0.996195 sin(96°) = 0.994522 sin(97°) = 0.992546 sin(98°) = 0.990268 sin(99°) = 0.987688 sin(100°) = 0.984808 sin(101°) = 0.981627 sin(102°) = 0.978148 sin(103°) = 0.97437 sin(104°) = 0.970296 sin(105°) = 0.965926 sin(106°) = 0.961262 sin(107°) = 0.956305 sin(108°) = 0.951057 sin(109°) = 0.945519 sin(110°) = 0.939693 sin(111°) = 0.93358 sin(112°) = 0.927184 sin(113°) = 0.920505 sin(114°) = 0.913545 sin(115°) = 0.906308 sin(116°) = 0.898794 sin(117°) = 0.891007 sin(118°) = 0.882948 sin(119°) = 0.87462 sin(120°) = 0.866025 sin(121°) = 0.857167 sin(122°) = 0.848048 sin(123°) = 0.838671 sin(124°) = 0.829038 sin(125°) = 0.819152 sin(126°) = 0.809017 sin(127°) = 0.798636 sin(128°) = 0.788011 sin(129°) = 0.777146 sin(130°) = 0.766044 sin(131°) = 0.75471 sin(132°) = 0.743145 sin(133°) = 0.731354 sin(134°) = 0.71934 sin(135°) = 0.707107 |
sin(136°) = 0.694658 sin(137°) = 0.681998 sin(138°) = 0.669131 sin(139°) = 0.656059 sin(140°) = 0.642788 sin(141°) = 0.62932 sin(142°) = 0.615661 sin(143°) = 0.601815 sin(144°) = 0.587785 sin(145°) = 0.573576 sin(146°) = 0.559193 sin(147°) = 0.544639 sin(148°) = 0.529919 sin(149°) = 0.515038 sin(150°) = 0.5 sin(151°) = 0.48481 sin(152°) = 0.469472 sin(153°) = 0.45399 sin(154°) = 0.438371 sin(155°) = 0.422618 sin(156°) = 0.406737 sin(157°) = 0.390731 sin(158°) = 0.374607 sin(159°) = 0.358368 sin(160°) = 0.34202 sin(161°) = 0.325568 sin(162°) = 0.309017 sin(163°) = 0.292372 sin(164°) = 0.275637 sin(165°) = 0.258819 sin(166°) = 0.241922 sin(167°) = 0.224951 sin(168°) = 0.207912 sin(169°) = 0.190809 sin(170°) = 0.173648 sin(171°) = 0.156434 sin(172°) = 0.139173 sin(173°) = 0.121869 sin(174°) = 0.104528 sin(175°) = 0.087156 sin(176°) = 0.069756 sin(177°) = 0.052336 sin(178°) = 0.034899 sin(179°) = 0.017452 sin(180°) = 0 |
Таблица синусов (sin) углов от 181° до 360°:
| sin(181°) = -0.017452 sin(182°) = -0.034899 sin(183°) = -0.052336 sin(184°) = -0.069756 sin(185°) = -0.087156 sin(186°) = -0.104528 sin(187°) = -0.121869 sin(188°) = -0.139173 sin(189°) = -0.156434 sin(190°) = -0.173648 sin(191°) = -0.190809 sin(192°) = -0.207912 sin(193°) = -0.224951 sin(194°) = -0.241922 sin(195°) = -0.258819 sin(196°) = -0.275637 sin(197°) = -0.292372 sin(198°) = -0.309017 sin(199°) = -0.325568 sin(200°) = -0.34202 sin(201°) = -0.358368 sin(202°) = -0.374607 sin(203°) = -0.390731 sin(204°) = -0.406737 sin(205°) = -0.422618 sin(206°) = -0.438371 sin(207°) = -0.45399 sin(208°) = -0.469472 sin(209°) = -0.48481 sin(210°) = -0.5 sin(211°) = -0.515038 sin(212°) = -0.529919 sin(213°) = -0.544639 sin(214°) = -0.559193 sin(215°) = -0.573576 sin(216°) = -0.587785 sin(217°) = -0.601815 sin(218°) = -0.615661 sin(219°) = -0.62932 sin(220°) = -0.642788 sin(221°) = -0.656059 sin(222°) = -0.669131 sin(223°) = -0.681998 sin(224°) = -0.694658 sin(225°) = -0.707107 |
sin(226°) = -0.71934 sin(227°) = -0.731354 sin(228°) = -0.743145 sin(229°) = -0.75471 sin(230°) = -0.766044 sin(231°) = -0.777146 sin(232°) = -0.788011 sin(233°) = -0.798636 sin(234°) = -0.809017 sin(235°) = -0.819152 sin(236°) = -0.829038 sin(237°) = -0.838671 sin(238°) = -0.848048 sin(239°) = -0.857167 sin(240°) = -0.866025 sin(241°) = -0.87462 sin(242°) = -0.882948 sin(243°) = -0.891007 sin(244°) = -0.898794 sin(245°) = -0.906308 sin(246°) = -0.913545 sin(247°) = -0.920505 sin(248°) = -0.927184 sin(249°) = -0.93358 sin(250°) = -0.939693 sin(251°) = -0.945519 sin(252°) = -0.951057 sin(253°) = -0.956305 sin(254°) = -0.961262 sin(255°) = -0.965926 sin(256°) = -0.970296 sin(257°) = -0.97437 sin(258°) = -0.978148 sin(259°) = -0.981627 sin(260°) = -0.984808 sin(261°) = -0.987688 sin(262°) = -0.990268 sin(263°) = -0.992546 sin(264°) = -0.994522 sin(265°) = -0.996195 sin(266°) = -0.997564 sin(267°) = -0.99863 sin(268°) = -0.999391 sin(269°) = -0.999848 sin(270°) = -1 |
sin(271°) = -0.999848 sin(272°) = -0.999391 sin(273°) = -0.99863 sin(274°) = -0.997564 sin(275°) = -0.996195 sin(276°) = -0.994522 sin(277°) = -0.992546 sin(278°) = -0.990268 sin(279°) = -0.987688 sin(280°) = -0.984808 sin(281°) = -0.981627 sin(282°) = -0.978148 sin(283°) = -0.97437 sin(284°) = -0.970296 sin(285°) = -0.965926 sin(286°) = -0.961262 sin(287°) = -0.956305 sin(288°) = -0.951057 sin(289°) = -0.945519 sin(290°) = -0.939693 sin(291°) = -0.93358 sin(292°) = -0.927184 sin(293°) = -0.920505 sin(294°) = -0.913545 sin(295°) = -0.906308 sin(296°) = -0.898794 sin(297°) = -0.891007 sin(298°) = -0.882948 sin(299°) = -0.87462 sin(300°) = -0.866025 sin(301°) = -0.857167 sin(302°) = -0.848048 sin(303°) = -0.838671 sin(304°) = -0.829038 sin(305°) = -0.819152 sin(306°) = -0.809017 sin(307°) = -0.798636 sin(308°) = -0.788011 sin(309°) = -0.777146 sin(310°) = -0.766044 sin(311°) = -0.75471 sin(312°) = -0.743145 sin(313°) = -0.731354 sin(314°) = -0.71934 sin(315°) = -0.707107 |
sin(316°) = -0.694658 sin(317°) = -0.681998 sin(318°) = -0.669131 sin(319°) = -0.656059 sin(320°) = -0.642788 sin(321°) = -0.62932 sin(322°) = -0.615661 sin(323°) = -0.601815 sin(324°) = -0.587785 sin(325°) = -0.573576 sin(326°) = -0.559193 sin(327°) = -0.544639 sin(328°) = -0.529919 sin(329°) = -0.515038 sin(330°) = -0.5 sin(331°) = -0.48481 sin(332°) = -0.469472 sin(333°) = -0.45399 sin(334°) = -0.438371 sin(335°) = -0.422618 sin(336°) = -0.406737 sin(337°) = -0.390731 sin(338°) = -0.374607 sin(339°) = -0.358368 sin(340°) = -0.34202 sin(341°) = -0.325568 sin(342°) = -0.309017 sin(343°) = -0.292372 sin(344°) = -0.275637 sin(345°) = -0.258819 sin(346°) = -0.241922 sin(347°) = -0.224951 sin(348°) = -0.207912 sin(349°) = -0.190809 sin(350°) = -0.173648 sin(351°) = -0.156434 sin(352°) = -0.139173 sin(353°) = -0.121869 sin(354°) = -0.104528 sin(355°) = -0.087156 sin(356°) = -0.069756 sin(357°) = -0.052336 sin(358°) = -0.034899 sin(359°) = -0.017452 sin(360°) = 0 |
Таблица тангенсов (tg) для расчета площади треугольника
Таблица тангенсов — это записанные в таблицу посчитанные значения тангенсов углов от 0° до 360°. С ее помощью вы сможете провести расчеты площади треугольника самостоятельно по следующим формулам:
- S = ½ × b² × tg (α) — площадь прямоугольного треугольника через катет и угол.
- S = c² ⁄ (4 × tg (½ × α)) — площадь равнобедренного треугольника по основанию и углу между боковыми сторонами.
Таблица тангенсов (tg) углов от 0° до 180°:
| tg(0°) = 0 tg(1°) = 0.01746 tg(2°) = 0.03492 tg(3°) = 0.05241 tg(4°) = 0.06993 tg(5°) = 0.08749 tg(6°) = 0.1051 tg(7°) = 0.12278 tg(8°) = 0.14054 tg(9°) = 0.15838 tg(10°) = 0.17633 tg(11°) = 0.19438 tg(12°) = 0.21256 tg(13°) = 0.23087 tg(14°) = 0.24933 tg(15°) = 0.26795 tg(16°) = 0.28675 tg(17°) = 0.30573 tg(18°) = 0.32492 tg(19°) = 0.34433 tg(20°) = 0.36397 tg(21°) = 0.38386 tg(22°) = 0.40403 tg(23°) = 0.42447 tg(24°) = 0.44523 tg(25°) = 0.46631 tg(26°) = 0.48773 tg(27°) = 0.50953 tg(28°) = 0.53171 tg(29°) = 0.55431 tg(30°) = 0.57735 tg(31°) = 0.60086 tg(32°) = 0.62487 tg(33°) = 0.64941 tg(34°) = 0.67451 tg(35°) = 0.70021 tg(36°) = 0.72654 tg(37°) = 0.75355 tg(38°) = 0.78129 tg(39°) = 0.80978 tg(40°) = 0.8391 tg(41°) = 0.86929 tg(42°) = 0.9004 tg(43°) = 0.93252 tg(44°) = 0.96569 tg(45°) = 1 tg(46°) = 1.03553 tg(47°) = 1.07237 tg(48°) = 1.11061 tg(49°) = 1.15037 tg(50°) = 1.19175 tg(51°) = 1.2349 tg(52°) = 1.27994 tg(53°) = 1.32704 tg(54°) = 1.37638 tg(55°) = 1.42815 tg(56°) = 1.48256 tg(57°) = 1.53986 tg(58°) = 1.60033 tg(59°) = 1.66428 tg(60°) = 1.73205 |
tg(61°) = 1.80405 tg(62°) = 1.88073 tg(63°) = 1.96261 tg(64°) = 2.0503 tg(65°) = 2.14451 tg(66°) = 2.24604 tg(67°) = 2.35585 tg(68°) = 2.47509 tg(69°) = 2.60509 tg(70°) = 2.74748 tg(71°) = 2.90421 tg(72°) = 3.07768 tg(73°) = 3.27085 tg(74°) = 3.48741 tg(75°) = 3.73205 tg(76°) = 4.01078 tg(77°) = 4.33148 tg(78°) = 4.70463 tg(79°) = 5.14455 tg(80°) = 5.67128 tg(81°) = 6.31375 tg(82°) = 7.11537 tg(83°) = 8.14435 tg(84°) = 9.51436 tg(85°) = 11.43005 tg(86°) = 14.30067 tg(87°) = 19.08114 tg(88°) = 28.63625 tg(89°) = 57.28996 tg(90°) = ∞ tg(91°) = -57.28996 tg(92°) = -28.63625 tg(93°) = -19.08114 tg(94°) = -14.30067 tg(95°) = -11.43005 tg(96°) = -9.51436 tg(97°) = -8.14435 tg(98°) = -7.11537 tg(99°) = -6.31375 tg(100°) = -5.67128 tg(101°) = -5.14455 tg(102°) = -4.70463 tg(103°) = -4.33148 tg(104°) = -4.01078 tg(105°) = -3.73205 tg(106°) = -3.48741 tg(107°) = -3.27085 tg(108°) = -3.07768 tg(109°) = -2.90421 tg(110°) = -2.74748 tg(111°) = -2.60509 tg(112°) = -2.47509 tg(113°) = -2.35585 tg(114°) = -2.24604 tg(115°) = -2.14451 tg(116°) = -2.0503 tg(117°) = -1.96261 tg(118°) = -1.88073 tg(119°) = -1.80405 tg(120°) = -1.73205 |
tg(121°) = -1.66428 tg(122°) = -1.60033 tg(123°) = -1.53986 tg(124°) = -1.48256 tg(125°) = -1.42815 tg(126°) = -1.37638 tg(127°) = -1.32704 tg(128°) = -1.27994 tg(129°) = -1.2349 tg(130°) = -1.19175 tg(131°) = -1.15037 tg(132°) = -1.11061 tg(133°) = -1.07237 tg(134°) = -1.03553 tg(135°) = -1 tg(136°) = -0.96569 tg(137°) = -0.93252 tg(138°) = -0.9004 tg(139°) = -0.86929 tg(140°) = -0.8391 tg(141°) = -0.80978 tg(142°) = -0.78129 tg(143°) = -0.75355 tg(144°) = -0.72654 tg(145°) = -0.70021 tg(146°) = -0.67451 tg(147°) = -0.64941 tg(148°) = -0.62487 tg(149°) = -0.60086 tg(150°) = -0.57735 tg(151°) = -0.55431 tg(152°) = -0.53171 tg(153°) = -0.50953 tg(154°) = -0.48773 tg(155°) = -0.46631 tg(156°) = -0.44523 tg(157°) = -0.42447 tg(158°) = -0.40403 tg(159°) = -0.38386 tg(160°) = -0.36397 tg(161°) = -0.34433 tg(162°) = -0.32492 tg(163°) = -0.30573 tg(164°) = -0.28675 tg(165°) = -0.26795 tg(166°) = -0.24933 tg(167°) = -0.23087 tg(168°) = -0.21256 tg(169°) = -0.19438 tg(170°) = -0.17633 tg(171°) = -0.15838 tg(172°) = -0.14054 tg(173°) = -0.12278 tg(174°) = -0.1051 tg(175°) = -0.08749 tg(176°) = -0.06993 tg(177°) = -0.05241 tg(178°) = -0.03492 tg(179°) = -0.01746 tg(180°) = 0 |
Таблица тангенсов (tg) углов от 181° до 360°:
| tg(181°) = 0.01746 tg(182°) = 0.03492 tg(183°) = 0.05241 tg(184°) = 0.06993 tg(185°) = 0.08749 tg(186°) = 0.1051 tg(187°) = 0.12278 tg(188°) = 0.14054 tg(189°) = 0.15838 tg(190°) = 0.17633 tg(191°) = 0.19438 tg(192°) = 0.21256 tg(193°) = 0.23087 tg(194°) = 0.24933 tg(195°) = 0.26795 tg(196°) = 0.28675 tg(197°) = 0.30573 tg(198°) = 0.32492 tg(199°) = 0.34433 tg(200°) = 0.36397 tg(201°) = 0.38386 tg(202°) = 0.40403 tg(203°) = 0.42447 tg(204°) = 0.44523 tg(205°) = 0.46631 tg(206°) = 0.48773 tg(207°) = 0.50953 tg(208°) = 0.53171 tg(209°) = 0.55431 tg(210°) = 0.57735 tg(211°) = 0.60086 tg(212°) = 0.62487 tg(213°) = 0.64941 tg(214°) = 0.67451 tg(215°) = 0.70021 tg(216°) = 0.72654 tg(217°) = 0.75355 tg(218°) = 0.78129 tg(219°) = 0.80978 tg(220°) = 0.8391 tg(221°) = 0.86929 tg(222°) = 0.9004 tg(223°) = 0.93252 tg(224°) = 0.96569 tg(225°) = 1 tg(226°) = 1.03553 tg(227°) = 1.07237 tg(228°) = 1.11061 tg(229°) = 1.15037 tg(230°) = 1.19175 tg(231°) = 1.2349 tg(232°) = 1.27994 tg(233°) = 1.32704 tg(234°) = 1.37638 tg(235°) = 1.42815 tg(236°) = 1.48256 tg(237°) = 1.53986 tg(238°) = 1.60033 tg(239°) = 1.66428 tg(240°) = 1.73205 |
tg(241°) = 1.80405 tg(242°) = 1.88073 tg(243°) = 1.96261 tg(244°) = 2.0503 tg(245°) = 2.14451 tg(246°) = 2.24604 tg(247°) = 2.35585 tg(248°) = 2.47509 tg(249°) = 2.60509 tg(250°) = 2.74748 tg(251°) = 2.90421 tg(252°) = 3.07768 tg(253°) = 3.27085 tg(254°) = 3.48741 tg(255°) = 3.73205 tg(256°) = 4.01078 tg(257°) = 4.33148 tg(258°) = 4.70463 tg(259°) = 5.14455 tg(260°) = 5.67128 tg(261°) = 6.31375 tg(262°) = 7.11537 tg(263°) = 8.14435 tg(264°) = 9.51436 tg(265°) = 11.43005 tg(266°) = 14.30067 tg(267°) = 19.08114 tg(268°) = 28.63625 tg(269°) = 57.28996 tg(270°) = ∞ tg(271°) = -57.28996 tg(272°) = -28.63625 tg(273°) = -19.08114 tg(274°) = -14.30067 tg(275°) = -11.43005 tg(276°) = -9.51436 tg(277°) = -8.14435 tg(278°) = -7.11537 tg(279°) = -6.31375 tg(280°) = -5.67128 tg(281°) = -5.14455 tg(282°) = -4.70463 tg(283°) = -4.33148 tg(284°) = -4.01078 tg(285°) = -3.73205 tg(286°) = -3.48741 tg(287°) = -3.27085 tg(288°) = -3.07768 tg(289°) = -2.90421 tg(290°) = -2.74748 tg(291°) = -2.60509 tg(292°) = -2.47509 tg(293°) = -2.35585 tg(294°) = -2.24604 tg(295°) = -2.14451 tg(296°) = -2.0503 tg(297°) = -1.96261 tg(298°) = -1.88073 tg(299°) = -1.80405 tg(300°) = -1.73205 |
tg(301°) = -1.66428 tg(302°) = -1.60033 tg(303°) = -1.53986 tg(304°) = -1.48256 tg(305°) = -1.42815 tg(306°) = -1.37638 tg(307°) = -1.32704 tg(308°) = -1.27994 tg(309°) = -1.2349 tg(310°) = -1.19175 tg(311°) = -1.15037 tg(312°) = -1.11061 tg(313°) = -1.07237 tg(314°) = -1.03553 tg(315°) = -1 tg(316°) = -0.96569 tg(317°) = -0.93252 tg(318°) = -0.9004 tg(319°) = -0.86929 tg(320°) = -0.8391 tg(321°) = -0.80978 tg(322°) = -0.78129 tg(323°) = -0.75355 tg(324°) = -0.72654 tg(325°) = -0.70021 tg(326°) = -0.67451 tg(327°) = -0.64941 tg(328°) = -0.62487 tg(329°) = -0.60086 tg(330°) = -0.57735 tg(331°) = -0.55431 tg(332°) = -0.53171 tg(333°) = -0.50953 tg(334°) = -0.48773 tg(335°) = -0.46631 tg(336°) = -0.44523 tg(337°) = -0.42447 tg(338°) = -0.40403 tg(339°) = -0.38386 tg(340°) = -0.36397 tg(341°) = -0.34433 tg(342°) = -0.32492 tg(343°) = -0.30573 tg(344°) = -0.28675 tg(345°) = -0.26795 tg(346°) = -0.24933 tg(347°) = -0.23087 tg(348°) = -0.21256 tg(349°) = -0.19438 tg(350°) = -0.17633 tg(351°) = -0.15838 tg(352°) = -0.14054 tg(353°) = -0.12278 tg(354°) = -0.1051 tg(355°) = -0.08749 tg(356°) = -0.06993 tg(357°) = -0.05241 tg(358°) = -0.03492 tg(359°) = -0.01746 tg(360°) = 0 |
Площадь треугольника можно посчитать самостоятельно по формулам, или воспользоваться для этого онлайн калькулятором. В рассмотренном материале приведены как формулы и таблицы синусов, тангенсов, так и калькуляторы с возможностью расчета площади 21 способом.