Как найти площадь треугольника если известна диагональ

как найти площадь прямоугольного треугольника

Как найти площадь треугольника, как найти площадь прямоугольного треугольника. Формула нахождения площади треугольника.

Всё о площади треугольника.

1. Формула площади треугольника
2. Пример/задача нахождения площади треугольника
3. Найти площадь треугольника онлайн
4. Найти площадь треугольника если известна сторона и диагональ
5. Найти площадь треугольника онлайн, если известна диагональ и сторона

Формула площади треугольника

Когда мы говорим о формуле площади треугольника, то подразумеваем, что это прямоугольный треугольник(просто… так уж сложилось по умолчанию) :



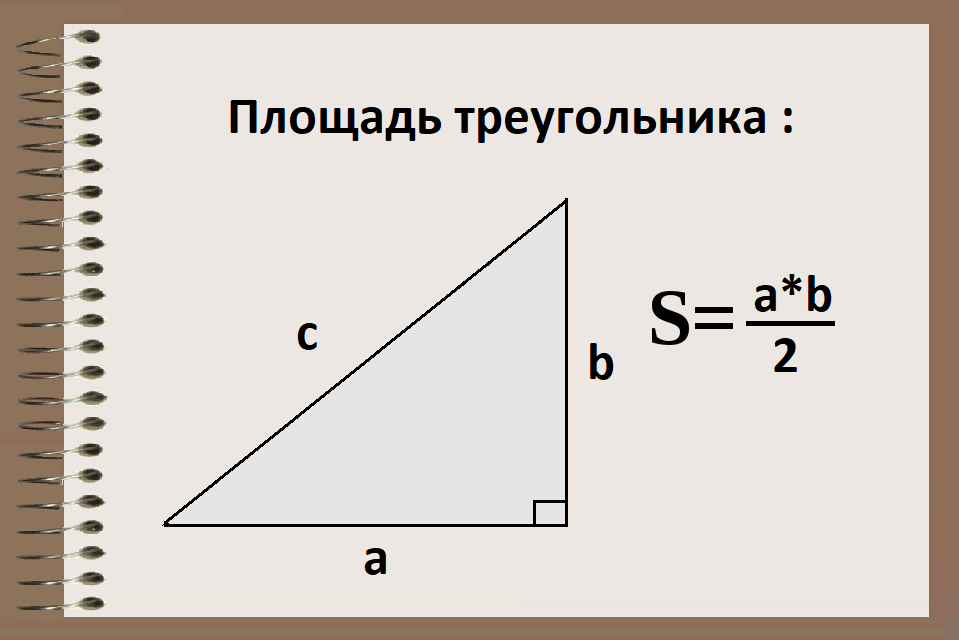
S = a*b/2

Где S – площадь (единица измерения)²

a – длина одной из сторон.

b – длина второй стороны.

Иногда, данная формула не подходит к тому или иному виду треугольников!
Еще смотри – всё о треугольниках

Пример/задача нахождения площади треугольника

Условие задачи :

Требуется найти площадь прямоугольного треугольника. Известно, что один из катетов равен 15см(сторона а). Второй катет равен 8см(сторона b).

Первым шагом, при решении задачи о площади треугольника – требуется узнать вид треугольника, потому. что площадь разных треугольников высчитывается по разному! Здесь мы видим. что в задаче указано, какой подвид треугольника –

прямоугольный

И далее нам нужно взять формулу площади треугольника и подставить в неё все известные параметры.

S =a*b2

a = 15см, и = 8см

S = 15*82 = 1202 = 60см²

Результат данной задачи вы можете проверить в ниже идущем пункте.

Найти площадь треугольника онлайн

Если известно у прямоугольного треугольника сторона “а” и сторона “b”, то для такого треугольника мы можем посчитать площадь онлайн.



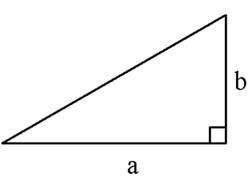
Для того, чтобы посчитать площадь прямоугольного треугольника онлайн, вам требуется в поле :

Первая сторона – заполнить значением первой стороны.

Вторая сторона – заполнить значением второй стороны.

И нажать кнопку посчитать.

Найти площадь треугольника если известна сторона и диагональ

Условие задачи :

Найти площадь прямоугольного треугольника, если диагональ “c” = 10см. Одна сторона равно 8см.


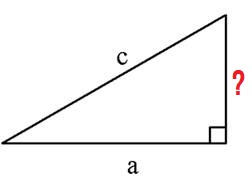
Для нахождения длины неизвестной стороны, нам понадобится “теорема пифагора”. Обозначим неизвестную сторону через “х”

Составляем уравнение : с² = а² +

х

²
Выводим х :

х

=

√

с² – а²
Подставляем данные нашей задачи :

х

=

√

10² – 8² =

√

100 – 64 =

√

36 = 6

После того, как мы нашли недостающую сторону. мы можем найти площадь прямоугольного треугольника по формуле ,

где : b = х
S =a*b2

Подставляем наши данные в формулу:

S = 8 * 62 = 482 = 24см²

Найти площадь треугольника онлайн, если известна диагональ и сторона

Для нахождения неизвестной стороны в прямоугольном треугольнике, написали скрипт, который может посчитать это.



Для того, чтобы найти длину неизвестной стороны и площадь данного прямоугольного треугольника… в поле ввода введите:

В первом поле длину стороны.

Во втором поле введите длину гипотенузы.

Не благодарите, но ссылкой можете поделиться!

COMMENTS+

 
BBcode

---

Как найти площадь треугольника

На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.

Треугольник – это многоугольник с тремя сторонами.

По формуле Герона

Формула Герона для нахождения площади треугольника:

Через основание и высоту

Формула нахождения площади треугольника с помощью половины его основания и высоту:

Через две стороны и угол

Формула нахождения площади треугольника через две стороны и угол между ними:

Через сторону и два прилежащих угла

Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:

Площадь прямоугольного треугольника

Прямоугольный треугольник – треугольник у которого один из углов прямой, т.е. равен 90°.

Формула нахождения площади прямоугольного треугольника через катеты:

Площадь равнобедренного треугольника через стороны

Равнобедренный треугольник – треугольник, в котором две стороны равны. А значит, равны и два угла.

Формула нахождения площади равнобедренного треугольника через две стороны:

Площадь равнобедренного треугольника через основание и угол

Формула нахождения площади равнобедренного треугольника через основание и угол:

Площадь равностороннего треугольника через стороны

Равносторонний треугольник – треугольник, в котором все стороны равны, а каждый угол равен 60°.

Формула нахождения площади равностороннего треугольника через сторону:

Площадь равностороннего треугольника через высоту

Формула нахождения площади равностороннего треугольника через высоту:

Площадь равностороннего треугольника через радиус вписанной окружности

Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:

Площадь равностороннего треугольника через радиус описанной окружности

Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:

Площадь треугольника через радиус описанной окружности и три стороны

Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:

Площадь треугольника через радиус вписанной окружности и три стороны

Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:

как найти площадь прямоугольного треугольника

Как найти площадь треугольника, как найти площадь прямоугольного треугольника. Формула нахождения площади треугольника.

Всё о площади треугольника.

Формула площади треугольника

Когда мы говорим о формуле площади треугольника, то подразумеваем, что это прямоугольный треугольник(просто. так уж сложилось по умолчанию) :

Где S – площадь (единица измерения)²

a – длина одной из сторон.

b – длина второй стороны.

Иногда, данная формула не подходит к тому или иному виду треугольников!

Пример/задача нахождения площади треугольника

Требуется найти площадь прямоугольного треугольника. Известно, что один из катетов равен 15см(сторона а). Второй катет равен 8см(сторона b).

Первым шагом, при решении задачи о площади треугольника – требуется узнать вид треугольника, потому. что площадь разных треугольников высчитывается по разному! Здесь мы видим. что в задаче указано, какой подвид треугольника – прямоугольный

И далее нам нужно взять формулу площади треугольника и подставить в неё все известные параметры.

S = 15*8 2 = 120 2 = 60см²

Результат данной задачи вы можете проверить в ниже идущем пункте.

Найти площадь треугольника онлайн

Если известно у прямоугольного треугольника сторона “а” и сторона “b”, то для такого треугольника мы можем посчитать площадь онлайн.

Для того, чтобы посчитать площадь прямоугольного треугольника онлайн, вам требуется в поле :

Первая сторона – заполнить значением первой стороны.

Вторая сторона – заполнить значением второй стороны.

И нажать кнопку посчитать.

Найти площадь треугольника если известна сторона и диагональ

Найти площадь прямоугольного треугольника, если диагональ “c” = 10см. Одна сторона равно 8см.

Для нахождения длины неизвестной стороны, нам понадобится “теорема пифагора”. Обозначим неизвестную сторону через ” х “

Составляем уравнение : с² = а² + х ²

Выводим х : х = √ с² – а²

Подставляем данные нашей задачи : х = √ 10² – 8² =
√ 100 – 64 = √ 36 = 6

После того, как мы нашли недостающую сторону. мы можем найти площадь прямоугольного треугольника по формуле ,

Подставляем наши данные в формулу:

S = 8 * 6 2 = 48 2 = 24см²

Найти площадь треугольника онлайн , если известна диагональ и сторона

Для нахождения неизвестной стороны в прямоугольном треугольнике, написали скрипт, который может посчитать это.

Для того, чтобы найти длину неизвестной стороны и площадь данного прямоугольного треугольника. в поле ввода введите:

Как найти площадь треугольника – все способы от самых простых до самых сложных

Зависит от того, какой треугольник.

Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.

Если треугольник прямоугольный

То есть один из его углов равен 90 градусам.

Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.

Если он равнобедренный

То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.

Если он равносторонний

То есть все три стороны равны. Ваши действия такие:

1. Найдите квадрат стороны – умножьте эту сторону на нее же. Если у вас сторона равна 4, умножьте 4 на 4, будет 16.
2. Умножьте полученное значение на корень из 3. Это примерно 1,732050807568877293527.
3. Поделите все на 4.

Если известна сторона и высота

Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.

Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.

Если известны две стороны и градус угла между ними

Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:

Если известны длины трех сторон

1. Найдите периметр. Для этого сложите все три стороны.
2. Найдите полупериметр – разделите периметр на два. Запомните значение.
3. Отнимите от полупериметра длину первой стороны. Запомните.
4. Отнимите от полупериметра длину второй стороны. Тоже запомните.
5. Отнимите от полупериметра длину третьей стороны. И ее запомните.
6. Умножьте полупериметр на каждое из этих чисел (разницу с первой, второй и третьей стороной).
7. Найдите квадратный корень.

Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.

Если известны три стороны и радиус описанной окружности

Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.

Если известны три стороны и радиус вписанной окружности

Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.

Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.

Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.

[spoiler title=”источники:”]

http://calc.dwweb.ru/0106_nayti_ploschad_treugolnika.html

http://vsvoemdome.ru/obrazovanie/kak-nayti-ploschad-treugolnika

[/spoiler]

Что такое треугольник

Это весьма узнаваемая, классическая фигура в геометрии, известная даже детишкам дошкольного возраста. Треугольник фактически состоит из трёх точек на плоскости и трёх соединяющих их отрезков. Что важно — точки не могут лежать на одной прямой линии и именуются они вершинами данной фигуры.

Соединяющие отрезки — это стороны, а пространство между ними — внутренность треугольника, площадь которой мы и собираемся вычислить. В зависимости от значений или соотношений сторон и углов выделяют равносторонние, равнобедренные, прямоугольные и др.

Площадь прямоугольного треугольника

Частным будет случай, когда один из углов фигуры равен 90°, то есть является прямым. Двух прямых углов в треугольнике быть просто физически не может, иначе третий будет равен 0°, что невозможно: сумма углов всегда 180° — это закон.

Формула нахождения площади в этом случае чрезвычайно проста: перемножаем катеты и делим результат на два. По сути своей — это половина прямоугольника, что можно сложить из двух таких фигур. Наш онлайн-калькулятор моментально выполнит расчёт.

Важно: если ваши единицы измерения — миллиметры, тогда площадь будет выражаться в мм²; если сантиметры — тогда в см² и так далее …

Площадь треугольника через сторону и прилежащие углы

Чтобы воспользоваться приведённой здесь формулой, необходимо знать длину одной из сторон треугольника и прилежащие к ней углы. На самом деле потребуются значения всех углов, но при наличии двух из них — найти третье не составит труда: сумма углов треугольника всегда равна 180°.

Известное нам значение длины возводится в квадрат, делится на 2 и умножается на следующую дробь: в числителе перемножены синусы прилежащих углов, в знаменателе — синус оставшегося третьего угла.

Важно: если ваши единицы измерения — миллиметры, тогда площадь будет выражаться в мм²; если сантиметры — тогда в см² и так далее …

Площадь треугольника через две стороны и угол

Представленная формула позволит найти площадь любого произвольного треугольника, если мы имеем на руках значения двух его сторон и угла между ними. Для этого необходимо произведение этих сторон умножить на синус угла, и разделить итоговое значение на 2.

Сложно представить, при каких жизненных ситуациях нам может потребоваться производить подобные вычисления, тем не менее у школьников и людей специализированных профессий такая потребность возникает с завидной регулярностью. Для них и создан наш онлайн-калькулятор.

Важно: если ваши единицы измерения — миллиметры, тогда площадь будет выражаться в мм²; если сантиметры — тогда в см² и так далее …

Площадь треугольника по формуле Герона

Герон — греческий математик, изобретатель и механик, живший в первом веке нашей эры. По его формуле площадь треугольника рассчитывается, как корень из произведения разностей полупериметра (p) и каждой из его сторон (a, b, c). Всё, что необходимо знать — значения длин всех сторон.

Формула Герона присутствует в так называемой «Метрике» Герона Александрийского (I век н. э.). Была названа конечно же его именем, хотя говорят её вывел ещё сам Архимед.

Наш онлайн-калькулятор всего за несколько секунд поможет вам найти площадь, достаточно ввести значения длин всех сторон.

Важно: если ваши единицы измерения — миллиметры, тогда площадь будет выражаться в мм²; если сантиметры — тогда в см² и так далее …

Площадь треугольника через основание и высоту

Наш онлайн-калькулятор моментально вычислит для вас площадь треугольника. Существует множество научных способов как её найти.

В данном случае потребуются следующие данные: длина основания (мы обозначили её буквой «b») и опущенная к нему высота (обычно обозначается как «h»). Для вашего удобства мы добавили подробный чертёж с обозначениями.

Важно: если ваши единицы измерения — миллиметры, тогда площадь будет выражаться в мм²; если сантиметры — тогда в см² и так далее …

Ваша оценка?

[Оценок: 11 / Средняя: 4.8]