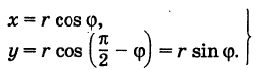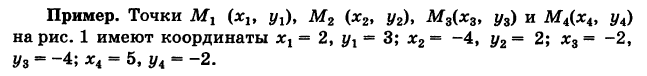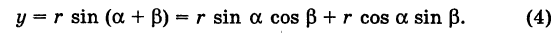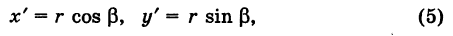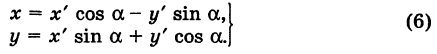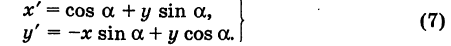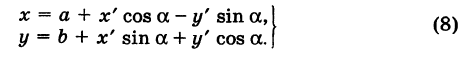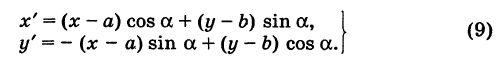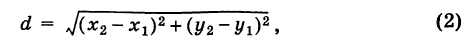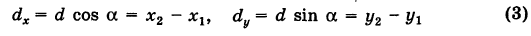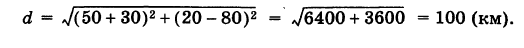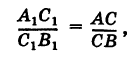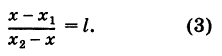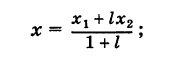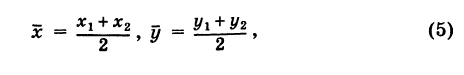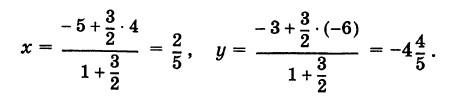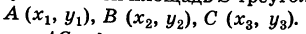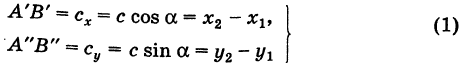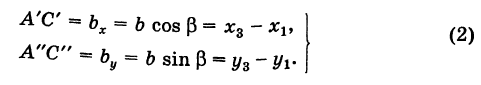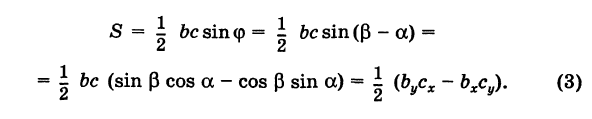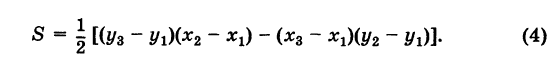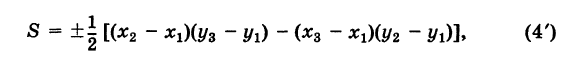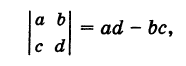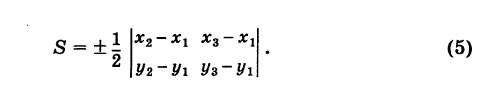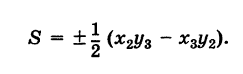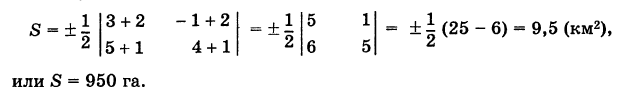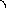Как найти площадь треугольника если известны вершины

Как найти площадь треугольника по координатам его вершин?

1способ:

Найти длины трёх сторон треугольника и вычислить площадь по формуле Герона. Способ удобен, если длины сторон являются целыми числами. В противном случае предстоят громоздкие вычисления.

2 способ:

вывести формулу для нахождения площади и использовать её для вычисления.

Утверждение

Площадь треугольника ABC с вершинами в точках A(x₁;y₁), B(x₂;y₂), C(x₃;y₃) можно вычислить с помощью формулы

   

Доказательство:

Рассмотрим треугольник ABC,

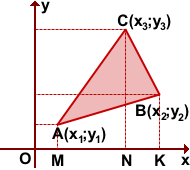
A(x₁;y₁), B(x₂;y₂), C(x₃;y₃)

Опустим перпендикуляры из вершин треугольника на координатные оси.

   

   

   

   

   

   

   

   

   

   

   

   

   

С учетом вариантов взаимного расположения точек A, B и C формула для вычисления площади треугольника по координатам его вершин приобретает вид:

   

Что и требовалось доказать.

3 способ:

Найти длины двух сторон и косинус угла между ними и вычислить площадь треугольника через стороны и синус угла между ними.

4 способ:

Найти длину и уравнение одной стороны треугольника и длину высоты, проведённой к этой стороне. Вычислить площадь через сторону и высоту.

Рассмотрим эти способы на конкретном примере.

Найти площадь треугольника, вершины которого имеют координаты A(-1;-3), B(3;4), C(5;-5).

1 способ:

Находим длины сторон треугольника ABC.

   

   

   

   

   

   

Поскольку длины сторон выражены иррациональными числами, вычислять площадь треугольника по формуле Герона — не самый лучший способ.

2 способ:

Подставляем в формулу x₁=-1, y₁=-3, x₂=3, y₂=4, x₃=5, y₃=-5:

   

   

3 способ:

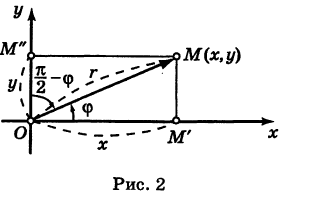
Угол A образован векторами AC и AB. Отсюда

   

Находим координаты векторов:

   

   

   

   

   

   

Скалярное произведение

   

Длины AB и AC уже знаем:

   

   

   

Синус и косинус одного угла связаны соотношением:

   

Синус угла от 0° до 180° является положительным числом, поэтому

   

   

Отсюда

   

   

4 способ:

Найдём уравнение прямой AB. Подставляем координаты A и B в уравнение y=kx+b:

   

Отсюда k=7/4, b=-5/4

   

   

Найдём расстояние от точки C до прямой AB:

   

Это расстояние равно высоте треугольника, проведённой из вершины C к стороне AB. Отсюда

   

Примечание: дробные числа записывайте
через точку, а не запятую.

Округлять до -го знака после запятой.

Прямоугольная система координат на плоскости и ее применение с примерами

Содержание:

Прямоугольная система координат на плоскости и ее применение к простейшим задачам

Прямоугольные координаты точки на плоскости

Координатами точки на плоскости называются числа, определяющие положение этой точки на плоскости.

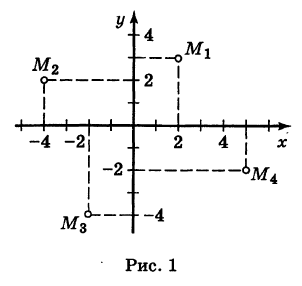
Прямоугольные декартовы координаты (по имени математика Декарта) на плоскости вводятся следующим образом: на этой плоскости выбираются точка О (начало координат) и проходящие через нее взаимно перпендикулярные направленные прямые Ох и Оу (оси координат) (рис. 1). Для удобства рассмотрения будем предполагать, что ось Ох 0ось абсцисс) горизонтальна и направлена слева направо, а ось Оу (ось ординат) вертикальна и направлена снизу вверх; таким образом, ось О у повернута относительно оси Ох на угол 90° против хода часовой стрелки 1 ). Кроме того, выбирается единица масштаба для измерения расстояний.

Для данной точки М введем в рассмотрение два числа: абсциссу х и ординату у этой точки.

Абсциссой х называется число, выражающее в некотором масштабе расстояние от точки до оси ординат, взятое со знаком плюс, если точка лежит вправо от оси ординат, и со знаком минус, если точка лежит влево от оси ординат. Ординатой у называется число, выражающее в некотором масштабе (обыкновенно в том же, как и для абсциссы) расстояние от точки до оси абсцисс, взятое со знаком плюс, если точка лежит выше оси абсцисс, и со знаком минус, если точка лежит ниже оси абсцисс.

Эти два числа х и у и принимаются за координаты точки М, так как они полностью определяют положение точки на плоскости, а именно: каждой паре чисел х и у соответствует единственная точка, координатами которой являются эти числа; и обратно, каждая точка плоскости имеет определенные координаты х и у. Если точка М имеет координаты х и у, то это обстоятельство обозначают так: М (х, у) (на первом месте ставится абсцисса х, а на втором — ордината у). При записи координат знак плюс, как обычно, можно опускать.

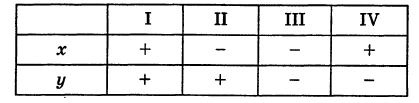
Оси Ох и Оу разбивают плоскость на четыре части, называемые квадрантами. Производя нумерацию квадрантов (I, II, III и IV) в направлении против хода часовой стрелки, отправляясь от того квадранта, где обе координаты положительны, получим следующую таблицу знаков координат:

Отрезок ОМ у соединяющий начало координат О с точкой М (рис. 2), называется ее радиусом-вектором. Обозначая через ф угол, образованный отрезком ОМ с положительным направлением оси Ох, и через 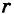его длину, для точки М, лежащей в I квадранте, из треугольников ОММ’ и ОММ” получим

Нетрудно убедиться, что формулы (1) будут справедливы для координат точек всех квадрантов. Таким образом, знак абсциссы х точки М совпадает со знаком косинуса, а знак ее ординаты у — со знаком синуса в соответствующем квадранте.

Легко видеть, что если точка лежит на оси абсцисс, то ее ордината у равна нулю; если же она лежит на оси ординат, ее абсцисса х равна нулю, и обратно. Следовательно, если точка совпадает с началом координат, то равны нулю обе ее координаты.

В дальнейшем прямоугольные декартовы координаты для краткости будем называть просто прямоугольными координатами.

В следующих параграфах рассмотрим некоторые простейшие задачи на применение прямоугольных координат на плоскости.

Преобразование прямоугольной системы координат

При решении задач иногда выгодно вместо данной прямоугольной системы координат выбрать другую прямоугольную систему координат О’х’у определенным образом ориентированную относительно первой. Например, при межпланетных путешествиях можно пользоваться системой координат, связанной с центром Земли (геоцентрическая система координат); однако более удобно использовать систему координат, связанную с центром Солнца (гелиоцентрическая система координат).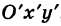

Возникает вопрос о том, как от одной системы координат перейти к другой.

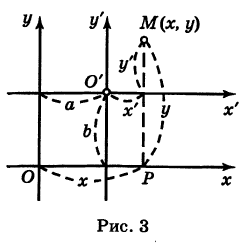
Рассмотрим сначала простейший случай (рис. 3), когда оси «новой системы координат» О’х’у’ параллельны соответствующим осям «старой системы координат о Оху и имеют одинаковые направления с ними (параллельный перенос системы координат).

Пусть начало новой системы координат — точка О’ — имеет координаты (а, Ь) в старой системе координат. Точка М плоскости со «старыми координатами» (х, у) будет иметь некоторые «новые координаты» [х у’] (для ясности мы их обозначаем квадратными скобками). Из рис. 3 непосредственно получаем

х’ = х – а, у’ = у – b, (1)

т. е. новые координаты точки равны ее старым координатам минус старые координаты нового начала.

Обратно, из (1) находим

х = х’ + а, у = у’ + Ь. (2)

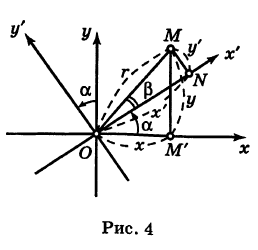
Пусть теперь «новая система» координат Ох’у при неизменном начале О, повернута относительно «старой системы» Оху на угол а (рис. 4), т. е. 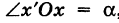, причем а считается положительным, если поворот осуществляется против хода часовой стрелки, и отрицательным — в противоположном случае (поворот системы координат).

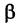
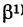
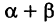
Обозначим через угол, образованный радиусом-вектором г = ОМ точки М с осью Ох’; тогда отрезок ОМ, с учетом знака угла ), будет составлять с осью Ох угол . Отсюда на основании формул (1) из при любом расположении точки М имеем

Так как новые координаты точки М, очевидно, есть

то из формул (3) и (4) получаем

Для запоминания формул (6) используют следующий мнемонический прием: говорят, что первая формула (6) содержит полный беспорядок, а вторая — полный порядок. Действительно, в первой формуле на первом месте стоит cos, на втором — sin; кроме того, присутствует знак минус. Во второй формуле (6) никаких нарушений правильности в этом смысле нет.

Формулы (6) выражают старые координаты х и у точки М через ее новые х’ и у’. Чтобы выразить новые координаты х’ и у’ через старые х и у, достаточно разрешить систему (6) относительно х’и у’. Однако можно поступить проще, а именно принять систему Ох’у’ за «старую», а систему Оху за «новую». Тогда, учитывая, что вторая система повернута относительно первой на угол — а, заменяя в формулах (6) х’ и у’ соответственно на х и у и обратно и принимая во внимание, что cos (-a) = cos a, sin (-a) = -sin a, будем иметь

Наконец, в общем случае, когда новое начало координат есть точка О’ (a, Ь) и ось О’х’ образует с осью Ох угол а, соединяя формулы (2) и (6), находим

Здесь угол Р считается положительным, если радиус-вектор ОМ повернут относительно оси Ох’ против хода часовой стрелки, и отрицательным, если он повернут относительно этой оси по ходу часовой стрелки.

Аналогично, из формул (1) и (7) получаем

Из формул (8) и (9) вытекает, что формулы перехода от одной прямоугольной системы координат к другой прямоугольной системе координат являются линейными функциями как новых, так и старых координат, т. е. содержат эти координаты в первой степени.

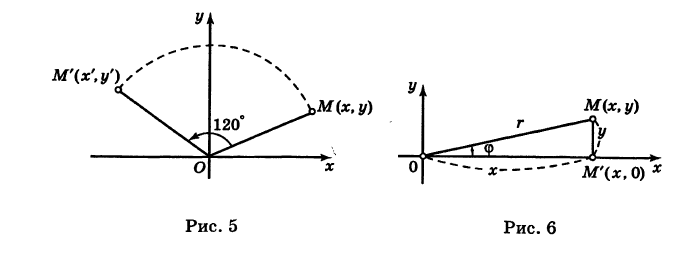
Пример:

Отрезок ОМ, где точка М имеет координаты (х, г/), повернут на угол а = 120° против хода часовой стрелки (рис. 5). Каковы будут координаты х’ и у’ нового положения М’ точки М?

Решение:

Предполагая, что с точкой М связана подвижная система координат Ох’у на основании формул (6) будем иметь

Расстояние между двумя точками на плоскости

1) Найдем сначала расстояние г от начала координат О (0, 0) до точки М (х, у) (рис. 6).

Расстояние г = ОМ, очевидно, является гипотенузой прямоугольного ОММ’ с катетами . По теореме Пифагора получаем

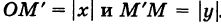
Таким образом, расстояние от начала координат до некоторой точки равно корню квадратному из суммы квадратов координат этой точки.

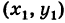
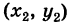
2) В общем случае, пусть для точек A и Б (рис. 7) требуется найти расстояние d = АВ между этими точками.

Выберем новую систему координат Ах’у’ начало которой совпадает с точкой А и оси которой параллельны прежним осям и имеют, соответственно, одинаковые направления с ними. Тогда в новой системе координат точки Л и В будут иметь координаты А [0, 0] и Б 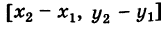. Отсюда на основании формулы (1) получаем

т. е. расстояние между двумя точками плоскости (при любом их расположении) равно корню квадратному из суммы квадратов разностей одноименных координат этих точек.

Замечание. Формула (2) дает также длину отрезка АВ. Легко определить направление этого отрезка. Из прямоугольного А ABC имеем

(dx и dy называются проекциями отрезка АВ на оси координат Оху). Отсюда получаем 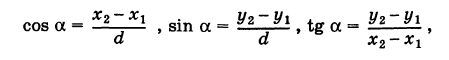где d определяется формулой (2).

Пример:

Танк на местности переместился из точки А (-30, 80) в точку Б (50, 20) (относительно некоторой системы координат Оху)> причем координаты точек даны в километрах. Найти путь d, пройденный танком, если он двигался, не меняя направления.

Решение:

Применяя формулу (2), имеем

Деление отрезка в данном отношении

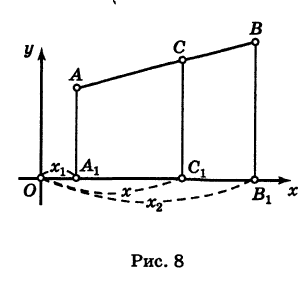
Предположим, что отрезок АВ (рис. 8), соединяющий точки A (xl9 уг) и В (x2t у2), разделен точкой С на два отрезка АС и СБ, причем отношение АС к СБ равно I (I > 0):

Требуется выразить координаты х и у точки С(х, у) через координаты концов отрезка АВ.

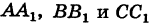
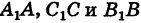
Опустим перпендикуляры соответственно из точек А, В и С на ось Ох. Тогда получим, что три параллельные прямые пересекают стороны угла (не обозначенного на рисунке), образованного прямыми АВ и Ох. Как известно из элементарной геометрии, пучок параллельных прямых рассекает стороны угла на пропорциональные части; поэтому

откуда на основании равенства (1) будем иметь

Из рис. 8 видно, что 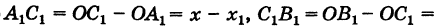х2 – х. Подставляя эти выражения в формулу (2), получим

Решая уравнение (3) относительно неизвестной абсциссы х, будем иметь

Итак, координаты точки С (ху у), делящей отрезок АВ в отношении / (считая от А к В), определяются формулами Если точка С делит отрезок АВ пополам, то АС = СВ и, следовательно, I = АС/СВ = 1. Обозначая координаты середины отрезка АВ через х, у, получим на основании формул (4)

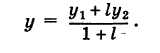
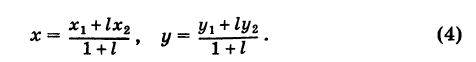
т. е. координаты середины отрезка равны полусуммам соответствующих координат его концов.

Примечание. При выводе формул (4) и (5) мы предполагали, что концы А и В отрезка АВ лежат в первом квадранте и, следовательно, координаты точек Аи В положительны. Легко доказать, что формулы (4) и (5) будут справедливы и в случае произвольного расположения отрезка АВ на координатной плоскости.

Пример:

Вычислить координаты точки С (х, у)> делящей отрезок АВ между точками А (-5, -3) и В (4, -6) в отношении АС/СВ = 3/2.

Решение:

В этом случае I = 3/2 и, следовательно,

Площадь треугольника

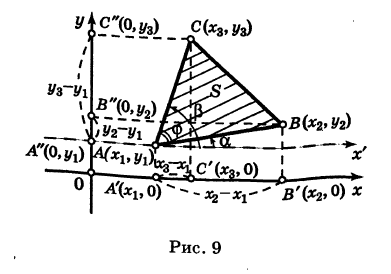
Пусть требуется найти площадь S треугольника ABC (рис. 9) с вершинами

Пусть АВ = с, АС = Ь, а углы, образованные этими сторонами с осью Ох, соответственно равны .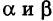

На основании (см. замечание) имеем (рис. 9)

и

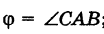
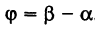
Пусть ; очевидно (рис. 9), . По известной формуле тригонометрии получаем

Отсюда в силу (1) и (2) имеем

Заметим, что формула (4) при ином расположении вершин может дать площадь треугольника S со знаком минус. Поэтому формулу для площади треугольника обычно пишут в виде

где знак выбирается так, чтобы для площади получалось положительное число,

Используя понятие определителя второго порядка

формулу (4′) можно записать в удобной для запоминания форме:

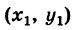
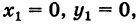
Формула (4′) упрощается, если точка А находится в начале координат. А именно, полагая получим

Отметим, что если точки А, В, С находятся на одной прямой, то площадь S = 0; и обратно, если S = 0, то вершины А, Б и С расположены на одной прямой.

Пример:

Вспаханное поле имеет форму треугольника с вершинами А (-2, -1), В (3, 5) и С (-1, 4) (размеры даны в километрах). Определить площадь S этого поля.

По формуле (5) имеем

Замечание. Вычисление площади многоугольника сводится к вычислению площадей треугольников. Для этого достаточно разбить многоугольник на треугольники, площади которых вычисляют по формуле (4).

Рекомендую подробно изучить предметы:

Математика Алгебра Линейная алгебра Векторная алгебра Высшая математика Дискретная математика Математический анализ Математическая логика

Ещё лекции с примерами решения и объяснением:

• Линии второго порядка
• Полярные координаты
• Непрерывность функции
• Уравнения поверхности и линии в пространстве
• Интегрирование рациональных дробей
• Интегрирование тригонометрических функций
• Интегрирование тригонометрических выражений
• Интегрирование иррациональных функций

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

[spoiler title=”источники:”]

http://mathhelpplanet.com/static.php?p=onlain-reshit-treugolnik

http://www.evkova.org/pryamougolnaya-sistema-koordinat-na-ploskosti

[/spoiler]

Содержание

1. Площадь в геометрии
2. Площадь по координатам вершин или двух определяющих его векторов
3. Площадь в матричном виде
4. Площадь в тензорном исчислении
5. Площадь треугольника в трехмерном пространстве
6. Через проекции площадей на координатные плоскости
7. Использованием операции векторного произведения векторной алгебры
8. Площадь с использованием операций свертки тензорного исчисления

В математике и физике широко пользуются тензорным исчислением, в которой понятия “скаляр”, “вектор” и “тензор” являются широко употребляемыми объектами. Смысл этих понятий и анализ первых двух понятий был определен в предыдущей статье, и последующей . В первой были определены понятия “длины ” вектора и “скалярного” произведения векторов и некоторые определения, с ними связанные, их геометрический смысл, а во второй введены понятия и определения, связанные с тензорами. Без них любая статья подобного направления будет художественным текстом на иностранном языке без перевода.

Под понятием “тензор ” обычно понимаются объекты типа “вектор “, “матрица “, и другие многоиндексные объекты произвольной валентности с размерностью, равной размерности n рассматриваемого пространства:

где i .. j , k .. m – индексы тензора,
m –символ последнего индекса.

Тензоры в математике применяются очень широко. В частности, с их помощью можно определять геометрические параметры – длину, площадь, объем. А также различные “прекции”. А для многомерных объектов – гиперобъемы. Длину вектора или отрезка и проекции мы определили в предыдущих статьях. Здесь определим площади.

1. Площадь в геометрии

Из школьной геометрии мы знаем, что площадь квадрата со сторонами d равна d ² .
Площадь прямоугольника со сторонами a и b равна ab .
Площадь треугольника со стороной a и высотой h равна ah /2.
Площадь треугольника со сторонами a и b равна a · b · sin ( a , b ).

2. Площадь по координатам вершин или двух определяющих его векторов

А чему равна площадь треугольника, заданного с помощью координат ее вершин или двух известных определяющих его сторон–векторов? Конечно, можно вычислить, применяя геометрический метод. Но есть еще один метод – универсальный, годный при любом расположении ее вершин и сторон–векторов. Попробуем найти эту формулу для двумерного случая.

Задача: найти площадь треугольника OAB .

Решение: ACB )площадь треугольника ОАВ равна площади квадрата OYa CXb = Ya Xb за вычетом окружающих треугольник OAB треугольников

S = S(OYb B) + S(BCA) + S(OAXa ).

Вычислим их:

S(OYb B) = (OYb) *(OXb) = Yb Xb,
S(OXa A) = (OXa )*( Ya ) = Xa Ya,
S(BCA) = (Yb – Ya )*( Xa – Xb ) = Yb Xa – Yb Xb – Ya Xa + Ya Xb.

Сложим ( точнее – вычтем ) их :

После приведения подобных членов имеем:

S = ½(Yb Xa – Ya Xb) = A × B.

Это очень замечательная формула, по которой, зная координаты вектора, можно напрямую вычислить площадь треугольника и четырехугольника, построенных на них. При этом получим скалярную – точнее, псевдоскалярную – величину. Псевдоскалярную – потому что, если поменять местами вектора A и B , то результат поменяет свой знак – можете поверить – а можете проверить.

Но у этой формулы имеется недостаток – она годится только на двумерной плоскости.

3. Площадь в матричном виде

Есть еще одна математическая дисциплина, которая позволяет ее методами вычислить площадь треугольника по значениям двух матриц-векторов. В виде формулы она представляется через представление площади как детерминанта матрицы, составленного из элементов этих векторов, в таком виде:

У этой формулы также имеется недостаток – она годится только на двумерной плоскости.

4. Площадь в тензорном исчислении

Эта замечательная формула записана не в тензорном формате. Но она состоит из тензорных элементов, элементы которой определяются как элементы прямого произведения элементов векторов A и B . Для того, чтобы получить скаляр, в тензорном исчислении необходимо свернуть все индексы тензора. Поэтому в тензорном виде площадь записывается в форме, где ε ᵢ ⱼ – антисиммметричный тензор:

5. Площадь треугольника в трехмерном пространстве

В трехмерном случае обойтись такими простыми формулами будет невозможно – алгоритмы будут немножко сложнее. В трехмерном пространстве два вектора будут иметь уже по три координаты – ( x , y , z ). Здесь можно выделить основных метода.

Первый метод – используя двухмерные параметры треугольника – находим соответствующие параметры треугольника (длины сторон, углы, координаты точек A и B в плоскости, где находится треугольник) и применяем любые из выше показанных методов (есть, конечно, и другие методы).

Второй метод – используя непосредственно трехмерные параметры треугольника.

6. Через проекции площадей на координатные плоскости

Например, так. Первой операцией будет нахождение площадей получающегося треугольника в координатных плоскостях S(yz), S(zx) и S(xy). Это можно сделать любым из показанных выше методов. В результате получим проекции площадей треугольника на соответствующие координатные плоскости. Причем три проекции {S(yz), S(zx), S(xy)} составлять координаты некоторого вектора [S(yz), S(zx), S(xy)]. Точнее, опять – псевдовектора или по другому – аксиального вектора . Псевдовектор меняет свой знак при преобразовании отражения осей координат.

А общая площадь получится как длина этого вектора. А длину вектора проходили ранее .

7. Использованием операции векторного произведения векторной алгебры

Есть такая математическая дисциплина, которая называется векторной алгеброй , в которой определена операция 3-мерного векторного умножения, результат которой есть именно определенный только что (п.7) вектор:

C ₃ = A × B = [S(yz), S(zx), S(xy)] = ( Az By – Ay Bz , Ax Bz – Az Bx , Ay Bx – Ax By,) .

А общая площадь получится, как писали там же, как длина этого вектора. Как отмечали выше, этот вектор не совсем обычный – а псевдовектор.

8. Площадь с использованием операций свертки тензорного исчисления

Для этого используем формулу площади треугольника через длину сторон и угол между ними: площадь треугольника со сторонами a и b равна a · b · sin ( a , b ). Найдем участвующие в формуле параметры через скалярные произведения. Длины векторов равны | a | и | b |, а также

В результате получили выражение, состоящее только из скалярных произведений участвующих в формуле параметров треугольника – векторов его сторон a и b. Только в формуле опущены индексы.

И эта формула может быть применена в пространстве любой размерности, а не только размерности 2 и 3.

Если статья понравилась – ставьте лайк, делитесь в ваших соцсетях.
И комментируйте!

Теорема
3.
Пусть точки
,иявляются вершинами треугольника. Тогда
площадь этого треугольника может быть
вычислена по формуле:

.
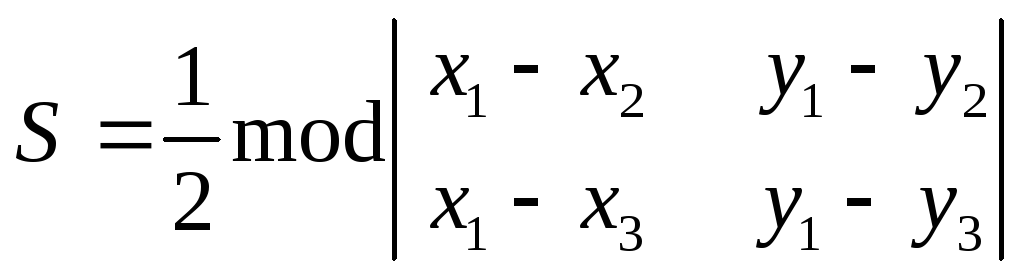
(1.4)

Доказательство.
Рассмотрим треугольник АВС,
расположенный в плоскости Оху.
Площадь этого треугольника равна
разности площадей трапеции К₁АВК₂
и треугольников К₁АС
и СВК₂..
Найдем площадь трапеции К₁АВК₂
и треугольников К₁АС
и СВК₂:

,

,

.

у

В
(х₂;
у₂)

А
(х₁;
у₁)

О

х

К₂
(х₂;
у₃)

К₁
(х₁;
у₃)

С
(х₃;
у₃)

Таким
образом,
.

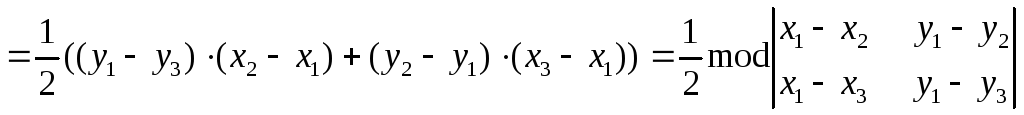
Для
любого другого расположения точек
формула доказывается аналогично. Теорема
доказана.

П
р и м е р 5.
Вычислить площадь параллелограмма
,
если известны координаты его смежных
вершин,и точкипересечения
его диагоналей.

Решение.
Параллелограмм делится диагоналями на
четыре равновеликих треугольника,
поэтому
.
Площадь треугольниканайдем по формуле (1.4):.
Таким образом,(кв. ед.).

П
р и м е р 6.
Одна из вершин треугольника
находится в начале координат, а вторая
вершинаимеет координаты.
Найти координаты третьей вершины,
находящейся на оси ординат, если площадь
треугольникаравна 7 кв. ед.

Решение.
Вершина
находится на оси ординат, поэтому ее
абсцисса равна нулю, т. е. точкаимеет координаты.
Воспользуемся формулой (1.4) для нахождения
площади треугольника, получим:.
Так как площадь треугольникаравна 7 кв. ед., относительнополучаем уравнение,
т. е..
Таким образом, вершинаимеет координатыили.

1.3. Уравнение прямой с угловым коэффициентом

Пусть дана некоторая
прямая.

Определение.
Углом 
наклона данной прямой к оси
называется угол, на который надо повернуть
ось,
чтобы ее положительное направление
совпало с одним из направлений прямой.
Обычно в качестве угла
берут наименьший положительный из
данных углов.

Определение.
Угловым коэффициентом прямой называется
тангенс ее угла наклона, т. е.

.

(1.5)

у

y

M(x, y)

B



N



b

х

C

О

Если

,
то прямая параллельна оси
.
В случаепрямая параллельна оси.

Выведем
уравнение прямой, если известны ее
угловой коэффициент
и величина,
отсекаемая прямой на оси(т. е. прямая не перпендикулярна оси).

Из
треугольника
:.
Далее,,.
Таким образом,,
или

.
(1.6)

Уравнение
(1.6) называется уравнением прямой с
угловым коэффициентом
,
отсекающей на осивеличину.
Если,
то уравнение (1.6) принимает види прямая, задаваемая этим уравнением,
параллельна оси.

Любая
прямая, не параллельная оси
,
задается уравнением вида (1.6), и любое
уравнение вида (1.6) определяет прямую,
не параллельную оси.

1.4. Уравнение прямой, проходящей через данную точку

Выведем
уравнение прямой, проходящей через
точку
,
с угловым коэффициентом.

Прямая
с заданным угловым коэффициентом имеет
уравнение
,
в котором величинанеизвестна. Прямая проходит через точку,
поэтому координаты этой точки
удовлетворяют уравнению прямой, т. е.или.
Следовательно, искомое уравнение имеет
видили

.
(1.7)

Замечание.
Если прямая проходит через точку
параллельно оси,
то ее уравнение имеет вид.

Выведем
уравнение прямой, проходящей через две
заданные точки
и.
Запишем уравнение прямой в виде (1.7):,
где
неизвестный коэффициент. Искомая прямая
проходит через точку
,
поэтому выполняется равенство.

Если
,
то искомая прямая параллельна осии имеет вид.
Если,
тои уравнение (1.7) принимает вид.
В случаепрямая параллельна осии задается уравнением.
Если же,
уравнение прямой, проходящей через две
заданные точки, имеет вид

.
(1.8)

П
р и м е р 7.
Составить уравнение прямой, проходящей
через точку
и составляющей с осью абсцисс угол.

Решение.
По формуле (1.5) угловой коэффициент
прямой
.
Согласно формуле (1.7) искомое уравнение
прямой имеет видили.

П
р и м е р 8. Составить
уравнения сторон треугольника, вершины
которого находятся в точках
,и.

Решение.
Для того чтобы составить уравнения
сторон указанного треугольника,
воспользуемся формулой (1.8) уравнения
прямой, проходящей через две точки с
различными абсциссами и ординатами.
Сторона
задается уравнением,
или.
Для стороныуравнение имеет вид,
или.
Уравнение третьей стороны:,
т. е..

Соседние файлы в папке 20-12-2012_21-26-59

• #
• #
• #
• #
• #
• #
• #