I. Площадь треугольника через синус
 Если в задаче даны длины двух сторон треугольника и угол между ними, то можно применить формулу площади треугольника через синус.
Если в задаче даны длины двух сторон треугольника и угол между ними, то можно применить формулу площади треугольника через синус.
![]() Пример расчета площади треугольника через синус. Даны стороны a = 3, b = 4, и угол γ= 30°. По таблице синусов синус угла в 30° равен 0.5
Пример расчета площади треугольника через синус. Даны стороны a = 3, b = 4, и угол γ= 30°. По таблице синусов синус угла в 30° равен 0.5

Площадь треугольника будет равна 3 кв. см.
| Сторона a= | Сторона b= | Угол γ ° | |
| Ответ: Площадь треугольника = 3.000 |
Также могут быть и другие условия. Если дана длина одной стороны и углы, то для начала нужно вычислить недостающий угол. Т.к. сумма всех углов треугольника равняется 180°, то:
Площадь будет равна половине квадрата стороны, умноженной на дробь. В ее числителе находится произведение синусов прилегающих углов, а в знаменателе синус противолежащего угла. Теперь рассчитываем площадь по следующим формулам:
![]() Например, дан треугольник со стороной a=3 и углами γ=60°, β=60°. Вычисляем третий угол:
Например, дан треугольник со стороной a=3 и углами γ=60°, β=60°. Вычисляем третий угол: 
Подставляем данные в формулу 
Получаем, что площадь треугольника равняется 3,87 кв. см.
II. Площадь треугольника через косинус
Чтобы найти площадь треугольника, нужно знать длины всех сторон. По теореме косинусов можно найти не известные стороны, а уже потом использовать формулу Герона.
По теореме косинусов квадрат неизвестной стороны треугольника равняется сумме квадратов остальных сторон минус удвоенное произведение этих сторон на косинус угла, находящегося между ними.

Из теоремы выводим формулы для поиска длины неизвестной стороны:
Зная как найти недостающую сторону, имея две стороны и угол между ними можно легко посчитать площадь. Формула площади треугольника через косинус помогает легко и быстро найти решение различных задач.
![]() Пример расчета формулы площади треугольника через косинус
Пример расчета формулы площади треугольника через косинус
Дан треугольник с известными сторонами a = 3, b = 4, и углом γ= 45°. Для начала найдем недостающую сторону с. По таблице косинусов косинус 45°=0,7. Для этого подставим данные в уравнение, выведенное из теоремы косинусов. 
Теперь используя формулу, найдем площадь треугольника по трем сторонам:



| Сторона a= | Сторона b= | Угол γ ° | |
| Ответ: Площадь треугольника = 4.243 |
Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона
Формула Герона для нахождения площади треугольника:
Через основание и высоту
Формула нахождения площади треугольника с помощью половины его основания и высоту:
Через две стороны и угол
Формула нахождения площади треугольника через две стороны и угол между ними:
Через сторону и два прилежащих угла
Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
Площадь прямоугольного треугольника
Прямоугольный треугольник – треугольник у которого один из углов прямой, т.е. равен 90°.
Формула нахождения площади прямоугольного треугольника через катеты:
Площадь равнобедренного треугольника через стороны
Равнобедренный треугольник – треугольник, в котором две стороны равны. А значит, равны и два угла.
Формула нахождения площади равнобедренного треугольника через две стороны:
Площадь равнобедренного треугольника через основание и угол
Формула нахождения площади равнобедренного треугольника через основание и угол:
Площадь равностороннего треугольника через стороны
Равносторонний треугольник – треугольник, в котором все стороны равны, а каждый угол равен 60°.
Формула нахождения площади равностороннего треугольника через сторону:
Площадь равностороннего треугольника через высоту
Формула нахождения площади равностороннего треугольника через высоту:
Площадь равностороннего треугольника через радиус вписанной окружности
Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
Площадь равностороннего треугольника через радиус описанной окружности
Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
Площадь треугольника через радиус описанной окружности и три стороны
Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
Площадь треугольника через радиус вписанной окружности и три стороны
Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
Теория и практика по треугольникам (Часть Ⅱ)
 Площадь треугольников.
Площадь треугольников.
Тригонометрия в прямоугольных треугольниках.
Что такое синус/косинус.
Таблицы Брадиса. Как пользоваться.
Теорема синусов и косинусов.
Геометрия — это искусство хорошо рассуждать на плохо выполненных чертежах.
С основными свойствами разобрались, теперь рассмотрим формулы и их приминение.
Площадь произвольного треугольника
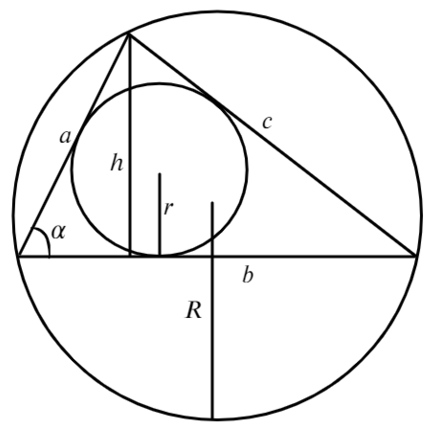
Нет, это не кривая пентаграмма, нужны на этом рисунке только обозначения. Рассмотрим формулы школьной программы.
Высоту умножаем на ту сторону, на которую приходит высота:
В эту формулу подставляем угол между сторонами a и b:
Удобно использовать эту формулу, когда известны все стороны треугольника, p — полупериметр (половина суммы длин всех сторон):
Данная формула отлично помогает найти радиус вписанной окружности для любого треугольника, если известна площадь:
А эта формула помогает найти радиус описанной окружности для любого треугольника:
А зачем такое количество формул? К каждой задаче будут предоставлять разное дано, удобно знать и применять все формулы, чтобы максимально быстро решать задачи.
Полезные формулы для прямоугольного и равностороннего треугольника:
В данном случае получается, что один катет «b» — высота треугольника, а катет «а» — основание.
Эту формулу можно вывести большим количеством способов, самый простой через формулу №2
Задача №1. Дано на рисунке:
Оттолкнемся от вопроса: нужно найти площадь. Помимо 5 формул для произвольного треугольника, нам подойдет формула нахождения площади через полупроизведение катетов.
Вариантов здесь много (можно через т. Пифагора), но самый быстрый — найти ∠А = 180°− 90° − 60° = 30°, тогда площадь найдем по (2) формуле: S = ½absinα
Ответ: 60
Задача №2. Дано на рисунке:
Снова оттолкнемся от вопроса: нужно найти площадь. Дан обычный треугольник, значит, наш выбор ограничен первыми 5−ью формулами. В первой нужна высота, во второй угол, а в третьей полупериметр, но мы же знаем все стороны! Для начала найдем периметр и полупериметр:
Теперь можно подставить все числа в формулу площади:
Главное — правильно определиться с формулой.
Задача №3. Дано на рисунке:
В ΔABH: ∠A = 180°− 90° − 45° = 45°, значит, ∠A = ∠B => BH = AH = 12.
Тогда площадь можно найти по формуле (1) S=½bh. Высота AH = 12, основание AC = 16+12 = 28. => S = ½×12×28 = 168
Задача №4. Дано на рисунке:
Оттолкнемся от отношения, которое нам дано. Мы знаем, что сумма данных углов равна 90°, если ∠ACM = х и ∠ВCM = 2х, тогда 2х+х = 90°
∠ACM = х = 30° => ∠ВCM = 60°. А что у нас равно 4-ем? Да, медиана! А медиана, проведенная из прямого угла, равна половине гипотенузы (2−ое свойство). Тогда отметим равные углы:
В ΔBCM получается ∠ВCM = ∠СВM = 60°, тогда ∠СМВ = 60° и ΔBCM — правильный:
Площадь найдем по (2) формуле: S = ½absinα:
Задача №5. Дано на рисунке:
В дано есть только стороны, а найти нужно угол. Как это сделать? Вот стороны 14,2 и 7,1 во сколько раз отличаются? Да, в 2 раза, а значит угол ∠BAL = 30° (против угла в 30° лежит катет, который в два раза меньше гипотенузы).
Значит, ∠A = 60° => ∠ACB = 180° − 90° − 60° = 30°, а ∠ACB — смежный с ∠ACV => ∠ACV = 180° − 30° = 150°.
Что касается LC: внимательно рассмотрим ΔALC, можно даже лупой воспользоваться. Что видишь? ∠LAC = ∠ACL = 30° => ΔALC — равнобедренный, LC = AL = 14,2.
Ответ: 14,2 и 150°
Тригонометрия в прямоугольных треугольниках
В прямоугольном треугольнике три стороны: 2 катета и гипотенуза.
Катеты меньшие стороны треугольника. Гипотенуза большая сторона, которая лежит напротив угла в 90°.
Относительно угла α:
Катет, который составляет угол, называют прилежащим. Катет, который находится напротив угла, называют противолежащим. Логично? Замечательно!
Тригонометрические функции (синус, косинус. ) задают связь между углом и длинами сторон.
Но хорошо бы знать какие-то значения тригонометрических функций при определенных углах. Все значения вместе образуют таблицу Брадиса. С ее помощью можно вычислить почти любое значение тригонометрической функции при заданом угле. Но как с ней работать?
Найдем sin(10°) . Для этого выберем столбец sin и в нем найдем 10°. Ближайшее значение — это то, что нам нужно — 0,1736.
А что за столбец 0′; 6′; 12′ и т.д. Это минуты! Не те, которых мы ждем в конце урока, а градусные минуты.
Из общего: и те, и другие минуты измеряются в промежутке от 0 до 60.
Градусные минуты делят один градус на 60 минут (1°=60′), нужны они для большей точности задания угла.
p.s. Есть еще и градусные секунды, и в одной градусной минуте 60 градусных секунд, знакомо? 1° = 60′ = 3600”.
Семь десятых градуса нужно перевести в минуты. Можно через пропорцию:
Теперь в таблице нужно найти 77°42′ для косинуса. Для синуса минуты прописаны, а для косинуса нет. Но мы же люди не гордые, сами напишем, но в обратном порядке. На пересечении 77° и 42′ получаем наше значение:
Но чтобы не загромождать таблицу 0, его в начале пишут только в первых строчках, поэтому ответ cos(77,7°) = 0,213.
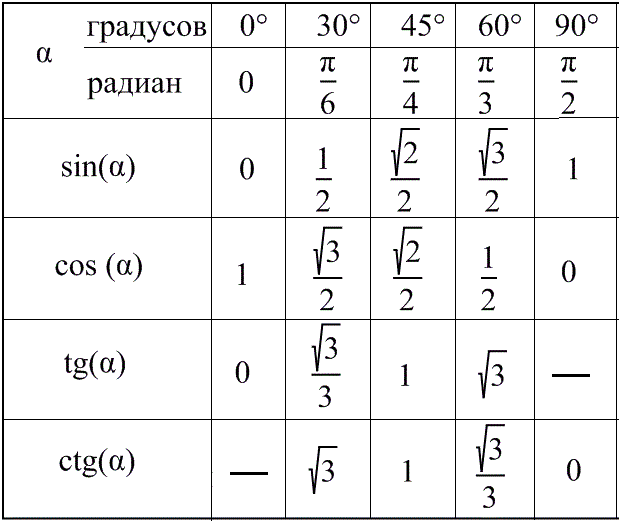
В задачах же таким обилием углов похвастаться нельзя, достаточно знать значения для 30°; 45°; 60°; 90°.
Искусство решать геометрические задачи чем-то напоминает трюки иллюзионистов — иногда,
даже зная решение задачи, трудно понять, как можно было до него додуматься.
Задача №6. Дано на рисунке:
В этой задаче известен противолежащий катет относительно угла в 45°, а найти нужно гипотенузу. Смотрим, где у нас есть противполежащий катет и гипотенуза? Это синус!
Смотрим в таблице, чему равен синус 45°, и подставляем в отношение:
Задача №7. Дано на рисунке:
Мы разобрались с тригонометрическими функциями в прямоугольных треугольниках, значит, и в этой задаче нужно перейти к прямоугольному треугольнику.
В ΔLTK — равнобедренный : ∠L = ∠LKT = (180° − 120°)/2 = 30°
Отлично, в прямоугольном ΔLVK: ∠L = 30° и известна гипотенуза, а нам нужно найти противолежащий катет, чем воспользуемся? Опять синусом!
Теорема синусов и теорема косинусов
Сразу возникает вопрос, а теорема тангенсов тоже есть? Конечно, есть, но она очень редко используется.
Для любого треугольника можно записать такое соотношение, это будет теорема синусов:
Запомни, что сторона относится к синусу противолежащего угла.
Следствие из теорма синусов гласит, что любое соотношение равно двум радиусам описанной окружности:
Для любого треугольника можно записать такое соотношение, это будет теорема косинусов:
А что будет, если α = 90°, а cos(90) = 0? Получится:
Теорема Пифагора, вот так просто можно запомнить теорему косинусов. Начать как теорему Пифагора, а затем вычесть удвоенное произведение на косинус угла между ними.
Можно записать и для других сторон в этом же треугольнике:
Задача №8. Дано на рисунке:
Запишем теорему синусов для двух отношений:
Выразим отсюда KT:
∠K = 180° − 60° − 45° = 75°. Чтобы найти синус угла 75°, советую посмотреть эту статью, нужно воспользовать формулой суммы синусов:
Тогда представим 75° в виде двух табличных значений:
Аналогично выразим LT:
Ответ: 16,3 и 22,3
Задача №9. Дано на рисунке:
Найти нужно x и y. Запишем теорему косинусов для этого треугольника:
Икс выразим через игрек:
Отлично, поздравляю тебя с Elementary по геометрии!
Что нужно знать:
- Вертикальные, смежные, соответственные, накрест лежащие углы.
- Равенство и подобие треугольников.
- Что такое медиана, биссектриса, высота.
- Свойства треугольников.
- Площадь треугольников.
- Синус/косинус в треугольнике.
- Теорему синусов и косинусов.
Как найти площадь треугольника
О чем эта статья:
8 класс, 9 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
Площадь — это численная характеристика, которая дает нам информацию о размере части плоскости, ограниченной замкнутой геометрической фигурой.
Если значения заданы в разных единицах измерения длины, мы не сможем узнать, какая площадь треугольника получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
Популярные единицы измерения площади:
- квадратный миллиметр (мм 2 );
- квадратный сантиметр (см 2 );
- квадратный дециметр (дм 2 );
- квадратный метр (м 2 );
- квадратный километр (км 2 );
- гектар (га).
Формула площади треугольника
Для решения задач применяются различные формулы, в зависимости от известных исходных данных. Далее мы рассмотрим способы решения для всех типов треугольников, в том числе частные случаи для равносторонних, равнобедренных и прямоугольных фигур.
Быстро вычислить площадь треугольника поможет наш онлайн-калькулятор. Просто введите известные вам значения и получите ответ в метрах, сантиметрах или миллиметрах.
Научиться быстро щелкать задачки на нахождение площади треугольника помогут курсы по математике от Skysmart!
Общая формула
1. Площадь треугольника через основание и высоту
, где — основание, — высота.
2. Площадь треугольника через две стороны и угол между ними
, где , — стороны, — угол между ними.
3. Площадь треугольника через описанную окружность и стороны
, где , , — стороны, — радиус описанной окружности.
4. Площадь треугольника через вписанную окружность и стороны
, где , , — стороны, — радиус вписанной окружности.
Если учитывать, что — это способ поиска полупериметра, то формулу можно записать следующим образом:
5. Площадь треугольника по стороне и двум прилежащим углам
, где — сторона, и — прилежащие углы.
6. Формула Герона для вычисления площади треугольника
Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.
, где , , — стороны, — полупериметр, который можно найти по формуле:
Для прямоугольного треугольника
Площадь треугольника с углом 90° по двум сторонам
Площадь треугольника по гипотенузе и острому углу
, где — гипотенуза, — любой из прилегающих острых углов.
Гипотенузой принято называть сторону, которая лежит напротив прямого угла.
Площадь прямоугольного треугольника по катету и прилежащему углу
, где — катет, — прилежащий угол.
Катетом принято называть одну из двух сторон, образующих прямой угол.
Площадь треугольника через гипотенузу и радиус вписанной окружности
, где — гипотенуза, — радиус вписанной окружности.
Площадь треугольника по отрезкам, на которые делит вписанная окружность его гипотенузу
, где , — части гипотенузы.
Площадь прямоугольного треугольника по формуле Герона
, где , — катеты, — полупериметр, который можно найти по формуле:
Для равнобедренного треугольника
Вычисление площади через основание и высоту
, где — основание, — высота, проведенная к основанию.
Поиск площади через боковые стороны и угол между ними
, где — боковая сторона, — угол между боковыми сторонами.
Площадь равностороннего треугольника через радиус описанной окружности
, где — радиус описанной окружности.
Площадь равностороннего треугольника через радиус вписанной окружности
, где — радиус вписанной окружности.
Площадь равностороннего треугольника через сторону
Площадь равностороннего треугольника через высоту
Таблица формул нахождения площади треугольника
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу, использовать как закладку в тетрадке или учебнике и обращаться к ней по необходимости.
[spoiler title=”источники:”]
http://ik-study.ru/ege_math/tieoriia_i_praktika_po_trieughol_nikam_chast_ii_
http://skysmart.ru/articles/mathematic/ploshad-treugolnika
[/spoiler]

Стандартные обозначения углов и сторон треугольника
Теорема косинусов — теорема евклидовой геометрии, обобщающая теорему Пифагора на произвольные плоские треугольники.
Формулировка[править | править код]
Для плоского треугольника со сторонами 


справедливо соотношение:
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними[1]
Доказательства[править | править код]
Классическое доказательство

Рассмотрим треугольник ABC. Из вершины C на сторону AB опущена высота CD. Из треугольника ADC следует:
,
откуда
.
Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
Приравниваем правые части уравнений (1) и (2) и:
или
.
Случай, когда один из углов при основании тупой (и высота падает на продолжение основания), полностью аналогичен рассмотренному.
Выражения для сторон b и c:
.
Доказательство через координаты
Одним из доказательств является доказательство её в координатной плоскости.
Внесём в координатную плоскость произвольный треугольник ABC так, чтобы точка А совпала с началом координат, а прямая АВ лежала на прямой ОХ. Введём обозначения AB=c, AC=b, CB=a, a угол CAB=α(пока будем считать что α≠90°).
Тогда точка A имеет координаты (0;0), точка B(c;0). Через функцию sin и cos, а также сторону АС=b выведем координаты точки С. С(b×cosα;b×sinα).
Координаты точки С остаются неизменными при тупом и остром угле α.
Зная координаты С и B, а также зная, что CB=a, найдя длину отрезка, мы можем составить равенство:
Так как

Теорема доказана.
Для прямого угла α, теорема также работает cos90°=0 и a²=b²+с² – известная всем теорема Пифагора. Но так как в основе координатного метода лежит теорема Пифагора, то доказательство её через теорему косинусов не совсем правильно.
Доказательство через векторы
Ниже подразумеваются операции над векторами, а не длинами отрезков

Так как скалярное произведение векторов равно произведению их модулей (длин) на косинус угла между ними, последнее выражение можно переписать:
где a, b, c — длины соответствующих векторов
Следствия[править | править код]
- Теорема косинусов может быть использована для нахождения косинуса угла треугольника
- В частности,
- Теорема косинусов может быть записана также в следующем виде[2]:
,
.
Доказательство
Последние две формулы мгновенно следуют из основной формулы теоремы косинусов (см. в рамке выше), если в правой её части воспользоваться формулами разложения квадрата суммы (для второй формулы – квадрата разности) двух членов на квадратный трехчлен, являющийся полным квадратом. Для получения окончательного результата (двух формул выше) в правой части надо еще воспользоваться известными тригонометрическими формулами:
,
.
Кстати, вторая формула формально не содержит косинусов, но её все равно именуют теоремой косинусов.
Для других углов[править | править код]
Теорема косинусов для двух других углов имеет вид:
Из этих и из основной формулы могут быть выражены углы:
История[править | править код]
Утверждения, обобщающие теорему Пифагора и эквивалентные теореме косинусов, были сформулированы отдельно для случаев острого и тупого угла в 12 и 13 предложениях II книги «Начал» Евклида.
Утверждения, эквивалентные теореме косинусов для сферического треугольника, применялись в сочинениях ал-Баттани.[3]:105
Теорему косинусов для сферического треугольника в привычном нам виде сформулировал Региомонтан, назвав её «теоремой Альбатегния» по имени ал-Баттани.
В Европе теорему косинусов популяризовал Франсуа Виет в XVI столетии.
В начале XIX столетия её стали записывать в принятых по сей день алгебраических обозначениях.
Вариации и обобщения[править | править код]
- Теоремы косинусов (сферическая геометрия) или Теорема косинусов для трёхгранного угла.
- Теоремы косинусов (геометрия Лобачевского)
- Тождество параллелограмма. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон (см. также Теорема Птолемея):
Для евклидовых нормированных пространств[править | править код]
Пусть в евклидовом пространстве 

Теорема.

Для четырёхугольников[править | править код]
Возводя в квадрат тождество 
, где
— угол между прямыми AB и CD.
Или иначе:
- Формула справедлива и для тетраэдра, под
подразумевается угол между скрещивающимися ребрами.
- С помощью неё можно найти косинус угла между скрещивающимися ребрами
и
зная все ребра тетраэдра:
- Где
и
,
и
пары скрещивающихся ребер тетраэдра.
Косвенный аналог для четырёхугольника[править | править код]

Соотношение Бретшнайдера — соотношение в четырёхугольнике, косвенный аналог теоремы косинусов:
Между сторонами a, b, c, d и противоположными углами
и диагоналями e, f простого (несамопересекающегося) четырёхугольника выполняется соотношение:
- Если четырёхугольник вырождается в треугольник, и одна вершина попадает на сторону, то получается теорема Стюарта.
- Теорема косинусов для треугольника является частным случаем соотношения Бретшнайдера, если в качестве четвёртой вершины выбрать центр описанной окружности треугольника.
Симплексы[править | править код]
при этом мы должны зачеркнуть строку и столбец, где находится 

A — угол между гранями 



См. также[править | править код]
- Решение треугольников
- Скалярное произведение
- Соотношение Бретшнайдера
- Теорема косинусов для трёхгранного угла
- Теорема о проекциях
- Теорема Пифагора
- Сферическая теорема косинусов
- Теорема котангенсов
- Теорема синусов
- Теорема тангенсов
- Тригонометрические тождества
- Тригонометрические функции
Примечания[править | править код]
- ↑ Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия 7—9: учеб. для общеобразоват. учреждений — 15-е изд. — М.: Просвещение, 2005. — С. 257. — 384 с.: ил. — ISBN 5-09-014398-6
- ↑ 1 2 Корн Г. А., Корн Т. М. Справочник по математике для научных работников и инженеров. — М.: «Наука», 1974. — С. 51. — 832 с.
- ↑ Florian Cajori. A History of Mathematics — 5th edition 1991
Литература[править | править код]
- Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 84—85. — ISBN 5-94057-170-0.
 Площадь треугольников.
Площадь треугольников.
Свойства треугольников.
Тригонометрия в прямоугольных треугольниках.
Что такое синус/косинус.
Таблицы Брадиса. Как пользоваться.
Теорема синусов и косинусов.
Геометрия — это искусство хорошо рассуждать на плохо выполненных чертежах.
Г. Абель
С основными свойствами разобрались, теперь рассмотрим формулы и их приминение.
Площадь произвольного треугольника

Нет, это не кривая пентаграмма, нужны на этом рисунке только обозначения. Рассмотрим формулы школьной программы.
 Высоту умножаем на ту сторону, на которую приходит высота:
Высоту умножаем на ту сторону, на которую приходит высота: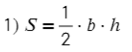 В эту формулу подставляем угол между сторонами a и b:
В эту формулу подставляем угол между сторонами a и b:
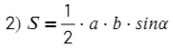 Удобно использовать эту формулу, когда известны все стороны треугольника, p — полупериметр (половина суммы длин всех сторон):
Удобно использовать эту формулу, когда известны все стороны треугольника, p — полупериметр (половина суммы длин всех сторон):
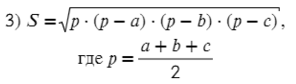 Данная формула отлично помогает найти радиус вписанной окружности для любого треугольника, если известна площадь:
Данная формула отлично помогает найти радиус вписанной окружности для любого треугольника, если известна площадь:
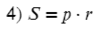 А эта формула помогает найти радиус описанной окружности для любого треугольника:
А эта формула помогает найти радиус описанной окружности для любого треугольника:
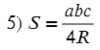 А зачем такое количество формул? К каждой задаче будут предоставлять разное дано, удобно знать и применять все формулы, чтобы максимально быстро решать задачи.
А зачем такое количество формул? К каждой задаче будут предоставлять разное дано, удобно знать и применять все формулы, чтобы максимально быстро решать задачи.
Полезные формулы для прямоугольного и равностороннего треугольника:
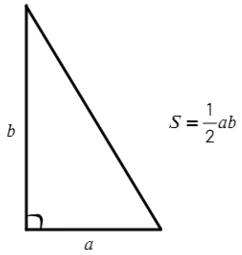 В данном случае получается, что один катет «b» — высота треугольника, а катет «а» — основание.
В данном случае получается, что один катет «b» — высота треугольника, а катет «а» — основание.
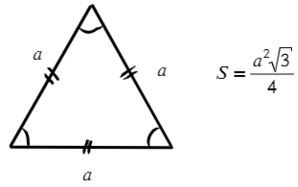 Эту формулу можно вывести большим количеством способов, самый простой через формулу №2
Эту формулу можно вывести большим количеством способов, самый простой через формулу №2
Задача №1. Дано на рисунке:
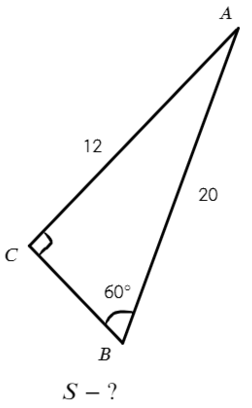 Оттолкнемся от вопроса: нужно найти площадь. Помимо 5 формул для произвольного треугольника, нам подойдет формула нахождения площади через полупроизведение катетов.
Оттолкнемся от вопроса: нужно найти площадь. Помимо 5 формул для произвольного треугольника, нам подойдет формула нахождения площади через полупроизведение катетов.
Вариантов здесь много (можно через т. Пифагора), но самый быстрый — найти ∠А = 180°− 90° − 60° = 30°, тогда площадь найдем по (2) формуле: S = ½absinα
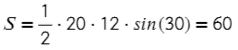 Ответ: 60
Ответ: 60
Задача №2. Дано на рисунке:
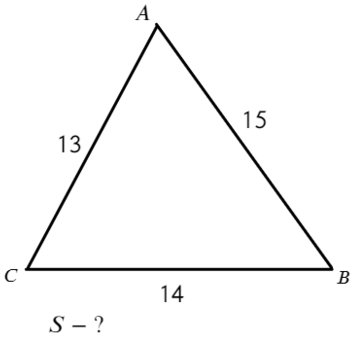 Снова оттолкнемся от вопроса: нужно найти площадь. Дан обычный треугольник, значит, наш выбор ограничен первыми 5−ью формулами. В первой нужна высота, во второй угол, а в третьей полупериметр, но мы же знаем все стороны! Для начала найдем периметр и полупериметр:
Снова оттолкнемся от вопроса: нужно найти площадь. Дан обычный треугольник, значит, наш выбор ограничен первыми 5−ью формулами. В первой нужна высота, во второй угол, а в третьей полупериметр, но мы же знаем все стороны! Для начала найдем периметр и полупериметр:
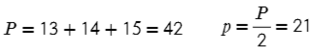 Теперь можно подставить все числа в формулу площади:
Теперь можно подставить все числа в формулу площади:
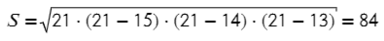
Главное — правильно определиться с формулой.
Ответ: 84
Задача №3. Дано на рисунке:
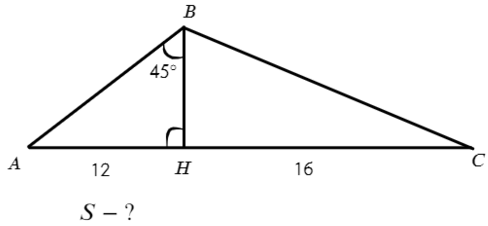
В ΔABH: ∠A = 180°− 90° − 45° = 45°, значит, ∠A = ∠B => BH = AH = 12.
Тогда площадь можно найти по формуле (1) S=½bh. Высота AH = 12, основание AC = 16+12 = 28. => S = ½×12×28 = 168
Ответ: 168.
Задача №4. Дано на рисунке:
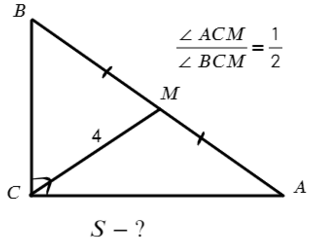 Оттолкнемся от отношения, которое нам дано. Мы знаем, что сумма данных углов равна 90°, если ∠ACM = х и ∠ВCM = 2х, тогда 2х+х = 90°
Оттолкнемся от отношения, которое нам дано. Мы знаем, что сумма данных углов равна 90°, если ∠ACM = х и ∠ВCM = 2х, тогда 2х+х = 90°
∠ACM = х = 30° => ∠ВCM = 60°. А что у нас равно 4-ем? Да, медиана! А медиана, проведенная из прямого угла, равна половине гипотенузы (2−ое свойство). Тогда отметим равные углы:
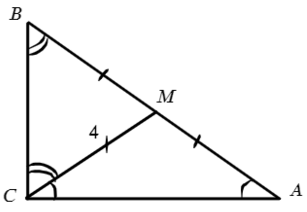 В ΔBCM получается ∠ВCM = ∠СВM = 60°, тогда ∠СМВ = 60° и ΔBCM — правильный:
В ΔBCM получается ∠ВCM = ∠СВM = 60°, тогда ∠СМВ = 60° и ΔBCM — правильный:
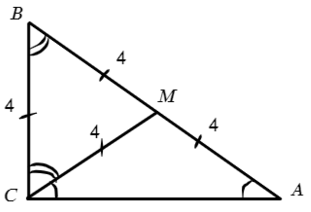 Площадь найдем по (2) формуле: S = ½absinα:
Площадь найдем по (2) формуле: S = ½absinα:
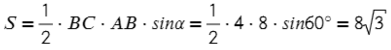
Ответ: 8√3
Задача №5. Дано на рисунке:
В дано есть только стороны, а найти нужно угол. Как это сделать? Вот стороны 14,2 и 7,1 во сколько раз отличаются? Да, в 2 раза, а значит угол ∠BAL = 30° (против угла в 30° лежит катет, который в два раза меньше гипотенузы).
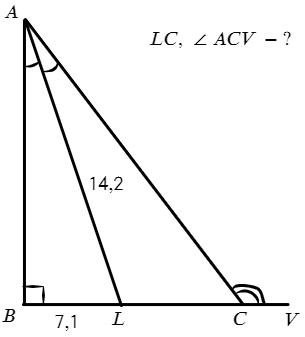
Значит, ∠A = 60° => ∠ACB = 180° − 90° − 60° = 30°, а ∠ACB — смежный с ∠ACV => ∠ACV = 180° − 30° = 150°.
Что касается LC: внимательно рассмотрим ΔALC, можно даже лупой воспользоваться. Что видишь? ∠LAC = ∠ACL = 30° => ΔALC — равнобедренный, LC = AL = 14,2.
Ответ: 14,2 и 150°
Тригонометрия в прямоугольных треугольниках
В прямоугольном треугольнике три стороны: 2 катета и гипотенуза.
Катеты меньшие стороны треугольника. Гипотенуза большая сторона, которая лежит напротив угла в 90°.
Относительно угла α:
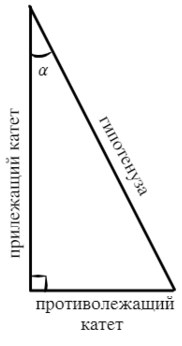
Катет, который составляет угол, называют прилежащим. Катет, который находится напротив угла, называют противолежащим. Логично? Замечательно!
Тригонометрические функции (синус, косинус…) задают связь между углом и длинами сторон.

Но хорошо бы знать какие-то значения тригонометрических функций при определенных углах. Все значения вместе образуют таблицу Брадиса. С ее помощью можно вычислить почти любое значение тригонометрической функции при заданом угле. Но как с ней работать?
Найдем sin(10°). Для этого выберем столбец sin и в нем найдем 10°. Ближайшее значение — это то, что нам нужно — 0,1736.
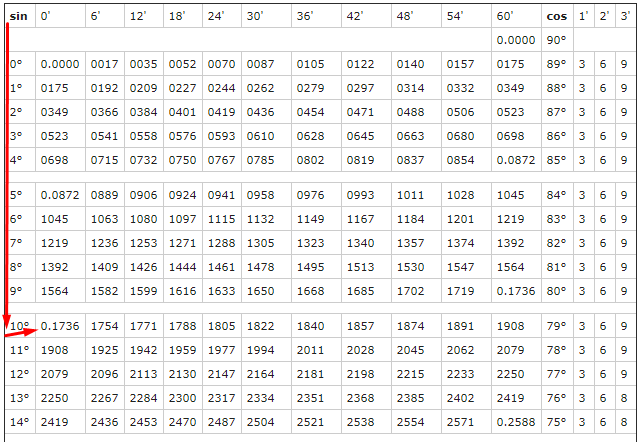 А что за столбец 0′; 6′; 12′ и т.д. Это минуты! Не те, которых мы ждем в конце урока, а градусные минуты.
А что за столбец 0′; 6′; 12′ и т.д. Это минуты! Не те, которых мы ждем в конце урока, а градусные минуты.
Из общего: и те, и другие минуты измеряются в промежутке от 0 до 60.
Градусные минуты делят один градус на 60 минут (1°=60′), нужны они для большей точности задания угла.
p.s. Есть еще и градусные секунды, и в одной градусной минуте 60 градусных секунд, знакомо? 1° = 60′ = 3600”.
Найдем cos(77,7°)
Семь десятых градуса нужно перевести в минуты. Можно через пропорцию:
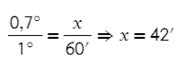
Теперь в таблице нужно найти 77°42′ для косинуса. Для синуса минуты прописаны, а для косинуса нет. Но мы же люди не гордые, сами напишем, но в обратном порядке. На пересечении 77° и 42′ получаем наше значение:
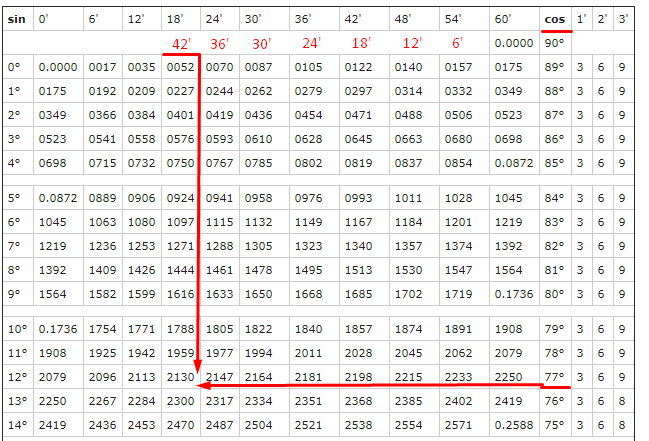
Но чтобы не загромождать таблицу 0, его в начале пишут только в первых строчках, поэтому ответ cos(77,7°) = 0,213.
В задачах же таким обилием углов похвастаться нельзя, достаточно знать значения для 30°; 45°; 60°; 90°.
Искусство решать геометрические задачи чем-то напоминает трюки иллюзионистов — иногда,
даже зная решение задачи, трудно понять, как можно было до него додуматься.
И.Д. Новиков
Задача №6. Дано на рисунке:
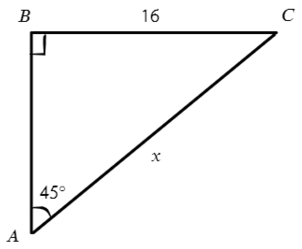
В этой задаче известен противолежащий катет относительно угла в 45°, а найти нужно гипотенузу. Смотрим, где у нас есть противполежащий катет и гипотенуза? Это синус!
Смотрим в таблице, чему равен синус 45°, и подставляем в отношение:
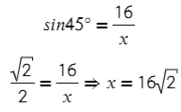
Ответ: 16√2
Задача №7. Дано на рисунке:
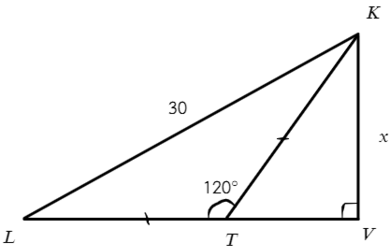
Мы разобрались с тригонометрическими функциями в прямоугольных треугольниках, значит, и в этой задаче нужно перейти к прямоугольному треугольнику.
В ΔLTK — равнобедренный : ∠L = ∠LKT = (180° − 120°)/2 = 30°
Отлично, в прямоугольном ΔLVK: ∠L = 30° и известна гипотенуза, а нам нужно найти противолежащий катет, чем воспользуемся? Опять синусом!
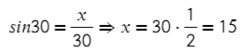
Ответ: 15
Теорема синусов и теорема косинусов
Сразу возникает вопрос, а теорема тангенсов тоже есть? Конечно, есть, но она очень редко используется.
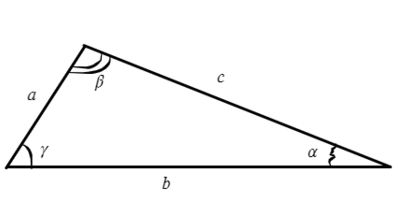
Для любого треугольника можно записать такое соотношение, это будет теорема синусов:
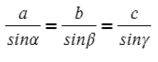
Запомни, что сторона относится к синусу противолежащего угла.
Следствие из теорма синусов гласит, что любое соотношение равно двум радиусам описанной окружности:
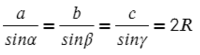
Для любого треугольника можно записать такое соотношение, это будет теорема косинусов:
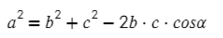
А что будет, если α = 90°, а cos(90) = 0? Получится:
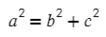
Теорема Пифагора, вот так просто можно запомнить теорему косинусов. Начать как теорему Пифагора, а затем вычесть удвоенное произведение на косинус угла между ними.
Можно записать и для других сторон в этом же треугольнике:
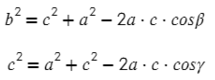
Задача №8. Дано на рисунке:
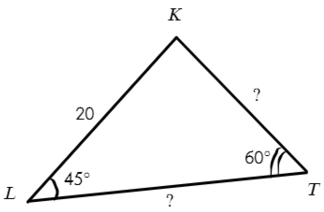
Запишем теорему синусов для двух отношений:
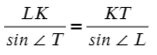
Выразим отсюда KT:
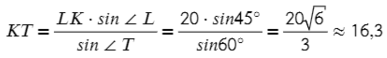
∠K = 180° − 60° − 45° = 75°. Чтобы найти синус угла 75°, советую посмотреть эту статью, нужно воспользовать формулой суммы синусов:
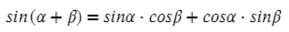
Тогда представим 75° в виде двух табличных значений:
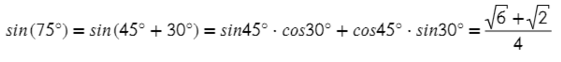
Аналогично выразим LT:
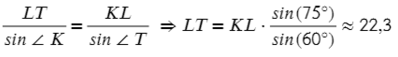
Ответ: 16,3 и 22,3
Задача №9. Дано на рисунке:
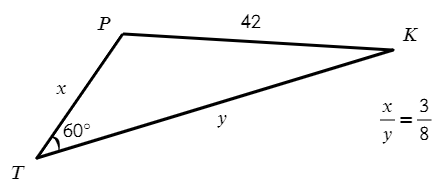
Найти нужно x и y. Запишем теорему косинусов для этого треугольника:
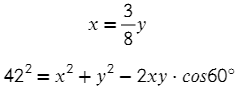
Икс выразим через игрек:
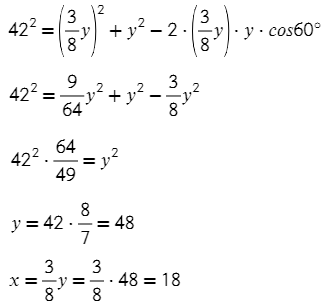
Ответ: 48; 18
Отлично, поздравляю тебя с Elementary по геометрии!
Что нужно знать:
- Вертикальные, смежные, соответственные, накрест лежащие углы.
- Равенство и подобие треугольников.
- Что такое медиана, биссектриса, высота.
- Свойства треугольников.
- Площадь треугольников.
- Синус/косинус в треугольнике.
- Теорему синусов и косинусов.
Задачи для закрепления по треугольникам
Нашел опечатку, или что-то непонятно — напиши.
Группа с полезной информацией и легким математическим юмором.
Лучший ответ
Люся Люсяо
Просветленный
(34549)
12 лет назад
Теорема косинусов:
a^2 = b^2+c^2-2*b*c*cos(alpha)
b, c – твои стороны, alpha – угол между ними.
Если alpha в градусах, то сначала переводим в радианы
alpha := alpha*pi/180;
a := sqrt(b*b+c*c-2*b*c*cos(alpha));
P.S. Учите математику, иногда помогает 🙂
Михаил СеменихинУченик (148)
2 года назад
спасибо
Остальные ответы
V8
Гуру
(3717)
12 лет назад
ну именно этой формулы я не помню я бы по теореме косинусов нашел третью, а дальше через формулу герона нашел бы площадь
Семен Аркадьевич
Высший разум
(340149)
12 лет назад
Можно значительно проще. Зная косинус, найдите синус (основное тригонометрическое тождество)
А теперь можно применить известную формулу площади.
Михаил СеменихинУченик (148)
2 года назад
да ваше легче






























