Выясним, как связаны средняя линия треугольника и его площадь.
 I. Площадь треугольника равна половине произведения основания на высоту, проведённую к этой стороне:
I. Площадь треугольника равна половине произведения основания на высоту, проведённую к этой стороне:
![]()
Поскольку средняя линия треугольника, соединяющая середины двух сторон, равна половине третьей стороны:
![]()
то можно найти площадь треугольника через его среднюю линию:
![]()
Вывод:
Площадь треугольника равна произведению средней линии и высоты, перпендикулярной этой средней линии.
II.Прямая, параллельная стороне треугольника и пересекающая две другие его стороны, отсекает от него подобный треугольник.
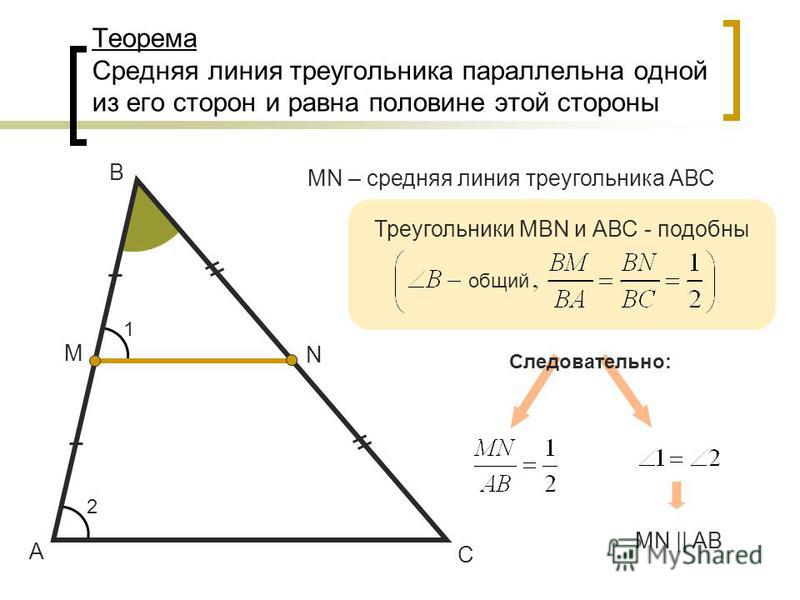
 Если MN- средняя линия треугольника ABC и MN параллельна AC, то треугольники ABC и MBN подобны.
Если MN- средняя линия треугольника ABC и MN параллельна AC, то треугольники ABC и MBN подобны.
Поскольку
![]()
то
![]()
Так как площади подобных треугольников относятся как квадраты их соответствующих сторон, то
![]()
то есть
![]()
Вывод:
Средняя линия треугольника отсекает от него треугольник, площадь которого равна четверти площади исходного треугольника.
Например, если площадь треугольника ABC равна 40 см², то средняя линия MN, параллельная стороне AC, делит его площадь на части:
![]()
Площадь трапеции AMNC составляет три четверти площади треугольника ABC
![]()
или может быть найденакак разность площадей треугольников ABC и MBC.
На чтение 4 мин Просмотров 2.2к. Опубликовано 04.07.2019
Содержание
- Содержание
- Средняя линия треугольника [ править | править код ]
- Свойства [ править | править код ]
- Признаки [ править | править код ]
- Средняя линия четырёхугольника [ править | править код ]
- Свойства [ править | править код ]
- Средняя линия трапеции [ править | править код ]
Средняя линия фигур в планиметрии — отрезок, соединяющий середины двух сторон данной фигуры. Понятие употребляется для следующих фигур: треугольник, четырёхугольник, трапеция.
Содержание
Средняя линия треугольника [ править | править код ]

Средняя линия треугольника — отрезок, соединяющий середины двух сторон этого треугольника [1] .
Свойства [ править | править код ]
- средняя линия треугольника параллельна основанию и равна его половине.
- средняя линия отсекает треугольник, подобный и гомотетичный исходному с коэффициентом 1/2; его площадь равна одной четвёртой площади исходного треугольника.
- три средние линии делят исходный треугольник на четыре равных треугольника. Центральный из этих треугольников называется дополнительным или серединным треугольником.
Признаки [ править | править код ]
- Если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей, то этот отрезок – средняя линия.
Средняя линия четырёхугольника [ править | править код ]
Средняя линия четырёхугольника — отрезок, соединяющий середины противолежащих сторон четырёхугольника.
Свойства [ править | править код ]
Первая линия соединяет 2 противоположные стороны. Вторая соединяет 2 другие противоположные стороны. Третья соединяет центры двух диагоналей (не во всех четырёхугольниках диагонали пунктом пересечения делятся пополам).
- Если в выпуклом четырёхугольнике средняя линия образует равные углы с диагоналями четырёхугольника, то диагонали равны.
- Длина средней линии четырёхугольника меньше полусуммы двух других сторон или равна ей, если эти стороны параллельны, и только в этом случае.
- Середины сторон произвольного четырёхугольника — вершины параллелограмма. Его площадь равна половине площади четырёхугольника, а его центр лежит на точке пересечения средних линий. Этот параллелограмм называется параллелограммом Вариньона;
- Последний пункт означает следующее: В выпуклом четырёхугольнике можно провести четыре средние линии второго рода. Средние линии второго рода — четыре отрезка внутри четырёхугольника, проходящие через середины его смежных сторон параллельно диагоналям. Четыре средние линии второго рода выпуклого четырёхугольника разрезают его на четыре треугольника и один центральный четырёхугольник. Этот центральный четырёхугольник является параллелограммом Вариньона.
- Точка пересечения средних линий четырёхугольника является их общей серединой и делит пополам отрезок, соединяющий середины диагоналей. Кроме того, она является центроидом вершин четырёхугольника.
- В произвольном четырёхугольнике вектор средней линии равен полусумме векторов оснований.
Средняя линия трапеции [ править | править код ]

Средняя линия трапеции — отрезок, соединяющий середины боковых сторон этой трапеции. Отрезок, соединяющий середины оснований трапеции, называют второй средней линией трапеции.
Она рассчитывается по формуле: E F = A D + B C 2 <displaystyle EF=<frac <2>>> 


07.06.2019 
5 июня Что порешать по физике
30 мая Решения вчерашних ЕГЭ по математике
Площадь треугольника ABC равна 176, DE — средняя линия. Найдите площадь треугольника CDE.
Средняя линия отсекает от треугольника подобный ему с коэффициентом подобия Площади подобных фигур относятся как квадрат коэффициента подобия. Тогда
Выясним, как связаны средняя линия треугольника и его площадь.
 I. Площадь треугольника равна половине произведения основания на высоту, проведённую к этой стороне:
I. Площадь треугольника равна половине произведения основания на высоту, проведённую к этой стороне:
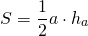
Поскольку средняя линия треугольника, соединяющая середины двух сторон, равна половине третьей стороны:
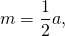
то можно найти площадь треугольника через его среднюю линию:
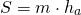
Площадь треугольника равна произведению средней линии и высоты, перпендикулярной этой средней линии.
II.Прямая, параллельная стороне треугольника и пересекающая две другие его стороны, отсекает от него подобный треугольник.
 Если MN- средняя линия треугольника ABC и MN параллельна AC, то треугольники ABC и MBN подобны.
Если MN- средняя линия треугольника ABC и MN параллельна AC, то треугольники ABC и MBN подобны.
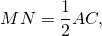
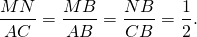
Так как площади подобных треугольников относятся как квадраты их соответствующих сторон, то
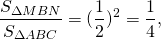
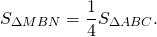
Средняя линия треугольника отсекает от него треугольник, площадь которого равна четверти площади исходного треугольника.
Например, если площадь треугольника ABC равна 40 см², то средняя линия MN, параллельная стороне AC, делит его площадь на части:
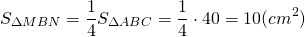
Площадь трапеции AMNC составляет три четверти площади треугольника ABC
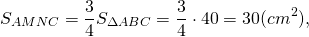
или может быть найденакак разность площадей треугольников ABC и MBC.
Как найти среднюю линию треугольника?

О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Понятие треугольника
Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, которые не лежат на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
- Прямоугольный. Один угол прямой, то есть равен 90 градусам, два других меньше 90 градусов.
- Остроугольный. Градусная мера всех углов больше 0, но меньше 90 градусов.
- Тупоугольный. Один угол тупой, два других — острые.
Треугольник считают равнобедренным, если две его стороны равны. Эти стороны называют боковыми сторонами, а третью — основанием.
Треугольник, у которого все стороны равны, называется равносторонним или правильным.
Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, которая лежит напротив прямого угла — гипотенуза, а две другие стороны — катеты.
Правильный (равносторонний или равноугольный) треугольник — это правильный многоугольник, в котором все стороны равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.
Свойства треугольников:
- В треугольнике против большего угла лежит большая сторона — и наоборот.
- Сумма углов треугольника равна 180 градусов.
- Все углы равностороннего треугольника равны 60 градусам.
- В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Понятие средней линии треугольника
Определение средней линии треугольника подходит для любого вида этой фигуры.
Средняя линия треугольника — отрезок, который соединяет середины двух сторон. В любом треугольнике можно провести три средних линии.
Основанием считается сторона, которой параллельна средняя линия.
Как найти среднюю линию треугольника — расскажем дальше, а для начала еще немного разберемся со всеми определениями.
Понятие средней линии прямоугольного треугольника
Математики говорят: в любом треугольнике можно провести три средних линии. В прямоугольном треугольнике этот отрезок будет равен половине основания — это и есть формула средней линии прямоугольного треугольника.
Прямой угол помогает нам применить другие признаки равенства и подобия. Для углов в прямоугольном треугольнике можно использовать геометрические тождества без дополнительных построений, а любую из сторон можно найти по теореме Пифагора.
В прямоугольном треугольнике две средние линии перпендикулярны катетам, а третья равна медиане, проведенной к гипотенузе. Средние линии острого и разностороннего треугольника не обладают подобными свойствами.
Свойства средней линии треугольника
Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.
Свойства:
- Средняя линия равна половине длины основания и параллельна ему.
- Средняя линия отсекает треугольник, подобный данному с коэффициентом 1/2; его площадь равна четверти площади данного.
- Три средние линии разделяют исходную фигуру на четыре равных треугольника. Центральный из них называют дополнительным.
- Три средние линии разделяют исходный прямоугольный треугольник на четыре равных прямоугольных треугольника.
Теорема о средней линии треугольника
Теорема о средней линии треугольника звучит так:
Средняя линия треугольника параллельна основанию и равна его половине. А так выглядит формула нахождения средней линии треугольника:
Докажем теорему:
По условию нам дано, что MA = MB, NA = NC
Рассмотрим два образовавшихся треугольника ΔAMN и ΔABC.
(по второму признаку подобия треугольников).
△ABC, то Следовательно, ВС = 2МN. Значит, доказано, что средняя линия равна половине основания.
△ABC, то ∠1 = ∠2 . Так как ∠1 и ∠2 — соответственные углы, то по признаку параллельности прямых MN || BC.
Параллельность средней линии и соответствующего ей основания доказана.
Пример 1. В треугольнике ΔABC AB = 8, BC = 7, CA = 5, точки M, K, N — середины сторон AB, BC, CA соответственно. Найти периметр ΔMNK.
Соединим середины сторон треугольника ΔABC и получим его средние линии, которые образуют треугольник ΔMNK. Найдем их длины по теореме о средней линии:
Ответ: периметр треугольника ΔMNK равен 10.
Пример 2. В прямоугольном треугольнике АВС есть две средние линии: MN и NP, равные 3 и 4 соответственно. Найти площадь большого прямоугольного треугольника.
Площадь треугольника равна половине произведения основания на высоту. Так как треугольник прямоугольный, то его площадь найдем как половину произведения катетов:
Так как MN — средняя линия, то по теореме о средней линии она равна половине катета AC:
Значит, AC = 2MN = 2 × 3 = 6.
Так как NP — средняя линия, то по теореме о средней линии она равна половине катета BC:
Значит, BC = 2NP = 2 × 4 = 8.
Тогда найдем площадь большого треугольника, используя формулу, указанную выше:
S = ½ × 6 × 8 = ½ × 48 = 24.
Ответ: площадь большого прямоугольного треугольника равна 24.
Средняя линия треугольника – свойства, признаки и формулы
Одним из важных понятий, с помощью которого легко решается целый класс задач по геометрии, является средняя линия треугольника.
Разберём данное понятие, рассмотрим свойства, и научимся правильно решать задачи на эту тему.
Определение и признаки средней линии треугольника
Отрезок, соединяющий середины двух сторон треугольника, называется его средней линией.
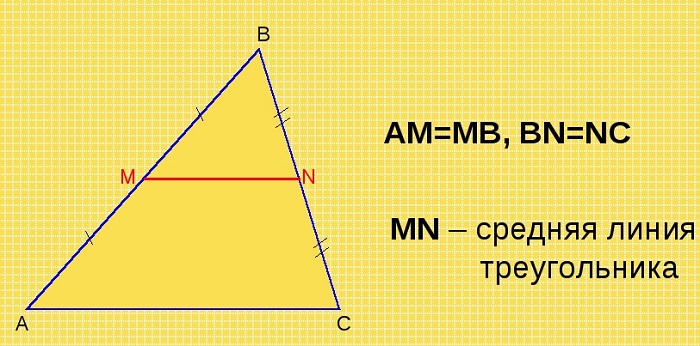
Отрезок, у которого один из концов совпадает с серединой одной из сторон, другой находится на второй стороне, проведённый параллельно третьей стороне, является средней линией треугольника.
Доказательство следует из теоремы Фалеса.

Теорема о средней линии треугольника
Средняя линия треугольника параллельна основанию (третьей стороне) и равна её половине.
Существует три вида доказательств этого положения. Каждое из них базируется на одной из ключевых позиций планиметрии.
Пусть дан треугольник ABC, M – середина стороны AB, N – середина BC.
По определению, MN – средняя линия ΔABC.
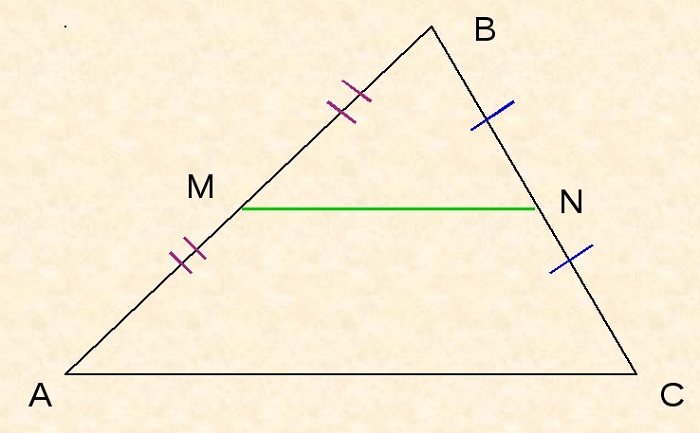
Необходимо доказать, что MN II AC, MN = ½AC.
Доказательства
Пусть прямая MK II AC. Тогда по теореме Фалеса MK пересекает сторону BC в её середине. В этом случае отрезок MN лежит на прямой MK.
Следовательно, MN II AC.
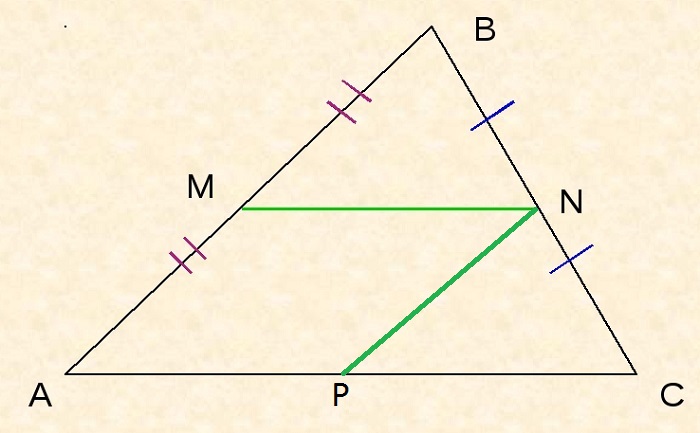
Тогда NP – средняя линия по теореме Фалеса, то есть AP = PC.
Так как AMNP – параллелограмм по определению, то AP = MN. Из этого и предыдущего утверждения следует, что длина MN равна ½AC.
Рассматриваются треугольники MBN и ABC. В них угол B является общим,
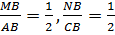
По второму признаку подобия треугольников ΔMBN ∼ ΔABC. Следовательно, углы BMN и BAC равны.
Поскольку эти углы являются соответственными, то прямые MN и AC параллельны.
Формула MN = ½AC следует из условий
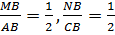
поскольку пропорциональность двух пар сторон влечёт соответствующее отношение для третьей пары сторон.
Рассматривается сумма векторов
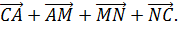
Поскольку в результате образуется замкнутая ломаная, то
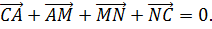
Отсюда следует, что
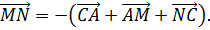
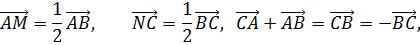
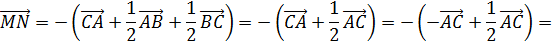
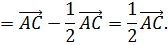
Из последнего равенства следуют условия теоремы.
Следствия из теоремы с доказательствами
Следствие №1
Средняя линия отсекает треугольник, подобный данному, с коэффициентом подобия ½ и площадью, составляющий ¼ площади заданного треугольника.

По определению стороны AB и BC делятся пополам, поэтому
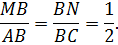
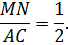
Из третьего признака подобия вытекает рассматриваемое свойство.
Поскольку площади подобных фигур относятся как квадрат коэффициента подобия, то получается вторая часть свойства, то есть площадь маленького треугольника относится к площади большого как
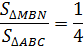
Следствие №2
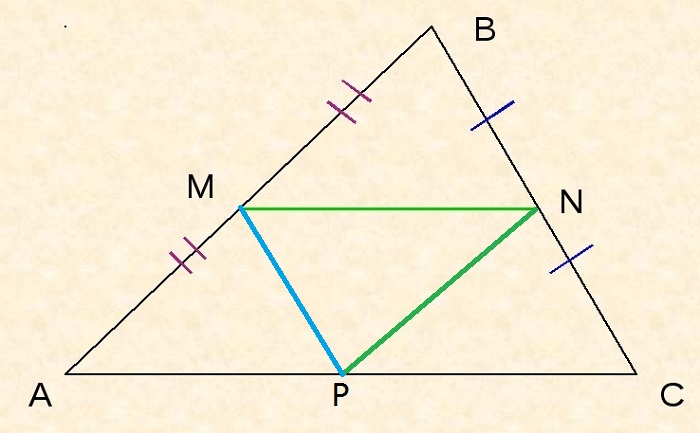
Поскольку MN – средняя линия, то MN II AC, поэтому ∠BMN = ∠BAP, ∠BNM = ∠BCA как соответственные при MN II AC и секущей AB или BC соответственно.
Поскольку MP – средняя линия, то MP II BC, поэтому ∠MPA = ∠BCA как соответственные при MP II BC и секущей AC.
Таким образом: ∠BNM = ∠BCA = ∠MPA.
Так как MN – средняя линия, то сторона MN = ½AC, поэтому MN = AP.
Следовательно, ΔAMP = ΔMBN по второму признаку равенства треугольников.
Равенство остальных пар треугольников доказывается аналогично.
По основному свойству ΔMBN ∼ ΔABC с коэффициентом подобия ½. Так как все полученные маленькие треугольники равны между собой, то каждый из них, следовательно, подобен большому с тем же коэффициентом.
Свойства средней линии треугольника
Теорема и следствия из неё составляют основные свойства средней линии треугольника.
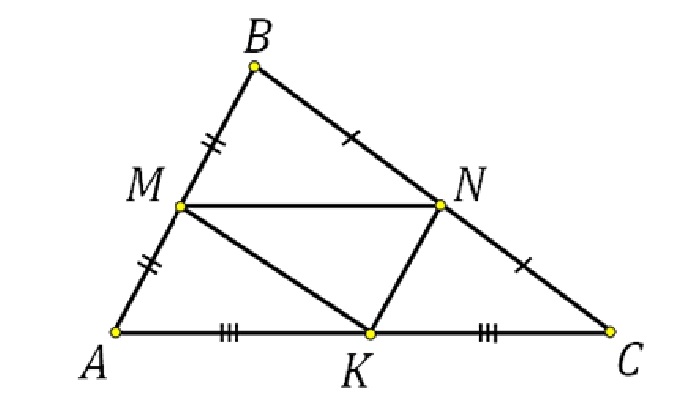
Согласно второму утверждению, вид большого треугольника такой же, как и у маленьких. То есть для равностороннего и равнобедренного треугольников средние линии отсекают равносторонние и равнобедренные треугольники.
Высоты тупоугольного треугольника, проведённые к тупому углу из вершин острых, располагаются вне треугольника. Поэтому часто рассматривают не саму среднюю линию, а её продолжение. Учитывая подобие получаемых фигур, можно утверждать, что точкой пересечения с продолжением средней линии высота делится на две равные части.
Биссектриса угла треугольника точкой пересечения со средней линией также делится пополам.
Средняя линия прямоугольного треугольника
Для прямоугольного треугольника две средние линии перпендикулярны катетам, а третья равна медиане, проведённой к гипотенузе.
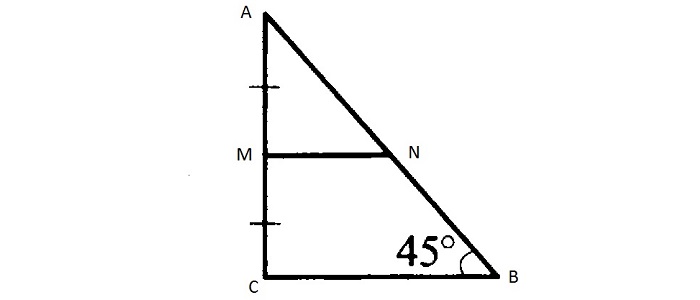
Остроугольный разносторонний треугольник не имеет средних линий, обладающих подобными характеристиками.
Пример решения задачи
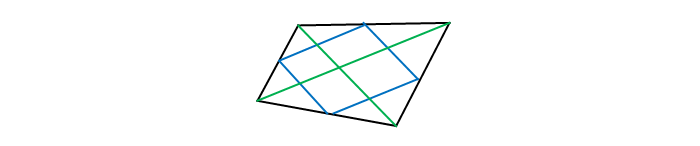
Доказать, что середины сторон произвольного выпуклого четырёхугольника являются вершинами параллелограмма.
Проводя диагональ четырёхугольника, получают разбиение на два треугольника, в каждом из которых построена средняя линия, параллельная по основной теореме диагонали, как основанию.
Так как две прямые, параллельные третьей, параллельны между собой, то противолежащие стороны образованного средними линиями четырёхугольника параллельны.
Аналогично доказывается параллельность двух других сторон нового четырёхугольника. По определению четырёхугольник, полученный соединением середин сторон заданного четырёхугольника, является параллелограммом.
Треугольник, образованный средними линиями равнобедренного треугольника, называется : а) прямоугольным б) равносторонним помогите пож?
Геометрия | 5 – 9 классы
Треугольник, образованный средними линиями равнобедренного треугольника, называется : а) прямоугольным б) равносторонним помогите пож.

Он не может называться ни равносторонним ни прямоугольным, так как две средние линии равны половине боковых (равных) сторон, а третья равна половине основания – этот треугольник будет равнобедренным.
Если угол при вершине равен 90 градусов, то он будет еще и прямоугольным, но об углах ничего не сказано.
Ответ, оба варианта неверны.

Люди, пожалуйста помогите?
Люди, пожалуйста помогите!
Прямоугольная трапеция диагональю разделена на 2 треугольника.
Один из них равносторонний треугольник со стороной а, а второй – прямоугольный треугольник.
Найдите среднюю линию трапеции.

Площадь равностороннего треугольника ABC равна 60см в квадрате?
Площадь равностороннего треугольника ABC равна 60см в квадрате.
Найдите площадь треугольника, образованного средними линиями треугольника ABC.

Прямоугольная трапеция разделяется диагональю на два треугольника – равносторонний со стороной а и прямоугольный?
Прямоугольная трапеция разделяется диагональю на два треугольника – равносторонний со стороной а и прямоугольный.
Найдите среднюю линию трапеции.

Средняя линия отсекает от данного треугольника равнобедренный прямоугольный треугольник?
Средняя линия отсекает от данного треугольника равнобедренный прямоугольный треугольник.
Найдите углы данного треугольника.

Треугольник образованный средними линиями прямоугольного треугольника является каким?
Треугольник образованный средними линиями прямоугольного треугольника является каким?

Площадь равностороннего треугольника АВС равна 60 см?
Площадь равностороннего треугольника АВС равна 60 см.
Найдите площадь треугольника , образованного средними линиями треугольника АВС.

Помогите решить?
Прямоугольная трапеция делится диагональю на два треугольника – – равносторонний со стороной а и прямоугольный.
Найдите среднюю линию трапеции.

Периметр равностороннего треугольника равен 45 см?
Периметр равностороннего треугольника равен 45 см.
Найдите периметр треугольника, который образован средними линиями заданного треугольника.

Прямоугольная трапеция делится диагональю на прямоугольный и равнобедренный треугольники?
Прямоугольная трапеция делится диагональю на прямоугольный и равнобедренный треугольники.
Найдите среднюю линию трапеции, если периметр равностороннего треугольника равен 27дм помогите пожалуйста с решением ответ должен получиться6.
75дм можно с чертежом.

Треугольник образован средними линиями равнобедренного треугольника является ?
Треугольник образован средними линиями равнобедренного треугольника является :
Вопрос Треугольник, образованный средними линиями равнобедренного треугольника, называется : а) прямоугольным б) равносторонним помогите пож?, расположенный на этой странице сайта, относится к категории Геометрия и соответствует программе для 5 – 9 классов. Если ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему. Для этого ключевые фразы введите в строку поиска, нажав на кнопку, расположенную вверху страницы. Воспользуйтесь также подсказками посетителей, оставившими комментарии под вопросом.

Угол 2 = 180 – 130 = 50 Углы два и три вертикальных следовательно угол 2 равен углу 3 Угол 4 90 – 50 = 40 Ответ : 1угол – 50градусов 2угол – 50градусов 3угол – 40градусов.

1. Найдем координатыАС = (2 + 3 ; – 1 + 1) = (5 ; 0) ВD = ( – 2 + ( – 1) ; – 4 + 1) = ( – 3 ; – 3) ; AC = [tex] sqrt < (2 – 3) ^ <2>+ ( – 1 – 1 ) ^ <2>> = sqrt <5>; BD = [tex] sqrt < ( – 2 + 1 ) ^ <2>+ x( – 4 – 4) ^ <2>> = sqrt <65>; 2) коо..

P = 2(AB + BC) AB = x + 8 BC = x P = 104 104 = x + x + 8 X = 22 BC = 22 AB = 22 + 8 = 30.

По теореме пифагора √169 – 25 = √144 = 12.

Можно решить и по теореме Пифагора.

Точки А, В, С не могут лежать на одной прямой.

Треугольники подобныпо двум сторонам и углу между ними следовательно A1C1 в 4 раза меньше. A1C1 = 30 / 4 = 7. 5 м.

ПЛОЩАДЬ ТРАПЕЦИИ = полусумма длин оснований * на высотув трапеции проводим высоту СН, рассмотрим треугольник СДНуголД = 45 градусовугол Н = 90 градусовиз этого следует, что уголС = 45 градусов, а из этого следует треугольник СДН – равнобедренныйСН = ..

Внешний угол треугольника равен сумме двух других углов (не смежных с ним) , АВ = ВС, значит угол А равен углу С, получаем С = 70 / 40 = 1. 75.

Гипотенуза АВ по т. Пифагора равна BC = корень(AB ^ 2 + AC ^ 2) = корень(10 ^ 2 + 6 ^ 2) = корень(136) = 2 * корень(34)По определению синуса острого угла прямоугольного треугольникаsin B = AC ABsin B = 10 (2 * корень(34)) = 5 (корень(34))ответ..
[spoiler title=”источники:”]
http://nauka.club/matematika/geometriya/srednyaya-liniya-treugolnika.html
http://geometria.my-dict.ru/q/2807256_treugolnik-obrazovannyj-srednimi-liniami-ravnobedrennogo-treugolnika/
[/spoiler]
Рассмотрим задачу на подобие, где требуется найти площадь треугольника, средняя линия которого делит его на части.
Утверждение.
Средняя линия треугольника делит его на треугольник и трапецию, площади которых относятся как 1:3.
 Дано: ∆ ABC,
Дано: ∆ ABC,
FK — средняя линия
Доказать:
![]()
Доказательство:

Рассмотрим ∆ FCK и ∆ ACB
По свойству средней линии треугольника, FK∥AB и FK=1/2 AB.
Отсюда, ∠CFK=∠CAB (как соответственные при FK∥AB и секущей AC).
∠C — общий.
Следовательно, ∆ FCK и ∆ ACB подобны (по двум углам).
Так как площади подобных фигур относятся как квадраты их соответствующих линейных размеров, то
![]()
Таким образом,
![]()
а так как
![]()
Итак, средняя линия треугольника делит его на треугольник и трапецию, площади которых, соответственно, составляют одну четверть и три четверти от площади исходного треугольника, значит,
![]()
Что и требовалось доказать.
Задача.
 Дано:
Дано:
∆ ABC,
F — середина AC,
K — середина BC,
![]()
Найти:
![]()
Решение:
Пусть
![]()
По доказанному выше утверждению,
![]()
Значит,
![]()
Поскольку
![]()
![]()
![]()
![]()
Ответ: 18 см².
Применение подобия к доказательству теорем и решению задач. Средняя линия треугольника и трапеции
Разделы:
Математика
Цели урока:
- ввести определение средней линии треугольника,
трапеции; - сформулировать и доказать теорему о средней
линии треугольника; - рассмотреть решение задач на применение этой
теоремы; - пропедевтика свойства средней линии трапеции.
Ход урока
I. Организационный момент
II. Устная работа
III. Объяснение нового материала
IV. Закрепление изученного материала
V. Итоги урока
VI. Домашнее задание.
I. Оргмомент. Учитель сообщает тему урока.
II. Устно (фронтальная работа с классом).
1. Какие треугольники называются подобными?
2. Являются ли треугольники (рис. 1) подобными? На
основании какого признака подобия?
3. Что можно сказать об углах этих
треугольников?
4. Какие признаки подобия треугольников вы еще
знаете?
Эти факты будем использовать при решении задач.
5. Во сколько раз АВ больше МВ, а ВС больше ВN? (по
рис. 2)
Что можно сказать о АВС и МВN?
(рис. 2). На основании какого признака подобия?
7. Сравните площади этих треугольников?
Сделаем запись:
Имеем
Записываем в тетрадь тему урока.
III. Объяснение нового материала
- Дать определение средней линии треугольника.
- Сформулировать теорему о средней линии
треугольника (предложить учащимся
самостоятельно сформулировать теорему, опираясь
на 9 вопрос устных упр
IV. Закрепление изученного материала
Закрепление изученного материала
1. Чему равны средние линии треугольника со
сторонами 14 см, 16 см, 20 см? Использовать модель
(вырезать из цветной бумаги, заранее отметить
середины сторон). Перегибая ?, обсудить с
учащимися ответы.
2. №564 у.
Дан треугольник, стороны которого равны 8 см, 5
см, 7 см. Найдите периметр треугольника, вершинами
которого являются середины сторон данного
треугольника.
Сделать вывод про периметр и площадь этого
треугольника.
3. № 567 (письм)
Докажите, что середины сторон произвольного
четырехугольника являются вершинами
параллелограмма.
Вопрос классу: Как доказать, что
четырехугольник является параллелограммом?
(Надо использовать признаки параллелограмма)
Из того, что M, N – середины сторон АВ и ВС, что
можно сказать об отрезке MN?
Записываем в тетрадях решение:
Из п.1 и п.2
PM = 1/2 AD; MK = 1/2 BC
PK = 1/2 (AD + BC)
Как вы думаете, как называется отрезок,
соединяющий боковые стороны трапеции? Чему он
равен? [Этот отрезок равен полусумме оснований].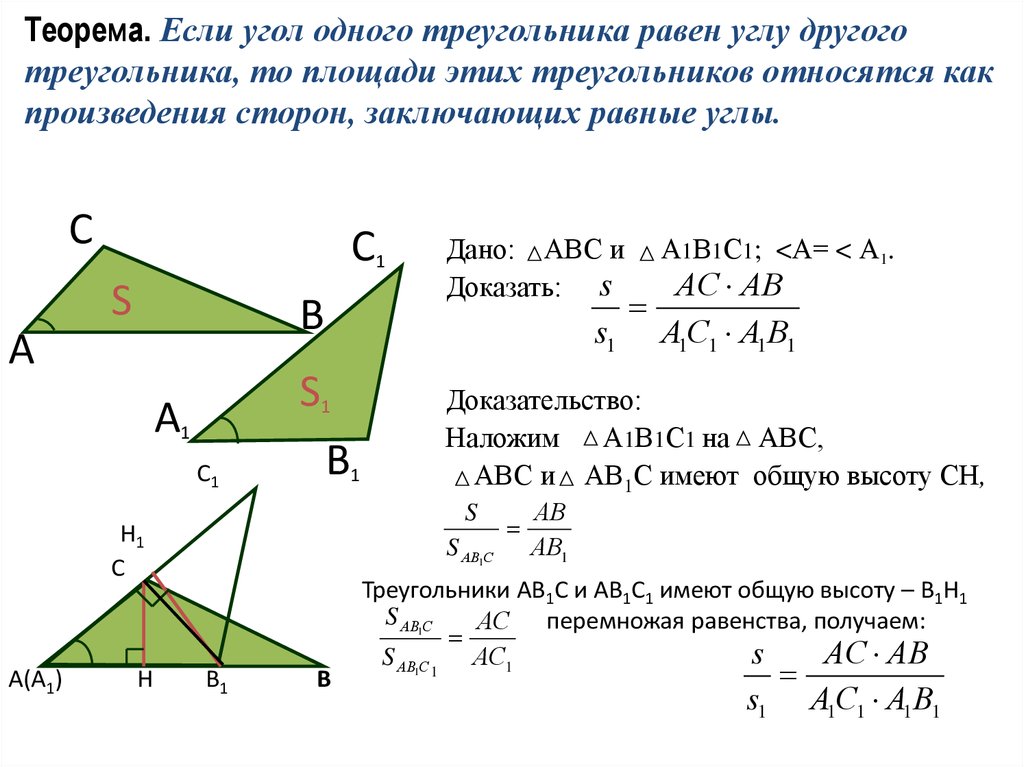
V. Подводим итоги урока
1. Возьмите белый лист (приложение 1)
и выполните задание.
2. Устно (по заранее заготовленному чертежу)
решение задачи
Повторить выводы, сделанные на уроке:
1) периметр треугольника, образованного
средними линиями данного треугольника, вдвое
меньше периметра данного треугольника;
2) площадь треугольника, образованного средними
линиями данного треугольника, вчетверо меньше
площади данного треугольника;
3) средние линии разбивают треугольник на
четыре треугольника равной площади.
Домашнее задание.
Вопр.8 стр. 154 № 565; 566; 568(а).
Замечание:
Приложение 2 использовать как
дополнение, если позволяет время.
Литература:
- Геометрия. Учебник для 7-9 кл. об/об учр. (Л.С.
Атанасян и др.), М., Просвещение, 2000; - Рабинович Е.М. Задачи и упражнения на готовых
чертежах 7-9 кл., М., Илекса, 2006; - Левитас Г.Г. Карточки для коррекции знаний по
геометрии для 8-9 кл.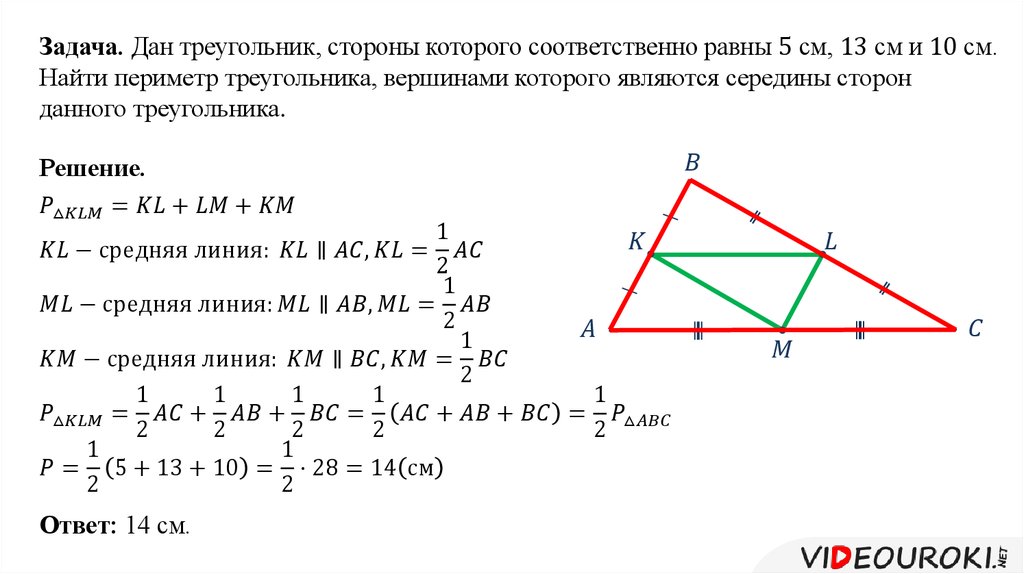 М., Илекса, 2003;
М., Илекса, 2003; - Шуба М.Ю. Занимательные задания в обучении
математике, М.: Просвещение, 1994.
12.03.2008
Средняя линия треугольника | План-конспект урока по геометрии (8 класс) по теме:
Методическая разработка урока математики в 8 классе.
Тема урока «Средняя линия треугольника».
Тип урока: урок усвоения новых знаний
Цели урока:
Образовательные:
- Ввести понятие средней линии треугольника; доказать свойство средней линии треугольника, а также теорему о пересечении медиан треугольника; рассмотреть свойства медианы и средней линии треугольника применительно к его площади; научить применять их при решении задач.
Развивающие:
- Развивать интерес с к геометрии, логическое мышление, интуицию учащихся; формировать умения чётко и ясно излагать свои мысли;
совершенствовать графическую культуру.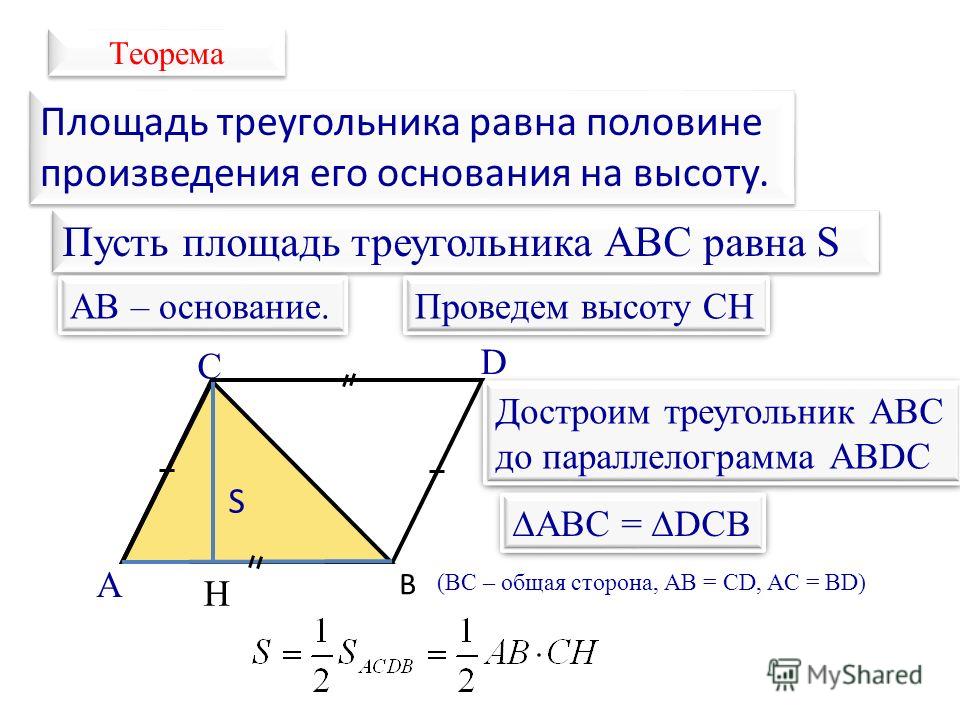
- Развивать творческую и мыслительную деятельность учащихся, их интеллектуальные качества: способность к исследовательской деятельности, к синтезу и анализу.
Воспитательные:
- Мотивировать детей к самообразованию.
- Воспитывать интерес к геометрии, расширять кругозор учащихся
- Прививать аккуратность в оформлении геометрических задач, культуру устной речи.
Оборудование, наглядность, электронные приложения к уроку:
Компьютер. Мультимедийный проектор. Документ камера.
Презентация Microsoft PowerPoint.
Структура урока.
|
Вид деятельности. |
№ слайдов. |
мин. |
|
1. Постановка цели урока. Эпиграф к уроку. |
1-3 |
2 |
|
2. Проверка домашнего задания |
2 |
|
|
3. Повторение изученного материала. |
4-6 |
3 |
|
4. Понятие средней линии треугольника и её свойство. Математический диктант |
7-9 10-14 |
12 |
|
5. Физкультминутка. |
1 |
|
|
6. Свойство медиан треугольника. Следствия. |
15-17 18-21 |
15 |
|
7. Закрепление нового материала. Решение задач. |
22-23 |
8 |
|
8. Подведение итогов. |
24 |
2 |
|
9. Домашнее задание. |
25 |
1 |
Ход урока.
1. Вступительное слово учителя.
Эпиграфом к сегодняшнему уроку взяты слова французского писателя XIX столетия. Анатоль Франс однажды заметил: “Учиться можно только весело… Чтобы переваривать знания, надо поглощать их с аппетитом” (сайд №2).
Давайте последуем совету писателя и на сегодняшнем уроке: будьте активны, внимательны, поглощайте с большим желанием знания, которые пригодятся вам в дальнейшей жизни.
Многие известные мыслители и писатели прошлого обращались к темам о замечательных точках и линиях треугольника. Сегодня мы тоже займемся этим интересным исследованием.
Тема нашего урока «Средняя линия треугольника». Давайте сформулируем, какие цели мы должны достичь: (учащиеся самостоятельно формулируют цели, слайд №3)
- Дать определение средней линии треугольника.
- Доказать теорему о средней линии треугольника.
- Доказать теорему о пересечении медиан треугольника.
2. Проверка домашнего задания.
С помощью документ камеры решение домашнего задания (№ 568 б) из тетради учащегося проектируется на экран. Учащийся комментирует решение.
3. Устная работа. Повторение изученного материала.
Цель: систематизировать базовые знания по теме «Подобие треугольников»; развивать логическое мышление; формировать умение четко и ясно излагать свои мысли.
Чтобы успешно выполнить цели сегодняшнего урока, нам не раз придется обращаться к признакам подобия треугольников. Какие признаки подобия треугольников вы знаете? Учащиеся формулируют признаки подобия треугольников (слайд 4-6).
4. Понятие средней линии треугольника и ее свойства.
Цели: сформулировать определение средней линии треугольника и доказать ее свойство; развивать умение сравнивать и анализировать.
— Что общего у треугольников, изображенных на рисунке? (слайд №7)
Учащиеся самостоятельно дают определение средней линии треугольника(слайд №8).
— Сколько средних линий можно построить в треугольнике?
-Средняя линия треугольника — это замечательная линия треугольника. А чем же она замечательна? Давайте сформулируем и докажем свойство средней линии треугольника (слайд №9).
Теорему учащиеся доказывают самостоятельно (задание получено сильным учащимся предварительно). С целью закрепления понятия и свойства средней линии треугольника проводится математический диктант (решение задач по готовым чертежам; слайд № 10-14).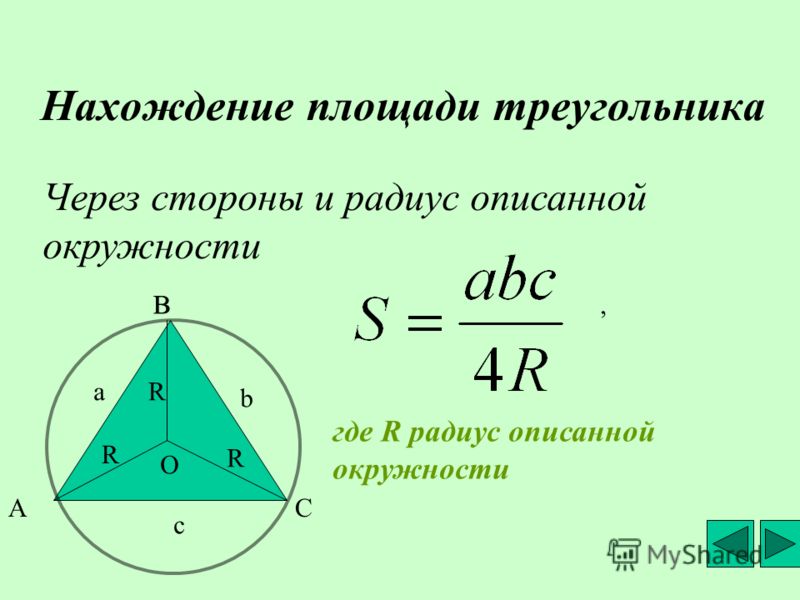 Учащиеся получают карточки, выполняют математический диктант.
Учащиеся получают карточки, выполняют математический диктант.
Математический диктант
|
Вариант 1 |
Вариант 2 |
|
1)Две стороны треугольника соединили отрезком, непараллельным третьей стороне. Является ли этот отрезок средней линией данного треугольника? |
1)Точки А и В являются серединами двух сторон треугольника. Как называется отрезок АВ? |
|
2)В ∆АВС сторона АВ=7 см. Чему равна средняя линия треугольника, параллельная этой стороне? |
2)Средняя линия треугольника АВD, параллельная стороне ВD, равна 4 см. Чему равна сторона ВD? |
|
3) Дано: МК=3, KN=4, MN=5. Найти периметр треугольника АВС. |
3) Дано: АВ=3м, ВС=5м, АС=4м. Найти периметр треугольника MNK. |
|
4) Концы отрезка АВ лежат на сторонах треугольника, а его длина равна половине третьей стороны. Обязательно ли: АВ – средняя линия этого треугольника? |
4)Концы отрезка MN лежат на сторонах треугольника. Обязательно ли: MN – средняя линия этого треугольника? |
|
5) Периметр треугольника равен 5,9 см. Найти периметр треугольника, отсекаемого одной из его средних линий. |
5)Периметр треугольника равен 7,3 см. Найти периметр треугольника, отсекаемого одной из его средних линий. |
5. Физкультминутка
6. Свойство медиан треугольника
Цель: развивать логическое мышление; способность к исследовательской деятельности, к синтезу и анализу.
Вспомните, что называется медианой треугольника? (слайд №15) Укажите рисунок, на котором изображена медиана.
Свойство медиан треугольника: медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины (слайд № 16).
Теорему учащиеся доказывают самостоятельно (задание получено сильным учащимся предварительно).
-Медиану тоже считают замечательной линией треугольника. Как вы считаете, почему? Вспомните, какие треугольники называются равновеликими (слайд 17)?Давайте, исследуем следующие предположения. В треугольнике провели медиану. Как изменится площадь? (слайд № 18)
Как вы считаете, почему? Вспомните, какие треугольники называются равновеликими (слайд 17)?Давайте, исследуем следующие предположения. В треугольнике провели медиану. Как изменится площадь? (слайд № 18)
|
Утверждение: медиана треугольника делит его на два равновеликих треугольника. |
-В параллелограмме, площадь которого равна S, проведены диагонали. Чему равны площади образовавшихся треугольников (слайд №19)?
Следствие 1: диагонали параллелограмма делят его на четыре равновеликих треугольника.
— В треугольнике проведены три медианы. Являются ли они равновеликими (слайд № 20)?
Следствие 2: медианы треугольника делят его на шесть равновеликих треугольников.
— В треугольнике проведены средние линии. Чему равна площадь треугольника BMN (слайд № 21)?
Следствие 3: средняя линия треугольника отсекает от данного треугольник, площадь которого равна ¼ площади исходного треугольника.
7. Закрепление нового материала. Решение задач
Цель: научить учащихся применять приобретенные на уроке знания при решении задач; развивать логическое мышление; прививать аккуратность в оформлении геометрических задач; совершенствовать графическую культуру.
Задача 1. Медианы ВК и ЕМ, треугольника ВСЕ, пересекаются в точке О. Найти SMOK:SCMK (слайд №22).
Задача 2. Решите задачу устно по готовому чертежу (слайд № 23).
|
АА1, ВВ1, СС1 – медианы треугольника. Доказать:
|
8. Подведение итогов
Рефлексия.
- Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника.
- Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
- Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2 : 1, считая от вершины.
- Средняя линия треугольника отсекает от данного треугольник, площадь которого равна ¼ площади исходного.
- Три средние линии треугольника разбивают его на 4 равоновеликих треугольника, площадь каждого из них равна ¼ площади исходного.
Оценки за урок.
9. Домашнее задание
П. 62, вопросы 8, 9 (стр. 160). Задачи № 616, 571.
Литература
- Геометрия: Учеб. для 7-9 кл. общеобразоват. учреждений. / Л.С. Атанасян, В.Ф Бутузов, С.Б. Кадомцев и др. – 5-е изд. – М.: Просвещение, 1995. – 335 с.: ил. – ISBN 5-09-006554-3
- Лысенко Ф. Ф. Математика. Подготовка к ЕГЭ. – Ростов – на –Дону: «Легион М», 2012.
- Алтынов П.И. Геометрия. Тесты. 7-9 кл.
- Гилярова М. Г. Поурочные разработки по геометрии: 8 класс. Волгоград: « Учитель — АСТ», 2003.
- Интернет-сайты:
Интернет-государство учителей в разделе Инфотека-Математика.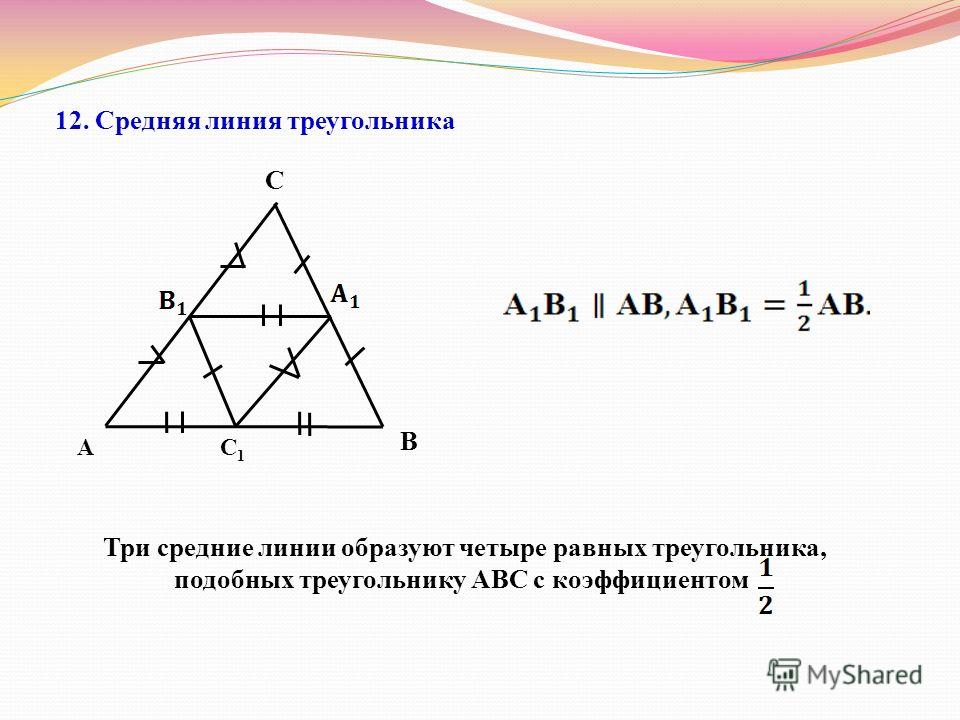 http://www.intergu.ru/infoteka/
http://www.intergu.ru/infoteka/
http://school-collection.edu.ru/
Упражнения для глаз: comp-doctor.ru/eye/eye_upr.php
подобных треугольников Теорема о средней линии треугольника
Теорема о средней линии треугольника . ТМТ. Звучит весело, да?
Хотя TMT и не так скандален, как TMZ, он делится множеством пикантных слухов о длине различных сегментов линий в мире треугольников и во всем мире. В частности, в нем говорится, что если вы соедините середины двух сторон треугольника, то вы получите срединный сегмент , волшебное существо, которое живет прямо в середине треугольника, который он называет своим домом. Средние сегменты составляют половину длины стороны, которой они идут параллельно, они делят две другие стороны пополам и пукают блестками. Нет, подождите, это единороги.
Здесь B — это середина AC , а D — это середина CE . Мы можем быть в этом уверены, потому что нам сказали, что отрезки конгруэнтны по обе стороны от обеих этих точек.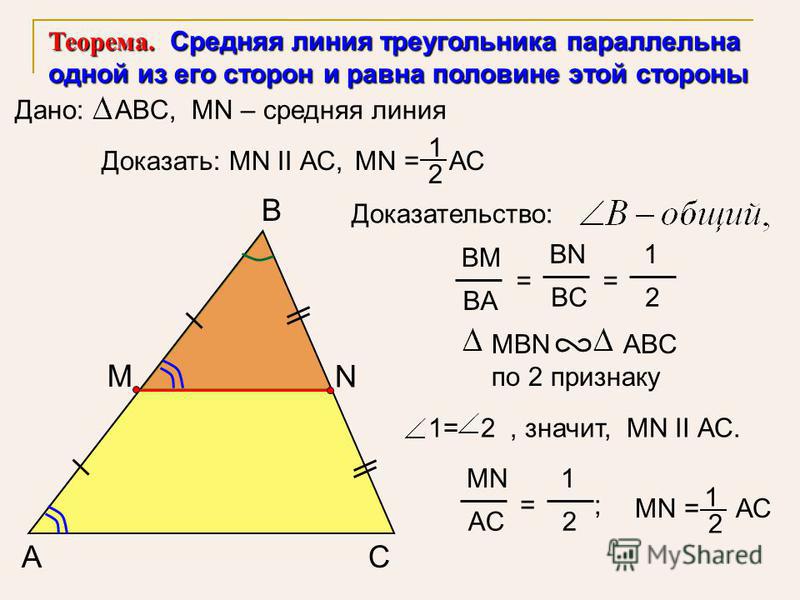 Соединив их, мы получим средний сегмент BD . TMT говорит, что BD || AE и что BD = × AE .
Соединив их, мы получим средний сегмент BD . TMT говорит, что BD || AE и что BD = × AE .
Пример задачи
Если GI = 11, какова длина FJ ?
Итак, мы видим, что GI является средним отрезком, так как FG ≅ GH , JI ≅ IH , и IH | 3 | ГИ . Это означает, что FJ дважды равно GI , поэтому FJ = 2 × 11 = 22. секущей, и они образуют конгруэнтные отрезки на одной из этих секущей, то отрезки на другой секущей также конгруэнтны. В Triangle Land (разве это не забавный тематический парк?) это говорит нам о том, что если у нас есть линия, параллельная одной стороне, которая пересекает вторую сторону в ее середине, то она автоматически пересекает и третью сторону в ее середине. .
(Да, мы сказали три параллельные линии. Третья параллельная линия проходит через вершину, противоположную первой стороне. Она невидима, как воображаемый друг вашего младшего брата, Космический рейнджер Бастер.)
Она невидима, как воображаемый друг вашего младшего брата, Космический рейнджер Бастер.)
Итак, если мы посмотрим снова в ∆ FJH , где нам дано, что G является средней точкой FH и FJ || GI , тогда мы можем понять, что I является средней точкой JH . Спасибо, ТМТ.
Пример задачи
∆ VXY имеет срединный сегмент WZ , где W — середина VX . Если VX = 14 и VZ = 4, то какой длины будут VW и VY ?
Поскольку WZ является средним сегментом, мы знаем, что он делит VX и VY пополам, вот так: VW = 7. А потому что VZ = 4, VY = 8.
Но мы можем сделать еще один шаг вперед. Это следствие работает не только для конгруэнтных сегментов, но и для любых пропорциональных сегментов. Да, больше пропорций. Пожалуйста, не ненавидьте нас.
Параллельные прямые, пересекающие трансверсали, создают пропорциональные сегменты на этих трансверсалях.
В ∆ ADE мы можем установить следующие пропорции, чтобы найти недостающие длины: . Разберемся с каждым из них отдельно.
Перемножьте, чтобы получить 4 × GF = 15. Разделите обе части на 4, и мы найдем GF = 3,75.
Снова перекрестное умножение, и мы получаем 4 × AG = 40. Разделим обе части на 4 (ух ты, дежа вю) и на этот раз мы получим AG = 10.
Пример задачи
Найдите решение значения a и b .
Благодаря ТМТ и ее следствиям мы можем установить пропорции, чтобы найти недостающие длины.
7 A = 20
A = 2,857142
4 B = 42
B = 10,5
. . Этот урок даст координатное доказательство теоремы о середине треугольника. Что такое теорема о средней линии треугольника?
Если отрезок соединяет середины сторон треугольника, то этот отрезок параллелен третьей стороне и равен половине длины третьей стороны.
Вот доказательство теоремы о середине треугольника
Доказательство теоремы.
Рассмотрим следующий треугольник в системе координат.
|
Дано: S — середина OQ R — середина PQ Докажите: СР = ОП |
|
Дано:
S — середина OQ R — середина PQ Докажите: СР = ОП |
Чтобы доказать, что SR || ОП, мы можем просто показать, что их наклоны равны.
|
С: ( б + 0 , |
с + 0 ) |
«=» б , |
с ) |
|
С: ( б + 0 , |
с + 0 ) |
«=» б , |
с ) |
|
Р: ( а + б , |
с + 0 ) |
«=» а + б , |
с ) |
|
Р: ( а + б , |
с + 0 ) |
«=» а + б , |
с ) |
Поскольку координата y одинакова для обеих точек, наклон SR равен нулю.
 Признаки подобия треугольников.
Признаки подобия треугольников. Отрезок MN параллелен третьей стороне и равен его четверти.
Отрезок MN параллелен третьей стороне и равен его четверти.