Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Сторона треугольника равна 10, а проведённая к этой стороне высота равна 5. Найдите площадь треугольника.
2
В треугольнике одна из сторон равна 10, другая равна а угол между ними равен 60°. Найдите площадь треугольника.
3
Найдите площадь треугольника, изображённого на рисунке.
4
В треугольнике ABC отрезок DE — средняя линия. Площадь треугольника CDE равна 97. Найдите площадь треугольника ABC.
5
На стороне AC треугольника ABC отмечена точка D так, что AD = 3, DC = 7. Площадь треугольника ABC равна 20. Найдите площадь треугольника BCD.
Источник: Банк заданий ФИПИ
Пройти тестирование по этим заданиям
Здравствуйте, уважаемые читатели. В этой статье рассмотрим задачи по геометрии за 8-9 класс. Задачи на нахождение площади треугольника. Они встречаются в 15 задании ОГЭ по математике.
В статье будут рассмотрены несколько формул вычисления площади треугольника.
Первая теорема
Площадь треугольника равна половине произведения его высоты на сторону, к которой она проведена.
Задача №1
Сторона треугольника равна 16, а высота, проведённая к этой стороне, равна 19. Найдите площадь этого треугольника
Решение
Задача №2
У треугольника со сторонами 2 и 10 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 5. Чему равна высота, проведённая ко второй стороне?
Решение
Площадь треугольника равна половине произведения его высоты на сторону, к которой она проведена. Поэтому площадь треугольника в каждом случае будет одинаковой.
Задача №3
На стороне AC треугольника ABC отмечена точка D так, что AD=6, DC=10. Площадь треугольника ABC равна 48. Найдите площадь треугольника BCD.
Решение
Если на стороне треугольника взята точка, которая делит эту сторону в отношении m:n, то отрезок, соединяющий эту точку с вершиной противолежащего угла, делит треугольник на два треугольника, площади которых относятся как m:n:
Отрезок AD относиться к отрезку DC как 6:10. Значить площадь треугольника ABD составляет 6 частей от площади треугольника АВС, а площадь треугольника DBC – 10 частей. Вся площадь треугольника ABC равна 16 частей. По условию площадь треугольника АВС равна 48. Значит площадь треугольника ВСD=(48/16)*10=30.
Ответ 30
Задача №4
Два катета прямоугольного треугольника равны 4 и 10. Найдите площадь этого треугольника.
Решение
Вторая теорема
Площадь прямоугольного треугольника равна половине произведения его катетов.
Ответ 20
Задача №5
В прямоугольном треугольнике один из катетов равен 4, а угол, лежащий напротив него равен 45°. Найдите площадь треугольника
Решение:
Если в прямоугольном треугольнике, один из острых углов равен 45 градусам, то и второй острый угол равен 45 градусам, так как сумма острых углов в прямоугольном треугольнике равна 90 градусов. Если в треугольнике два угла равны, то этот треугольник равнобедренный.
Значит в треугольнике катеты равны 4 ( a=b=4). Найдем площадь равнобедренного прямоугольного треугольника:
Ответ 8
Задача №6
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 8 и 17.
Решение
Вспомним что такое катет и гипотенуза.
Стороны прямоугольного треугольника, которые образуют прямой угол, называются катеты, а третья сторона – гипотенуза.
Чтобы вычислить площадь прямоугольного треугольника, необходимо вычислить второй катет. Для этого воспользуемся теоремой Пифагора.
Теорема Пифагора
Квадрат гипотенузы равен сумме квадратов катетов.
Зная оба катета прямоугольного треугольника, вычислим его площадь:
Ответ 60
Задача №7
Катеты прямоугольного треугольника равны 21 и 72. Найдите высоту, проведенную к гипотенузе.
Решение
В этой задаче, чтобы найти высоту, проведенную к гипотенузе, необходимо воспользоваться двумя формулами нахождения площади треугольника. Первая формула (для прямоугольного треугольника): половина произведения его катетов. Вторая формула: половина произведения высоты на сторону, к которой эта высота проведена. Площадь, вычисленная разными формулами одной фигуры, одинаковая. Для решения, нам понадобятся размеры гипотенузы. Вычислим ее:
Теперь найдем, чему будет равна высота:
Ответ 20,16
Задача №8
Боковая сторона равнобедренного треугольника равна 25, а основание равно 48. Найдите площадь этого треугольника.
Решение.
В этой задаче, площадь треугольника найдем по формуле Герона. Для этого нужно знать полупериметр (периметр, деленный на 2) треугольника и длину каждой стороны.
В равнобедренном треугольнике, боковые стороны равны. Найдем периметр треугольника. Периметр треугольника – это сумма всех длин сторон треугольника
Ответ 168
Задача №9
В прямоугольном треугольнике гипотенуза равна 82, а один из острых углов равен 45°. Найдите площадь треугольника.
Решение
Если в прямоугольном треугольнике, один из острых углов равен 45 градусам, то и второй острый угол равен 45 градусам, так как сумма острых углов в прямоугольном треугольнике равна 90 градусов. Если в треугольнике два угла равны, то этот треугольник равнобедренный.
В нашем случает получается треугольник прямоугольный и равнобедренный т.е. катеты треугольника равны. Найдем катеты прямоугольного треугольника через теорему Пифагора.
Пусть катеты прямоугольного треугольника это Х
Ответ 1681
Задача №10
Решение
Третья теорема. Теорема о площади треугольника (9 класс)
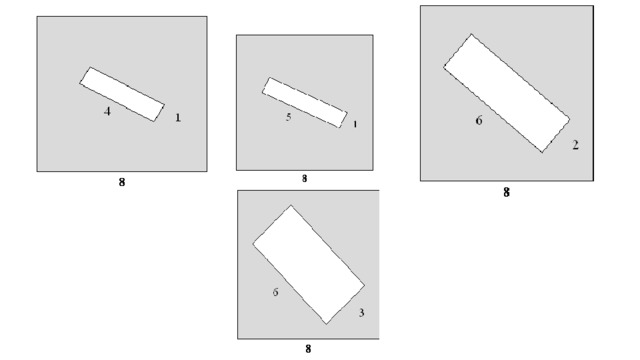
Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
Ответ 50
Спасибо, что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог
Рассмотрим задачи,в которых требуется найти площадь треугольника изображённого на клетчатой бумаге.
Начнем с прямоугольных треугольников.
Задача 1
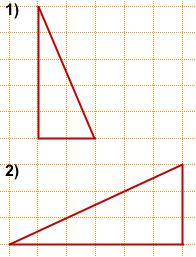 На клетчатой бумаге с размером клетки 1×1 изображен прямоугольный треугольник.
На клетчатой бумаге с размером клетки 1×1 изображен прямоугольный треугольник.
Найти его площадь.
Решение:
Площадь прямоугольного треугольника будем искать с помощью формулы
![]()
где a и b — катеты.
Длину катетов считаем по клеточкам.
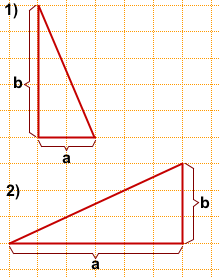 1) a=2, b=5,
1) a=2, b=5,
![]()
2) a=6, b=3,
![]()
Задача 2
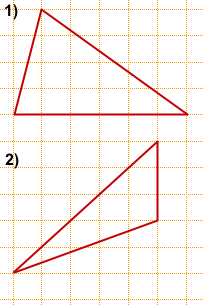 На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найти его площадь.
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найти его площадь.
Решение:
Чаще всего площадь произвольного треугольника, изображённого на клетчатой бумаге, ищут по формуле
![]()
где a — сторона треугольника, ha — высота, проведённая к этой стороне.
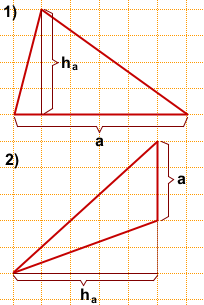 a и ha вычисляем по клеточкам (одна из этих величин должна лежать на горизонтальной линии, другая — на вертикальной).
a и ha вычисляем по клеточкам (одна из этих величин должна лежать на горизонтальной линии, другая — на вертикальной).
1) a=6, ha=4,
![]()
2) a=3, ha=5,
![]()
А как найти площадь, если ни одна из сторон треугольника не лежит на горизонтальной или вертикальной линии клеток?
Иногда площадь треугольника можно найти как разность площадей других фигур.
Задача 3
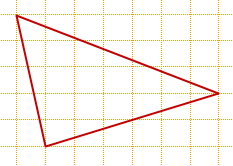
На клетчатой бумаге с размером клетки 1×1 изображён треугольник.
Найдите его площадь.
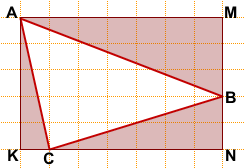
Решение:
Обозначим вершины треугольника, площадь которого мы ищем, через A, B и C.
Площадь треугольника ABC можно найти как разность площадей прямоугольника AMNK и треугольников AKC, AMB и CBN:
![]()
Площадь прямоугольника найдём по формуле S=ab.
![]()
Площади прямоугольных треугольников найдём по формуле
![]()
где a и b — катеты.
![]()
![]()
![]()
Отсюда
![]()
В 18 задании необходимо найти какую-либо часть фигуры, нарисованной на клетчатой бумаге. Именно клетчатая бумага 1×1 является особенностью данного задания. Задание не сложное, необходимо внимательно посчитать количество клеток и при необходимости выполнить действие. Опять же нам понадобятся элементарные знания геометрии для успешного решения данного задания. Ниже я разобрал типичные задания.
На клетчатой бумаге размером 1×1 изображён ромб. Найдите длину его большей диагонали.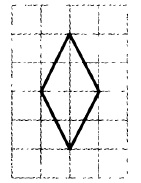
Внимательно смотрим на рисунок и видим, что длина одной диагонали ромба равна 2, а второй 4. Так как нас спрашивают длину большей диагонали, то в ответе нужно указать 4.
Ответ: 4
pазбирался: Даниил Романович | обсудить разбор | оценить
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии.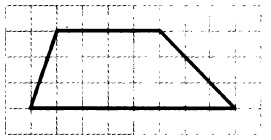
Мы знаем, что средняя линия равна полусумме оснований. Нижнее основание данной трапеции равно 8 клеткам, а верхнее – 4 клеткам. Полусумма оснований:
( 8 + 4 ) / 2 = 6
Ответ: 6
pазбирался: Даниил Романович | обсудить разбор | оценить
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.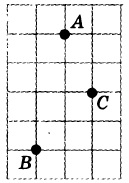
Проведем необходимые отрезки:
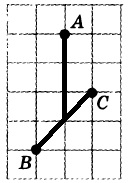
Из рисунка можно вычислить длину – это 3.
Ответ: 3
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите тангенс острого угла, изображённого на рисунке.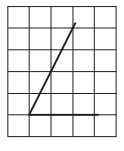
Детализируем рисунок. Проведем вертикальную линию, которая отсекает от сторон угла 2 клетки по горизонтали . В результате получен прямоугольный ∆АВС:
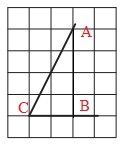
Чтобы получить ответ на вопрос задачи, требуется найти tg∠C.
Согласно определению тангенса, из треугольника ∆АВС можем записать:
tg∠C=AB/BC.
По рисунку подсчитываем длины отрезков АВ и ВС (по кол-ву клеток):
АВ=4, ВС=2.
Получаем:
tg∠C=4/2=2.
Ответ: 2
pазбирался: Даниил Романович | обсудить разбор | оценить
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.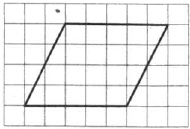
Площадь параллелограмма вычисляется так:
S=a·ha
Обозначим a и ha на рисунке:
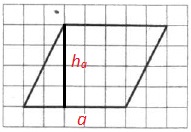
Теперь определим их длины по рисунку:
a=5; ha=4.
Вычисляем искомую площадь:
S=5·4=20.
Ответ: 20
pазбирался: Даниил Романович | обсудить разбор | оценить
На клетчатой бумаге с размером клетки 1×1 изображен ромб. Найдите площадь этого ромба.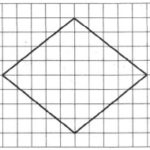
Площадь ромба будем искать через его диагонали:
S=d1·d2/2
Линии диагоналей обозначим на рисунке красным:
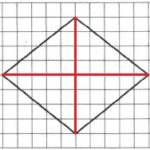
Обозначим меньшую диагональ через d1, большую – через d2 (можно наоборот). Определим их длины из рисунка:
d1=8; d2=10.
Находим площадь фигуры:
S=8·10/2=40
Ответ: 40
pазбирался: Даниил Романович | обсудить разбор | оценить
На клетчатой бумаге с размером клетки 1х1 изображен треугольник АВС. Найти длину его средней линии, параллельной стороне АС.

Для решения задачи надо вспомнить свойство средней линии: она параллельна основанию и равна его половине. Следовательно, чтобы найти длину средней линии, надо сторону треугольника разделить пополам. Найдем сторону треугольника, которой параллельна средняя линия, т.е. АС, сосчитав клетки, получим, что АС равна 8. Значит, средняя линия равна 8:2=4.
Ответ: 4
pазбирался: Даниил Романович | обсудить разбор | оценить
Советы
Три документа, с изучения которых следует начать подготовку к ЕГЭ и ОГЭ 2019:
1) Демовариант — познакомит Вас с экзаменационными заданиями
2) Спецификатор — поможет разобраться в уровнях сложности заданий и распределении времени на решение каждого
3) Кодификатор — содержит темы, знание которых проверяется на экзамене
Площадь треугольника требуется уметь находить, чтобы успешно решить модуль «Геометрия» в ОГЭ. Умение находить площадь треугольника является одним из основополагающих умений в геометрии. Для того, чтобы находить площадь треугольника в заданиях ОГЭ — нужно иметь представления о том, по каким формулам вообще находится площадь треугольника. Ниже мы приводим их все, а также даем анализ того, как часто встретятся вам эти формулы при выполнении заданий по геометрии в ОГЭ.
Задачи самые разнообразные, как и треугольники, как и методы их решения. Однако, для того, чтобы решать такие задачи, нам понадобятся формулы и общие сведения.
Площадь треугольника. Формулы. Задачи.
1. Формула нахождения площади треугольника по двум сторонам и углу между ними
Эта формула считается общей, ее очень часто используют, особенно если в треугольнике известен какой-либо угол. Ее кратко называют так «площадь треугольника через синус». Итак, посмотрите на чертеж — нам дан треугольник ABC, известны две его стороны и угол между ними. Тогда площадь треугольника находится по формуле: 
 Задачи на определение площади треугольника при заданных сторонах треугольника и углу между ними.
Задачи на определение площади треугольника при заданных сторонах треугольника и углу между ними.
Задача 1. Найдите площадь треугольника, две стороны которого равны 19 и 18, а угол между ними равен 300. Решение. Используем формулу площади треугольника через синус: ![]() Ответ: 85,5 Задача 2. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 150 0 . Боковая сторона треугольника равна 2. Найдите площадь этого треугольника. Решение. Нарисуем треугольник. Обозначим его вершины — A, B, C. Значит, нам дано: <ABC=1500. AB=BC=2. Тогда для того, чтобы найти площадь треугольника, воспользуемся формулой нахождения площади треугольника по двум сторонам и углу между ними:
Ответ: 85,5 Задача 2. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 150 0 . Боковая сторона треугольника равна 2. Найдите площадь этого треугольника. Решение. Нарисуем треугольник. Обозначим его вершины — A, B, C. Значит, нам дано: <ABC=1500. AB=BC=2. Тогда для того, чтобы найти площадь треугольника, воспользуемся формулой нахождения площади треугольника по двум сторонам и углу между ними:

 В этой задаче мы применили метод приведения для тригонометрических функций.
В этой задаче мы применили метод приведения для тригонометрических функций.
Ответ: 1.
2. Площадь треугольника через высоту.
Самая любимая школьниками формула определения площади треугольника — определение площади через высоту. В этой формуле всего нужно знать две величины — основание треугольника и высоту проведенную из вершины треугольника к этому основанию — смотрите рисунок.

Очень удобная формула для определения любого треугольника, если известны любые три его размера.
3. Площадь равнобедренного треугольника.
Равнобедренным называется треугольник, у которого две стороны равны. Нахождение площади равнобедренного треугольника ничем не отличается от нахождения площади обыкновенного треугольника, разве что формула площади равнобедренного треугольника несколько упрощается. Например, если дана боковая сторона треугольника и угол при вершине, то формула нахождения площади будет выглядеть так: ![]()
Вообще говоря, нет необходимости выводить и тем более запоминать некую мифическую формулу площади равнобедренного треугольника. Нужно просто помнить, что равнобедренный треугольник всего лишь частный случай общего, обыкновенного треугольника и все те формулы, которые применимы для нахождения площади треугольника, будут применимы и для равнобедренного треугольника.
Гораздо важнее не забыть свойства равнобедренного треугольника — высота (перпендикуляр), проведенная к основанию равнобедренного треугольника, есть медиана (делит основание пополам), биссектриса (делит угол напротив основания пополам). Углы при основании равнобедренного треугольника равны.

4. Площадь треугольника по координатам вершин
Никакой волшебной формулы тут нет — вы просто, используя координаты вершин, находите длины сторон треугольника, а затем подставляете их в формулу Герона.
5. Формула Герона для нахождения площади треугольника
,
где p — полупериметр треугольника, который находится по формуле:
а, b и c — стороны треугольника.
Таким образом, зная формулы, найти площадь треугольника не составит никакого труда.
Как находить площадь треугольника в заданиях ОГЭ.
В заданиях ОГЭ обычно площадь треугольника просят найти с помощью самой простой формулы — через основание и высоту.
Очень и очень редко встречается задача нахождения площади треугольника через две стороны и синус угла между ними, а уж формула Герона вообще не встречается, разве что вы можете ее использовать, если она вам очень нравится, да и то — в задачах второй части ОГЭ.


Площадь треугольника.

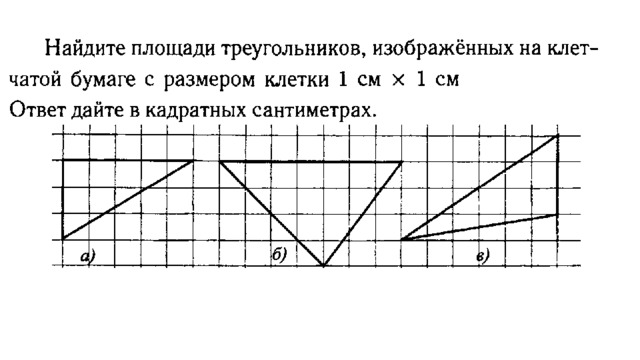
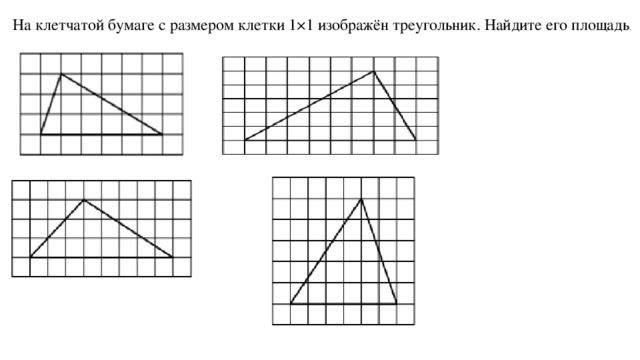
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь .



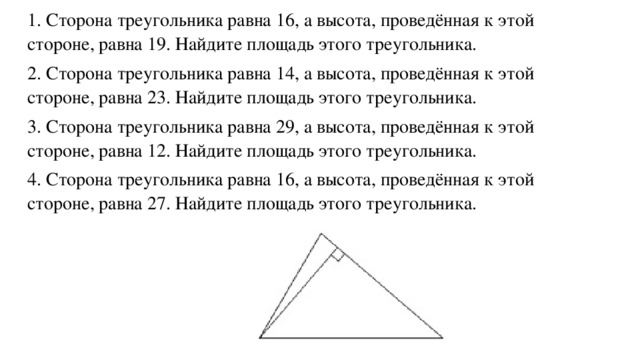
1. Сторона треугольника равна 16, а высота, проведённая к этой стороне, равна 19. Найдите площадь этого треугольника.
2. Сторона треугольника равна 14, а высота, проведённая к этой стороне, равна 23. Найдите площадь этого треугольника.
3. Сторона треугольника равна 29, а высота, проведённая к этой стороне, равна 12. Найдите площадь этого треугольника.
4. Сторона треугольника равна 16, а высота, проведённая к этой стороне, равна 27. Найдите площадь этого треугольника.

1. В треугольнике со сторонами 16 и 2 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?
2. В треугольнике со сторонами 15 и 3 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?
3. В треугольнике со сторонами 2 и 4 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 2. Чему равна высота, проведённая ко второй стороне?

1. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 40 и 85.
2. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 36 и 39.
3. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 32 и 68.

1. Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.
2. Боковая сторона равнобедренного треугольника равна 25, а основание равно 30. Найдите площадь этого треугольника.
3. Боковая сторона равнобедренного треугольника равна 25, а основание равно 48. Найдите площадь этого треугольника.

1. Площадь прямоугольного треугольника равна 722√23. Один из острых углов равен 30°. Найдите длину катета, лежащего напротив этого угла.
2. Площадь прямоугольного треугольника равна 512√3. Один из острых углов равен 30°. Найдите длину катета, лежащего напротив этого угла.
3. Площадь прямоугольного треугольника равна 128√3. Один из острых углов равен 30°. Найдите длину катета, лежащего напротив этого угла.

1. В прямоугольном треугольнике один из катетов равен 4, а острый угол, прилежащий к нему, равен 45° . Найдите площадь треугольника.
2. В прямоугольном треугольнике один из катетов равен 7, а острый угол, прилежащий к нему, равен 45° . Найдите площадь треугольника.
3. В прямоугольном треугольнике один из катетов равен 24, а острый угол, прилежащий к нему, равен 45° . Найдите площадь треугольника.

1. Площадь прямоугольного треугольника равна 8√3/3. Один из острых углов равен 60°. Найдите длину катета, лежащего напротив этого угла.
2. Площадь прямоугольного треугольника равна 200√3/3. Один из острых углов равен 60°. Найдите длину катета, лежащего напротив этого угла.
1. Площадь прямоугольного треугольника равна 512√3 . Один из острых углов равен 60° . Найдите длину катета, прилежащего к этому углу.
2. Площадь прямоугольного треугольника равна 2√3 . Один из острых углов равен 60° . Найдите длину катета, прилежащего к этому углу.

1. В прямоугольном треугольнике гипотенуза равна 70, а один из острых углов равен 45° . Найдите площадь треугольника.
2. В прямоугольном треугольнике гипотенуза равна 82, а один из острых углов равен 45° . Найдите площадь треугольника.
3. Периметр равнобедренного треугольника равен 216, а боковая сторона — 78. Найдите площадь треугольника.
4. Периметр равнобедренного треугольника равен 196, а боковая сторона — 74. Найдите площадь треугольника.
5. Периметр равнобедренного треугольника равен 196, а основание — 48. Найдите площадь треугольника.
6. Периметр равнобедренного треугольника равен 324, а основание — 160. Найдите площадь треугольника.
Площадь треугольника

Задача
1. В
треугольнике одна из сторон равна 27, а опущенная на нее высота – 11. Найдите
площадь треугольника.
Решение: Площадь треугольника = ½
основания*высоту
Пл.треугольника
= ½*27*11=148,5
Ответ:
148,5
Задача
2. Два
катета прямоугольного треугольника равны 4 и 9. Найдите площадь этого
треугольника.
Решение:
Пл.прямоугольного
треуг. = половине произведения катетов.
Пл.прямоуг.треуг.=(4*9):2=36:2=18
Ответ: 18
Задача
3. Периметр
равнобедренного треугольника равен 144, а основание – 64. Найдите площадь
треугольника.
Решение:
1) Т.к.
Треугольник равнобедренный, из этого следует, что две стороны равны АС=СВ,
найдем длину этих  сторон:
сторон:
АС=СВ=(144-64):2=40.
2)
Формула Герона:
Найдем
полупериметр, т.к. периметр = 144, то полупериметр = 144:2=72.
![]()
Ответ: 768
Задача
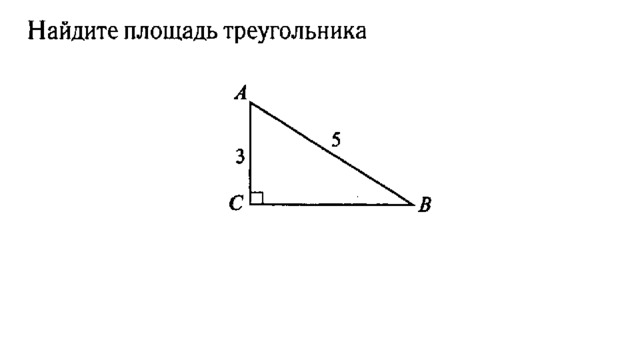
4. Найдите
площадь треугольника.

Решение: Для формулы нам необходимо
знать основание и высоту
![]() Основание=32+11=43.
Основание=32+11=43.
Высота
= 60.
S треуг.= ½*60*43=1290
Ответ: 1290
![]()
32+11=43
Задача
5.

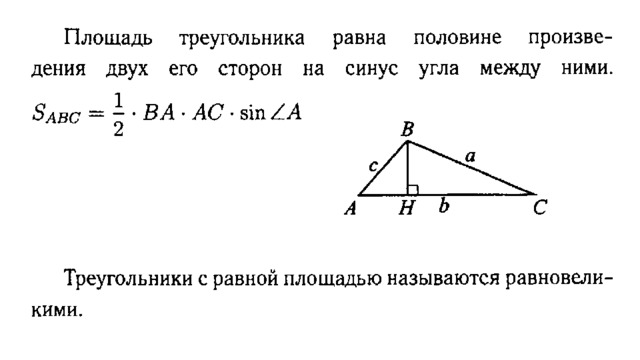
 |

6
3
Решение:
Задачу
можно решить по формуле Пика, можно по формуле площади треугольника.
Считаем
по клеточкам основание =3, высота = 6.
S=1/2*3*6= 9
Ответ: 9
Задачи
для самостоятельного решения:
1)
В
треугольнике одна из сторон равна 14, а опущенная на нее высота – 31. Найдите
площадь треугольника.
2)
Сторона
треугольника равна 16, а высота, проведённая к этой стороне, равна 19. Найдите
площадь этого треугольника.
3)
Два катета прямоугольного треугольника равны 7 и 12. Найдите площадь этого
треугольника.
4) Два катета
прямоугольного треугольника равны 18 и 7. Найдите площадь этого треугольника.
5) Периметр
равнобедренного треугольника равен 162, а основание – 72. Найдите площадь
треугольника.
6) Найдите площадь
треугольника

7) Найдите площадь
треугольника

8) Найдите площадь треугольника:

9) Найдите площадь треугольника

10) 
11) 
12) 
13)
14) 15)
15) 
16)
Проверить решение можно по ссылке:
https://onlinetestpad.com/hnl6ukjjcnpgo
