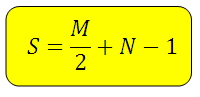Как найти площадь треугольника по формуле пика - Сайт, где вы сможете решить свои вопросы

Каждому из нас нередко приходилось считать площадь решётчатого многоугольника (изображённого, например, на клетчатой бумаге). В основном, это делают ещё по известным со школы формулам. Но в этом случае для каждой фигуры приходится помнить выражение её площади.
Не легче ли использовать одну формулу для всех многоугольников?
— Сказка? — Нет, теорема Пика!

• Названа она в честь Георга Пика (нет, не оружия или покемона), доказавшего её в 1899 году.

Формулировка звучит так:
S = В + Г / 2 − 1, где S — площадь многоугольника, В — количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника.
• Важное замечание: формула справедлива только для многоугольников, у которых вершины расположены в узлах решетки.

Например, для многоугольника на рисунке, В=7 (красные точки), Г=8 (зелёные точки), поэтому S = 7 + 8/2 – 1 = 10 квадратных единиц.

Докажем теорему Пика:
• Рассмотрим прямоугольник со сторонами, лежащими на линиях решетки. Пусть длины его сторон равны a и b. Имеем в этом случае В = (a-1)(b-1), Г = 2a+2b и, по формуле Пика, S = (a-1)(b-1)+a+b-1 = ab .
• Рассмотрим теперь прямоугольный треугольник с катетами, лежащими на осях координат. Такой треугольник получается из прямоугольника со сторонами a и b, рассмотренного в предыдущем случае, разрезанием его по диагонали. Пусть на диагонали лежат c целочисленных точек. Тогда для этого случая В = ((a-1)(b-1)-c+2)/2, Г = (2a+2b)/2+c-1 и получаем, что S = ab/2.
• Теперь рассмотрим произвольный треугольник. Его можно получить, отрезав от прямоугольника несколько прямоугольных треугольников (см. рисунок). Поскольку и для прямоугольника, и для прямоугольного треугольника формула Пика верна, мы получаем, что она будет справедлива и для произвольного треугольника.

• Остается сделать последний шаг: перейти от треугольников к многоугольникам. Любой многоугольник можно триангулировать, т.е. разбить на треугольники (например, диагоналями). Отсюда по индукции следует, что формула Пика верна для любого многоугольника. чтд

К сожалению, эта столь простая и красивая формула плохо обобщается на высшие размерности.
Наглядно показал это Рив, предложив в 1957 г. рассмотреть тетраэдр (называемый теперь тетраэдром Рива) со следующими вершинами:
A(0,0,0), B(1,0,0), C(0,1,0), D(1,1,k)
Тогда этот тетраэдр ABCD при любых k не содержит внутри ни одной точки с целочисленными координатами, а на его границе — лежат только четыре точки A, B, C, D. Таким образом, объём и площадь поверхности этого тетраэдра могут быть разными, в то время как число точек внутри и на границе — неизменны; следовательно, формула Пика не допускает обобщений даже на трёхмерный случай.
Тем не менее, некоторое подобное обобщение на пространства большей размерности всё же имеется, — это многочлены Эрхарта, но они весьма сложны, и зависят не только от числа точек внутри и на границе фигуры.

Специально для ЖЖ матфака, Сергей Романов.

Источник

Формула Пика. Рассказ о формуле, при помощи которой можно находить площадь фигуры построенной на листе в клетку (треугольник, квадрат, трапеция, прямоугольник, многоугольник). Это формула Пика.

Она секретной не является. Информация о ней в интернете имеется, но многим материал статьи будет крайне полезен. Об этой формуле обычно рассказывается применительно к нахождению площади треугольника. На примере треугольника мы её и рассмотрим.

В задачах, которые будут на ЕГЭ есть целая группа заданий, в которых дан многоугольник построенный на листе в клетку и стоит вопрос о нахождении площади. Масштаб клетки это один квадратный сантиметр.

ФОРМУЛА ПИКА

Площадь искомой фигуры можно найти по формуле:

М – количество узлов на границе треугольника (на сторонах и вершинах)

N – количество узлов внутри треугольника

*Под «узлами» имеется ввиду пересечение линий.

Найдём площадь треугольника:

Отметим узлы:

1 клетка = 1 см

M = 15 (обозначены красным)

N = 34 (обозначены синим)

Ещё пример. Найдём площадь параллелограмма:

Отметим узлы:

M = 18 (обозначены красным)

N = 20 (обозначены синим)

Найдём площадь трапеции:

Отметим узлы:

M = 24 (обозначены красным)

N = 25 (обозначены синим)

Найдём площадь многоугольника:

Отметим узлы:

M = 14 (обозначены красным)

N = 43 (обозначены синим)

Понятно, что находить площадь трапеции, параллелограмма, треугольника проще и быстрее по соответствующим формулам площадей этих фигур. Но знайте, что можно это делать и таким образом.

А вот когда дан многоугольник, у которого пять и более углов эта формула работает хорошо.

Теперь взгляните на следующие фигуры:

Это типовые фигуры, в заданиях стоит вопрос о нахождении их площади. Такие или подобные им будут на ЕГЭ. При помощи формулы Пика такие задачи решаются за минуту. Например, найдём площадь фигуры:

Отметим узлы:

M = 11 (обозначены красным)

N = 5 (обозначены синим)

Ответ: 9,5

Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.

Посмотреть решение

Конечно, можно и эти «микрофигурки» дробить на более простые фигуры (треугольники, трапеции). Способ решения выбирать вам.

Рассмотрим подход оговоренный в статье “Площадь четырёхугольника. Универсальный способ“.

Найдём площадь фигуры:

Опишем около неё прямоугольник:

Из площади прямоугольника (в данном случае это квадрат) вычтем площади полученных простых фигур:

Ответ: 4,5

В будущем будем рассматривать задания на нахождение площади, связанные с окружностями построенными на листе в клетку, не пропустите! На этом всё. Успехов вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Источник

У этого термина существуют и другие значения, см. Теорема Пика.

Формула Пи́ка (или теорема Пи́ка) — классический результат комбинаторной геометрии и геометрии чисел,
даёт выражение для площади многоугольника с целочисленными вершинами.

Названа в честь Георга Пика, доказавшего её в 1899 году.

Формулировка[править | править код]

В = 7, Г = 8,
В + Г/2 − 1 = 10

Площадь многоугольника с целочисленными вершинами^[1] равна
${displaystyle {text{В}}+{dfrac {text{Г}}{2}}-1}$ ,
где В — количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника.

Следствия[править | править код]

Площадь треугольника с вершинами в узлах и не содержащего узлов ни внутри, ни на сторонах (кроме вершин), равна 1/2.
- Этот факт даёт геометрическое доказательство формулы для разности подходящих дробей цепной дроби.

Вариации и обобщения[править | править код]

Контрпример к аналогу теоремы Пика в размерности 3.

Многочлен Эрара даёт один из вариантов обобщения формулы Пика на старшие размерности.

где суммирование ведётся по всем целочисленным точкам

телесный угол

при

; если

лежит внутри

, то считается что

.^[2]

${displaystyle V(M)={tfrac {1}{omega _{n}}}cdot sum _{v}alpha (v),}$

где $omega _{n}$

обозначает площадь единичной сферы в ${displaystyle mathbb {E} ^{n}}$

Примечания[править | править код]

↑ Точка координатной плоскости называется целочисленной, если обе её координаты целые.
↑ Tabachnikov, Sergei, Pierre Deligne, and Sinai Robins. The Ice Cube Proof (англ.) // The Mathematical Intelligencer. — 2014. — Vol. 36, no. 4. — P. 1-3.

Литература[править | править код]

В. В. Прасолов. Задачи по планиметрии. — М.: МЦНМО, 2001. — 584 с. — ISBN 5-900916-82-0.
А. Кушниренко. Целые точки в многоугольниках и многогранниках // Квант. — 1977. — № 4. — С. 13—20.

Источник

Скачать материал

Сейчас обучается 140 человек из 50 регионов

Сейчас обучается 48 человек из 26 регионов

Сейчас обучается 75 человек из 34 регионов

Описание презентации по отдельным слайдам:

1 слайд

Площадь треугольника.
Решение одной задачи несколькими способами
Давыдова О.А.
учитель математики
МОУ «ООШ № 17»

2014-2015 учебный год
2 слайд

Совершенствовать навыки решения задач на применение различных способов решений при нахождении площадей геометрических фигур на примере заданий №11 по математике.
Развивать умения анализировать, сопоставлять, логически мыслить, обобщать; развивать внимание, память, самостоятельность.
Воспитывать ответственное отношение к учебному труду, настойчивость для достижения конечного результата, умение работать самостоятельно, осуществлять самоконтроль.
3 слайд

Модуль «Геометрия» № 11
Нахождение площади фигур
На клетчатой бумаге с клетками размером
1 см х 1 см
изображен треугольник
(см. рисунок).
Найдите его площадь в квадратных сантиметрах.
4 слайд

1 способ. «Считаем по клеткам».
2 способ. «Формула площади фигуры».
3 способ. «Сложение площадей фигур».
4 способ. «Вычитание площадей фигур».
5 способ. «Формула Пика».
Способы решений
5 слайд

7
3
1
2
4
5
6
8
9
10
1 способ
« Считаем по клеткам»
1.Посчитаем количество полных клеток внутри данного треугольника.
10
2.Дополним неполные клетки друг другом до полных клеток.
5
3. Сложим полученные количества полных клеток:
10+5=15
Ответ: 15
1
2
3
4
5
6 слайд

а
h
6
5
«Формула площади фигуры»
Площадь искомого треугольника найдем по формуле:
Sтр=(а•h)/2,
где а – основание треугольника,
h – высота, проведенная к этому основанию.
а=6, h=5
Получаем Sтр=(6•5)/2=15
Ответ: 15
2 способ
7 слайд

«Сложение площадей фигур»
1.Разобьем данный треугольник на два прямоугольных треугольника, для этого проведем высоту.
2.Найдем площадь прямоугольного треугольника S1 :
S1 = (5Х5)/2=12,5
3.Найдем площадь прямоугольного треугольника S2:
S2 = (5х1)/2=2,5
4.Площадь искомого треугольника найдем по формуле:
Sтр=S1+S2
Sтр=12,5+2,5=15
Ответ: 15
5
1
5
3 способ
S1
S2
8 слайд

5
6
5
5
1
S1
S2
«Вычитание площадей фигур»
1.Достроим до прямоугольника со сторонами 5 и 6.
2.Найдем площадь прямоугольника:
Sпр=5Х6=30
3.Найдем площадь прямоугольного треугольника S1 :
S1 = (5Х5)/2=12,5
4.Найдем площадь прямоугольного треугольника S2:
S2 = (5х1)/2=2,5
5.Площадь искомого треугольника найдем по формуле:
Sтр=Sпр-(S1+S2)
Sтр=30-(12,5+2,5)= 15
Ответ: 15
4 способ
9 слайд

5 способ
«Формула Пика»
Площадь искомого треугольника найдем по формуле Пика:
S=Г/2+В-1,
где Г –количество узлов на границе треугольника(на сторонах и вершинах),
В – количество узлов внутри треугольника.
Г=
Получаем S=12/2+10-1=15
Ответ: 15
В=
12,
10
11 слайд

Диаграмма популярности способов решения
12 слайд

На клетчатой бумаге с клетками размером 1 см х 1 см изображен треугольник (см. рисунок).
Найдите его площадь в квадратных сантиметрах.
Решение.
Данный треугольник – прямоугольный. Воспользуемся формулой площади прямоугольного треугольника:
S=1/2ab,
где a и b – катеты треугольника.
a=2, b=6.
Получаем S = ½ ·2·6 = 6.
Ответ: 6
2
6
13 слайд

На клетчатой бумаге с клетками размером 1 см х 1 см изображен треугольник (см. рисунок).
Найдите его площадь в квадратных сантиметрах.
Решение.
Воспользуемся формулой Пика:

S=Г/2+В-1
Г = 5,
В = 9
Получаем S = 5/2 + 9 – 1 =
10,5
Ответ: 10,5
14 слайд

На клетчатой бумаге с клетками размером 1 см х 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
Площадь искомого треугольника найдем по формуле:
Sтр=(а•h)/2,
Решение.
где а – основание треугольника,
h – высота, проведенная к этому основанию.
Длина этого отрезка равна
h
a
Значит, а = 6 ,
h = 2
Sтр= (6 · 2 )/2 = 12.
Ответ: 12
15 слайд

На клетчатой бумаге с клетками размером 1 см х 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах.
Решение.
1. Разобьем данную фигуру на 4 части. Получилось 4 прямоугольных треугольника.
1 способ.
2. Найдем площадь одного треугольника:
S =
2
(2·3)/2
3
= 3
3. Искомую площадь фигуры находим по формуле: S = 4·Sтр ,
S = 4·3=12.
Ответ: 12.
2 способ.
Данная фигура – ромб.
Площадь ромба находим по формуле:
S = (d1·d2)/2
d1
d2
d1 = 4, d2 = 6.
Получаем S = (4·6)/2 = 12.
16 слайд

На клетчатой бумаге с клетками размером 1 см х 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах.
Решение.
1. Достроим данную фигуру до равностороннего треугольника.
Найдем площадь этого треугольника: S =
6
4
(6·4)/2 =12
2. Найдем площадь другого треугольника:
2
S = (6·2)/2 = 6
3. Площадь искомой фигуры находим как разность площадей:
S = 12 – 6 = 6.
Ответ: 6.
17 слайд

Если вы хотите научиться плавать, то смело входите в воду,
а если хотите научиться решать задачи, то решайте их!
Д. Пойа
Успехов при подготовке к ГИА по математике!!!

Удачной сдачи экзамена!
18 слайд

В презентации использованы:
http://www.proshkolu.ru/user/Nadegda797/file/635838/&newcomment=803270#comment803270 – анимационные картинки
http://ru.wikihow.com
http://kakimenno.ru/raznoe/96-kak-nayti-ploschad-treugolnika.html
http://matematikalegko.ru/formuli/ploshhad-figury-na-liste-v-kletku-formula-pika.html
http://www.webmath.ru/
http://angrenkova.ucoz.ru/load/zadanija_v10/zadanija_v3/vychislenie/8-1-0-67
http://nsportal.ru/
http://www.etudes.ru/

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 257 752 материала в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Другие материалы

19.06.2018
2965
5

Рейтинг:
5 из 5

19.06.2018
2235
53

Рейтинг:
5 из 5

19.06.2018
1244
16

Рейтинг:
5 из 5

19.06.2018
1584
5

19.06.2018
2117
76

Вам будут интересны эти курсы:

Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Организация научно-исследовательской работы студентов в соответствии с требованиями ФГОС»
Курс профессиональной переподготовки «Клиническая психология: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Применение MS Word, Excel в финансовых расчетах»
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Учебная деятельность по предметной области «Черчение»: основы предмета и реализация обучения в условиях ФГОС»
Курс повышения квалификации «Актуальные вопросы банковской деятельности»
Курс профессиональной переподготовки «Организация маркетинговой деятельности»
Курс профессиональной переподготовки «Технический контроль и техническая подготовка сварочного процесса»

Источник

Вокруг формулы Пика

Уровень сложности
Средний

Время на прочтение
2 мин

Количество просмотров 2.2K

Как найти площадь произвольного многоугольника с вершинами в узлах клетчатой бумаги?

В простых ситуациях его можно разбить на треугольники (рис. 1а) или, наоборот, достроить до прямоугольника (рис. 1б). Но как быть в общем случае? Посмотрите, скажем, на рисунок 1в.

Оказывается, достаточно подсчитать числовершин внутри многоугольника и число на его границе — тогда его площадьбудет равна

$S = I + frac B 2 − 1.$

Это формула называется формулой Пика в честь австрийского математика Георга Пика (1859–1942), открывшего её в 1899 году. Так, для многоугольника на рисунке 1в имеем

, , поэтому $S = 13 + frac {20} {2} − 1 = 22.$

Формула выглядит удивительно просто. Интересно, столь же просто её доказать?

Этап 1: ШАГ ИНДУКЦИИ. Предположим, что многоугольник разбит диагональю на два, для которых формула доказана. Тогда несложно показать, что она верна и для.

Этап 2: ТРИАНГУЛЯЦИЯ. Многократно проводя внутренние диагонали, разобьём наш многоугольник на элементарные треугольники (не содержащие узлов ни на границе, ни внутри, кроме вершин). Для такого треугольникаипоэтому площадь должна быть равна

Этап 3: БАЗА ИНДУКЦИИ. Остаётся доказать, что площадь элементарного треугольника равнаМы приведём важное и красивое рассуждение.

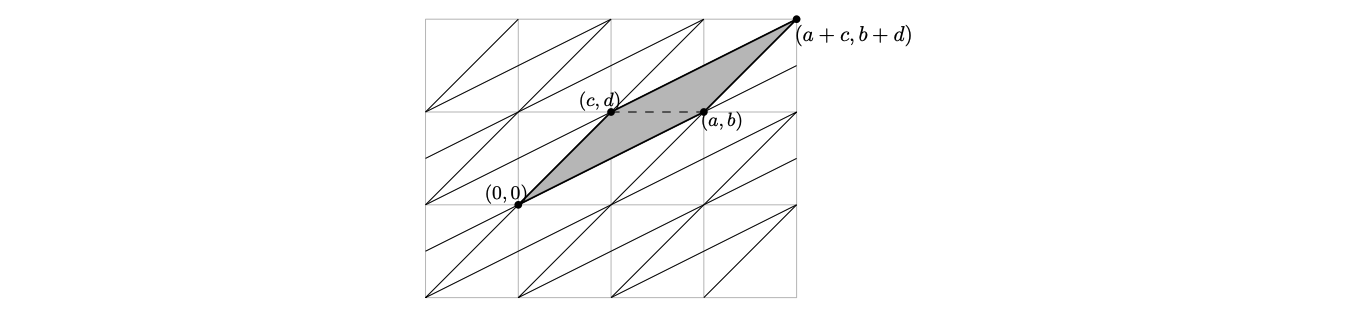
Пусть треугольник имеет вершины иДостроим его до параллелограмма, добавив вершину и замостим его копиями всю плоскость (рис. 2).

Элементарность нашего треугольника равносильна тому, что любой узелможно получить из узлацелочисленными сдвигами сторониИными словами, для любых целыхинайдутся целыеитакие, что

$x(a, b) + y(c, d) = (e, f) Longleftrightarrow begin{cases} ax + cy = e \ bx + dy = f. end{cases}$

Неожиданно, геометрическая задача свелась к чисто алгебраической — системе линейных уравнений. Её решение даётся формулами Крамера

$x = frac {de − cf} ∆ , ;; y = frac {af − be} ∆ , ;;где ;; ∆ = ad − bc ;; — ;; textit {определитель} ;;системы .$

Хорошо известно, что определительпо модулю равен площади параллелограмма, построенного на векторахипоэтому нам надо доказать, что
Приимеема при
Так каквсегда должны быть целыми, то кратныоткудакратно , что возможно, лишь при Формула Пика доказана.

В заключение сделаем несколько замечаний.

Приведённое рассуждение с замещением плоскости на школьном языке иллюстрирует важные идеи высшей алгебры — описание базисов свободной абелевой группыи группы её автоморфизмов:

$Aut(mathbb Z^2) ; cong ; GL_2 (mathbb Z)=left{begin{pmatrix} a & b \ c & d end{pmatrix} middle| ad-bc=pm 1 right}.$
Последний факт можно обобщить на высшие размерности: $Aut(mathbb Z^n) ; cong ; { {A| det ;A = ±1} }.$
А вот формула Пика неверна уже в трёхмерном пространстве: объём многогранника с целыми вершинами не выражается через количества вершин внутри, на гранях и рёбрах.
Вместе с тем существуют варианты обобщения формулы Пика для некоторых классов целочисленных многомерных многогранников (например, с центрально-симметричными гранями).