Как найти площадь треугольника по клеткам огэ - Сайт, где вы сможете решить свои вопросы

Каталог заданий.
Треугольники общего вида

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Тип 18 № 341709

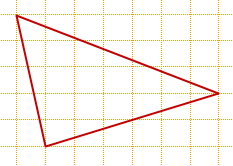
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его высоты, опущенной на сторону AC.

Решение

Помощь

Тип 18 № 348403

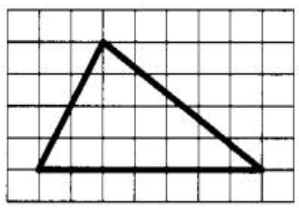
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.

Аналоги к заданию № 348403: 348641 348678 349113 … Все

Решение

Помощь

Тип 18 № 348480

На клетчатой бумаге с размером клетки 1х1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.

Аналоги к заданию № 348480: 348868 349105 349244 … Все

Решение

Помощь

Тип 18 № 348641

На клетчатой бумаге с размером клетки 1х1 изображён треугольник. Найдите его площадь.

Аналоги к заданию № 348403: 348641 348678 349113 … Все

Решение

Помощь

Тип 18 № 348678

На клетчатой бумаге с размером клетки 1х1 изображён треугольник. Найдите его площадь.

Аналоги к заданию № 348403: 348641 348678 349113 … Все

Решение

Помощь

Пройти тестирование по этим заданиям

Источник

Рассмотрим задачи,в которых требуется найти площадь треугольника изображённого на клетчатой бумаге.

Начнем с прямоугольных треугольников.

Задача 1

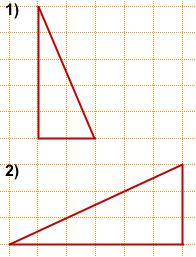
На клетчатой бумаге с размером клетки 1×1 изображен прямоугольный треугольник.

Найти его площадь.

Решение:

Площадь прямоугольного треугольника будем искать с помощью формулы

$[S = frac{1}{2}ab,]$

где a и b — катеты.

Длину катетов считаем по клеточкам.

1) a=2, b=5,

$[ S = frac{1}{2} cdot 2 cdot 5 = 5. ]$

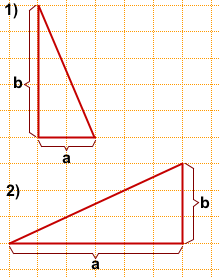
2) a=6, b=3,

$[ S = frac{1}{2} cdot 6 cdot 3 = 9. ]$

Задача 2

На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найти его площадь.

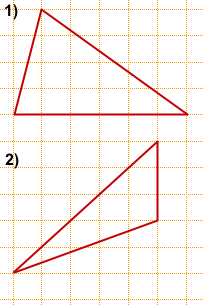
Решение:

Чаще всего площадь произвольного треугольника, изображённого на клетчатой бумаге, ищут по формуле

$[S = frac{1}{2}ah_a ,]$

где a — сторона треугольника, h_a — высота, проведённая к этой стороне.

a и h_a вычисляем по клеточкам (одна из этих величин должна лежать на горизонтальной линии, другая — на вертикальной).

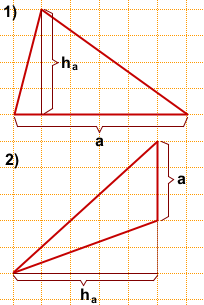
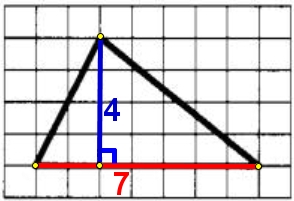
1) a=6, h_a=4,

$[ S = frac{1}{2}ah_a = frac{1}{2} cdot 6 cdot 4 = 12. ]$

2) a=3, h_a=5,

$[ S = frac{1}{2}ah_a = frac{1}{2} cdot 3 cdot 5 = 7,5. ]$

А как найти площадь, если ни одна из сторон треугольника не лежит на горизонтальной или вертикальной линии клеток?

Иногда площадь треугольника можно найти как разность площадей других фигур.

Задача 3

На клетчатой бумаге с размером клетки 1×1 изображён треугольник.

Найдите его площадь.

Решение:

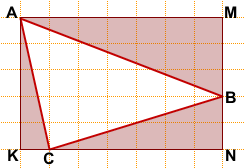
Обозначим вершины треугольника, площадь которого мы ищем, через A, B и C.

Площадь треугольника ABC можно найти как разность площадей прямоугольника AMNK и треугольников AKC, AMB и CBN:

$[S_{Delta ABC} = S_{AMNK} - S_{Delta AKC} - S_{Delta AMB} - S_{Delta CBN} .]$

Площадь прямоугольника найдём по формуле S=ab.

$[ S_{AMNK} = AM cdot AK = 7 cdot 5 = 35. ]$

Площади прямоугольных треугольников найдём по формуле

$[ S = frac{1}{2}ab, ]$

где a и b — катеты.

$[S_{Delta AKC} = frac{1}{2}AK cdot KC = frac{1}{2} cdot 5 cdot 1 = 2,5;]$

$[S_{Delta AMB} = frac{1}{2}AM cdot MB = frac{1}{2} cdot 7 cdot 3 = 10,5;]$

$[S_{Delta CBN} = frac{1}{2}CN cdot BN = frac{1}{2} cdot 6 cdot 2 = 6.]$

Отсюда

$[S_{Delta ABC} = 35 - 2,5 - 10,5 - 6 = 16.]$

Источник

Всем привет!

До ОГЭ по математике осталось совсем немного времени, но с другой стороны его не так уж и мало, чтобы успеть подготовиться и получить хороший результат на экзамене!

С этой статье мы разберем, как решать одно из самых простых заданий по математике, а именно №18. Кроме того, это задание относится к блоку “Геометрия”, а для того, чтобы успешно сдать ОГЭ, необходимо набрать как минимум два балла по геометрии! И спомощью этого задания вы уже получите как минимум один балл))

Даже если вам тяжело дается геометрия, это задание сможет решить каждый школьник..нужно просто повторить немного теории и научиться пользоваться некоторыми формулами, которые будут вам доступны на экзамене в форме справочных материалов.

В качестве примеров я взяла 5 заданий из сборника Ященко для подготовке к ОГЭ 2023. Итак, поехали.

Задание 1

На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки A, B и C. Найдите расстояние от точки A до отрезка BC.

Здесь все просто – расстояние от точки до прямой – это перпендикуляр, проведенный к этой прямой. Поэтому соединяем точки В и С в отрезок ВС, проводим к нему перпендикуляр из точки А. Считаем длину его по клеточкам:

Задание 18 ОГЭ по математике

Задание 2

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Для того, чтобы найти площадь трапеции, необходимо вспомнить формулу нахождения площади. Но на экзамене выдаются справочные материалы, поэтому найти эту формулу не составит никакого труда:

Формула площади трапеции

Осталось расшифровать эту формулу:

a и b – это основания трапеции, h -высота трапеции. Дальше считаем все по клеточкам и подставляем полученные значения в формулу:

В равнобедренной трапеции основания равны 2 и 6, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь этой трапеции.

Задание 3

На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.

Здесь, как и в предыдущем задании, мы можем воспользоваться справочными материалами и найти формулу площади треугольника.

Площадь треугольника

В этом задании используем 1 формулу, где а – это основание треугольника, h – высота, проведенная к основанию. В качестве основания мы берем сторону, расположенную слева, так как ее можно посчитать точно по клеточкам, соответственно и высоту проводим к этой стороне. Далее считаем клетки, подставляем в формулу и вычисляем площадь.

Вычисление площади

Задание 4

На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. … Найдите длину его средней линии, параллельной стороне AC.

Для решения этой задачи необходимо знать формулу нахождения средней линии. Но и здесь нам помогут справочные материалы. Там эта формула конечно же есть, даже если вы впервые слышите о таком понятии, как средняя линия, здесь все предельно ясно: нужно нижнее основание треугольника разделить на 2.

Средняя линия треугольника

Остается только посчитать длину нижнего основания по клеточкам и разделить полученное значение на два.

вычисление средней линии треугольника

Задание 5

На клетчатой бумаге с размером клетки 1×1 изображен ромб. Найдите площадь этого ромба.

Находим формулу площади ромба в справочных материалах:

Площадь ромба

Далее считаем диагонали ромба по клеточкам, подставляем полученные значения в формулу площади и вычисляем площадь ромба:

Задание 18 ОГЭ

Видеоразбор других прототипов 18 задания можно посмотреть здесь:

Подписывайтесь на канал, чтобы успешно подготовиться к ОГЭ 2023!

Если статья была полезна, не забудьте поставить лайк, это очень поможет ее продвижению!

Пишите в комментариях, какие еще задания ОГЭ подробно разобрать?

Источник

Площадь треугольника, изображённого на клетчатой бумаге

Рассмотрим задачи,в которых требуется найти площадь треугольника изображённого на клетчатой бумаге.

Начнем с прямоугольных треугольников.

На клетчатой бумаге с размером клетки 1×1 изображен прямоугольный треугольник.

Найти его площадь.

Площадь прямоугольного треугольника будем искать с помощью формулы

где a и b — катеты.

Длину катетов считаем по клеточкам.

1) a=2, b=5,

На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найти его площадь.

Чаще всего площадь произвольного треугольника, изображённого на клетчатой бумаге, ищут по формуле

где a — сторона треугольника, h_a — высота, проведённая к этой стороне.

Иногда площадь треугольника можно найти как разность площадей других фигур.

На клетчатой бумаге с размером клетки 1×1 изображён треугольник.

Найдите его площадь.

Обозначим вершины треугольника, площадь которого мы ищем, через A, B и C.

Площадь треугольника ABC можно найти как разность площадей прямоугольника AMNK и треугольников AKC, AMB и CBN:

Площади прямоугольных треугольников найдём по формуле

Геометрия. Урок 1. Задания. Часть 2.

№8. Найдите тангенс угла A O B , изображенного на рисунке.

Решение:

Опустим перпендикуляр A H на сторону O B .

Рассмотрим прямоугольный △ A O H :

Тангенс угла – отношение противолежащего катета к прилежащему.

tg ∠ A O H = A H O H = 4 2 = 2

№9. Найдите тангенс угла A треугольника A B C б изображённого на рисунке.

Решение:

Тангенс угла – это отношение противолежащего катета к прилежащему.

tg ∠ B A C = B C A C = 2 5 = 0,4

№10. На рисунке изображена трапеция A B C D . Используя рисунок, найдите sin ∠ B A H .

Решение:

Рассмотрим прямоугольный △ A B H :

Синус угла – отношение противолежащего катета к гипотенузе.

sin ∠ A = B H A B

Найдем A B по теореме Пифагора:

A B 2 = A H 2 + B H 2

A B 2 = 3 2 + 4 2

A B 2 = 9 + 16 = 25

A B = ± 25 = [ − 5 не подходит 5 подходит

sin ∠ A = B H A B = 4 5 = 0,8

№11. На рисунке изображен ромб A B C D . Используя рисунок, найдите tg ∠ O B C .

Решение:

Тангенс угла – это отношение противолежащего катета к прилежащему.

tg ∠ O B C = O C B O = 3 4 = 0,75

№12. На рисунке изображена трапеция A B C D . Используя рисунок, найдите cos ∠ H B A .

Решение:

Рассмотрим прямоугольный △ A B H :

Косинус угла – отношение прилежащего катета к гипотенузе.

cos ∠ A B H = B H A B

Найдем A B по теореме Пифагора:

A B 2 = A H 2 + B H 2

A B 2 = 6 2 + 8 2

A B 2 = 36 + 64 = 100

A B = ± 100 = [ − 10 не подходит 10 подходит

cos ∠ A B H = B H A B = 8 10 = 0,8

№13. Найдите тангенс угла, изображенного на рисунке.

Решение:

tg β = tg ( 180 ° − α ) = − tg α

Рассмотрим прямоугольный △ B C H .

Тангенс угла – отношение противолежащего катета к прилежащему.

tg α = C H B H = 3 1

tg β = − tg α = − 3

№14. Найдите тангенс угла A O B .

Решение:

Опустим высоту B H на сторону O A .

Рассмотрим прямоугольный △ O B H :

Найдем B H и O H по теореме Пифагора:

B H 2 = 2 2 + 8 2 = = 4 + 64 = 68

B H = ± 68 = ± 4 ⋅ 17 = ± 4 ⋅ 17 = ± 2 17 = [ − 2 17 не подходит 2 17 подходит

O H 2 = 1 2 + 4 2 = 1 + 16 = 17

O H = ± 17 = [ − 17 не подходит 17 подходит

Решение №2287 На клетчатой бумаге с размером клетки 1×1 изображён треугольник.

На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.

Источник: ОГЭ Ященко 2022 (36 вар)

Находим площадь треугольника по формуле:

Ответ: 14.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 5 / 5. Количество оценок: 1

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время

В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.

[spoiler title=”источники:”]

Геометрия. Урок 1. Задания. Часть 2.

Решение №2287 На клетчатой бумаге с размером клетки 1×1 изображён треугольник.

[/spoiler]

Источник

Площадь фигуры (треугольник, четырёхугольник, трапеция и др.) по клеточкам (клеткам).

Какие есть формулы?

Есть способ, при котором надо воспользоваться формулой, основой которой будет понятие узла, узла внутреннего и узла внешнего. Узел это пересечение линий, образующих эти самые клеточки. Внешние узлы, это узлы, находящиеся на сторонах и вершинах геометрических фигур, площади которых нам надо найти. А внутренние узлы, это узлы внутри этих фигур. Клеточки у нас со сторонами равными одному сантиметру (1 см).

Формула, о которой идет речь, называется формула Пика.

Выглядит она вот так:

И по ней очень просто посчитать площадь фигуры S. В этой формуле M это количество внешних узлов, N – количество внутренних узлов.

Приведем пример, возьмем геометрическую фигуру параллелограмм:

Внутренние узлы – синие – N – их у нас 20.

Внешние узлы – красные – М – их у нас 18 и их количество нам надо поделить на два, получится 18/2 = 9 узлов.

Складываем 9 + 20 и вычитаем единицу: 20 + 9 – 1 = 28 см².

Еще один пример:

S = 14/2 + 43 – 1 = 49 см².

система выбрала этот ответ лучшим

Ксарфакс
[156K]

6 лет назад

Допустим, у нас есть произвольная фигура, построенная на листе в клетку. Необходимо вычислить её площадь.

Площадь фигуры по клеточкам

Для того, чтобы найти площадь любой фигуры по клеточкам, можно использовать формулу Пика.

Данная формула основана на подсчёте количества узлов, лежащих внутри фигуры и на её границе.

Узел – это точка, которая лежит на пересечении 2 линий данной сетки: вертикальных и горизонтальных.

Площадь фигуры по клеточкам находится по формуле:

N – количество узлов, которые находятся внутри фигуры.

M – количество узлов, которые находятся на границах (на вершинах и сторонах).

Примеры нахождения площади по клеточкам

1) Найдём площадь треугольника. Будем считать, что одна клетка – это 1 см.

Отметим внутренние узлы и узлы, которые находятся на границах.

N = 7 (внутренние).

M = 8 (узлы на границах).

Площадь треугольника S = 7 + 8/2 – 1 = 10 см².

2) Найдём площадь трапеции по клеточкам, одна клетка – это 1 см. Отметим все узлы и подсчитаем их количество.

N = 11 (внутренние).

M = 12 (узлы на границах).

Площадь трапеции S = 11 + 12/2 – 1 = 16 см².

3) Найдём площадь произвольного многоугольника. Одна клетка – это 1 см.

Отметим внутренние узлы и узлы, расположенные на границах фигуры. Подсчитаем их количество.

N = 6 (внутренние узлы).

M = 8 (узлы на границах).

Площадь многоугольника S = 6 + 10/2 – 1 = 10 см².

Марина Вологда
[295K]

3 года назад

Такие задачи очень часто встречаются, когда известен размер клеточки и дана фигура.

Вот пример таких задач:

Решение зависит от того, какая фигура дана и как именно она размещена относительно клеточек.

Возьмем простой пример, необходимо вычислить площадь вот такого треугольника:

Вспоминаем правило:

Теперь считаем, сколько клеточек треугольник в длину и сколько в высоту. У нас получается 2 в высоту и 6 в длину.

Подставляем к формуле:

S = 1/2 х 2 х 6 = 6 см2.

Считаем по клеточкам, подставляя формулу Пика:

Целых клеточек у нас 3.

Теперь считаем, сколько не целых: 6. Делим их на 2.

S = 3 + 6:2 = 6 см2.

А теперь высчитываем по формуле Пика: количество узлов сетки внутри – 2, количество узлов сетки, лежащих на границах – 10.

Подставляем к формуле и получаем – 2 + 10:2 – 1 = 6 см2.

Теперь давайте рассмотрим вот такой треугольник:

Чтобы найти площадь, вспоминаем правило:

Считаем клеточки и подставляем в формулу:

S = 1/2 х 2 х 6 = 6 см2.

А теперь находим по клеточкам: целых клеточек 2, не целых клеточек 8. Подставляем в формулу: 2 + 8:2 = 6 см2.

Пробуем сделать по формуле Пика: количество узлов сетки внутри – 3, количество узлов сетки, лежащих на границах – 8.

Подставляем к формуле и получаем – 3 + 8:2 – 1 = 6 см2.

Enot-Nina
[110K]

3 года назад

Найти площадь геометрической фигуры можно самыми разными способами:

Самый простой вариант – это вручную посчитать клеточки – целые и половинки также поскладывать. Простой, хотя и не самый быстрый и может не самый точный способ, но он работает. Чтобы легче было считать, достаточно расчертить фигуру на более простые.

Есть еще один способ – это использовать давно разработанную формулу. Это так называемая формула Пика. Для нее нужно посчитать количество узлов – точек пересечения клеточек, что окружены фигурой (находятся внутри нее), а также подсчитать количество пограничных узлов – по контуру фигуры.

Вот на картинке наглядно показано, как ее можно применять, чтоб посчитать площадь любой фигуры по клеточкам:

Бархатные лапки
[382K]

3 года назад

Площадь любого многоугольника можно посчитать по клеточкам. Для этого применяем формулу Пика. На нашем рисунке В – количество узловых клеточек внутри фигуры, Г – количество узлов на границе . Узлы – пересечение двух линий. многоугольника. Площадь равна S = В + Г/2 – 1 Считаем точки на рисунке и подставляем в формулу. – 10 + 7/2 -1 = 12,5.

Таким образом можно посчитать площадь, если вершины фигуры лежат в узлах.

Ann Luka
[2.8K]

6 лет назад

Чтобы найти площадь фигуры по клеточкам, нужно посчитать сколько в фигуре целых клеточек. Потом нужно посчитать сколько не целых и поделить их количество на 2. Добавить к получившемуся числу количество целых клеточек – это и будет правильный ответ.

Например. В треугольнике 3 целых клетки и 4 не целых. 3+4/2=5 пощадь треугольника 5 клеток.

Outline
[18.3K]

3 года назад

Для того, чтобы определить площадь фигуры на бумаге в клеточку есть универсальная формула Пика, позволяющая вычислить площадь изображения, но в только в том случае, если вершины искомой фигуры имеют целые (натуральные числа) координаты. Называется эта формула, в честь Георга Пика:

S=В + Г / 2 − 1

В этой формуле буквенные обозначения означают следующее:

В — количество целочисленных точек внутри многоугольника;

Г — количество целочисленных точек на границе (вершинах и сторонах) многоугольника;

S – площадь фигуры.

Здесь используется понятие “целочисленные” – это те, точки, которые расположены на пересечениях сетки (в ее узлах).

Для примера, найдем площадь треугольника:

Обозначим внутренние точки нашей фигуры красными кружками, а те, что на границах – синим цветом. Считаем красные и синие точки:

В=12, Г=4.

Исходя из подсчетов определяем площадь треугольника по формуле:

S=В+Г/2-1=12+2-1=13.

Можно убедиться в правильность проведенных выше расчетах. Рассчитываем площадь квадрата, обведенного красным, и вычитаем площади зеленого, синего и фиолетового треугольников:

S квадрата равна 36, площади треугольников: синего – 6, зеленого – 2, фиолетового – 15.

Исходя из полученных данных, S белого треугольника равна 13:

S=36-6-15-2=13.

KritikSPb
[93.7K]

3 года назад

Подсчет клеточек – дело полезное. С их помощью можно найти площадь геометрической фигуры.

Достаточно воспользоваться формулой, доказанной Георгом Пиком в 1899 году.

Подходит для расчета площади фигур с прямыми сторонами и целым количеством углов, чаще всего применяют для нахождения площади разносторонних треугольников и многоугольников с числом углов больше 4-х.

На теорему Пика есть задания в ЕГЭ.

127771
[272K]

3 года назад

Сначала я подумал, что нужно будет фигуру, которая указана на рисунке в клеточку разбить по фигурам так, чтобы можно посчитать площадь каждой фигуры по-отдельности, но оказалось все намного проще. Существует для данной задачи специальная формула Пика, которая выглядит следующим образом:

Площадь = В + Г/2 – 1, где:

В – количество целочисленных точек внутри многоугольника.
Г – количество целочисленных точек на границе многоугольника.

Теперь разберемся на примере, у нас есть такой пример:

Перед нами трапеция. Допустим площадь одной клетки 1 кв.см. Теперь можно воспользоваться формулой:

11+12/2-1=16 кв.см.

Бекки Шарп
[71.2K]

3 года назад

Найти площадь фигуры можно если вершины фигуры находятся в уголках клеточек, так называемые Целочисленные вершины или узловые точки. Решать задачу будем по формуле Пика, где

В – количество внутренних узловых точек,
Г – количество граничных узловых точек,

Вот такая фигура у нас –

Считаем точки и подставляем в формулу: S = 17 + 14/2 – 1 = 23

Ответ мы получаем в квадратных единицах, то есть клеточках.

Знаете ответ?

Источник

Задание 1

Задание 2

Задание 3

Задание 4

Задание 5

Площадь треугольника, изображённого на клетчатой бумаге

Геометрия. Урок 1. Задания. Часть 2.

Решение №2287 На клетчатой бумаге с размером клетки 1×1 изображён треугольник.

Вам также может понравиться

Как найти давление газа внутри сосуда

Как найти квесты в обливионе

Как найти поставщиков книг

Добавить комментарий Отменить ответ