|
В таком виде вопроса , ответа на задание не существует. Представьте треугольник который нарисован на листе бумаги или , треугольник образованный тремя городами на карте. Площадь таких фигур будет отличатся в десятки тысяч раз. Необходимо знать размеры сторон фигуры. В этом случае площадь высчитывается по математической формуле Герона. автор вопроса выбрал этот ответ лучшим Владислав Ч 8 лет назад Нельзя найти площадь треугольника только через периметр. Формула Герона требует знания ещё и каждой из 3-хсторон. Саму формулу см. в ответе Rafail [20.9K] на Ваш вопрос. Oleg74 8 лет назад Чтобы найти площадь треугольника, если известен только периметр, то такую площадь найти будет очень сложно, если невозможно. Если треугольник равносторонний, то стороны треугольника по известному периметру можно будет найти , если периметр разделить на 3, а если треугольник – не равносторонний, то тогда тупик, так как в нахождении площади треугольника применяется формула Герона, в которой нужно знать длины всех трех сторон. Формула Герона : Ksyusha26 8 лет назад Это вполне возможно. Только для этого нужно знать три стороны треугольника. Если известны все три стороны (a,b,c), то тогда используем формулу Герона. Сначала только найдем периметр (p). Извлекаем корень квадратный из числа, которое мы получим следующим выражением: p (p-a)(p-b)(p-c). Вот и все Знаете ответ? |
Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона
Формула Герона для нахождения площади треугольника:
Через основание и высоту
Формула нахождения площади треугольника с помощью половины его основания и высоту:
Через две стороны и угол
Формула нахождения площади треугольника через две стороны и угол между ними:
Через сторону и два прилежащих угла
Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
Площадь прямоугольного треугольника
Прямоугольный треугольник – треугольник у которого один из углов прямой, т.е. равен 90°.
Формула нахождения площади прямоугольного треугольника через катеты:
Площадь равнобедренного треугольника через стороны
Равнобедренный треугольник – треугольник, в котором две стороны равны. А значит, равны и два угла.
Формула нахождения площади равнобедренного треугольника через две стороны:
Площадь равнобедренного треугольника через основание и угол
Формула нахождения площади равнобедренного треугольника через основание и угол:
Площадь равностороннего треугольника через стороны
Равносторонний треугольник – треугольник, в котором все стороны равны, а каждый угол равен 60°.
Формула нахождения площади равностороннего треугольника через сторону:
Площадь равностороннего треугольника через высоту
Формула нахождения площади равностороннего треугольника через высоту:
Площадь равностороннего треугольника через радиус вписанной окружности
Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
Площадь равностороннего треугольника через радиус описанной окружности
Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
Площадь треугольника через радиус описанной окружности и три стороны
Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
Площадь треугольника через радиус вписанной окружности и три стороны
Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
Площадь треугольника
Определение площади треугольника
Площадь треугольника — это величина, которая
показывает какие размеры у треугольника.
Сейчас, на примере покажем, что такое площадь,
а также, как можно найти площадь треугольника.
Площадь треугольника, можно очень легко объяснить
на примере прямоугольного треугольника в клеточном поле.
Площадь, в нашем случае, будет равна количеству клеток.
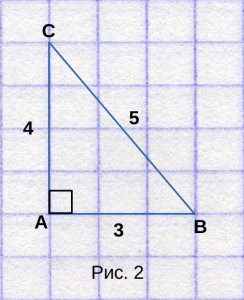
Для наглядности, нарисуем прямоугольный треугольник
ABC, со длинами сторон 3, 4 и 5, как на рисунке 2. Отметим, что он прямоугольный.
Посчитаем количество клеток, которые занимает треугольник.
3 полных клетки, и 4 неполных клетки, но для того, чтобы узнать
площадь треугольника в клеточном поле нам нужно узнать количество
полных клеток, которые занимает весь треугольник. Наша задача в том,
чтобы неполные клетки преобразовать в полные.
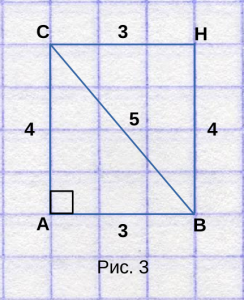
Для этого нарисуем второй треугольник, так,
чтобы получился прямоугольник, как на рисунке 3.
Как видим, весь прямоугольник занимает 12 полных клеток.
Формула площади прямоугольника равна произведению
одной стороны на другую — ( S = ab ) ,
поэтому площадь прямоугольника равна 3 * 4 = 12 клеткам.
Площадь треугольника, из которого состоит прямоугольник,
можно найти по другой формуле: ( S = frac<1>2 ab ) .
Подставив значения длин сторон, получаем — S = 0.5 * 3 * 4,
из чего следует, что S = 6 клетками, или же квадратным сантиметрам.
Прямоугольник можно условно разделить
на два треугольника, поэтому площадь треугольника
равна половине площади прямоугольника.
Формула площади треугольника — это формула,
по которой можно найти площадь треугольника.
Формулы площади треугольника применяют, только,
и только тогда, когда невозможно узнать площадь
треугольника, глядя на рисунок, или просто посчитав клетки.
Формулы площади треугольника
Ⅰ. Через высоту и основание
a — сторона, на которую падает высота,
b — высота.
Самая известная формула площади треугольника.
Зная только высоту и сторону, на которую падает
эта высота, можно найти площадь треугольника.
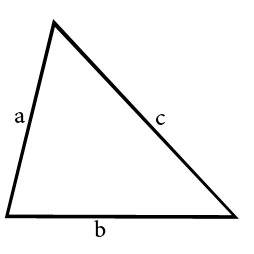
Ⅱ. Через все стороны и периметр
p — полупериметр, вычисляется по формуле: ( p = frac <2>) ,
a, b, c — стороны треугольника.
Это формулу, нужно использовать когда известны
все три стороны треугольника. Зная три стороны
треугольника можно найти периметр, а дальше
найти и площадь заданного треугольника.
Эту формулу площади также называют формулой Герона.
Ⅲ. Через две стороны и угол между ними
[ S = frac<1> <2>a cdot b cdot sin β ]
a, b — стороны между которыми расположен угол β,
sin β — синус угла β.
Формула применяется, когда известен
один из углов, и две стороны, образующие
этот угол. В некоторых задачах площадь
треугольника можно найти только по этой формуле.
Ⅳ. Через периметр и радиус вписанной окружности
[ S = r cdot frac
2 ]
r — радиус вписанной окружности,
P — периметр треугольника.
Тут даже не обязательно знать все стороны треугольника,
достаточно знать периметр и радиус описанной окружности.
Ⅴ. Через все стороны и радиус описанной окружности
abc — произведение всех сторон треугольника,
R — радиус описанной окружности.
Пожалуй, единственная формула, где площадь
треугольника можно найти только через радиус
описанной окружности и произведение трех сторон.
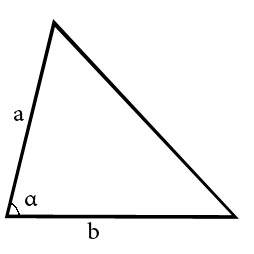
Ⅵ. Через сторону и два прилежащих к ней угла
a — сторона треугольника,
sin α — синус угла α,
sin β — синус угла β.
Готов поспорить, вы даже ни разу не видели этой формулы.
Эта очередная формула площади треугольника, применяется
в крайне редких случаях — когда известны два угла и сторона,
к которой эти углы примыкают.
Как найти площадь треугольника – все способы от самых простых до самых сложных
Зависит от того, какой треугольник.
Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.
Если треугольник прямоугольный
То есть один из его углов равен 90 градусам.
Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.
Если он равнобедренный
То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.
Если он равносторонний
То есть все три стороны равны. Ваши действия такие:
- Найдите квадрат стороны – умножьте эту сторону на нее же. Если у вас сторона равна 4, умножьте 4 на 4, будет 16.
- Умножьте полученное значение на корень из 3. Это примерно 1,732050807568877293527.
- Поделите все на 4.
Если известна сторона и высота
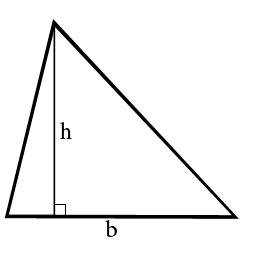
Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.
Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.
Если известны две стороны и градус угла между ними
Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:
Если известны длины трех сторон
- Найдите периметр. Для этого сложите все три стороны.
- Найдите полупериметр – разделите периметр на два. Запомните значение.
- Отнимите от полупериметра длину первой стороны. Запомните.
- Отнимите от полупериметра длину второй стороны. Тоже запомните.
- Отнимите от полупериметра длину третьей стороны. И ее запомните.
- Умножьте полупериметр на каждое из этих чисел (разницу с первой, второй и третьей стороной).
- Найдите квадратный корень.
Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.
Если известны три стороны и радиус описанной окружности
Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.
Если известны три стороны и радиус вписанной окружности
Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.
Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.
Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.
[spoiler title=”источники:”]
http://colibrus.ru/ploschad-treugolnika/
http://vsvoemdome.ru/obrazovanie/kak-nayti-ploschad-treugolnika
[/spoiler]
Основные понятия
Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
Площадь — это численная характеристика, которая дает нам информацию о размере части плоскости, ограниченной замкнутой геометрической фигурой.
Популярные единицы измерения площади:
-
квадратный миллиметр (мм2);
-
квадратный сантиметр (см2);
-
квадратный дециметр (дм2);
-
квадратный метр (м2);
-
квадратный километр (км2);
-
гектар (га).
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас
Формула площади треугольника
Для решения задач применяются различные формулы, в зависимости от известных исходных данных. Далее мы рассмотрим способы решения для всех типов треугольников, в том числе частные случаи для равносторонних, равнобедренных и прямоугольных фигур.
Быстро вычислить площадь треугольника поможет наш онлайн-калькулятор. Просто введите известные вам значения и получите ответ в метрах, сантиметрах или миллиметрах.
Пройдите тест и узнайте, какие темы отделяют от пятёрки по математике
Добро пожаловать в школу магии.
О нет! Мальчик-молния случайно попал в школьные часы. Теперь они отстают. Мы все можем задержаться в школе
Жми на стрелки сверху, чтобы путешествовать в истории→
Одна ученица когда-то была в школьной кладовке и видела там схему часов
Но в кладовку просто так не попадёшь→
Реши два примера от волшебной статуи на входе в кладовку
frac{1}{7} + frac{3}{7} =
frac{4}{7}
frac{5}{7}
frac{4}{14}
frac{2}{7}
frac{4}{15} – frac{1}{15} =
frac{1}{3}
frac{1}{5}
frac{3}{30}
frac{1}{10}
Схема у нас!
Деталь можно сделать из проволоки и формы для заливки металла. Найди их на картинке
Теперь осталось взять инструменты у садовника! Он обменяет их на волшебные бобы для его сада
Для починки часов нужны: молоток, отвертка и плоскогубцы.
Ты можешь либо одолжить у садовника набор, либо отдельные инструменты, либо и то, и другое. Какое минимальное количество волшебных бобов ты можешь отдать садовнику?
Ответ:
562 боба
400 бобов
553 боба
Деталь имеет форму прямоугольника со сторонами 5 см и 12 см. Найди периметр и площадь детали, чтобы посчитать, сколько проволоки для неё понадобится
Периметр прямоугольника равен
40 см
26 см
22 см
34 см
Площадь прямоугольника равна
50 см^2
46 см^2
60 см^2
62 см^2
Мальчик-молния выплавил деталь, часы должны работать! Но они почему-то не идут… Кажется, одной шестерёнки не хватает — она куда-то упала
В коробке, шкатулке, ящике и банке находятся пыльца, волчий корень, золото и шестерёнка. Шестерёнка и пыльца не в коробке, ёмкость с волчьим корнем стоит между ящиком и ёмкостью с золотом, в банке не волчий корень и не шестерёнка. Шкатулка стоит около банки и ёмкостью с пыльцой. В какой ёмкости что находится?
Соедини ёмкости с содержимым на картинках ниже
Шестерёнка
Золото
Волчий корень
Пыльца
Ура, мы вставили последнюю шестеренку, и часы пошли! Сегодня уроки закончатся вовремя. Спасибо тебе за помощь!
Дальше узнаешь свои результаты →
Формулы площади для любого треугольника
1. Площадь треугольника через основание и высоту
, где
— основание,
— высота.
2. Площадь треугольника через две стороны и угол между ними.
, где
,
— стороны,
— угол между ними.
3. Площадь треугольника через описанную окружность и стороны
, где
,
,
— стороны,
— радиус описанной окружности.
4. Площадь треугольника через вписанную окружность и стороны.
, где
,
,
— стороны,
— радиус вписанной окружности.
, где
— полупериметр.
5. Площадь треугольника по стороне и двум прилежащим углам
, где
— сторона,
и
— прилежащие углы.
6. Формула Герона для вычисления площади треугольника
Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.
, где
,
,
— стороны,
— полупериметр, который можно найти по формуле:
Для прямоугольного треугольника
Для прямоугольного треугольника чаще всего используют одну формулу — половину произведения катетов. Потому что их всегда можно найти с помощью правил тригонометрии или теоремы Пифагора.
, где
,
— стороны.
Площадь треугольника по гипотенузе и острому углу
, где
— гипотенуза,
— любой из прилегающих острых углов.
Гипотенузой принято называть сторону, которая лежит напротив прямого угла.
Площадь прямоугольного треугольника по катету и прилежащему углу
, где
— катет,
— прилежащий угол.
Катетом принято называть одну из двух сторон, образующих прямой угол.
Площадь треугольника через гипотенузу и радиус вписанной окружности
, где
— гипотенуза,
— радиус вписанной окружности.
Площадь треугольника по отрезкам, на которые делит вписанная окружность его гипотенузу
, где
,
— части гипотенузы.
Площадь прямоугольного треугольника по формуле Герона
, где
,
— катеты,
— полупериметр, который можно найти по формуле:
Для равнобедренного треугольника
Ниже мы покажем разные формулы для площади равнобедренного и равностороннего треугольника, их редко используют, но их легко вывести самому. Попробуйте сделать это самостоятельно.
Вычисление площади через основание и высоту
, где
— основание,
— высота, проведенная к основанию.
Поиск площади через боковые стороны и угол между ними.
, где
— боковая сторона,
— угол между боковыми сторонами.
Площадь равностороннего треугольника через радиус описанной окружности
, где
— радиус описанной окружности.
Площадь равностороннего треугольника через радиус вписанной окружности
, где
— радиус вписанной окружности.
Площадь равностороннего треугольника через сторону
, где
— сторона.
Площадь равностороннего треугольника через высоту
, где
— высота.
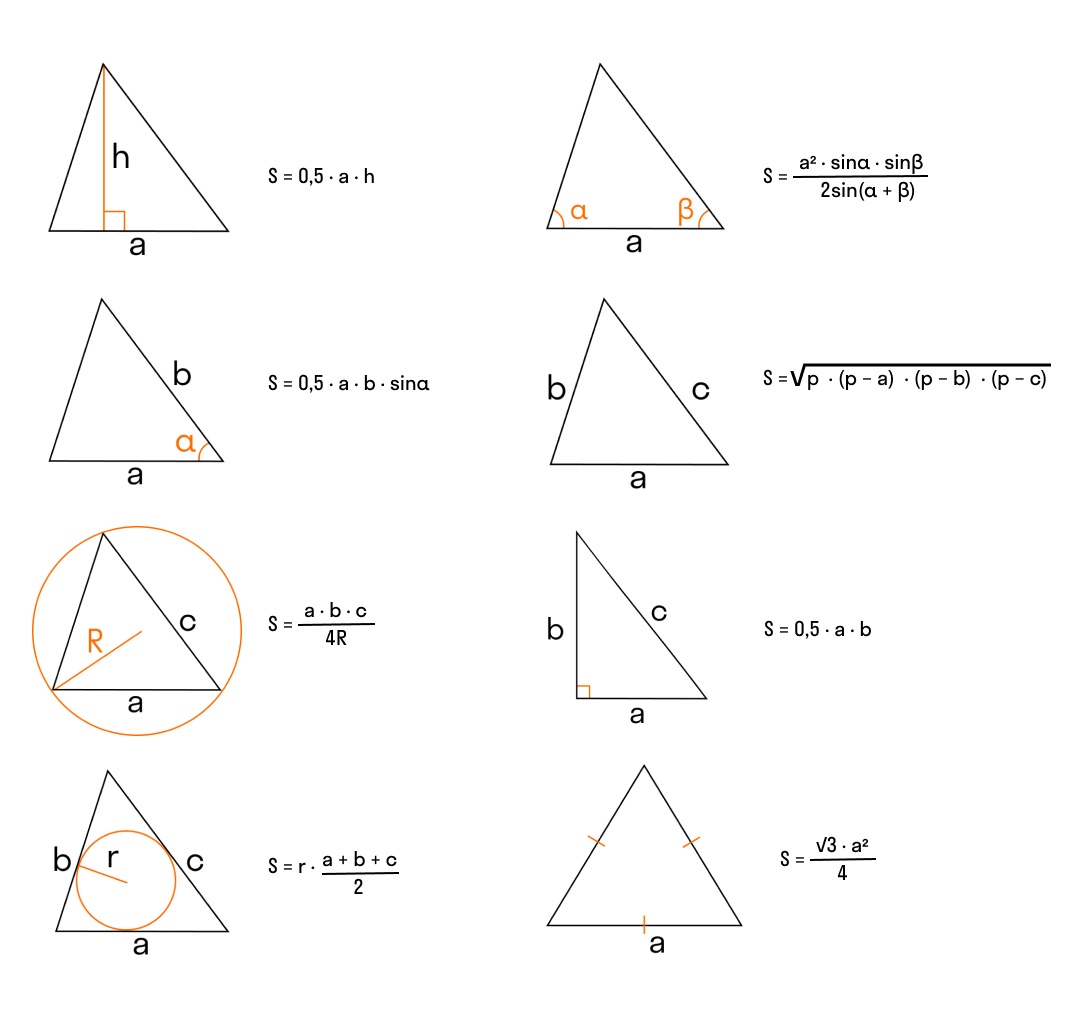
Таблица формул нахождения площади треугольника
В задачах встречаются разные фигуры, и кажется, что нужны разные формулы. Но на самом деле, зная всего несколько формул для треугольника и пользуясь теоремами и свойствами геометрии, можно найти площадь любой фигуры.
Скачать таблицу
Но что делать, если нужно решить контрольную по математике или геометрии быстро, а вы плохо знаете конкретную тему? Закажите контрольную по математике онлайн у специалистов, которые помогут быстро выполнить задание и пояснят решение.

Формула:
S
=
1
2
ab
·
sin(α)
Где: a, b – катеты, c – гипотенуза.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
abc
4R
Где: a, b, c – стороны разностороннего треугольника, R – радиус описанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
abc
2D
Где: a, b, c – стороны разностороннего треугольника, D – диаметр описанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано
Формула:
S
=
a
b
c
4
S
π
Где: a, b, c – стороны разностороннего треугольника, S – площадь описанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
π
a
b
c
2P
Где: a, b, c – стороны разностороннего треугольника, P – длина описанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
R
·
a
+
b
+
c
2
Где: a, b, c – стороны разностороннего треугольника, R – радиус вписанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
D
·
a
+
b
+
c
4
Где: a, b, c – стороны разностороннего треугольника, D – диаметр вписанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
SO
π
·
a
+
b
+
c
2
Где: a, b, c – стороны разностороннего треугольника, SO – площадь вписанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
P
π
·
a
+
b
+
c
4
Где: a, b, c – стороны разностороннего треугольника, P – длина вписанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
a2
2
·
sin(α)
·
sin(β)
sin(180-(α+β))
Где: a – сторона, α, β – прилегающие углы.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
p(p-a)(p-b)(p-c)
p
=
a
+
b
+
c
2
Где: a, b, c – стороны, p – половина периметра.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано
Площадь треугольника равна произведению длины вписанной окружности поделенной на пи и четверти периметра треугольника.
Онлайн калькулятор площади треугольника. Как узнать площадь треугольника.
При помощи нашего калькулятора вы легко сможете узнать площадь треугольника.
|
|
|
| Вычислить площадъ треугольника через: | |
| Высота треугольника h: | |
| Длина стороны b: |
Существует несколько формул при помощи которых можно вычислить площадь треугольника.
- Мы можем вычислить площадь треугольника зная его высоту и длину основания по следующей формуле:
S=1/2bh
- Так же площадь треугольника можно узнать используя формулу Герона, по которой можно вычислить площадь зная периметр или длину всех сторон треугольника:
S= √p(p-a)(p-b)(p-c)
где p – это полупериметр треугольника
- Еще мы можем узнать площадь треугольника зная длину двух сторон и угол между ними
S=1/2ab sin(α)