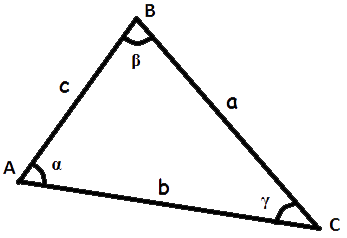Как найти площадь треугольника по теореме герона

Как найти площадь треугольника по теореме герона

Фо́рмула Герона — формула для вычисления площади треугольника S по длинам его сторон a,b,c:

{displaystyle S={sqrt {p(p-a)(p-b)(p-c)}}},

где p — полупериметр треугольника: {displaystyle p={tfrac {1}{2}}cdot (a+b+c)}.

Формула содержится в «Метрике» Герона Александрийского (I век н. э.) и названа в его честь (хотя она была известна ещё Архимеду). Герон интересовался треугольниками с целочисленными сторонами, площади которых тоже являются целыми, такие треугольники носят название героновых, простейшим героновым треугольником является египетский треугольник.

Доказательство 1 (тригонометрическое):

Доказательство 2 (на основе теоремы Пифагора):

Треугольник со сторонами a, b, c и высотой

h, разделяющей основание

c на

d и (c − d).

По теореме Пифагора имеем следующие равенства для гипотенуз: a2 = h2 + (c − d)2 и b2 = h2 + d2 — см. рисунок справа. Вычитая из первого равенства второе, получаем a2 − b2 = c2 − 2cd. Это уравнение позволяет нам выразить d через стороны треугольника:

{displaystyle d={frac {-a^{2}+b^{2}+c^{2}}{2c}}}

Для высоты h у нас было равенство h2 = b2 − d2, в которое можно подставить полученное выражение для d и применить формулы для квадратов:

{displaystyle {begin{aligned}h^{2}&=b^{2}-left({frac {-a^{2}+b^{2}+c^{2}}{2c}}right)^{2}={frac {(2bc-a^{2}+b^{2}+c^{2})(2bc+a^{2}-b^{2}-c^{2})}{4c^{2}}}\&={frac {((b+c)^{2}-a^{2})(a^{2}-(b-c)^{2})}{4c^{2}}}={frac {(b+c-a)(b+c+a)(a+b-c)(a-b+c)}{4c^{2}}}\end{aligned}}}

Замечая, что {displaystyle b+c-a=2p-2a}, a+b+c=2p, a+b-c=2p-2c, {displaystyle a-b+c=2p-2b}, получаем:

{displaystyle {begin{aligned}h^{2}&={frac {2(p-a)cdot 2pcdot 2(p-c)cdot 2(p-b)}{4c^{2}}}={frac {4p(p-a)(p-b)(p-c)}{c^{2}}}end{aligned}}}

Используя основное равенство для площади треугольника {displaystyle S={frac {ch}{2}}} и подставляя в него полученное выражение для h, в итоге имеем:

{displaystyle {begin{aligned}S={sqrt {{frac {c^{2}}{4}}cdot {frac {4p(p-a)(p-b)(p-c)}{c^{2}}}}}={sqrt {p(p-a)(p-b)(p-c)}}end{aligned}}}

ч.т.д.

Вариации и обобщения[править | править код]

  • Формулу Герона можно записать с помощью определителя в виде[1]:
    -16S^{2}={begin{vmatrix}0&a^{2}&b^{2}&1\a^{2}&0&c^{2}&1\b^{2}&c^{2}&0&1\1&1&1&0end{vmatrix}}={begin{vmatrix}a&b&c&0\b&a&0&c\c&0&a&b\0&c&b&aend{vmatrix}}
Первый определитель последней формулы является частным случаем определителя Кэли — Менгера[en] для вычисления гиперобъёма симплекса.
через длины высот h_{a}, h_{b} и h_{c} и полусумму их обратных величин H=(h_{a}^{-1}+h_{b}^{-1}+h_{c}^{-1})/2[3]:

S^{-1}=4{sqrt {H(H-h_{a}^{-1})(H-h_{b}^{-1})(H-h_{c}^{-1})}};
через углы треугольника alpha , beta и gamma , полусумму их синусов {displaystyle s=(sin alpha +sin beta +sin gamma )/2} и диаметр описанной окружности {displaystyle D={tfrac {a}{sin alpha }}={tfrac {b}{sin beta }}={tfrac {c}{sin gamma }}}[4]:

S=D^{2}{sqrt {s(s-sin alpha )(s-sin beta )(s-sin gamma )}}.
  • Площадь вписанного в окружность четырёхугольника вычисляется по формуле Брахмагупты:
    S={sqrt {(p-a)(p-b)(p-c)(p-d)}},
где p={frac {a+b+c+d}{2}} — полупериметр четырёхугольника; в данном случае треугольник оказывается предельным случаем вписанного четырёхугольника при устремлении длины одной из сторон к нулю. Та же формула Брахмагупты через определитель[5]:

S={frac {1}{4}}{sqrt {-{begin{vmatrix}a&b&c&-d\b&a&-d&c\c&-d&a&b\-d&c&b&aend{vmatrix}}}}
где:

{displaystyle {begin{aligned}a&={sqrt {xYZ}}\b&={sqrt {yZX}}\c&={sqrt {zXY}}\d&={sqrt {xyz}}\X&=(w-U+v),(U+v+w)\x&=(U-v+w),(v-w+U)\Y&=(u-V+w),(V+w+u)\y&=(V-w+u),(w-u+V)\Z&=(v-W+u),(W+u+v)\z&=(W-u+v),(u-v+W)end{aligned}}}.
где theta _{s}={frac {theta _{a}+theta _{b}+theta _{c}}{2}} — полупериметр.

Примечания[править | править код]

  1. ↑ Weisstein, Eric W. Heron’s Formula. Архивная копия от 5 сентября 2015 на Wayback Machine From MathWorld–A Wolfram Web Resource.
  2. ↑ Benyi, Arpad, “A Heron-type formula for the triangle, « Mathematical Gazette» 87, July 2003, 324—326.
  3. ↑ Mitchell, Douglas W., “A Heron-type formula for the reciprocal area of a triangle, ” Mathematical Gazette 89, November 2005, 494.
  4. ↑ Mitchell, Douglas W., “A Heron-type area formula in terms of sines, ” Mathematical Gazette 93, March 2009, 108—109.
  5. ↑ Стариков В. Н. Заметки по геометрии// Научный поиск: гуманитарные и социально-экономические науки: сборник научных трудов. Выпуск 1/ Гл ред. Романова И .В Чебоксары: ЦДИП «INet», 2014. С. 37-39
  6. ↑ W. Kahan, «What has the Volume of a Tetrahedron to do with Computer Programming Languages?», [1] Архивная копия от 27 июня 2013 на Wayback Machine, pp. 16-17.
  7. ↑ Маркелов С. Формула для объёма тетраэдра// Математическое просвещение. Вып. 6. 2002. С. 132

Литература[править | править код]

  • § 258 в А. П. Киселёв, Геометрия по Киселёву, arΧiv:1806.06942 [math.HO].
  • Николаев Н. О площади треугольника // В.О.Ф.Э.М.. — 1890. — № 108. — С. 227—228.
  • Raifaizen, Claude H. A Simpler Proof of Heron’s Formula (англ.) // Mathematics Magazine : magazine. — 1971. — Vol. 44. — P. 27—28. — доказательство формулы Герона на основе теоремы Пифагора
Источник

В данной публикации мы рассмотрим формулу Герона, пользуясь которой можно найти площадь треугольника. Также разберем примеры решения задач для того, чтобы закрепить представленный материал.

  • Формула площади

  • Примеры задач

Формула площади

Площадь треугольника (S) равняется квадратному корню из произведения его полупериметра (p) на разности полупериметра и каждой из его сторон (a, b, c).

S = √p(p-a)(p-b)(p-c)

Формула Герона

Полупериметр (p) вычисляется таким образом:

Формула Герона

Примечание: для использования формулы необходимо знать/найти длину всех сторон треугольника.

Формула получила такое название в честь греческого математика и механика Герона Александрийского, который изучал треугольники с целочисленными сторонами и площадью (героновские). К таким, например, относится прямоугольный треугольник с соотношением сторон 3:4:5, который также называют египетским.

Египетский треугольник

Примеры задач

Задание 1
Найдите площадь треугольника со сторонами 6, 8 и 10 см.

Решение
Для начала найдем полупериметр:
p = (6 + 8 + 10) / 2 = 12 см.

Теперь воспользуемся формулой Герона, подставив в нее заданные значения:
S = √12(12 – 6)(12 – 8)(12 – 10) = √12 ⋅ 6 ⋅ 4 ⋅ 2 = 24 см2.

Задание 2
В прямоугольном треугольнике длина гипотенузы равняется 15 см, а одного из катетов – 9 см. Вычислите площадь фигуры.

Решение
Пусть гипотенуза – это c, известный катет – a, а неизвестный – b.

Применим Теорему Пифагора, чтобы найти длину катета b:
b2 = c2 – a2 = 152 – 92 = 144 см2, следовательно, b = 12 cм.

Полупериметр треугольника равен:
p = (9 + 12 + 15) / 2 = 18 см.

Остается только использовать формулу для нахождения площади:
S = √18(18 – 9)(18 – 12)(18 – 15) = √18 ⋅ 9 ⋅ 6 ⋅ 3 = 54 см2.

Источник

Содержание:

  • Формулировка теоремы Герона
  • Примеры решения задач

Формулировка теоремы Герона

Теорема

Площадь треугольника равна корню из произведения разностей полупериметра
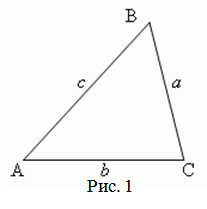
$p$ треугольника (рис 1) и каждой из его сторон $a$, $b$ и $c$ на полупериметр:

$S=sqrt{p(p-a)(p-b)(p-c)}$

где полупериметр

$$p=frac{a+b+c}{2}$$

Треугольник со сторонами $a$, $b$ и $c$.

Формула Герона позволяет вычислить площадь треугольника по известным длинам его сторон.

Эта формула содержится в “Метрике” греческого математика и механика Герона Александрийского и названа в его честь.
Герон интересовался треугольниками с целочисленными сторонами. Такие треугольники носят название героновых треугольников.
Простейшим героновым треугольником является египетский треугольник – прямоугольный треугольник со соотношениями сторон
$3 : 4 : 5$ .

Примеры решения задач

Пример

Задание. Вычислите площадь треугольника, зная, что его стороны равны 6 см; 5 см и 2,2 см.

Решение. Полупериметр

$$p=frac{6+5+2,2}{2}=6,6 (mathrm{см})$$

Тогда площадь треугольника, согласно формуле Герона, равна:

$$S=sqrt{6,6 cdot(6,6-6) cdot(6,6-5) cdot(6,6-2,2)}=$$

$$=sqrt{6,6 cdot 0,6 cdot 1,6 cdot 4,4}=sqrt{27,8784}=5,28left(mathrm{см}^{2}right)$$

Ответ. $S=5.28left(mathrm{см}^{2}right)$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Источник

Онлайн калькулятор. Площадь треугольника по трем сторонам. Формула Герона

Используя этот онлайн калькулятор, вы сможете найти площадь треугольника по трем сторонам используя формулу Герона.

Воспользовавшись онлайн калькулятором для вычисления площади треугольника, вы получите детальное пошаговое решение вашего примера, которое позволит понять алгоритм решения таких задач и закрепить пройденный материал.

Найти площадь треугольника по трем сторонам. Формула Герона.

Треугольник
Введите длины сторон треугольника:

a =   

b =   

c =   

Площадь в   

Вводить можно числа или дроби (-2.4, 5/7, …). Более подробно читайте в правилах ввода чисел.

Источник

Формула Герона

Формула Герона носит такое название в честь греческого математика и инженера Герона Александрийского. Он жил в I веке нашей эры. Герон занимался механикой, оптикой, геометрией и гидростатикой. Учёный интересовался треугольниками с целочисленными сторонами и целочисленными площадями. Такие фигуры получили название Героновых треугольников.

Формулировка теоремы Герона

Формула Герона – это арифметическая формула для вычисления площади треугольника по длинам его сторон. В таком случае площадь равна корню из произведения разностей полупериметра и каждой из его сторон.

Формула и доказательство

Формула Герона выглядит следующим образом:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

(S;=;sqrt{pleft(p-aright)left(p-bright)left(p-cright)})

где S – это площадь треугольника; a, b, c – это стороны треугольника; p – это полупериметр треугольника.

Чтобы вычислять полупериметр, нужно пользоваться формулой:

(p;=;frac{a+b+c}2)

Приведем доказательство.

Для этого рассмотрим треугольник ABC.

(left|ABright|=c,;left|BCright|=a,;left|ACright|=b)

CH – высота треугольника.

(left|CHright|=h,;left|AHright|=x,;left|BHright|=y)

Тогда (c=x+y).

По теореме Пифагора из треугольников ACH и BCH получаем:

(h^2=b^2-x^2=a^2-y^2)

Из этого:

(y^2-x^2=a^2-b^2)

((y-x)(y+x)=a^2-b^2)

(x+y=c)

Соответственно:

((y-x)c=a^2-b^2) и (y-x=frac1c (a^2-b^2))

Если сложить последнее равенство с (y+x=c), то получается

(y;=;frac{c^2+a^2-b^2}{2c})

Треугольник

 

Найдем высоту треугольника.

(h^2;=;a^2-y^2=left(a-yright)left(a+yright)=left(a-frac{c^2+a^2-b^2}{2c}right)left(a+frac{c^2+a^2-b^2}{2c}right)=frac{2ac-c^2-a^2+b^2}{2c}timesfrac{2ac+c^2+a^2-b^2}{2c}=frac{b^2-left(a-cright)^2}{2c}timesfrac{left(a+cright)^2-b^2}{2c}=frac{left(b-a+cright)timesleft(b+a-cright)}{2c}timesfrac{left(a+c-bright)timesleft(a+c+bright)}{2c})

Так как (p=frac12left(a+b+cright)), то ( b+c=2p-a),( a+b=2p-c), (a+c=2p-b), (a+b+c=2p).

С помощью этих равенств найдем высоту.

(h^2=frac{left(2p-2aright)left(2p-2cright)left(2p-2bright)2p}{4c^2}=frac{4pleft(p-aright)left(p-cright)left(p-bright)}{c^2})

А так как (S=frac12ch), то теорема доказана.

Для каких треугольников действует теорема

Применение формулы Герона допустимо для треугольников, у которых известны длины всех их сторон.

Примеры решения задач

Задача 1

Рассчитать площадь треугольника, если a=6, b=8, c=6.

Решение

(p=frac{6+8+6}2=10)

Тогда площадь треугольника равна:

(S=10sqrt{left(10-6right)left(10-8right)left(10-6right)}=320)

Ответ: 320 см2.

Задача 2

Вычислить площадь параллелограмма, если одна из его сторон равна 51, а диагонали равны 40 и 74.

Решение

Диагонали AC и BD  пересекаются в точке O.

Если  AD = 51,  AC = 40  и  BD = 74,  то  AO = 20,  OD = 37.

По формуле Герона:

(S_{ABCD} = 4S_{AOD} = sqrt{54left(54-51right)left(54-37right)left(54-20right)}=1224)

Ответ: 1224 см2. 

Задача 3

В треугольнике ABC три стороны:  AB = 26,  BC = 30  и  AC = 28. Найти часть площади этого треугольника, заключённую между высотой и биссектрисой, проведёнными из вершины B.

Решение

Задача 3

 

BP и BQ – высота и биссектриса треугольника.

По формуле Герона:

(S=sqrt{42left(42-30right)left(42-28right)left(42-26right)}=336)

(S = ½ AC·BP)

Поэтому  (BP =frac{2S}{AC}=frac{2times336}{28}=24).

По свойству биссектрисы треугольника:

(frac{AQ}{QC}=frac{AB}{BC}=frac{26}{30}=frac{13}{15})

Соответственно (AQ=frac{13}{28}AC = 13).

По теореме Пифагора из треугольника APB получаем:

(AP=sqrt{AP^2-BP^2}=sqrt{26^2-24^2}=sqrt{2times50}=10)

Следовательно,  (PQ = AQ – AP = 13 – 10 = 3)

(S_{BPQ} = ½ PQ·BP = frac{3times24}2=36)

Ответ: 36 см2.

Источник

Добавить комментарий