Как найти площадь треугольника по точкам внутри

Как найти площадь треугольника по координатам его вершин?

1способ:

Найти длины трёх сторон треугольника и вычислить площадь по формуле Герона. Способ удобен, если длины сторон являются целыми числами. В противном случае предстоят громоздкие вычисления.

2 способ:

вывести формулу для нахождения площади и использовать её для вычисления.

Утверждение

Площадь треугольника ABC с вершинами в точках A(x₁;y₁), B(x₂;y₂), C(x₃;y₃) можно вычислить с помощью формулы

   

Доказательство:

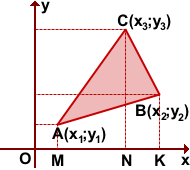Рассмотрим треугольник ABC,

A(x₁;y₁), B(x₂;y₂), C(x₃;y₃)

Опустим перпендикуляры из вершин треугольника на координатные оси.

   

   

   

   

   

   

   

   

   

   

   

   

   

С учетом вариантов взаимного расположения точек A, B и C формула для вычисления площади треугольника по координатам его вершин приобретает вид:

   

Что и требовалось доказать.

3 способ:

Найти длины двух сторон и косинус угла между ними и вычислить площадь треугольника через стороны и синус угла между ними.

4 способ:

Найти длину и уравнение одной стороны треугольника и длину высоты, проведённой к этой стороне. Вычислить площадь через сторону и высоту.

Рассмотрим эти способы на конкретном примере.

Найти площадь треугольника, вершины которого имеют координаты A(-1;-3), B(3;4), C(5;-5).

1 способ:

Находим длины сторон треугольника ABC.

   

   

   

   

   

   

Поскольку длины сторон выражены иррациональными числами, вычислять площадь треугольника по формуле Герона — не самый лучший способ.

2 способ:

Подставляем в формулу x₁=-1, y₁=-3, x₂=3, y₂=4, x₃=5, y₃=-5:

   

   

3 способ:

Угол A образован векторами AC и AB. Отсюда

   

Находим координаты векторов:

   

   

   

   

   

   

Скалярное произведение

   

Длины AB и AC уже знаем:

   

   

   

Синус и косинус одного угла связаны соотношением:

   

Синус угла от 0° до 180° является положительным числом, поэтому

   

   

Отсюда

   

   

4 способ:

Найдём уравнение прямой AB. Подставляем координаты A и B в уравнение y=kx+b:

   

Отсюда k=7/4, b=-5/4

   

   

Найдём расстояние от точки C до прямой AB:

   

Это расстояние равно высоте треугольника, проведённой из вершины C к стороне AB. Отсюда

   

Через точку, лежащую внутри треугольника, проведены три прямые, параллельные его сторонам. Эти прямые разделяют треугольник

Ваш ответ

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,688
• разное 16,822

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Через точку внутри треугольника проведены прямые параллельные сторонам найти площадь треугольника

• 

§2. Площадь треугольника. Метод площадей

В школьном курсе геометрии доказано несколько формул площади треугольника. Напомним их.

Пусть `A`, `B` и `C` – углы треугольника`ABC`; `a`, `b` и `c` – противолежащие этим углам стороны; `h_a`, `h_b` и `h_c` – высоты к этим сторонам; `r` – радиус вписанной окружности;`R` – радиус описанной окружности; `2p=(a+b+c)` – периметр треугольника; `S` – площадь треугольника

`S=1/2ah_a=1/2bh_b=1/2ch_c`,	(1)
`S=1/2 ab sinC=1/2acsinB=1/2bcsinA`,	(2)
`S=pr`,	(3)
``S=sqrt(p(p-a)(p-b)(p-c))` – формула Герона,	(4)
`S=(abc)/(4R)`.	(5)

При вычислении площади из этих формул следует выбрать ту, которая в условиях конкретной задачи приводит к более простому решению.

Для примера, рассмотрим два треугольника:

`DeltaABC:` `AB=13`, `BC=14`, `AC=15`;

`DeltaKML:` `KL=sqrt(13)`, `LM=sqrt(14)`, `KM=sqrt(15)`;

Надо найти площадь и радиус описанной окружности.

Для треугольника `ABC` удобен ход решения такой:

`p=1/2(AB+BC+AC)=21`, по формуле Герона

`S_(ABC)=sqrt(21*6*7*8)= ul(84)` и по формуле (5)

Для треугольника `KLM` вычисленная по формуле Герона затруднительны, более простой путь – найти косинус, например, угла `M`. По теореме косинусов

тогда `sinM=sqrt(1-64/(210))=(sqrt(146))/(sqrt(14)*sqrt(15))` и по формуле (2):

тогда `R=(KL)/(2sinM)=ul((sqrt(13)*sqrt(14)*sqrt(15))/(2*sqrt(146)))=(sqrt(13)*sqrt7*sqrt(15))/(2*sqrt(73))` (точно также по формуле 5).

Сравнение площадей треугольников обычно опирается на одно из следующих утверждений:

$$ 2.<1>^<○>$$. Площади треугольников с одинаковой высотой относятся как длины соответствующих оснований. В частности, если точка `D` лежит на основании `AC` (рис. 6а), то

$$ 2.<2>^<○>$$. Площади треугольников с общим углом относятся как произведения сторон, заключающих этот угол (см. рис. 6б):

$$ 2.<3>^<○>$$. Площади подобных треугольников относятся как квадраты их

сходственных сторон, т. е. если `Delta ABC

DeltaA_1B_1C_1`, то `(S_(A_1B_1C_1))/(S_(ABC))=((A_1B_1)/(AB))^2`.

Все эти утверждения легко доказываются с использованием соответственно формул площади (1) и (2).

Обратим внимание на важное свойство медиан треугольника.

Три медианы треугольника разбивают его на `6` треугольников с общей вершиной и равными площадями.

Известно, что три медианы треугольника пересекаются в одной точке и делятся в отношении `2:1`, считая от вершины. Пусть `O` – точка пересечения медиан треугольника `DeltaABC` площади `S` (рис. 7а). Надо доказать, что площади всех шести треугольников с верш иной в точке `O`, составляющих треугольник `ABC`, равны между собой, т. е. равны `1/6S`.

Докажем, например, для треугольника `BOM`, что `S_(BOM)=1/6S_(ABC)`.

Точка `M` – середина стороны `BC` (рис. 7б), по утверждению $$ 2.<1>^<○>$$ о сравнении площадей `S_(ABM)=1/2S`. Медиана `BN`, пересекая медиану `AM` в точке `O` (рис. 7в), делит её в отношении `AO:OM=2:1`, т. е. `OM=1/3AM`. По тому же утверждению $$ 2.<1>^<○>$$ площадь треугольника `BOM` составляет `1//3` площади треугольника `ABM`, т. е.

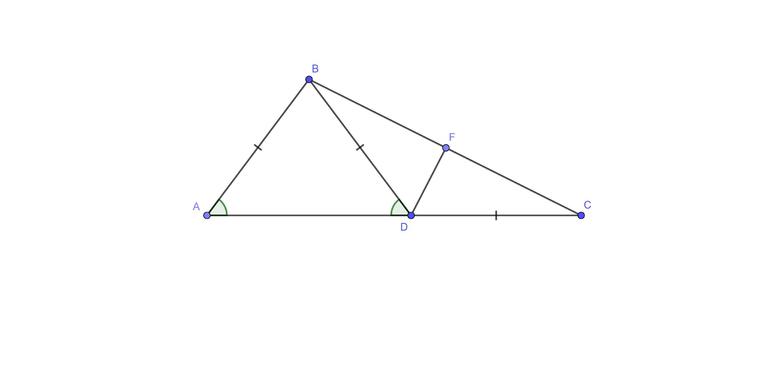
Дан треугольник `ABC`. Точка `D` лежит на стороне `AB`, `AD:DB=1:2`, точка `K` лежит на стороне `BC`, `BK:KC=3:2` (рис. 8а). Отрезки `AK` и `CD` пересекаются в точке `O`. Найти отношение площади четырёхугольника `DBKO` к площади треугольника `ABC`.

1. Обозначим `S_(ABC)=S`, `S_(DBKO)=sigma` и `S_(ADO)=a`. По утверждению $$ 2.<1>^<○>$$ имеем `S_(ABK)=a+sigma=3/5S` (так как `BK:BC=3:5`). Площадь `a` треугольника `ADO` найдём как часть площади треугольника `ADC`, зная, что `S_(ADC)=1/3S` (так как `AD:AB=1:3`).

2. Через точку `D` проведём прямую `DL“||“AK`. По теореме о пересечении сторон угла параллельными прямыми (`/_ABC`, `DL“||“AK`) имеем `(BL)/(LK)=(BD)/(AD)`, откуда `LK=y`.

По той же теореме (`/_DCB`, `OK“||“DL`) получим `(DO)/(DC)=(LK)/(LC)`, `DO=1/3DC`.

3. Теперь находим `S_(ADO):S_(ADC)=DO:DC`, `a=1/3(1/3S)=1/9S`.

(Можно по теореме Менелая для треугольника `BCD` и секущей `CD:`

`(BK)/(KC)*(CO)/(OD)*(DA)/(AB)=1 iff 3/2*(CO)/(OD)*1/3=1 iff CO=2OD=>OD=1/3DC`).

Находим площадь: `sigma=3/5S-a=(3/5-1/9)S=22/45S`.

Найти площадь треугольника, две стороны которого равны `3` и `7`, а медиана к третьей стороне равна `4` (рис. 9).

Пусть `AB=3`, `BC=7`, `AM=MC` и `BM=4`. Достроим треугольник `ABC` до параллелограмма, для этого на прямой `BM` отложим отрезок `MD=BM` и соединим точки: `A` с `D` и `C` с `D`. Противоположные стороны параллелограмма равны: `(DC=AB)` и равны площади треугольников `ABC` и `DBC` (общее основание `BC` и равные высоты из вершин `A` и `D`).

В треугольнике `DBC` известны все три стороны: `BC=7`, `DC=3`, `BD=2BM=8`.

Находим его площадь по формуле Герона: `p=9`, `S_(BCD)=6sqrt3`.

Значит и `S_(ABC)=6sqrt3`.

В решении этой задачи дополнительным построением получен треугольник, площадь которого равна площади заданного и легко вычисляется по данным задачи. Приведём ещё одну задачу, где сначала вычисляется площадь дополнительно построенной фигуры, а затем легко находится искомая площадь.

Найти площадь треугольника, если его медианы равны `3`, `4` и `5`.

Пусть `O` – точка пересечения медиан треугольника `ABC` (рис. 10) и пусть `m_a=AM=3`, `m_b=BN=4` и `m_c=CP=5`.

По свойству медиан `AO=2/3m_a`, `CO=2/3m_c` и `ON=1/3m_b`. В треугольнике `AOC` известны две стороны `AO` и `CO` и медиана третьей стороны `ON`. Площадь этого треугольника найдём как в предыдущей задаче.

Достроим треугольник `AOC` до параллелограмма `AOCD`, `S_(AOC)=S_(DOC)`, в треугольнике `DOC` известны три стороны:

`DO=2ON=2/3m_b`, `OC=2/3m_c`, `DC=AO=2/3m_a`.

Площадь треугольника `DOC` вычисляем по формуле Герона `S_1=S_(AOC)=S_(DOC)=8/3`. Сравним теперь площадь треугольника `ABC` (обозначим её `S`) с площадью треугольника `AOC`. Из теоремы 2 о медианах и площадях следует `S_(AOC)=S_(AON)+S_(NOC)=2*1/6S=1/3S`.

В следующей задаче докажем лемму об отношении площади треугольника к площади другого треугольника, построенного из медиан первого.

Найти отношение площади `S` треугольника к площади `S_0` треугольника, составленного из медиан первого.

Рассмотрим рис. 10. В построенном треугольнике `OCD` стороны таковы: `OC=2/3m_c`, `OD=2/3m_b`, `CD=2/3m_a`. Очевидно, что треугольник со сторонами `m_a`, `m_b`, `m_c` подобен (по третьему признаку) треугольнику со сторонами `2/3m_a`, `2/3m_b`, `2/3m_c`.

Из решения предыдущей задачи следует, что `S_(OCD)=S_1=1/3S` (здесь `S` – площадь треугольника `ABC`). Кроме того, площади подобных треугольников относятся как квадраты сходственных сторон, поэтому `(S_1)/(S_0)=(2/3)^2`. Таким образом, имеем `S_0=9/4S_1=3/4S`, т. е.

`S_(m_am_bm_c)=3/4S_(abc)`.

Из рассуждений в решении Примера 9 следует, что всегда существует треугольник со сторонами, равными медианам данного треугольника, поскольку всегда существует подобный ему треугольник со сторонами `2/3m_a`, `2/3m_b`, `2/3m_c`. Кроме того, становится ясным план построения треугольника по трём отрезкам, равным его медианам: сначала строится треугольник `OCD` (см. рис. 10) со сторонами `2/3m_a`, `2/3m_b`, `2/3m_c`, затем точка `N` – середина отрезка `OD`, потом точка `A` (из `AN=NC`) и точка `B` (из `OB=OD`). Это построение осуществимо, если существует треугольник `OCD`, т. е. если существует треугольник со сторонами `m_a`, `m_b`, `m_c`. Итак, вывод: три отрезка могут быть медианами некоторого треугольника тогда и только тогда, когда из них можно составить треугольник.

Около окружности радиуса `sqrt3` описан треугольник. Найти его площадь, если одна из его сторон точкой касания делится на отрезки `9` и `5`.

Пусть `AP=9`, `PC=5` (рис. 11) и пусть `BM=x`. По свойству касательных `AM=AP`, `CN=CP` и `BN=BM`, поэтому стороны треугольника таковы: `AC=14`, `AB=9+x`, `BC=5+x`, тогда `p=14+x`. (Заметим, что `p=AC+BM`!). По формулам площади (3) и (4) имеем: `S=pr=(14+x)sqrt3` и `S=sqrt((14+x)x*5*9)`. Приравниваем правые части, возводим в квадрат, приводим подобные члены, получаем `x=1`. Вычисляем площадь треугольника:

Приём, применённый в решении этой задачи, когда площадь фигуры выражается двумя различными способами, часто используется в задачах на доказательство.

Проведём два примера, в каждом выведем полезную формулу.

В треугольнике `ABC` угол `C` равен `varphi`, `AC=b`, `BC=a` (рис. 12). Доказать, что биссектриса `CD` равна `(2ab)/(a+b) cos varphi/2`.

Обозначим `CD=x`. Очевидно, что `S_(ABC)=S_(ACD)+S_(DCB)`. По формуле (2) `S_(ABC)=1/2 ab sin varphi`, `S_(ACD)=1/2 bx sin varphi/2`, `S_(BDC)=1/2 ax sin varphi/2`. Таким образом, имеем: `1/2 ab sin varphi=1/2(a+b)x sin varphi/2`. Используем формулу синуса двойного угла `sin varphi=2sin varphi/2 cos varphi/2`, получим:

`x=(2ab)/(a+b)cos varphi/2`.

называется окружность, касающаяся одной из сторон треугольника и продолжений двух других сторон. Таких окружностей, очевидно, три (рис. 13). Их радиусы обычно обозначаются `r_a`, `r_b`, `r_c` в зависимости от того, какой стороны окружность касается.

Вневписанная окружность касается стороны `a=BC` треугольника `ABC` (рис. 14). Доказать, что `S_(ABC)=r_a(p-a)`, где `2p=a+b+c`.

Центр окружности `I_a` лежит на пересечении биссектрисы угла `A` и биссектрис внешних углов при вершинах `B` и `C`. Легко видеть, что если `D`, `F` и `E` – точки касания, то `I_aD=I_aF=I_aE=r_a`.

Считаем площадь `S_0` четырёхугольника `ABI_aC`:

`S_0=S_(ABC)+S_(BCI_a)` и `S_0=S_(ABI_a)+S_(ACI_a)`, откуда

Площадь треугольника онлайн

С помощю этого онлайн калькулятора можно найти площадь треугольника. Для нахождения площади треугольника введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть смотрите ниже.

Площадь треугольника по основанию и высоте

Любой из сторон треугольника можно называть основанием треугольника. Если основание выбрана, то под словом “высота” понимают высоту треугольника, проведенную к основанию (Рис.1):

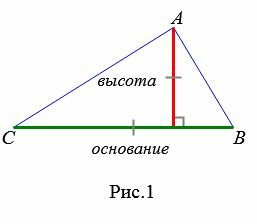
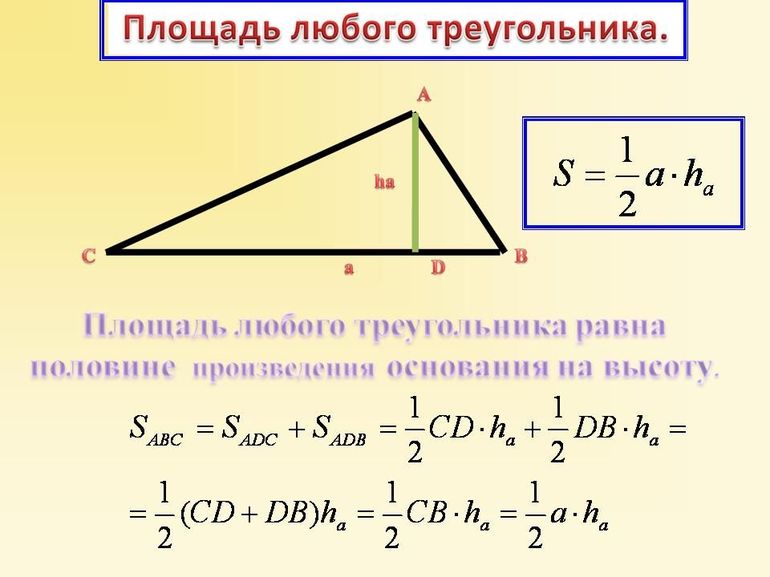
Теорема 1. Площадь треугольника равна половине произведения его основания на высоту.

Доказательство. Пусть AC основание треугольника ABC (Рис.2).

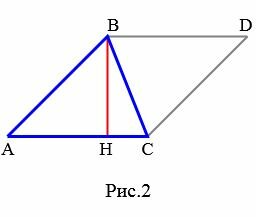
Проведем высоту BH. Обозначим через S площадь треугольника. Докажем, что

( small S= frac <large 1> <large 2>cdot AC cdot BH. )

Из вершины B проведем прямую, параллельную стороне AC, а из C − прямую, параллельную стороне AB. Поскольку ( small AC || BD ) и ( small AB || CD ), то ABDC является параллелограммой и, следовательно, ( small AC = BD ), ( small AB = CD . ) Тогда треугольники ABC и BCD равны по трем сторонам (см. статью на странице Треугольники. Признаки равенства треугольников). Так как площадь параллелограмма ABDC равна ( small S_=AC cdot BH, ) то площадь треугольника ABC (и BCD)равна половине площади параллелограмма:

Следствие 1. Если высоты треугольников равны, то их площади относятся как основания.

,

,

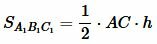Обозначим через k отношение

( small k= frac <large AC><large A_1C_1>. )

.

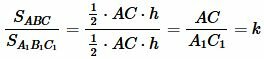То есть отношение площадей треугольников с равными высотами равно отношению их оснований.

Следствие 2. Площадь прямоугольного треугольника равна половине произведения его катетов.

Действительно. Поскольку в прямоугольном треугольнике катеты перпендикулярны друг другу, то один из них можно определить как основание, а другой − как высоту. Тогда по теореме 1, площадь прямоугольного треугольника равна половине произведения его катетов.

Площадь треугольника по двум сторонам и углу между ними

Теорема 2. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

Доказательство. Обозначим через S площадь треугольника ABC и пусть a=BC, b=AC (Рис.3). Докажем, что

.

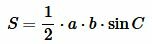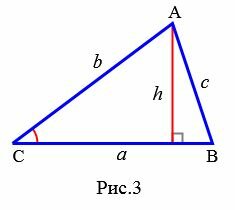
Площадь данного треугольника можно вычислить по формуле, полученной выше (теорема 1):

,

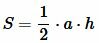(1)

где h − высота треугольника.

,

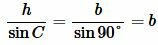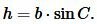(2)

Подставляя (2) в (1), получим:

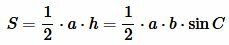
Площадь треугольника по стороне и прилежащим двум углам

Пусть известна сторона треугольника и две прилежащие углы (Рис.4).

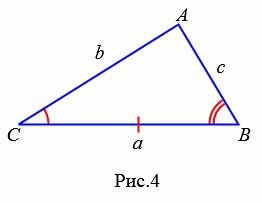
Найдем формулу площади этого треугольника. Обозначим через S площадь треугольника. Если у треугольника известны два угла, то можно найти и третий угол:

(4)

Найдем сторону b используя теорему синусов:

,

.

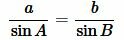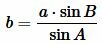(5)

В предыдующем параграфе мы вывели площадь треугольника по двум сторонам и углу между ними. Подставляя (4) и (5) в (3), получим:

.

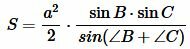(6)

Площадь треугольника по трем сторонам. Формула Герона

Для нахождения площади треугольника по трем сторонам используют формулу Герона:

,

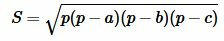(7)

где a, b, c − стороны треугольника, а p − полупериод треугольника:

.

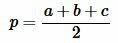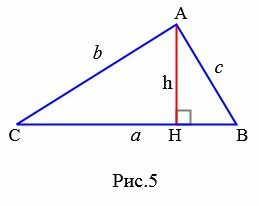
Доказательство формулы Герона. На рисунке 5 треугольник ABC имеет стороны a=BC, b=AC, c=AB. Проведем высоту h=AH. Обозначим x=CH. Тогда BH=a−x. Применим теорему Пифагора для треугольников AHC и AHB:

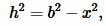(8)

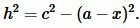(9)

Из (8) и (9) следует:

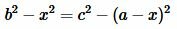
Откуда находим x:

,

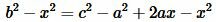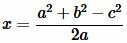(10)

Подставляя (10) в (8) найдем h:

Тогда площадь треугольника равна:

Преобразовав (12) получим формулу (7):

Площадь треугольника по трем сторонам и радусу описанной окружности

Пусть известны все три стороны треугольника и радиус описанной окружности (Рис.6). Докажем, что площадь треугольника равна: ( small S=frac<large abc><large 4R>. )

[spoiler title=”источники:”]

http://zftsh.online/articles/5257

http://matworld.ru/geometry/ploshchad-treugolnika.php

[/spoiler]

У этого термина существуют и другие значения, см. Теорема Пика.

Формула Пи́ка (или теорема Пи́ка) — классический результат комбинаторной геометрии и геометрии чисел,
даёт выражение для площади многоугольника с целочисленными вершинами.

Названа в честь Георга Пика, доказавшего её в 1899 году.

Формулировка[править | править код]

Площадь многоугольника с целочисленными вершинами^[1] равна
,
где В — количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника.

Следствия[править | править код]

• Площадь треугольника с вершинами в узлах и не содержащего узлов ни внутри, ни на сторонах (кроме вершин), равна 1/2.
  • Этот факт даёт геометрическое доказательство формулы для разности подходящих дробей цепной дроби.

Вариации и обобщения[править | править код]

• Многочлен Эрара даёт один из вариантов обобщения формулы Пика на старшие размерности.

где суммирование ведётся по всем целочисленным точкам и телесный угол при ; если лежит внутри , то считается что .^[2]

где обозначает площадь единичной сферы в .

Примечания[править | править код]

Литература[править | править код]

• В. В. Прасолов. Задачи по планиметрии. — М.: МЦНМО, 2001. — 584 с. — ISBN 5-900916-82-0.
• А. Кушниренко. Целые точки в многоугольниках и многогранниках // Квант. — 1977. — № 4. — С. 13—20.

Самый простой многоугольник и вектор

Чтобы найти площадь треугольника через векторы и известные координаты его вершин, необходимо подробнее познакомиться с этими геометрическими объектами. Знание их свойств позволяет легко вычислять разные характеристики изучаемой фигуры, включая периметр, высоту, углы при вершинах и другие. При этом используются универсальные математические операции, которые можно применять с успехом не только для треугольника, но и для других многоугольников.

Фигура на плоскости

Треугольник в геометрии представляет собой самый простой многоугольник, который лежит всегда в одной плоскости, даже если фигура рассматривается в трехмерном пространстве. Состоит он из сторон и вершины.

Сторон и вершин у фигуры по три. Сторона является отрезком, а вершина — это точка пересечения этих отрезков. Для нее характерен определенный угол. Все углы треугольника являются разными в общем случае, их сумма всегда соответствует 180°. Однако, существуют специальные типы фигуры, для которых либо два угла равны друг другу (равнобедренный), либо все три (равносторонний). В задачах называют треугольники по имени их трех вершин, обозначенных латинскими буквами, например, ABC или NPQ.

Для треугольника важное значение имеют следующие отрезки:

• делящий противоположную углу сторону пополам — медиана;
• разделяющий угол при вершине на два равных — биссектриса;
• падающий под прямым углом на противоположную углу сторону — высота.

Высота, например, используется для расчета площади фигуры. Для равностороннего треугольника все эти отрезки совпадают друг с другом для любой вершины, а для равнобедренного они одинаковы лишь для угла, образованного равными сторонами.

Направленный отрезок

Вектором называют линейный элемент, который имеет начало и конец. Для его определения удобнее всего использовать координатную плоскость. Она представляет собой две направленные оси, имеющие шкалу и пересекающиеся под углом 90°. Точка пересечения является началом координат и обозначается буквой O (0; 0). Здесь каждая из цифр указывает точку пересечение перпендикуляра, опущенного из рассматриваемого объекта к каждой из двух осей.

Если начало A (x0; y0) и конец B (x1; y1) вектора известны, тогда легко можно вычислить его собственные координаты. Делается это так:

AB- = B-A = (x1-x0; y1-y0).

Иными словами, чтобы получить вектор AB-, следует из соответствующих координат его конца вычесть его начало. Эта операция эквивалентна параллельному перемещению AB- в начало координатной плоскости, что говорит о существовании бесконечного количества одинаковых AB-векторов.

Направленные отрезки можно складывать, вычитать и умножать. Для каждой из операций существуют определенные правила. Если для сложения и вычитания речь идет о геометрических особенностях, то в случае умножения применяются исключительно алгебраические выражения. Вектор a- можно умножить на b- двумя принципиально разными способами:

1. Скалярно: (a-*b-). В этом случае мы получаем число. Правило умножения записывается следующим образом: (a-*b-) = |a-|*|b-|*cos (ab)=x1*x2+y1*y2. Здесь знаком модуля (||) обозначены длины соответствующих отрезков, cos (ab) — это косинус угла между a- и b-, при этом a-(x1; y1), b-(x2; y2). Этот тип произведения можно использовать для вычисления углов между направленными отрезками, а также для определения объема фигур в пространстве.
2. Векторно: [a-*b-]. Результатом этой операции является вектор, который перпендикулярен исходным, его направление (вверх или вниз) принято определять по правилу правой руки: четыре пальца должны быть направлены от конца a- к концу b-, тогда оттопыренный большой палец укажет направление их векторного произведения. Длина этого перпендикулярного вектора определяется так: [a-*b-] = |a-|*|b-|*sin (ab) = x1*y2-x2*y1. Векторное произведение используют для вычисления площадей фигур.

Методы вычисления площади по координатам

Задачи на вычисление площадей, периметров или объемов фигур по известным координатам их вершин являются типичными для школьного курса геометрии. В связи с развитием современных технологий школьники часто ищут в интернете, как решить треугольник онлайн по координатам. Тем не менее, существует ряд простых способов, которые позволяют быстро найти площадь фигуры, если известно расположение трех его вершин на координатной плоскости.

Универсальный подход

Этот метод можно применять всегда, независимо от того, какой тип треугольника рассматривается. Известно, что площадь фигуры вычисляется, как произведение половины стороны на опущенную на нее высоту: S = ½*a*h.

Пусть имеются координаты вершин заданного треугольника ABC:

• A (x1; y1);
• B (x2; y2);
• C (x3; y3).

Тогда координаты его векторов AB- и AC- выразятся так:

• AB- = (x2-x1; y2-y1);
• AC- = (x3-x1; y3-y1).

Если провести высоту h треугольника ABC к любой из этих сторон, например, к AC, то ее длина может быть рассчитана с использованием тригонометрической функции синуса:

h = AB*sin (α).

Здесь α является углом между векторами-сторонами AB- и AC-. Тогда формулу площади можно переписать в следующем виде: S = ½*a*h = ½*AC* AB*sin (α).

Можно заметить, что записанное выражение является не чем иным, как векторным произведением для AB- и AC-, поэтому можно переписать формулу для S так:

S = ½*[ AB-* AC- ] = ½*((x2-x1)*(y3-y1) — (y2-y1)*(x3-x1)).

Можно аналогично показать, что подобные выражения получаются для пар векторов AC-, BC- и AB-, BC-.

Рекомендуется не запоминать конечные выражения для площади треугольника, поскольку они являются несколько громоздкими, и при их использовании ученики могут запутаться. Для решения подобного рода задач достаточно понять свойства векторов и единственную универсальную формулу для S для любого типа треугольников.

Любопытно отметить, что векторное произведение при вычислении площади можно применять не только для треугольников, но и для любых четырехугольников. Так, в случае параллелограмма рассматриваемая характеристика будет точно равна векторному произведению любых смежных (непараллельных) его сторон.

Использование формулы Герона

Этот способ также может считаться универсальным, поскольку он применим к любым типам треугольников. В работе Герона Александрийского, которая называется «Метрика» и относится к I веку нашей эры, впервые было обнаружено выражение, позволяющее по длинам сторон рассматриваемой фигуры определить ее площадь. Формула имеет следующий вид:

S = (p*(p-a)*(p-b)*(p-c))^0,5.

Здесь p — полупериметр, a, b, c — длины сторон.

Последовательность этапов решения задачи можно выразить таким образом:

1. Необходимо определить координаты векторов, образующих стороны треугольника.
2. Затем, следует вычислить длины их сторон.
3. Посчитать полупериметр фигуры.
4. Применить формулу Герона.

Ключевым этапом является определение длины вектора. Пусть AB- имеет координаты (x1; y1), тогда его длина вычисляется так:

|AB-| = (x1 ² + y1 ² )^0,5.

Длина любого вектора как на плоскости, так и в пространстве, вычисляется, как сумма квадратов всех его координат, взятых под корень.

Очевидно, что можно записать общее выражение для площади треугольника через координаты с использованием формулы Герона, но оно будет слишком громоздким, поэтому нет никакого смысла запоминать его.

Другие способы

Существуют эмпирические правила, которые можно запомнить и легко решать задачи на определение площади треугольника. Пусть координаты его вершин задаются так: A (x1; y1), B (x2; y2), C (x3; y3). Предположим, что порядок вершин A, B, C расположен против часовой стрелки, тогда существуют следующие правила определения площади ABC:

1. Можно воспользоваться формулой: S = ½*(x1*(y2-y3) + x2*(y3-y1) + x3*(y1-y2)). То есть выбирается первая координата вершины и умножается на разность вторых координат двух других вершин, возникающих против хода стрелки часов от первой. Затем, все три члена складываются и делятся на 2.
2. Матричный способ. Необходимо выписать в столбик пары координат каждой вершины против часовой стрелки и завершить координатами исходной. После этого следует сложить три попарных произведения первой и второй координат двух соседних вершин, а затем, вычесть три попарных произведений второй и первой координат тех же вершин. Результат поделить пополам. Например: (x1; y1) (x2; y2) (x3; y3) (x1; y1). S = ½*(x1*y2 + x2*y3 + x3*y1 — y1*x2 — y2*x3 — y3*x1).

Решение задачи

Дана фигура АВС. Найдите площадь треугольника, вершины которого имеют координаты A (1; -3), B (2; 5), C (-2; -2).

Для нахождения решения следует обратиться за помощью к универсальному способу. Сначала необходимо выбрать два вектора, образующих стороны треугольника. Пусть это будут AB- и BC-. Теперь нужно знать их координаты. Они равны:

• AB- = (2−1; 5-(-3)) = (1; 8);
• BC- = (-2−2; -2−5) = (-4; -7).

Чтобы рассчитать площадь, достаточно вычислить полупроизведение векторное для выбранных направленных отрезков: S = ½*[AB-*BC-] = ½*(1*(-7)-8*(-4)) = 12,5 квадратных единиц.

Таким образом, существует несколько методик вычисления площади треугольника, если известны координаты его вершин. Все они сводятся к использованию свойств векторов и известных формул. Существуют также выражения, которые следует запомнить, чтобы решать подобные задачи.

Площадь фигуры (треугольник, четырёхугольник, трапеция и др.) по клеточкам (клеткам). Какие есть формулы? Есть способ, при котором надо воспользоваться формулой, основой которой будет понятие узла, узла внутреннего и узла внешнего. Узел это пересечение линий, образующих эти самые клеточки. Внешние узлы, это узлы, находящиеся на сторонах и вершинах геометрических фигур, площади которых нам надо найти. А внутренние узлы, это узлы внутри этих фигур. Клеточки у нас со сторонами равными одному сантиметру (1 см). Формула, о которой идет речь, называется формула Пика. Выглядит она вот так: И по ней очень просто посчитать площадь фигуры S. В этой формуле M это количество внешних узлов, N – количество внутренних узлов. Приведем пример, возьмем геометрическую фигуру параллелограмм: Внутренние узлы – синие – N – их у нас 20. Внешние узлы – красные – М – их у нас 18 и их количество нам надо поделить на два, получится 18/2 = 9 узлов. Складываем 9 + 20 и вычитаем единицу: 20 + 9 – 1 = 28 см². Еще один пример: S = 14/2 + 43 – 1 = 49 см². система выбрала этот ответ лучшим Ксарф­акс [156K] 6 лет назад  Допустим, у нас есть произвольная фигура, построенная на листе в клетку. Необходимо вычислить её площадь. Площадь фигуры по клеточкам Для того, чтобы найти площадь любой фигуры по клеточкам, можно использовать формулу Пика. Данная формула основана на подсчёте количества узлов, лежащих внутри фигуры и на её границе. Узел – это точка, которая лежит на пересечении 2 линий данной сетки: вертикальных и горизонтальных. Площадь фигуры по клеточкам находится по формуле: N – количество узлов, которые находятся внутри фигуры. M – количество узлов, которые находятся на границах (на вершинах и сторонах). Примеры нахождения площади по клеточкам 1) Найдём площадь треугольника. Будем считать, что одна клетка – это 1 см. Отметим внутренние узлы и узлы, которые находятся на границах. N = 7 (внутренние). M = 8 (узлы на границах). Площадь треугольника S = 7 + 8/2 – 1 = 10 см². 2) Найдём площадь трапеции по клеточкам, одна клетка – это 1 см. Отметим все узлы и подсчитаем их количество. N = 11 (внутренние). M = 12 (узлы на границах). Площадь трапеции S = 11 + 12/2 – 1 = 16 см². 3) Найдём площадь произвольного многоугольника. Одна клетка – это 1 см. Отметим внутренние узлы и узлы, расположенные на границах фигуры. Подсчитаем их количество. N = 6 (внутренние узлы). M = 8 (узлы на границах). Площадь многоугольника S = 6 + 10/2 – 1 = 10 см². Марин­а Волог­да [294K] 3 года назад  Такие задачи очень часто встречаются, когда известен размер клеточки и дана фигура. Вот пример таких задач: Решение зависит от того, какая фигура дана и как именно она размещена относительно клеточек. Возьмем простой пример, необходимо вычислить площадь вот такого треугольника: Вспоминаем правило: Теперь считаем, сколько клеточек треугольник в длину и сколько в высоту. У нас получается 2 в высоту и 6 в длину. Подставляем к формуле: S = 1/2 х 2 х 6 = 6 см2. Считаем по клеточкам, подставляя формулу Пика: Целых клеточек у нас 3. Теперь считаем, сколько не целых: 6. Делим их на 2. S = 3 + 6:2 = 6 см2. А теперь высчитываем по формуле Пика: количество узлов сетки внутри – 2, количество узлов сетки, лежащих на границах – 10. Подставляем к формуле и получаем – 2 + 10:2 – 1 = 6 см2. Теперь давайте рассмотрим вот такой треугольник: Чтобы найти площадь, вспоминаем правило: Считаем клеточки и подставляем в формулу: S = 1/2 х 2 х 6 = 6 см2. А теперь находим по клеточкам: целых клеточек 2, не целых клеточек 8. Подставляем в формулу: 2 + 8:2 = 6 см2. Пробуем сделать по формуле Пика: количество узлов сетки внутри – 3, количество узлов сетки, лежащих на границах – 8. Подставляем к формуле и получаем – 3 + 8:2 – 1 = 6 см2. Enot-Nina [110K] 3 года назад  Найти площадь геометрической фигуры можно самыми разными способами: Самый простой вариант – это вручную посчитать клеточки – целые и половинки также поскладывать. Простой, хотя и не самый быстрый и может не самый точный способ, но он работает. Чтобы легче было считать, достаточно расчертить фигуру на более простые. Есть еще один способ – это использовать давно разработанную формулу. Это так называемая формула Пика. Для нее нужно посчитать количество узлов – точек пересечения клеточек, что окружены фигурой (находятся внутри нее), а также подсчитать количество пограничных узлов – по контуру фигуры. Вот на картинке наглядно показано, как ее можно применять, чтоб посчитать площадь любой фигуры по клеточкам: Барха­тные лапки [382K] 3 года назад  Площадь любого многоугольника можно посчитать по клеточкам. Для этого применяем формулу Пика. На нашем рисунке В – количество узловых клеточек внутри фигуры, Г – количество узлов на границе . Узлы – пересечение двух линий. многоугольника. Площадь равна S = В + Г/2 – 1 Считаем точки на рисунке и подставляем в формулу. – 10 + 7/2 -1 = 12,5. Таким образом можно посчитать площадь, если вершины фигуры лежат в узлах. Ann Luka [2.8K] 6 лет назад  Чтобы найти площадь фигуры по клеточкам, нужно посчитать сколько в фигуре целых клеточек. Потом нужно посчитать сколько не целых и поделить их количество на 2. Добавить к получившемуся числу количество целых клеточек – это и будет правильный ответ. Например. В треугольнике 3 целых клетки и 4 не целых. 3+4/2=5 пощадь треугольника 5 клеток. Outli­ne [18.3K] 3 года назад  Для того, чтобы определить площадь фигуры на бумаге в клеточку есть универсальная формула Пика, позволяющая вычислить площадь изображения, но в только в том случае, если вершины искомой фигуры имеют целые (натуральные числа) координаты. Называется эта формула, в честь Георга Пика: S=В + Г / 2 − 1 В этой формуле буквенные обозначения означают следующее: В — количество целочисленных точек внутри многоугольника; Г — количество целочисленных точек на границе (вершинах и сторонах) многоугольника; S – площадь фигуры. Здесь используется понятие “целочисленные” – это те, точки, которые расположены на пересечениях сетки (в ее узлах). Для примера, найдем площадь треугольника: Обозначим внутренние точки нашей фигуры красными кружками, а те, что на границах – синим цветом. Считаем красные и синие точки: В=12, Г=4. Исходя из подсчетов определяем площадь треугольника по формуле: S=В+Г/2-1=12+2-1=13. Можно убедиться в правильность проведенных выше расчетах. Рассчитываем площадь квадрата, обведенного красным, и вычитаем площади зеленого, синего и фиолетового треугольников: S квадрата равна 36, площади треугольников: синего – 6, зеленого – 2, фиолетового – 15. Исходя из полученных данных, S белого треугольника равна 13: S=36-6-15-2=13. Kriti­kSPb [93.6K] 3 года назад  Подсчет клеточек – дело полезное. С их помощью можно найти площадь геометрической фигуры. Достаточно воспользоваться формулой, доказанной Георгом Пиком в 1899 году. Подходит для расчета площади фигур с прямыми сторонами и целым количеством углов, чаще всего применяют для нахождения площади разносторонних треугольников и многоугольников с числом углов больше 4-х. На теорему Пика есть задания в ЕГЭ. 12777­1 [272K] 3 года назад  Сначала я подумал, что нужно будет фигуру, которая указана на рисунке в клеточку разбить по фигурам так, чтобы можно посчитать площадь каждой фигуры по-отдельности, но оказалось все намного проще. Существует для данной задачи специальная формула Пика, которая выглядит следующим образом: Площадь = В + Г/2 – 1, где: В – количество целочисленных точек внутри многоугольника. Г – количество целочисленных точек на границе многоугольника. Теперь разберемся на примере, у нас есть такой пример: Перед нами трапеция. Допустим площадь одной клетки 1 кв.см. Теперь можно воспользоваться формулой: 11+12/2-1=16 кв.см. Бекки Шарп [71.2K] 3 года назад  Найти площадь фигуры можно если вершины фигуры находятся в уголках клеточек, так называемые Целочисленные вершины или узловые точки. Решать задачу будем по формуле Пика, где В – количество внутренних узловых точек, Г – количество граничных узловых точек, Вот такая фигура у нас – Считаем точки и подставляем в формулу: S = 17 + 14/2 – 1 = 23 Ответ мы получаем в квадратных единицах, то есть клеточках. Знаете ответ?