Как найти площадь треугольника по заданным вершинам

Как найти площадь треугольника по координатам его вершин?

1способ:

Найти длины трёх сторон треугольника и вычислить площадь по формуле Герона. Способ удобен, если длины сторон являются целыми числами. В противном случае предстоят громоздкие вычисления.

2 способ:

вывести формулу для нахождения площади и использовать её для вычисления.

Утверждение

Площадь треугольника ABC с вершинами в точках A(x₁;y₁), B(x₂;y₂), C(x₃;y₃) можно вычислить с помощью формулы

   

Доказательство:

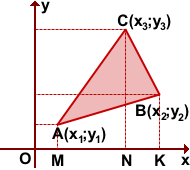Рассмотрим треугольник ABC,

A(x₁;y₁), B(x₂;y₂), C(x₃;y₃)

Опустим перпендикуляры из вершин треугольника на координатные оси.

   

   

   

   

   

   

   

   

   

   

   

   

   

С учетом вариантов взаимного расположения точек A, B и C формула для вычисления площади треугольника по координатам его вершин приобретает вид:

   

Что и требовалось доказать.

3 способ:

Найти длины двух сторон и косинус угла между ними и вычислить площадь треугольника через стороны и синус угла между ними.

4 способ:

Найти длину и уравнение одной стороны треугольника и длину высоты, проведённой к этой стороне. Вычислить площадь через сторону и высоту.

Рассмотрим эти способы на конкретном примере.

Найти площадь треугольника, вершины которого имеют координаты A(-1;-3), B(3;4), C(5;-5).

1 способ:

Находим длины сторон треугольника ABC.

   

   

   

   

   

   

Поскольку длины сторон выражены иррациональными числами, вычислять площадь треугольника по формуле Герона — не самый лучший способ.

2 способ:

Подставляем в формулу x₁=-1, y₁=-3, x₂=3, y₂=4, x₃=5, y₃=-5:

   

   

3 способ:

Угол A образован векторами AC и AB. Отсюда

   

Находим координаты векторов:

   

   

   

   

   

   

Скалярное произведение

   

Длины AB и AC уже знаем:

   

   

   

Синус и косинус одного угла связаны соотношением:

   

Синус угла от 0° до 180° является положительным числом, поэтому

   

   

Отсюда

   

   

4 способ:

Найдём уравнение прямой AB. Подставляем координаты A и B в уравнение y=kx+b:

   

Отсюда k=7/4, b=-5/4

   

   

Найдём расстояние от точки C до прямой AB:

   

Это расстояние равно высоте треугольника, проведённой из вершины C к стороне AB. Отсюда

   

Самый простой многоугольник и вектор

Чтобы найти площадь треугольника через векторы и известные координаты его вершин, необходимо подробнее познакомиться с этими геометрическими объектами. Знание их свойств позволяет легко вычислять разные характеристики изучаемой фигуры, включая периметр, высоту, углы при вершинах и другие. При этом используются универсальные математические операции, которые можно применять с успехом не только для треугольника, но и для других многоугольников.

Фигура на плоскости

Треугольник в геометрии представляет собой самый простой многоугольник, который лежит всегда в одной плоскости, даже если фигура рассматривается в трехмерном пространстве. Состоит он из сторон и вершины.

Сторон и вершин у фигуры по три. Сторона является отрезком, а вершина — это точка пересечения этих отрезков. Для нее характерен определенный угол. Все углы треугольника являются разными в общем случае, их сумма всегда соответствует 180°. Однако, существуют специальные типы фигуры, для которых либо два угла равны друг другу (равнобедренный), либо все три (равносторонний). В задачах называют треугольники по имени их трех вершин, обозначенных латинскими буквами, например, ABC или NPQ.

Для треугольника важное значение имеют следующие отрезки:

• делящий противоположную углу сторону пополам — медиана;
• разделяющий угол при вершине на два равных — биссектриса;
• падающий под прямым углом на противоположную углу сторону — высота.

Высота, например, используется для расчета площади фигуры. Для равностороннего треугольника все эти отрезки совпадают друг с другом для любой вершины, а для равнобедренного они одинаковы лишь для угла, образованного равными сторонами.

Направленный отрезок

Вектором называют линейный элемент, который имеет начало и конец. Для его определения удобнее всего использовать координатную плоскость. Она представляет собой две направленные оси, имеющие шкалу и пересекающиеся под углом 90°. Точка пересечения является началом координат и обозначается буквой O (0; 0). Здесь каждая из цифр указывает точку пересечение перпендикуляра, опущенного из рассматриваемого объекта к каждой из двух осей.

Если начало A (x0; y0) и конец B (x1; y1) вектора известны, тогда легко можно вычислить его собственные координаты. Делается это так:

AB- = B-A = (x1-x0; y1-y0).

Иными словами, чтобы получить вектор AB-, следует из соответствующих координат его конца вычесть его начало. Эта операция эквивалентна параллельному перемещению AB- в начало координатной плоскости, что говорит о существовании бесконечного количества одинаковых AB-векторов.

Направленные отрезки можно складывать, вычитать и умножать. Для каждой из операций существуют определенные правила. Если для сложения и вычитания речь идет о геометрических особенностях, то в случае умножения применяются исключительно алгебраические выражения. Вектор a- можно умножить на b- двумя принципиально разными способами:

1. Скалярно: (a-*b-). В этом случае мы получаем число. Правило умножения записывается следующим образом: (a-*b-) = |a-|*|b-|*cos (ab)=x1*x2+y1*y2. Здесь знаком модуля (||) обозначены длины соответствующих отрезков, cos (ab) — это косинус угла между a- и b-, при этом a-(x1; y1), b-(x2; y2). Этот тип произведения можно использовать для вычисления углов между направленными отрезками, а также для определения объема фигур в пространстве.
2. Векторно: [a-*b-]. Результатом этой операции является вектор, который перпендикулярен исходным, его направление (вверх или вниз) принято определять по правилу правой руки: четыре пальца должны быть направлены от конца a- к концу b-, тогда оттопыренный большой палец укажет направление их векторного произведения. Длина этого перпендикулярного вектора определяется так: [a-*b-] = |a-|*|b-|*sin (ab) = x1*y2-x2*y1. Векторное произведение используют для вычисления площадей фигур.

Методы вычисления площади по координатам

Задачи на вычисление площадей, периметров или объемов фигур по известным координатам их вершин являются типичными для школьного курса геометрии. В связи с развитием современных технологий школьники часто ищут в интернете, как решить треугольник онлайн по координатам. Тем не менее, существует ряд простых способов, которые позволяют быстро найти площадь фигуры, если известно расположение трех его вершин на координатной плоскости.

Универсальный подход

Этот метод можно применять всегда, независимо от того, какой тип треугольника рассматривается. Известно, что площадь фигуры вычисляется, как произведение половины стороны на опущенную на нее высоту: S = ½*a*h.

Пусть имеются координаты вершин заданного треугольника ABC:

• A (x1; y1);
• B (x2; y2);
• C (x3; y3).

Тогда координаты его векторов AB- и AC- выразятся так:

• AB- = (x2-x1; y2-y1);
• AC- = (x3-x1; y3-y1).

Если провести высоту h треугольника ABC к любой из этих сторон, например, к AC, то ее длина может быть рассчитана с использованием тригонометрической функции синуса:

h = AB*sin (α).

Здесь α является углом между векторами-сторонами AB- и AC-. Тогда формулу площади можно переписать в следующем виде: S = ½*a*h = ½*AC* AB*sin (α).

Можно заметить, что записанное выражение является не чем иным, как векторным произведением для AB- и AC-, поэтому можно переписать формулу для S так:

S = ½*[ AB-* AC- ] = ½*((x2-x1)*(y3-y1) — (y2-y1)*(x3-x1)).

Можно аналогично показать, что подобные выражения получаются для пар векторов AC-, BC- и AB-, BC-.

Рекомендуется не запоминать конечные выражения для площади треугольника, поскольку они являются несколько громоздкими, и при их использовании ученики могут запутаться. Для решения подобного рода задач достаточно понять свойства векторов и единственную универсальную формулу для S для любого типа треугольников.

Любопытно отметить, что векторное произведение при вычислении площади можно применять не только для треугольников, но и для любых четырехугольников. Так, в случае параллелограмма рассматриваемая характеристика будет точно равна векторному произведению любых смежных (непараллельных) его сторон.

Использование формулы Герона

Этот способ также может считаться универсальным, поскольку он применим к любым типам треугольников. В работе Герона Александрийского, которая называется «Метрика» и относится к I веку нашей эры, впервые было обнаружено выражение, позволяющее по длинам сторон рассматриваемой фигуры определить ее площадь. Формула имеет следующий вид:

S = (p*(p-a)*(p-b)*(p-c))^0,5.

Здесь p — полупериметр, a, b, c — длины сторон.

Последовательность этапов решения задачи можно выразить таким образом:

1. Необходимо определить координаты векторов, образующих стороны треугольника.
2. Затем, следует вычислить длины их сторон.
3. Посчитать полупериметр фигуры.
4. Применить формулу Герона.

Ключевым этапом является определение длины вектора. Пусть AB- имеет координаты (x1; y1), тогда его длина вычисляется так:

|AB-| = (x1 ² + y1 ² )^0,5.

Длина любого вектора как на плоскости, так и в пространстве, вычисляется, как сумма квадратов всех его координат, взятых под корень.

Очевидно, что можно записать общее выражение для площади треугольника через координаты с использованием формулы Герона, но оно будет слишком громоздким, поэтому нет никакого смысла запоминать его.

Другие способы

Существуют эмпирические правила, которые можно запомнить и легко решать задачи на определение площади треугольника. Пусть координаты его вершин задаются так: A (x1; y1), B (x2; y2), C (x3; y3). Предположим, что порядок вершин A, B, C расположен против часовой стрелки, тогда существуют следующие правила определения площади ABC:

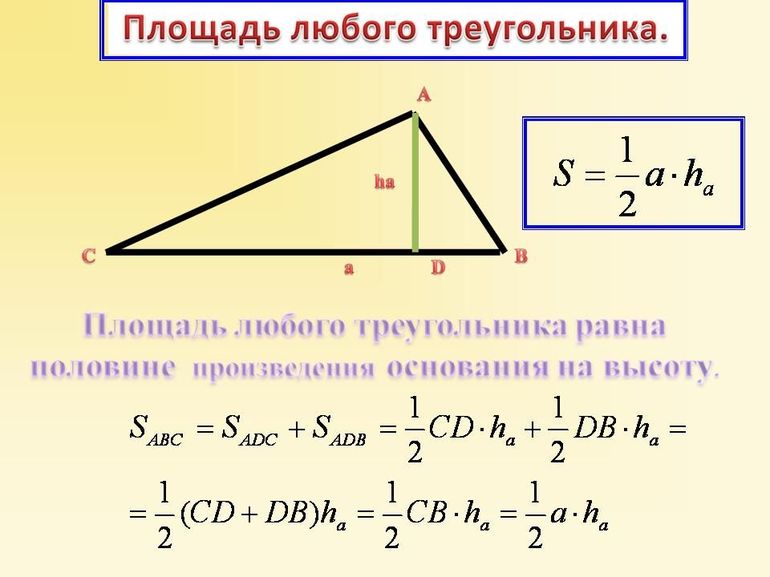
1. Можно воспользоваться формулой: S = ½*(x1*(y2-y3) + x2*(y3-y1) + x3*(y1-y2)). То есть выбирается первая координата вершины и умножается на разность вторых координат двух других вершин, возникающих против хода стрелки часов от первой. Затем, все три члена складываются и делятся на 2.
2. Матричный способ. Необходимо выписать в столбик пары координат каждой вершины против часовой стрелки и завершить координатами исходной. После этого следует сложить три попарных произведения первой и второй координат двух соседних вершин, а затем, вычесть три попарных произведений второй и первой координат тех же вершин. Результат поделить пополам. Например: (x1; y1) (x2; y2) (x3; y3) (x1; y1). S = ½*(x1*y2 + x2*y3 + x3*y1 — y1*x2 — y2*x3 — y3*x1).

Решение задачи

Дана фигура АВС. Найдите площадь треугольника, вершины которого имеют координаты A (1; -3), B (2; 5), C (-2; -2).

Для нахождения решения следует обратиться за помощью к универсальному способу. Сначала необходимо выбрать два вектора, образующих стороны треугольника. Пусть это будут AB- и BC-. Теперь нужно знать их координаты. Они равны:

• AB- = (2−1; 5-(-3)) = (1; 8);
• BC- = (-2−2; -2−5) = (-4; -7).

Чтобы рассчитать площадь, достаточно вычислить полупроизведение векторное для выбранных направленных отрезков: S = ½*[AB-*BC-] = ½*(1*(-7)-8*(-4)) = 12,5 квадратных единиц.

Таким образом, существует несколько методик вычисления площади треугольника, если известны координаты его вершин. Все они сводятся к использованию свойств векторов и известных формул. Существуют также выражения, которые следует запомнить, чтобы решать подобные задачи.

• 

Найти площадь треугольника по координатам его вершин

Точки треугольника дают однозначное понятие его расположения в пространстве, зная их положение можно найти площадь треугольника по координатам его вершин.

Выполнить процедуру по нахождению площади исходя из координат вершин можно несколькими путями.

Формула Герона

В этой формуле используются размеры сторон фигуры. Поэтому нахождение площади следует начать с вычисления размеров сторон. Обозначим вершины как A₁ (X_₁,Y_₁,Z_₁), B₂ (X_₂,Y_₂,Z_₂) и C₃ (X_₃,Y_₃,Z_₃). Тогда размеры сторон треугольника можно рассчитать как:

Чтобы упростить расчеты можно ввести понятие полупериметра (Р).

Находим площадь по формуле Герона используя полупериметр. В общем виде она выглядит так:

Интерактивные онлайн калькуляторы

Найти площадь треугольника по координатам вершин можно и непосредственно в онлайн. Скрипты подобного рода проделают всю работу за вас. Все что необходимо ввести – это координаты вершин треугольника. Единственным недостатком калькуляторов является отсутствие разъяснений расчетов по каждому шагу.
Воспользоваться таким калькулятором можно на сайте planetcalc.ru.

Онлайн калькулятор расчета площади треугольника по координатам его вершин

Примечание: дробные числа записывайте
через точку, а не запятую.

Округлять до -го знака после запятой.

Прямоугольная система координат на плоскости и ее применение с примерами

Содержание:

Прямоугольная система координат на плоскости и ее применение к простейшим задачам

Прямоугольные координаты точки на плоскости

Координатами точки на плоскости называются числа, определяющие положение этой точки на плоскости.

Прямоугольные декартовы координаты (по имени математика Декарта) на плоскости вводятся следующим образом: на этой плоскости выбираются точка О (начало координат) и проходящие через нее взаимно перпендикулярные направленные прямые Ох и Оу (оси координат) (рис. 1). Для удобства рассмотрения будем предполагать, что ось Ох 0ось абсцисс) горизонтальна и направлена слева направо, а ось Оу (ось ординат) вертикальна и направлена снизу вверх; таким образом, ось О у повернута относительно оси Ох на угол 90° против хода часовой стрелки 1 ). Кроме того, выбирается единица масштаба для измерения расстояний.

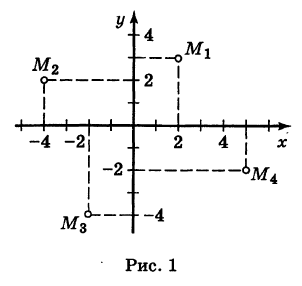
Для данной точки М введем в рассмотрение два числа: абсциссу х и ординату у этой точки.

Абсциссой х называется число, выражающее в некотором масштабе расстояние от точки до оси ординат, взятое со знаком плюс, если точка лежит вправо от оси ординат, и со знаком минус, если точка лежит влево от оси ординат. Ординатой у называется число, выражающее в некотором масштабе (обыкновенно в том же, как и для абсциссы) расстояние от точки до оси абсцисс, взятое со знаком плюс, если точка лежит выше оси абсцисс, и со знаком минус, если точка лежит ниже оси абсцисс.

Эти два числа х и у и принимаются за координаты точки М, так как они полностью определяют положение точки на плоскости, а именно: каждой паре чисел х и у соответствует единственная точка, координатами которой являются эти числа; и обратно, каждая точка плоскости имеет определенные координаты х и у. Если точка М имеет координаты х и у, то это обстоятельство обозначают так: М (х, у) (на первом месте ставится абсцисса х, а на втором — ордината у). При записи координат знак плюс, как обычно, можно опускать.

Оси Ох и Оу разбивают плоскость на четыре части, называемые квадрантами. Производя нумерацию квадрантов (I, II, III и IV) в направлении против хода часовой стрелки, отправляясь от того квадранта, где обе координаты положительны, получим следующую таблицу знаков координат: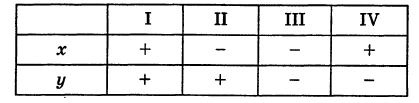

Отрезок ОМ у соединяющий начало координат О с точкой М (рис. 2), называется ее радиусом-вектором. Обозначая через ф угол, образованный отрезком ОМ с положительным направлением оси Ох, и через 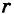его длину, для точки М, лежащей в I квадранте, из треугольников ОММ’ и ОММ” получим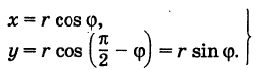

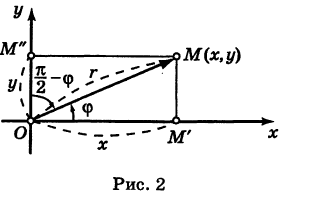
Нетрудно убедиться, что формулы (1) будут справедливы для координат точек всех квадрантов. Таким образом, знак абсциссы х точки М совпадает со знаком косинуса, а знак ее ординаты у — со знаком синуса в соответствующем квадранте.

Легко видеть, что если точка лежит на оси абсцисс, то ее ордината у равна нулю; если же она лежит на оси ординат, ее абсцисса х равна нулю, и обратно. Следовательно, если точка совпадает с началом координат, то равны нулю обе ее координаты.

В дальнейшем прямоугольные декартовы координаты для краткости будем называть просто прямоугольными координатами.

В следующих параграфах рассмотрим некоторые простейшие задачи на применение прямоугольных координат на плоскости.

Преобразование прямоугольной системы координат

При решении задач иногда выгодно вместо данной прямоугольной системы координат 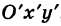выбрать другую прямоугольную систему координат О’х’у определенным образом ориентированную относительно первой. Например, при межпланетных путешествиях можно пользоваться системой координат, связанной с центром Земли (геоцентрическая система координат); однако более удобно использовать систему координат, связанную с центром Солнца (гелиоцентрическая система координат).

Возникает вопрос о том, как от одной системы координат перейти к другой.

Рассмотрим сначала простейший случай (рис. 3), когда оси «новой системы координат» О’х’у’ параллельны соответствующим осям «старой системы координат о Оху и имеют одинаковые направления с ними (параллельный перенос системы координат).

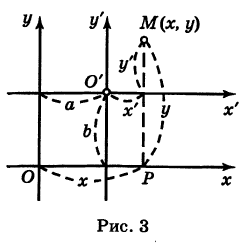
Пусть начало новой системы координат — точка О’ — имеет координаты (а, Ь) в старой системе координат. Точка М плоскости со «старыми координатами» (х, у) будет иметь некоторые «новые координаты» [х у’] (для ясности мы их обозначаем квадратными скобками). Из рис. 3 непосредственно получаем

х’ = х – а, у’ = у – b, (1)

т. е. новые координаты точки равны ее старым координатам минус старые координаты нового начала.

Обратно, из (1) находим

х = х’ + а, у = у’ + Ь. (2)

Пусть теперь «новая система» координат Ох’у при неизменном начале О, повернута относительно «старой системы» Оху на угол а (рис. 4), т. е. 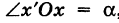, причем а считается положительным, если поворот осуществляется против хода часовой стрелки, и отрицательным — в противоположном случае (поворот системы координат).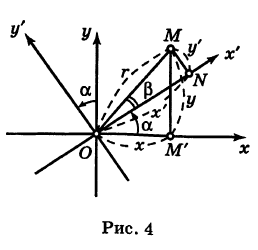

Обозначим через 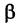угол, образованный радиусом-вектором г = ОМ точки М с осью Ох’; тогда отрезок ОМ, с учетом знака угла 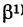), будет составлять с осью Ох угол 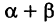. Отсюда на основании формул (1) из при любом расположении точки М имеем

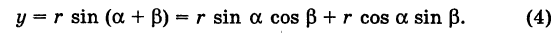
Так как новые координаты точки М, очевидно, есть

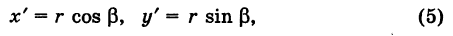
то из формул (3) и (4) получаем

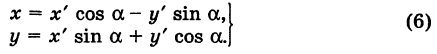
Для запоминания формул (6) используют следующий мнемонический прием: говорят, что первая формула (6) содержит полный беспорядок, а вторая — полный порядок. Действительно, в первой формуле на первом месте стоит cos, на втором — sin; кроме того, присутствует знак минус. Во второй формуле (6) никаких нарушений правильности в этом смысле нет.

Формулы (6) выражают старые координаты х и у точки М через ее новые х’ и у’. Чтобы выразить новые координаты х’ и у’ через старые х и у, достаточно разрешить систему (6) относительно х’и у’. Однако можно поступить проще, а именно принять систему Ох’у’ за «старую», а систему Оху за «новую». Тогда, учитывая, что вторая система повернута относительно первой на угол — а, заменяя в формулах (6) х’ и у’ соответственно на х и у и обратно и принимая во внимание, что cos (-a) = cos a, sin (-a) = -sin a, будем иметь

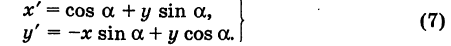
Наконец, в общем случае, когда новое начало координат есть точка О’ (a, Ь) и ось О’х’ образует с осью Ох угол а, соединяя формулы (2) и (6), находим

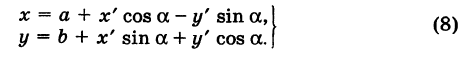
Здесь угол Р считается положительным, если радиус-вектор ОМ повернут относительно оси Ох’ против хода часовой стрелки, и отрицательным, если он повернут относительно этой оси по ходу часовой стрелки.

Аналогично, из формул (1) и (7) получаем

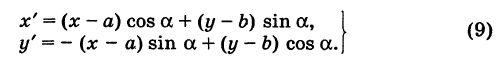
Из формул (8) и (9) вытекает, что формулы перехода от одной прямоугольной системы координат к другой прямоугольной системе координат являются линейными функциями как новых, так и старых координат, т. е. содержат эти координаты в первой степени.

Пример:

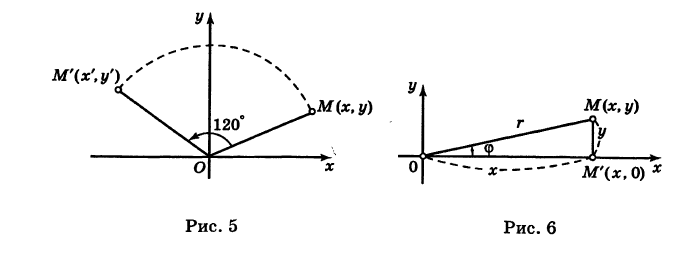
Отрезок ОМ, где точка М имеет координаты (х, г/), повернут на угол а = 120° против хода часовой стрелки (рис. 5). Каковы будут координаты х’ и у’ нового положения М’ точки М?

Решение:

Предполагая, что с точкой М связана подвижная система координат Ох’у на основании формул (6) будем иметь

Расстояние между двумя точками на плоскости

1) Найдем сначала расстояние г от начала координат О (0, 0) до точки М (х, у) (рис. 6).

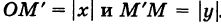Расстояние г = ОМ, очевидно, является гипотенузой прямоугольного ОММ’ с катетами . По теореме Пифагора получаем

Таким образом, расстояние от начала координат до некоторой точки равно корню квадратному из суммы квадратов координат этой точки.

2) В общем случае, пусть для точек A 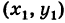и Б 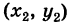(рис. 7) требуется найти расстояние d = АВ между этими точками.

Выберем новую систему координат Ах’у’ начало которой совпадает с точкой А и оси которой параллельны прежним осям и имеют, соответственно, одинаковые направления с ними. Тогда в новой системе координат точки Л и В будут иметь координаты А [0, 0] и Б 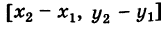. Отсюда на основании формулы (1) получаем

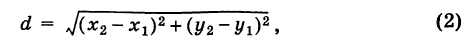
т. е. расстояние между двумя точками плоскости (при любом их расположении) равно корню квадратному из суммы квадратов разностей одноименных координат этих точек.

Замечание. Формула (2) дает также длину отрезка АВ. Легко определить направление этого отрезка. Из прямоугольного А ABC имеем

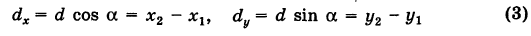
(dx и dy называются проекциями отрезка АВ на оси координат Оху). Отсюда получаем 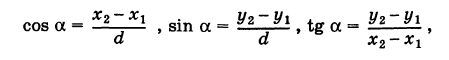где d определяется формулой (2).

Пример:

Танк на местности переместился из точки А (-30, 80) в точку Б (50, 20) (относительно некоторой системы координат Оху)> причем координаты точек даны в километрах. Найти путь d, пройденный танком, если он двигался, не меняя направления.

Решение:

Применяя формулу (2), имеем

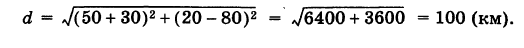
Деление отрезка в данном отношении

Предположим, что отрезок АВ (рис. 8), соединяющий точки A (xl9 уг) и В (x2t у2), разделен точкой С на два отрезка АС и СБ, причем отношение АС к СБ равно I (I > 0):

Требуется выразить координаты х и у точки С(х, у) через координаты концов отрезка АВ.

Опустим перпендикуляры 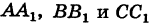соответственно из точек А, В и С на ось Ох. Тогда получим, что три параллельные прямые 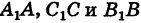пересекают стороны угла (не обозначенного на рисунке), образованного прямыми АВ и Ох. Как известно из элементарной геометрии, пучок параллельных прямых рассекает стороны угла на пропорциональные части; поэтому

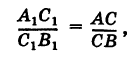
откуда на основании равенства (1) будем иметь

Из рис. 8 видно, что 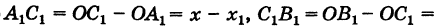х2 – х. Подставляя эти выражения в формулу (2), получим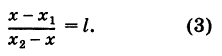

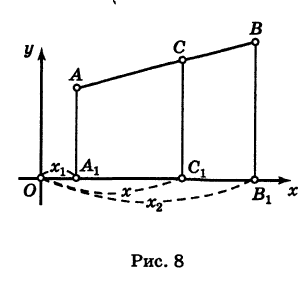
Решая уравнение (3) относительно неизвестной абсциссы х, будем иметь

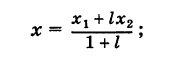
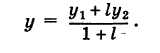Итак, координаты точки С (ху у), делящей отрезок АВ в отношении / (считая от А к В), определяются формулами 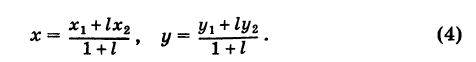Если точка С делит отрезок АВ пополам, то АС = СВ и, следовательно, I = АС/СВ = 1. Обозначая координаты середины отрезка АВ через х, у, получим на основании формул (4)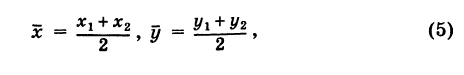

т. е. координаты середины отрезка равны полусуммам соответствующих координат его концов.

Примечание. При выводе формул (4) и (5) мы предполагали, что концы А и В отрезка АВ лежат в первом квадранте и, следовательно, координаты точек Аи В положительны. Легко доказать, что формулы (4) и (5) будут справедливы и в случае произвольного расположения отрезка АВ на координатной плоскости.

Пример:

Вычислить координаты точки С (х, у)> делящей отрезок АВ между точками А (-5, -3) и В (4, -6) в отношении АС/СВ = 3/2.

Решение:

В этом случае I = 3/2 и, следовательно,

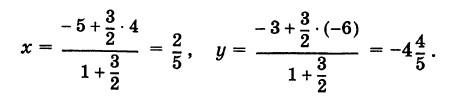
Площадь треугольника

Пусть требуется найти площадь S треугольника ABC (рис. 9) с вершинами

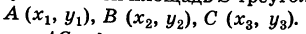
Пусть АВ = с, АС = Ь, а углы, образованные этими сторонами с осью Ох, соответственно равны .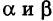

На основании (см. замечание) имеем (рис. 9)

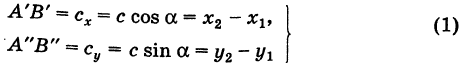
и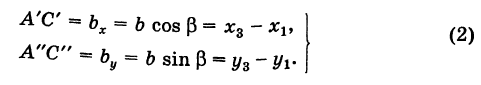

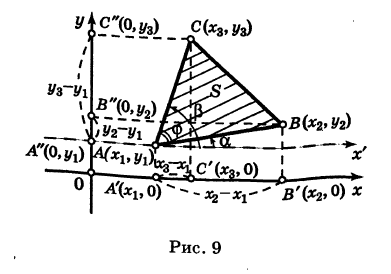
Пусть 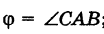; очевидно (рис. 9), 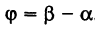. По известной формуле тригонометрии получаем

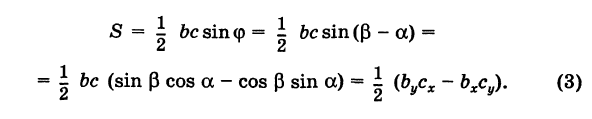
Отсюда в силу (1) и (2) имеем

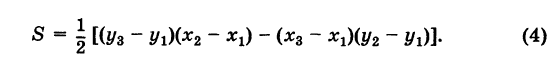
Заметим, что формула (4) при ином расположении вершин может дать площадь треугольника S со знаком минус. Поэтому формулу для площади треугольника обычно пишут в виде

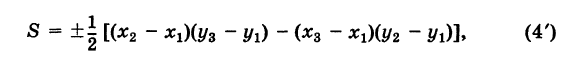
где знак выбирается так, чтобы для площади получалось положительное число,

Используя понятие определителя второго порядка

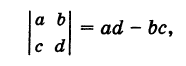
формулу (4′) можно записать в удобной для запоминания форме:

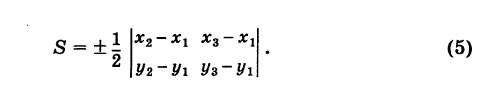
Формула (4′) упрощается, если точка А 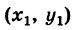находится в начале координат. А именно, полагая 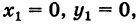получим

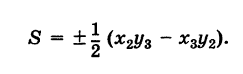
Отметим, что если точки А, В, С находятся на одной прямой, то площадь S = 0; и обратно, если S = 0, то вершины А, Б и С расположены на одной прямой.

Пример:

Вспаханное поле имеет форму треугольника с вершинами А (-2, -1), В (3, 5) и С (-1, 4) (размеры даны в километрах). Определить площадь S этого поля.

По формуле (5) имеем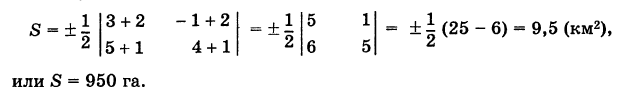

Замечание. Вычисление площади многоугольника сводится к вычислению площадей треугольников. Для этого достаточно разбить многоугольник на треугольники, площади которых вычисляют по формуле (4).

Рекомендую подробно изучить предметы:

Математика Алгебра Линейная алгебра Векторная алгебра Высшая математика Дискретная математика Математический анализ Математическая логика

Ещё лекции с примерами решения и объяснением:

• Линии второго порядка
• Полярные координаты
• Непрерывность функции
• Уравнения поверхности и линии в пространстве
• Интегрирование рациональных дробей
• Интегрирование тригонометрических функций
• Интегрирование тригонометрических выражений
• Интегрирование иррациональных функций

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

[spoiler title=”источники:”]

http://mathhelpplanet.com/static.php?p=onlain-reshit-treugolnik

http://www.evkova.org/pryamougolnaya-sistema-koordinat-na-ploskosti

[/spoiler]

Площадь треугольника, построенного на векторах: онлайн-калькулятор

Формула площади треугольника заложена в программе и вычисляет половину модуля векторного произведения:

S=12·c

Чтобы найти площадь треугольника, необходимы задать значения двух векторов или координаты вершин треугольника. После этого вы получите готовое решение с пояснениями и ответ. Сервис используют школьники, их родители, студенты, преподаватели.

Как найти площадь треугольника, построенного на векторах

Онлайн-калькулятор позволяет учащимся готовиться к занятиям, разбираться в непонятной теме, тренироваться на примерах. Расчеты производятся бесплатно, поэтому вы сможете сэкономить деньги на репетиторе и самостоятельно осваивать материал. Моментальное решение также поможет сдать зачет или экзамен, написать контрольную на хорошую оценку. Родители смогут быстро проверить домашнее задание ребенка, а преподаватели – автоматизировать процесс создания обучающих материалов.

Чтобы вычислить площадь треугольника через векторы, программа выполняет следующие действия:

• Анализирует введенные данные. Если указаны координаты точек, рассчитываются векторы a и b.
• Находит произведение векторов.
• Вычисляет модуль вектора.
• Делит результат на 2 и выдает ответ.

С помощью нашего сайта вы сможете изучить, как найти площадь треугольника не только по векторам, но и другими способами. Мы разделили калькуляторы по темам для удобного использования. Так вы быстро найдете нужную тему и получите правильный ответ. В автоматических расчетах исключена потеря данных между действиями, опечатки. Благодаря калькулятору вы сможете сравнить решение с собственным и найти ошибку.