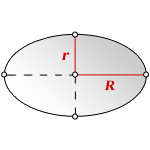
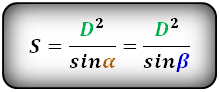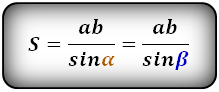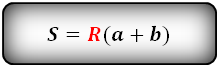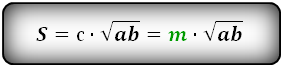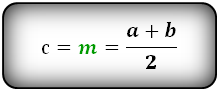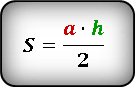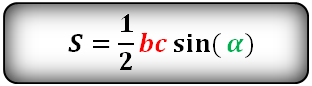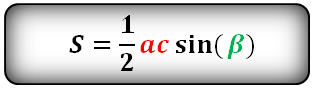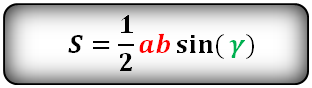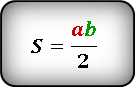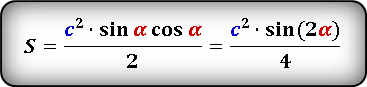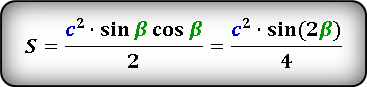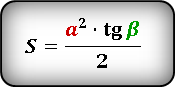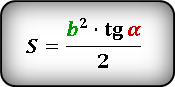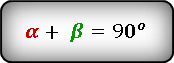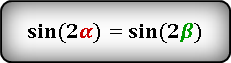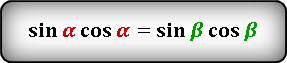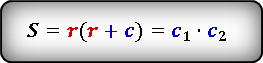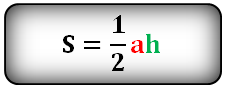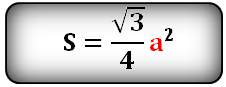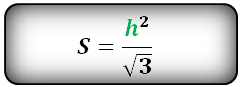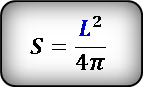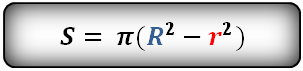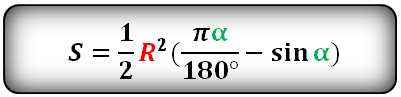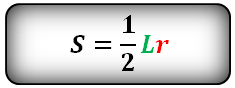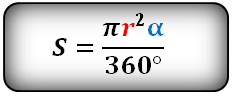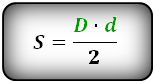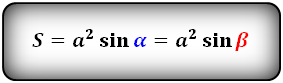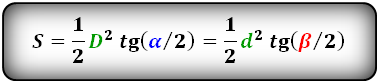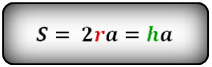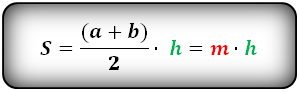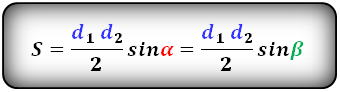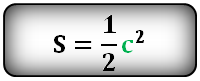Как найти площадь треугольника синус косинус тангенс - Сайт, где вы сможете решить свои вопросы

R – большая полуось

r – малая полуось

π ≈ 3.14

Формула площади эллипса, через полуоси:

Калькулятор, вычислить площадь элипса:

1. Формула площади равнобедренной трапеции через стороны и угол

а – нижнее основание

b – верхнее основание

с – равные боковые стороны

α – угол при нижнем основании

Формула площади равнобедренной трапеции через стороны, (S ):

Формула площади равнобедренной трапеции через стороны и угол, (S ):

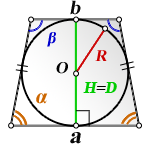
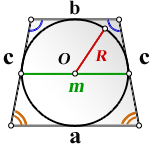
2. Формулы площади равнобедренной трапеции если в нее вписана окружность

R – радиус вписанной окружности

D – диаметр вписанной окружности

O – центр вписанной окружности

H – высота трапеции

α, β – углы трапеции

а – нижнее основание

b – верхнее основание

Формула площади равнобедренной трапеции через радиус вписанной окружности, (S ):

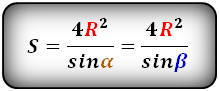
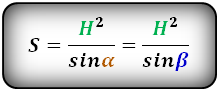
СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:

R – радиус вписанной окружности

m – средняя линия

O – центр вписанной окружности

c – боковые стороны

а – нижнее основание

b – верхнее основание

Формула площади равнобедренной трапеции через радиус вписанной окружности, стороны и среднюю линию (S ):

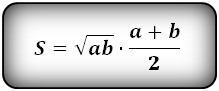
СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:

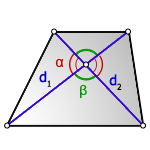
3. Формула площади равнобедренной трапеции через диагонали и угол между ними

d – диагональ трапеции

α, β – углы между диагоналями

Формула площади равнобедренной трапеции через диагонали и угол между ними, (S ):

4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании

c – боковая сторона

m – средняя линия трапеции

α, β – углы при основании

Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):

5. Формула площади равнобедренной трапеции через основания и высоту

a – нижнее основание

b – верхнее основание

h – высота трапеции

Формула площади равнобедренной трапеции через основания и высоту, (S ):

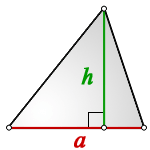
Треугольник это плоская фигура, которая имеет три стороны и три угла. Сумма всех трех углов, равна 180 градусов.
Высота треугольника это – опущенный перпендикуляр из вершины угла на противоположенную сторону или ее продолжение, которую в этом случае, называют основанием.

Что бы найти площадь треугольника,

для этого надо основание умножить на высоту и разделить на два

1. Площадь разностороннего треугольника

h – высота треугольника

a – основание

Формула площади треугольника (S):

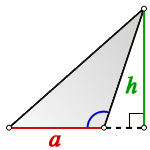
2. Площадь треугольника с тупым углом

h – высота треугольника

a – основание

Формула площади треугольника с тупым углом (S):

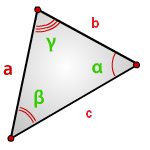
Формулы для треугольника:

Зная у треугольника

две стороны и синус угла между ними, находим по формуле, его площадь

a, b, c – стороны треугольника

α, β, γ – углы

Формулы площади треугольника, через две стороны и угол между ними, (S):

Калькулятор – вычислить, найти площадь треугольника:

Формулы для треугольника:

Сторона произвольного треугольника

Стороны равнобедренного треугольника

Стороны прямоугольного треугольника

Высота произвольного треугольника

Высота прямоугольного треугольника

Высота, медиана, биссектриса равнобедренного треугольника

Высота=медиана=биссектриса равностороннего треугольника

Биссектриса произвольного треугольника

Биссектриса прямоугольного треугольника

Медиана произвольного треугольника

Медиана прямоугольного треугольника

Все разделы по геометрии

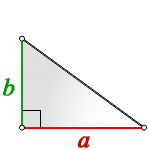
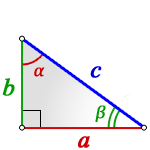
Прямоугольный треугольник, так же как и любой другой треугольник, имеет три стороны и три угла. Разница только в том, что один угол прямой, т. е. 90 градусов и два остальных, острых угла в сумме составляют, тоже 90 градусов.
Две стороны, которые формируют прямой угол, называют катетами, а третья сторона напротив прямого угла, называется – гипотенуза

1. Если известны только катеты

a, b – катеты треугольника

Формула площади треугольника через катеты ( S ) :

2. Если известны острый угол и гипотенуза или катет

c – гипотенуза

a, b – катеты

α, β – острые углы

Формулы площади прямоугольного треугольника через гипотенузу и угол ( S ) :

Формулы площади прямоугольного треугольника через катет и угол ( S ) :

Как известно, сумма острых углов в прямоугольном треугольнике равна 90 градусов, а если

то справедливы следующие тождества:

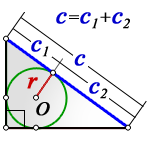
3. Если известны радиус вписанной окружности и гипотенуза

c – гипотенуза

c₁, c₂ – отрезки полученные делением гипотенузы, точкой касания окружности

r – радиус вписанной окружности

О – центр вписанной окружности

Формулы площади прямоугольного треугольника через радиус вписанной окружности и гипотенузу ( S ) :

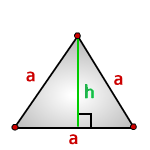
Если вы знаете сторону или высоту

вы можете найти площадь равностороннего треугольника

a – сторона треугольника

h – высота

Площадь треугольника через сторону a и высоту h, (S):

Площадь треугольника только через сторону a, (S):

Калькулятор для расчета площади равностороннего треугольника

Площадь треугольника только через высоту h, (S):

Калькулятор для расчета площади равностороннего треугольника

a – сторона треугольника

h – высота

Формулы для треугольника:

Круг это плоская фигура, все точки которой, расположены на любом расстоянии от определенной точки (центр круга) но не больше заданной длины (радиус).
Радиус круга – отрезок, соединяющий центр окружности и любую, максимально удаленную от центра точку круга.
Диаметр круга – отрезок, соединяющий две любые точки максимально удаленные от центра круга и проходящий через этот центр. Диаметр, в два раза больше радиуса

Зная диаметр

или радиус круга или длину окружности, можно найти его площадь.

r – радиус круга

D – диаметр круга

π ≈ 3.14

Формула площади круга, (S):

Решения задач

на тему: Площадь круга

Калькулятор для расчета площади круга через радиус

Калькулятор для расчета площади круга через диаметр

L – длина окружности

О – центр круга

π ≈ 3.14

Формула площади круга если известна длина окружности, (S):

Решения задач

на тему: Площадь круга

Калькулятор для расчета площади круга через длину

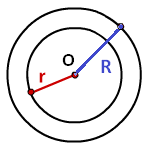
Площадь кольца равна – число π, умноженное на разницу квадратов, радиуса внешней окружности и радиуса внутренней окружности

R – радиус внешней окружности

r – радиус внутренней окружности

π ≈ 3.14

Формула площади кольца (S):

Калькулятор – вычислить, найти площадь кольца

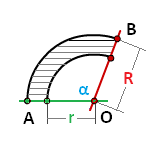
R – радиус внешней окружности

r – радиус внутренней окружности

α – угол сектора AOB, в градусах

π ≈ 3.14

Формула площади сектора кольца (S):

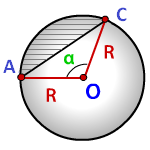
R – радиус круга

α – угол сегмента в градусах

π ≈ 3.14

Формула площади сегмента круга (S), отсекаемая хордой AC:

Калькулятор для расчета длины дуги окружности :

Формулы для окружности и круга:

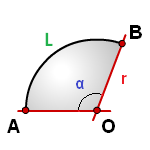
Найти площадь сектора круга если даны радиус и длина дуги или радиус и центральный угол

r – радиус круга

L – длина дуги AB

α – угол сектора круга AOB в градусах

π ≈ 3.14

Формула площади сектора круга (S), через длину дуги (L):

Формула площади сектора круга (S), через угол (α):

Формулы для окружности и круга:

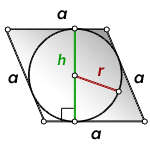
Вычислить площадь ромба, зная: (диагонали) или (сторону и угол между ними) или (диагональ и угол между сторонами)

a – сторона ромба

D – большая диагональ

d – меньшая диагональ

α – острый угол

β – тупой угол

Формулы площади ромба через диагонали и углы между сторонами ( S ):

a – сторона ромба

h – высота

r – радиус вписанной окружности

Формула площади ромба через высоту или радиус вписанной окружности ( S ):

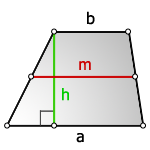
1. Формула площади трапеции через основания и высоту

a – нижнее основание

b – верхнее основание

m – средняя линия

h – высота трапеции

Формула площади трапеции, (S ):

2. Формула площади трапеции через диагонали и угол между ними

d₁, d₂ – диагонали трапеции

α, β – углы между диагоналями

Формула площади трапеции, (S ):

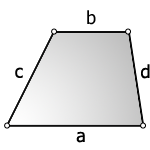
3. Формула площади трапеции через четыре стороны

a – нижнее основание

b – верхнее основание

c , d – боковые стороны

Формула площади трапеции, (S ):

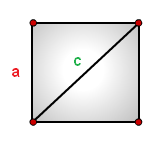
Зная сторону

или диагональ квадрата, можно найти его площадь

a – сторона квадрата

c – диагональ

Формула площади квадрата через сторону a, (S):

Калькулятор – вычислить, найти площадь квадрата:

Формула площади квадрата через диагональ c, (S):

Зная длину

и ширину прямоугольника, можно вычислить его площадь

b – длина прямоугольника

a – ширина прямоугольника

Формула площади прямоугольника, (S):

Калькулятор – вычислить, найти площадь прямоугольника:

a – сторона многоугольника

n – количество сторон

Формула площади правильного многоугольника, (S):

Калькулятор – вычислить, найти площадь правильного многоугольника

Источник

I. Площадь треугольника через синус

Если в задаче даны длины двух сторон треугольника и угол между ними, то можно применить формулу площади треугольника через синус.

Пример расчета площади треугольника через синус. Даны стороны a = 3, b = 4, и угол γ= 30°. По таблице синусов синус угла в 30° равен 0.5

Площадь треугольника будет равна 3 кв. см.

Калькулятор нахождения площади треугольника через синус

Сторона a=	Сторона b=	Угол γ °
Ответ: Площадь треугольника = 3.000

Также могут быть и другие условия. Если дана длина одной стороны и углы, то для начала нужно вычислить недостающий угол. Т.к. сумма всех углов треугольника равняется 180°, то:

$alpha={180^circ}-(beta+gamma)$
$beta={180^circ}-(alpha+gamma)$
$gamma={180^circ}-(alpha+beta)$

Площадь будет равна половине квадрата стороны, умноженной на дробь. В ее числителе находится произведение синусов прилегающих углов, а в знаменателе синус противолежащего угла. Теперь рассчитываем площадь по следующим формулам:

$S= {1/2} * {a^2} * {{ sin{beta} * sin{gamma} } / { sin{alpha} }}$
$S= {1/2} * {b^2} * {{ sin{alpha} * sin{gamma} } / { sin{beta} }}$
$S= {1/2} * {c^2} * {{ sin{alpha} * sin{beta} } / { sin{gamma} }}$

Например, дан треугольник со стороной a=3 и углами γ=60°, β=60°. Вычисляем третий угол: $alpha={180^circ}-({60^circ}+{60^circ})$
Подставляем данные в формулу $S= {1/2} * {3^2} * {{ sin{60^circ} * sin{60^circ} } / { sin{60^circ} }}={1/2} * 9 * {{ 0.86 * 0.86 } / { 0.86 }}=3.87$
Получаем, что площадь треугольника равняется 3,87 кв. см.

II. Площадь треугольника через косинус

Чтобы найти площадь треугольника, нужно знать длины всех сторон. По теореме косинусов можно найти не известные стороны, а уже потом использовать формулу Герона.
По теореме косинусов квадрат неизвестной стороны треугольника равняется сумме квадратов остальных сторон минус удвоенное произведение этих сторон на косинус угла, находящегося между ними.
${c^2}={a^2}+{b^2}-2*a*b*cos{gamma}$
Из теоремы выводим формулы для поиска длины неизвестной стороны:

$a=sqrt{ {c^2}+{b^2}-2*c*b*cos{alpha} }$
$b=sqrt{ {a^2}+{c^2}-2*a*c*cos{beta} }$
$c=sqrt{ {a^2}+{b^2}-2*a*b*cos{gamma} }$

Зная как найти недостающую сторону, имея две стороны и угол между ними можно легко посчитать площадь. Формула площади треугольника через косинус помогает легко и быстро найти решение различных задач.

Пример расчета формулы площади треугольника через косинус
Дан треугольник с известными сторонами a = 3, b = 4, и углом γ= 45°. Для начала найдем недостающую сторону с. По таблице косинусов косинус 45°=0,7. Для этого подставим данные в уравнение, выведенное из теоремы косинусов. $c=sqrt{ {3^2}+{4^2}-2*3*4*cos{45^circ} }=sqrt{ 9+16-2*3*4*0.7 }=sqrt{ 25-16.97 }=2.83$
Теперь используя формулу, найдем площадь треугольника по трем сторонам:

Калькулятор нахождения площади треугольника через косинус

Сторона a=	Сторона b=	Угол γ °
Ответ: Площадь треугольника = 4.243

Источник

Синус, косинус и тангенс острого угла прямоугольного треугольника

Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.

Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.

Острый угол — меньший 90 градусов.

Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин 🙂

Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается C. Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается .

Угол A обозначается соответствующей греческой буквой alpha .

Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.

Катеты — стороны, лежащие напротив острых углов.

Катет , лежащий напротив угла alpha , называется противолежащим (по отношению к углу alpha ). Другой катет , который лежит на одной из сторон угла alpha , называется прилежащим.

Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:

sin A $=genfrac{}{}{}{0}{displaystyle a}{displaystyle c}.$

Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:

cos A $=genfrac{}{}{}{0}{displaystyle b}{displaystyle c}.$

Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:

tg A $=genfrac{}{}{}{0}{displaystyle a}{displaystyle b}.$

Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:

tg A $=genfrac{}{}{}{0}{displaystyle sin A}{displaystyle cos A}.$

Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):

ctg A $=genfrac{}{}{}{0}{displaystyle cos A}{displaystyle sin A}.$

Обратите внимание на основные формулы для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.

sin $displaystyle alpha = frac{a}{c}$	sin ${}^2 alpha +$ cos $displaystyle {}^2 alpha =1$	$alpha + beta = 90 ^{circ}$
cos $displaystyle alpha = frac{b}{c}$	1+tg $displaystyle {}^2 alpha =frac{1}{cos ^2 alpha}$	cos = sin
tg $displaystyle alpha = frac{a}{b}$	1+ctg $displaystyle {}^2 alpha =frac{1}{sin ^2 alpha}$	sin = cos
ctg $displaystyle alpha = frac{b}{a}$		tg = ctg

Давайте докажем некоторые из них.

Сумма углов любого треугольника равна $180^{circ}$ . Значит, сумма двух острых углов прямоугольного треугольника равнa $90^{circ}$ .
С одной стороны, $sin A =genfrac{}{}{}{0}{displaystyle a}{displaystyle c}$ как отношение противолежащего катета к гипотенузе. С другой стороны, $cos B =genfrac{}{}{}{0}{displaystyle a}{displaystyle c}$ , поскольку для угла катет а будет прилежащим. Получаем, что . Иными словами, $cos left( 90^{circ}-A right) = sin A$ .
Возьмем теорему Пифагора: . Поделим обе части на получаем $displaystyle left ( frac{a}{c} right )^2+left ( frac{b}{c} right )^2=left ( frac{c}{c} right )^2 ,$ то есть
Мы получили основное тригонометрическое тождество.
Поделив обе части основного тригонометрического тождества на , получим: $1+tg ^2 A = genfrac{}{}{}{0}{displaystyle 1}{displaystyle cos ^2 A }.$ Это значит, что если нам дан тангенс острого угла , то мы сразу можем найти его косинус. Аналогично, $1+ctg ^2 A =genfrac{}{}{}{0}{1}{sin ^2 A }.$

Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?

Мы знаем, что сумма углов любого треугольника равна $180^{circ}$ .

Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: .

Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?

С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.

Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.

Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от $0^{circ}$ до $90^{circ}$ .

	0	$genfrac{}{}{}{0}{displaystyle pi}{displaystyle 6}$	$genfrac{}{}{}{0}{displaystyle pi}{displaystyle 4}$	$genfrac{}{}{}{0}{displaystyle pi}{displaystyle 3}$	$genfrac{}{}{}{0}{displaystyle pi}{displaystyle 2}$
sin	0	$displaystyle frac{1}{2}$	$displaystyle frac{sqrt{2}}{2}$	$displaystyle frac{sqrt{3}}{2}$
cos		$displaystyle frac{sqrt{3}}{2}$	$displaystyle frac{sqrt{2}}{2}$	$displaystyle frac{1}{2}$	0
tg	0	$genfrac{}{}{}{0}{displaystyle 1}{displaystyle sqrt{3}}$			−
ctg	−			$genfrac{}{}{}{0}{displaystyle 1}{displaystyle sqrt{3}}$	0

Обратите внимание на два прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.

Докажем теорему:

Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.

В самом деле, пусть АВС и — два прямоугольных треугольника с прямыми углами С и C_1 и равными острыми углами А и A_1.

Треугольники АВС и подобны по первому признаку подобия треугольников, поэтому $displaystyle frac{AB}{A_1 B_1}=frac{BC}{B_1 C_1}=frac{AC}{A_1 C_1 } .$

Из этих равенств следует, что $displaystyle frac{BC}{AB}=frac{B_1 C_1}{A_1 B_1} ,$ т. е. sin А = sin A_1.

Аналогично, $displaystyle frac{AC}{AB}=frac{A_1C_1}{A_1 B_1},$ т. е. cos А = cos A_1, и $displaystyle frac{BC}{AC}=frac{B_1C_1}{A_1 C_1},$ т. е. tg A = tg A_1.

Это значит, что синус, косинус и тангенс зависят только от величины угла.

Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.

Задача 1. В треугольнике ABC угол C равен $90^{circ}$ , sin A = 0,1. Найдите cos B.

Задача решается за четыре секунды.

Поскольку $A+B = 90^{circ}$ , sin A = cos B = 0,1.

Задача 2. В треугольнике ABC угол равен $90^{circ}$ , AB=5 , $sin A = genfrac{}{}{}{0}{displaystyle 7}{displaystyle 25}$ .

Найдите .

Решение:

$sin A = genfrac{}{}{}{0}{displaystyle a}{displaystyle c} = genfrac{}{}{}{0}{displaystyle BC}{displaystyle AB} = genfrac{}{}{}{0}{displaystyle 7}{displaystyle 25}.$

Отсюда

$BC= genfrac{}{}{}{0}{displaystyle 7}{displaystyle 25} cdot AB = genfrac{}{}{}{0}{displaystyle 7}{displaystyle 5}.$

Найдем AC по теореме Пифагора.

$AC=sqrt{AB^2-BC^2} = genfrac{}{}{}{0}{displaystyle 24}{displaystyle 5} = 4,8.$

Ответ: 4,8.

Задача 3. В треугольнике АВС угол С равен AВ = 13, ВС = 5. Найдите косинус и тангенс острого угла А. Ответ округлите до сотых.

Решение:

Для угла А противолежащий катет – это ВС,

АВ является гипотенузой треугольника, лежит против Значит, sin A $displaystyle = frac{BC}{AB}= frac{5}{13}.$

Катет, прилежащий к angle A – это катет АС, следовательно, cos⁡ А $displaystyle = frac{AC}{AB}=frac{AC}{13}.$

Длину катета АС найдем по теореме Пифагора:

Тогда $AC = sqrt{AB^2-BC^2}=sqrt{(13)^2-5^2}=sqrt{144}=12.$

cos⁡ А $displaystyle = frac{12}{13}=0,923 ... approx 0,92 ;$

tg A $displaystyle = frac{BC}{AC} = frac{5}{12}=0,416...approx 0,42.$

Ответ: 0,92; 0,42.

Заметим, что если катеты прямоугольного треугольника равны 5 и 12, то гипотенуза равна 13. Это одна из так называемых Пифагоровых троек. О них мы расскажем в других статьях сайта.

Задача 4. В треугольнике АВС угол С равен AC = 2, sin A= $displaystyle frac{sqrt{17}}{17} .$

Найдите BC.
Решение:

AC = b = 2, BC = a, AB = c.

Так как sin A $displaystyle = frac{a}{c} = frac{BC}{AB} = frac{sqrt{17}}{17},$ $displaystyle frac{a}{c} = frac{sqrt{17}}{17} ,$ $displaystyle c = frac{17a}{sqrt{17}}=sqrt{17}a.$

По теореме Пифагора получим

$a^2+2^2=(sqrt{17} a)^2;$

$displaystyle a= frac{1}{2}=0,5;$

Ответ: 0,5.

Задача 5. В треугольнике АВС угол С равен AC = 4, tg A = $displaystyle frac{33}{4sqrt{33}} .$ Найдите AB.

Решение:

AC = b = 4, tg A $displaystyle = frac{a}{b}=frac{33}{4sqrt{33}},$

$displaystyle frac{a}{4}=frac{33}{4sqrt{33}},$ $displaystyle a=frac{4 cdot 33}{4 cdot sqrt{33}}=sqrt{33},$

$AB = c = sqrt{a^2+b^2}=sqrt{(sqrt{33})^2+4^2}=sqrt{33+16} =7.$

Ответ: 7.

Задача 6.

В треугольнике АВС угол С равен CH – высота, AB = 13, tg A = $displaystyle frac{1}{5} .$ Найдите AH.

Решение:

AВ = с = 13, tg A = $displaystyle frac{a}{b}=frac{1}{5} ,$ тогда b = 5a.

По теореме Пифагора ABC:

$displaystyle a=sqrt{frac{169}{26}}=frac{13}{sqrt{26}},$ тогда $displaystyle b = 5a=5cdot frac{13}{sqrt{26}}=frac{65}{sqrt{26}}.$

(по двум углам), следовательно $displaystyle frac{AH}{AC}=frac{AC}{AB} ,$ откуда

$displaystyle AH = frac{AC^2}{AB}=frac{b^2}{c}=left ( frac{65}{sqrt{26}}right )^2:13=12,5.$

Ответ: 12,5.

Задача 7. В треугольнике АВС угол С равен

CH – высота, BC = 3, sin A = $displaystyle frac{1}{6} .$

Найдите AH.

Решение:

Так как sin A = $displaystyle frac{a}{c} = frac{BC}{AB} = frac{1}{6},$ тогда $displaystyle frac{3}{c} = frac{1}{6} ,$ c = АВ = 18.

sin A = $displaystyle frac{a}{c}$ = cos⁡ B = $displaystyle frac{1}{6} .$

Рассмотрим BHC:

${cos B= }displaystyle frac{BH}{BC}$ = $displaystyle frac{1}{6} ,$ получим $displaystyle frac{BH}{3}=displaystyle frac{1}{6},$

тогда BH = $displaystyle frac{3}{6}=displaystyle frac{1}{2}$ = 0,5,

AH = AB – BH = 18 – 0,5 = 17,5.

Ответ: 17,5.

Задача 8. В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, BC = 3, cos A = $displaystyle frac{sqrt{35}}{6}.$

Найдите АH.

Решение:

Так как для АВС: cos A = $displaystyle frac{AC}{AB}=$ sin В = $displaystyle frac{sqrt{35}}{6},$

а для ВНС: sin В = $displaystyle frac{CH}{BC}$ = $displaystyle frac{sqrt{35}}{6}$ , откуда СН = $displaystyle frac{BC cdot sqrt{35}}{6}=displaystyle frac{3 cdot sqrt{35}}{6}=displaystyle frac{sqrt{35}}{2},$

По теореме Пифагора найдем ВН:

$BH = sqrt{{BC}^2-{CH}^2}=sqrt{3^2-{left(displaystyle frac{sqrt{35}}{2}right)}^2}=$

$=sqrt{9-displaystyle frac{35}{4}}=sqrt{displaystyle frac{1}{4}}=displaystyle frac{1}{2}=0,5.$

Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой. Поэтому для АВС получим:

${CH}^2=AH cdot BH,$ тогда $AH= displaystyle frac{ {CH}^2}{BH}, ; AH= displaystyle frac{ {left(displaystyle frac{sqrt{35}}{2}right)}^2}{0,5}=displaystyle frac{35 cdot 2}{4}=17,5.$

Ответ: 17,5.

Задача 9. В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, СН = 24 и BН = 7. Найдите sin A.

Решение:

По определению sin A= $displaystyle frac{a}{c}$ = $displaystyle frac{BC}{AB}$ =

Рассмотрим BHC : ${cos B= }displaystyle frac{BH}{BC}.$

ВС найдем по теореме Пифагора:

ВС= $sqrt{{BH}^2+{CH}^2}=sqrt{7^2+{24}^2}=sqrt{49+576}=sqrt{625}=25,$

тогда ${cos B= }displaystyle frac{BH}{BC}=displaystyle frac{7}{25}=0,28,$ а значит и sin A = = 0,28.

Ответ: 0,28.

Задача 10. В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, СН = 8 и BН = 4. Найдите tg A.

Решение:

По определению sin A = $displaystyle frac{a}{c}$ = $displaystyle frac{BC}{AB}$ = cos A = $displaystyle frac{b}{c}$ = $displaystyle frac{AC}{AB}$ =

тогда tg A = $displaystyle frac{sin A}{{cos A }}=displaystyle frac{cosB}{sinB}=ctgB,$ который найдем из BHC:

$ctgB=displaystyle frac{BH}{CH}=displaystyle frac{4}{8}=0,5.$

Ответ: 0,5.

Задача 11. В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, BН = 12, tg A = $displaystyle frac{2}{3}.$ Найдите АН.

Решение:

По определению tg A= $displaystyle frac{BC}{AC}=ctgB=displaystyle frac{2}{3}.$

Для BHC: $ctgB=displaystyle frac{BH}{CH}=displaystyle frac{2}{3}$ , значит $displaystyle frac{12}{CH}=displaystyle frac{2}{3},$ СН = $displaystyle frac{12 cdot 3}{2}=18.$

Для АHC: tg A= $displaystyle frac{CH}{AH}=displaystyle frac{2}{3},$ то $displaystyle frac{18}{AH}=displaystyle frac{2}{3},$ AH = $displaystyle frac{18 cdot 3}{2}=27.$

Ответ: 27.

Задача 12. В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, BН = 12, sin A = $displaystyle frac{2}{3}.$ Найдите АВ.

Решение:

Так как cos В = $displaystyle frac{BC}{AB}$ = sin A = $displaystyle frac{2}{3}.$

Из СВН имеем cos В = $displaystyle frac{HB}{BC}$ = $displaystyle frac{2}{3},$ тогда ВС = $displaystyle frac{3 cdot HB}{2}=displaystyle frac{3 cdot 12}{2}=18.$

В АВС имеем sinA = $displaystyle frac{BC}{AB}$ = $displaystyle frac{2}{3},$ тогда AВ = $displaystyle frac{3 cdot BC}{2}=displaystyle frac{3 cdot 18}{2}=27.$

Ответ: 27.

Задача 13. В треугольнике АВС угол С равен 90 ${}^circ,$ из вершины прямого угла к гипотенузе проведена высота СН. Найдите cos A, AC и AB, если СН = 12, ВС = 20.

Решение:

Найдем НВ по теореме Пифагора из ВСН:

$HB = sqrt{BC^2-BH^2}=sqrt{20^2-12^2}=sqrt{(20-12)(20+12)}=$

sin В = $displaystyle frac{CH}{BC}$ = $displaystyle frac{12}{20}=displaystyle frac{3}{5}.$

Для АВС: cos A = $displaystyle frac{AC}{AB}=sin B=displaystyle frac{3}{5},$ получили cos A = 0,6.

Найдем АС и АВ несколькими способами.

1-й способ.

Так как cos A = $displaystyle frac{AC}{AB}=displaystyle frac{3}{5},$ то пусть АС = 3х, АВ = 5х,

тогда по теореме Пифагора ${AC}^2+{BC}^2= {AB}^2,$ получим ${(3x)}^2+{(20)}^2= {(5x)}^2$
${25x}^2-{9x}^2= {20}^2 ,$

${16x}^2= {20}^2,$

$x^2= {left(displaystyle frac{20}{4}right)}^2,$
х = 5 ( так как х0). Значит,

2-й способ.

(по двум углам), значит $displaystyle frac{HB}{CB}=frac{HC}{AC}=frac{BC}{AB}$ или $displaystyle frac{16}{20}={12}{AC}={20}{AB} = k,$

k = $displaystyle frac{16}{20}=displaystyle frac{4}{5} ,$ тогда $displaystyle frac{12}{AC}=displaystyle frac{4}{5},$ АС = $displaystyle frac{12 cdot 5}{4}=15$ ; $displaystyle frac{20}{AB}=displaystyle frac{4}{5},$ АВ = $displaystyle frac{20 cdot 5}{4}=25.$

3-й способ.

${CH}^2=AH cdot HB$ (высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой) , тогда ${12}^2=AH cdot 16,$ АН = 144:16 = 9.

АВ = АН + НВ = 9 + 16 = 25.

По теореме Пифагора найдем АС:

$AC = sqrt{{AB}^2-{BC}^2}=sqrt{{25}^2-{20}^2}=sqrt{(25-20)(25+20)}$ =

Ответ: cos A = 0,6; АС = 15, АВ = 25.

Задача 14.

Высота ВН прямоугольного треугольника АВС, проведенная из вершины прямого угла В, равна 24 и отсекает от гипотенузы АС отрезок НС, равный 18.

Найдите АВ и cos А.

Решение:

Из прямоугольного ВНС по теореме Пифагора найдем гипотенузу ВС и cos C:

ВС = $sqrt{{HC}^2+{BH}^2}=sqrt{{18}^2+{24}^2}=sqrt{324+576}$ =

cos C = $displaystyle frac{HC}{BC}=displaystyle frac{18}{30}=displaystyle frac{3}{5}.$

Для АВС: sin А = $displaystyle frac{BC}{AC}$ = cos C = $displaystyle frac{3}{5}.$

Для АНВ: sin А = $displaystyle frac{BH}{AB}$ = $displaystyle frac{3}{5},$ то $displaystyle frac{24}{AB}$ = $displaystyle frac{3}{5},$ АВ = $displaystyle frac{24 cdot 5}{3}=40.$

Из основного тригонометрического тождества найдем

cos A = $sqrt{1-{sin}^2A}=sqrt{1-0,36}=sqrt{0,64}=0,8.$

Ответ: АВ = 40, cos A = 0,8.

Задача 15.

Гипотенуза АС прямоугольного треугольника АСЕ равна 50, sin А = $displaystyle frac{7}{25}.$

Найдите площадь треугольника.

Решение:

В прямоугольном АСЕ sin А = $displaystyle frac{CE}{AC},$

значит $displaystyle frac{7}{25}$ = 14.

Второй катет найдем, используя теорему Пифагора: $AE= sqrt{{AC}^2-{CE}^2};$

$AE = sqrt{{50}^2-{14}^2}=sqrt{(50-14)(50+14)} =sqrt{36cdot 64}=6cdot8=48.$

Площадь прямоугольного треугольника равна S = $displaystyle frac{1}{2}ab,$

поэтому $S_{ACE}= displaystyle frac{1}{2} AEcdot CE=displaystyle frac{48cdot 14}{2}=336.$

Ответ: 336.

Задача 16.

В треугольнике АВС угол С — прямой, катеты АВ = 13 и ВС = 12, СК — высота.

Найдите sin Результат округлите до сотых.

Решение:

A-общий, $angle AKC=angle ACB=90{}^circ$ ),

значит sin $angle ACK=displaystyle frac{AK}{AC}=displaystyle frac{AC}{AB}.$

Найдем АС по теореме Пифагора из САВ:

$AC = sqrt{{AB}^2-{BC}^2}=sqrt{{13}^2-{12}^2}=$

Тогда sin $angle ACK=displaystyle frac{5}{13}=0,384..approx 0,38.$

Ответ: 0,38.

Задача 17. В треугольнике АВС АС = ВС, АВ = 72, cos A = $displaystyle frac{12}{13}.$ Найдите высоту СН.

Решение:

Так как АС = ВС, то АВС — равнобедренный с основанием АВ, тогда

высота СН является медианой, то есть АН = НВ = $displaystyle frac{1}{2}AB=36.$

Поскольку АСН — прямоугольный,

cos A = $displaystyle frac{AH}{AC}=$ $displaystyle frac{12}{13},$ то есть $displaystyle frac{36}{AC}=$ $displaystyle frac{12}{13}$ АС = $displaystyle frac{36 cdot 13}{12}=39.$

По теореме Пифагора ${AH}^2+{CH}^2={AC}^2,$ тогда

$CH = sqrt{{AC}^2-{AH}^2} = sqrt{{39}^2-{36}^2}=$

Ответ: 15.

Задача 18. В треугольнике АВС угол С равен 90 ${}^circ,$ sin A = $displaystyle frac{11}{14},$ AC = 10 Найдите АВ.

Решение:

1-й способ.

Поскольку sin A = $displaystyle frac{BC}{AB}=$ $displaystyle frac{11}{14},$ то можно обозначить

ВС = 11х, АВ = 14х.

По теореме Пифагора $AC^2+{BC}^2={AB}^2;$

${(10sqrt{3})}^2+{(11x)}^2={(14x)}^2;$

${(14x)}^2-{(11x)}^2 = 3 cdot 100;$

(14х- 11х)(14х + 11х) = 3 cdot 100;

x^2=4, учитывая, что длина стороны положительна, х = 2,

следовательно, АВ = 14 cdot 2 = 28.

2-й способ.

Воспользуемся основным тригонометрическим тождеством ${sin}^2A+{cos}^2A=1;$

cos A = $sqrt{1-{sin}^2A}=sqrt{1-{left(displaystyle frac{11}{14}right)}^2}=sqrt{displaystyle frac{196-121}{196}}=sqrt{displaystyle frac{75}{196}}=displaystyle frac{5sqrt{3}}{14}.$

По определению cos A = $displaystyle frac{AC}{AB},$ значит $displaystyle frac{AC}{AB}= displaystyle frac{5sqrt{3}}{14}.$

Так как АС=10 то $displaystyle frac{10sqrt{3}}{AB}= displaystyle frac{5sqrt{3}}{14},$ откуда АВ = $displaystyle frac{10sqrt{3} cdot 14}{5sqrt{3}}$ = 28.

Ответ: 28.

Задача 19. Найдите углы ромба АВСD, если его диагонали АС и ВD равны 4 sqrt{3} и 4.

Решение:

Пусть angle ВАО = alpha .

Диагонали ромба делят его углы пополам, значит, = alpha .

Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам, следовательно, в прямоугольном треугольнике АВО катет АО = $displaystyle frac{1}{2} AC=2sqrt{3},$ а катет ВО = $displaystyle frac{1}{2}BD =2.$

Поэтому tg $alpha =displaystyle frac{BO}{AO}=displaystyle frac{2}{2sqrt{3}}=displaystyle frac{1}{sqrt{3}},$ откуда $alpha =30{}^circ .$

$angle BAD=2alpha =60{}^circ , ; angle ADC=angle ABC=180{}^circ -60{}^circ =120{}^circ .$

Ответ: ${60}^circ,$ ${120}^circ,$ ${60}^circ,$ ${120}^circ .$

Часто в задачах встречаются треугольники с углами $90^{circ},, 30^{circ}$ и $60^{circ}$ или с углами $90^{circ},, 45^{circ}$ и $45^{circ}$ . Основные соотношения для них запоминайте наизусть!

Для треугольника с углами $90^{circ},, 30^{circ}$ и $60^{circ}$ катет, лежащий напротив угла в $30^{circ}$ , равен половине гипотенузы.

Треугольник с углами $90^{circ},, 45^{circ}$ и $45^{circ}$ — равнобедренный. В нем гипотенуза в sqrt{2} раз больше катета.

Задача 20.

В треугольнике АВС угол С равен 90 ${}^circ,$ угол А равен 30 ${}^circ,$ АВ = 2

Найдите высоту CH.

Решение:

Рассмотрим АВС:

По свойству катета, лежащего против угла ${30}^circ,$ имеем ВС = $displaystyle frac{1}{2}$ АВ =

В BHC: $angle BHC=90{}^circ ,; angle B=60{}^circ ,$ то $angle HCB=30{}^circ ,$ следовательно, ВН = $displaystyle frac{1}{2}$ BC = $displaystyle frac{sqrt{3}}{2}.$

По теореме Пифагора найдем НС:

$HC = sqrt{{BC}^2-{BH}^2}=sqrt{{left(sqrt{3}right)}^2-{left(displaystyle frac{sqrt{3}}{2}right)}^2}=sqrt{3-displaystyle frac{3}{4}}=$

$=sqrt{2displaystyle frac{1}{4}}=sqrt{displaystyle frac{9}{4}}=displaystyle frac{3}{2}=1,5.$

Ответ: 1,5.

Задача 21.

В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, АВ = 2, $angle A=30{}^circ .$ Найдите АH.

Решение:

Из АВС найдем ВС = $displaystyle frac{1}{2}$ АВ = 1 (по свойству катета, лежащего против угла 30 ${}^circ$ ),

$angle A=30{}^circ ,$ то $angle B=60{}^circ .$

Из ВСН: $angle BHC=90{}^circ , angle B=60{}^circ ,$ то $angle HCB=30{}^circ ,$ следовательно,

ВН = $displaystyle frac{1}{2}$ ВС = $displaystyle frac{1}{2}.$

АН = АВ — НВ = 2 – $displaystyle frac{1}{2}$ = 1,5.

Ответ: 1,5.

Еще раз повторим, что такое синус, косинус и тангенс угла в прямоугольном треугольнике.

Как запомнить эти соотношения? Лучший способ – решать много задач, и на уроках геометрии, и готовясь к ЕГЭ. Тогда все формулы, равенства, соотношения запомнятся сами собой.

Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.

Если вам понравился разбор данной темы – записывайтесь на курсы подготовки к ЕГЭ по математике онлайн

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Синус, косинус и тангенс острого угла прямоугольного треугольника» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

План урока:

Тригонометрические функции тупых углов

Вычисление координат точки

Вычисление площади треугольника

Площадь параллелограмма

Теорема синусов

Теорема косинусов

Тригонометрические функции тупых углов

Впервые с тригонометрическими функциями мы познакомились в 8 классе. Определить их значение можно было с помощью прямоугольного треугольника, рассматривая отношения его сторон (катетов и гипотенуз). Но такой способ определения тригонометрических функций подходит только для острых углов, попадающих в интервал от 0 до 90°. Оказывается, есть способ для вычисления значений тригонометрических функций и от больших углов.

Построим на координатной плоскости полуокружность, центр которой располагается в начале координат, а радиус равен единице. Ее называют единичной полуокружностью. Проведем из точки (0; 0) луч под некоторым углом α, который пересечет полуокружность в некоторой точке М с координатами (х; у). Заметим, что каждому значению α соответствует своя точка М на единичной полуокружности:

Опустим из М перпендикуляр на ось Ох в некоторую точку D. Тогда, если угол α острый,получается прямоугольный треугольник МOD, длины сторон которого можно определить так:

Получается, что координаты точки M как раз и являются синусом и косинусом угла α. Логично считать, что если α – не острый угол, то всё равно координаты точки M будут определять синус и косинус угла α.

Видно, что при тупом угле α точка М оказывается левее оси Оу, поэтому ее абсцисса становится отрицательной. Получается, что косинус может принимать отрицательные значения.

С помощью единичной полуокружности несложно выяснить значения синусов и косинусов для углов 0°, 90° и 180°. Они соответствуют координатам точек А, В и С на рисунке:

Так как эти точки имеют координаты (1; 0), (0; 1) и (– 1; 0), то можно записать следующее:

Используя это определение, найдем тангенс для углов 0° и 180°:

Заметим, что для 90° использовать эту формулу не удастся, так как это приведет к делению на ноль. Поэтому считается, что для 90° значение тангенса не определено, то есть его нельзя вычислить.

Единичная полуокружность является дугой окружности, чей радиус равен единице, а центр находится в начале координат. То есть она может быть задана уравнением

Тем самым мы доказали, что это тождество, которое показывает связь тригонометрических функций друг с другом, выполняется не только для острых углов, но и для всех углов из диапазона 0° ≤α ≤ 180°.

Для вычисления значений тригонометрических углов тупых углов удобно пользоваться так называемыми формулами приведения. Их довольно много, и изучаются они в основном в 10 классе, нам же хватит всего двух формул:

Например, пусть надо вычислить синус для угла 120°. Для этого мы представляем угол в виде разности, где в качестве уменьшаемого используется угол 180°:

Убедиться в справедливости этих двух формул приведения можно с помощью такого построения:

Точка М соответствует углу α, а точка K – углу (180° – α). Опустим из этих точек перпендикуляры МС и KD. Так как

Получается, что ∆OKD и ∆ОМС – прямоугольные, у них есть одинаковый острый угол α, и их гипотенузы ОК и ОМ также одинаковы как радиусы одной окружности. Тогда эти треугольники равны, и поэтому

Знак минус в первом из этих равенств показывает, что точки K отрицательная абсцисса. В итоге мы доказали две формулы приведения.

Задание. Вычислите sin 150°.

Решение. Представим угол 150° в виде разности:

Вычисление координат точки

Пусть есть некоторая точка А(х;у) с неотрицательной ординатой. Соединим ее с началом координат прямой, которая образует угол α с осью Ох. Посмотрим, как связаны координаты А со значением α.

Пусть луч ОА пересечет единичную окружность в точке М. Опустим из М и А перпендикуляры на Ох, в точки Н и С соответственно. Теперь сравним ∆ОМН и ∆ОАС. Они прямоугольные, и у них есть одинаковый угол α, следовательно, они подобны. Коэффициент подобия можно найти, поделив ОА на ОМ, при этом учтем, что ОМ = 1, так как М лежит на единичной полуокружности:

Примечание. Данное доказательство не рассматривает частные случаи, когда точка А лежит непосредственно на осях Ох и Оу, и тогда подобные треугольники ∆ОМН и ∆ОАС построить не удается. Эти случаи можно рассмотреть отдельно и показать, что для них выведенные формулы также справедливы.

Задание. Точка А находится на расстоянии 3 от начала координат (точки О), причем луч ОА образует с осью Ох угол 135°. Найдите координаты точки А.

Решение. Используя выведенные формулы, мы можем записать:

Вычисление площади треугольника

В 8 классе мы уже познакомились с одной из формул для определения площади треугольника. Однако на практике возникают ситуации, когда удобнее использовать другие формулы, одну из которых мы сейчас выведем.

Пусть в произвольном ∆АВС известны две стороны, например, ВС (обозначим ее буквой а) и АС (ее обозначим как b). Также известна величина угла между ними:

Разместим этот треугольник в системе координат так, чтобы точка С совпала с началом координат, в находилась на оси Ох и имела положительную абсциссу, А располагалась в первой четверти:

В этом случае координаты А будут определяться формулами:

Найдите площадь ∆МКН.

Решение.

Задание. Используя калькулятор, найдите площадь треугольника со сторонами 14 и 7 см, если угол между ними равен 48°. Ответ округлите до десятых долей см².

Решение. Подставляя числа в формулу, получаем:

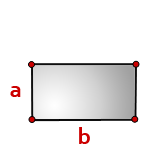
Задание. Диагонали прямоугольника пересекаются под углом 30°, причем они равны 10 см. Вычислите площадь этого прямоугольника.

Решение.

Заметим, что диагонали прямоугольника при пересечении образуют не один, а два угла. Пусть в прямоугольнике АВСD диагонали пересекаются в точке О, и ∠АОВ = 30°. Тогда можно найти ∠ВОС, ведь он смежный с ∠АОВ:

Чтобы найти площадь прямоугольника, мы можем найти площади 4 треугольников, из которых он состоит, и потом сложить их. Для каждого из этих треугольников нам известны две стороны (они составляют по 5 см) и угол между ними:

Площадь параллелограмма

Из выведенной нами формулы площади треугольника вытекает и новая формула для площади параллелограмма. Пусть в параллелограмме нам известны смежные и угол между ними:

На рисунке смежные стороны АВ и AD обозначены буквами a и b, а угол между ними обозначен как α. Проведем диагональ BD. Площадь ∆ABD можно вычислить:

Задание. Стороны параллелограмма имеют длины 8 и 11 см, а один из углов параллелограмма равен 30°. Какова площадь этого параллелограмма?

Решение. Просто подставляем данные в формулу

Ответ: 44 см².

Задание. Известна площадь параллелограмма MNEF, одна из его сторон и угол:

Так как противоположные стороны в параллелограмме одинаковы, то MF также имеет длину 5:

MF = NE = 5

Запишем формулу для площади и подставим в нее известные данные:

Теорема синусов

Пусть есть некоторый ∆АВС, в котором стороны мы обозначим буквами:

Посчитаем его площадь, используя стороны b и c:

Также площадь треугольника можно выразить через а и с:

Полученная формула показывает, что в каждом треугольнике отношение стороны к синусу противолежащего угла – это константа, не зависящая от выбора стороны. Другими словами,в любом треугольнике стороны пропорциональны синусам углов, которые лежат против них. Это утверждение именуют теоремой синусов.

В большинстве задач достаточно выведенной формулы

Однако можно дополнить теорему синусов, выяснив, чему же именно равны все эти три отношения. Для этого впишем треугольник в окружность, после чего построим диаметр BD:

Пусть радиус этой окружности равен R, тогда диаметр BD будет вдвое больше:

Теперь рассмотрим ∆ВСD. ∠С здесь – прямой, ведь это вписанный угол, опирающийся на полуокружность, то есть дугу в 180°. По определению синуса, которое мы давали ещё в 8 классе, можно записать:

C учетом уже выведенного равенства (6) теорема синусов примет вид:

С помощью теоремы синусов у любого треугольника можно найти две неизвестные стороны, если известны третья сторона и два угла. Процесс нахождение неизвестных элементов треугольника по уже известным элементам именуется решением треугольника. Всего у треугольника 6 элементов – три стороны и три угла. Для нахождения всех элементов в общем случае достаточно знать только 3 из них, а остальные можно найти, используя теорему синусов или иные геометрические соображения.

Задание. Решите треугольник, если одна из его сторон равна 14, а прилегающие к ней углы имеют величину 60° и 40°.

Решение.

Обозначим описанный в условии треугольник как ∆МВК. Пусть МК = 14, ∠М = 60° и∠К = 40°. Тогда нам надо найти ∠В, МВ и ВК. Проще всего найти∠В, ведь в любом треугольнике все углы в сумме дают 180°:

Обратите внимание, что так как углы 40° и 80° не являются табличными, то их значения надо вычислять на калькуляторе, а результат вычисления получается приближенным. В данном случае мы округлили его до сотых.

Осталось найти сторону ВК, это также делается с помощью теоремы синусов:

Задание. В ∆SRT∠S = 30°, ∠R = 45°, а высота RM, опущенная на сторону TS, имеет длину 6. Решите ∆SRT.

Решение.

Теперь надо найти какую-нибудь сторону в ∆SRT. Для этого рассмотрим ∆RMS. Он прямоугольный, а потому для него можно записать:

Для нахождения двух оставшихся сторон можно использовать теорему синусов:

Задание. В параллелограмме MNEF∠MFE составляет 120°, а диагональ NF равна 24 и образует со стороной NE угол 40°. Найдите длину МN и MF.

Решение.

Далее заметим, что ∠FNE и ∠MFN одинаковы, ведь они накрест лежащие при параллельных отрезках NE и MF и секущей NF:

Теперь в ∆MNF известна сторона NF и все три угла. Это позволяет с помощью теоремы синусов найти и остальные две стороны:

Задание. В окружности радиусом 5 построен вписанный угол величиной 30°. Определите длину хорды, на которую он опирается.

Решение.

Решение. По теореме синусов мы можем записать, что

Теорема косинусов

Теорема синусов помогает решать треугольники, в которых известны хотя бы два угла, а также одна из сторон. Но что делать в случае, если наоборот, даны две стороны, но только один угол? Здесь необходима другая теорема, которую именуют теоремой косинусов.

Возьмем произвольный треугольник со сторонами а, b и c и поместим его на координатной плоскости так, как показано на рисунке:

Обозначим угол между а и b как α. Тогда координаты А будут определяться так:

Точка В в свою очередь будет иметь координаты (а; 0). Зная координаты А и В, мы можем найти квадрат расстояния между ними, то есть величину с²:

Полученное соотношение как раз и является теоремой косинусов.

Данная формула позволяет находить третью сторону треугольника, если известны две другие, а также угол между ними. Однако ее можно переписать так, чтобы с ее помощью можно было вычислять косинус угла, зная все три стороны треугольника:

Это позволяет решать те треугольники, для которых теоремы синусов недостаточно.

Легко заметить, что теорема косинусов похожа на теорему Пифагора. Более того, если угол α = 90°, то формула теоремы косинусов превращается в теорему Пифагора, которая, таким образом, является ее частным случаем. По этой причине иногда теорему косинусов именуют обобщенной теоремой Пифагора.

Задание. Решите ∆MNE, если

Решение. По теореме косинусов находим сторону NE:

Осталось найти ∠N и ∠Е. Для этого запишем теорему косинусов так, чтобы в ней фигурировал ∠N:

Мы нашли cosN. Чтобы вычислить сам ∠N, следует использовать особую функцию на калькуляторе или компьютере, которая называется арккосинусом и является обратной для операции «извлечение косинуса». Более подробно она изучается уже в 10 классе. С ее помощью мы узнаем, что

Обратите внимание, что обычно калькулятор выдает результат, показывая десятые и сотые доли градусы, не переводя их в минуты и секунды. Можно оставить ответ и в таком виде. При желании перевести сотые доли в минуты следует дробную часть умножить на 60:

Задание. На различных сторонах угла∠А, равного 45°, отложены точки В и С так что

Задание. Решите треугольник, если его стороны имеют длину 14, 18 и 20.

Решение.

Решение. Здесь надо дважды применить теорему косинусов, чтобы найти какие-нибудь два угла в ∆АВС:

∠C также можно найти через теорему косинусов, но проще просто вычесть из 180° два уже вычисленных угла:

Во всех рассмотренных задачах на решение треугольника мы знали три элемента треугольника и по ним однозначно вычисляли три других элемента. Однако иногда это невозможно. Так, если в задаче помимо двух сторон указан угол, который НЕ лежит между ними, то в итоге задача может иметь два решения.

Задание. В ∆MNE ∠M составляет 60°, а стороны МЕ и NE имеют длины 10 и 9 соответственно. Какова длина MN?

Решение. Теорему синусов здесь применить не удастся, так как для нее необходимо знать хотя бы два угла. Поэтому остается только записать теорему косинусов так, чтобы в ней использовался ∠M:

Получили квадратное уравнение, решить его можно через дискриминант:

В рамках данного урока мы узнали про теоремы синусов и косинусов и научились использовать их для решения треугольников. Также мы познакомились с новыми формулами для вычисления площадей треугольника и параллелограмма.

Источник

Здравствуйте, уважаемые читатели. В этой статье рассмотрим задачи по геометрии за 9 класс. Они встречаются в 15 задании ОГЭ по математике.

Теорема

Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

Задача №1

Теорема о площади треугольника (9 класс). Задание №15 ОГЭ

Решение

Ответ 50

Задача №2

Решение

Введем обозначения для треугольника. Назовем его АВС

Против угла лежит соответствующая ему сторона. Как показано на рисунке.

Запишем формулу нахождения площади треугольника опираясь на теорему о площади треугольника.

По условию дан равнобедренный треугольник. Значит сторона с=а.

Выпишем из условия задачи известные данные:

Подставим в формулу, получаем

Чтобы найти значение Sin120, воспользуемся формулой приведения.

Объяснение формулы приведения: Возьмем единичную окружность. Введем обозначения; SinA – это У, CosА – это Х. Откладываем всегда угол, начиная с координаты (1,0). Выполняем два действия: 1) Определяем знак. Откладываем угол в 120 градусов, оказываемся во второй четверти. Во второй четверти значение Sin120 имеет знак “+”. 2) Выясняем изменится ли SinA на CosA или CosA на SinA. Изменения происходят только в том случае, если в разложении угла имеется 90 градусов. Если возьмем другое разложение Sin(180-60)=Sin60 (Четверть вторая, но при 180 градусов изменения SinA на CosA не происходят)

Ответ 4.

Задача №3

Решение

Найдем второй острый угол прямоугольного треугольника:

Вспомним свойство прямоугольного треугольника: В прямоугольном треугольнике катет лежащий против угла в 30 градусов равен половине гипотенузы.

Запишем формулу нахождения площади треугольника опираясь на теорему о площади треугольника.

Выпишем из условия задачи известные данные:

Подставим в формулу, получаем:

Отсюда найдем значение Х

Нашли сторону b – катет прямоугольного треугольника, лежащий против угла в 30 градусов. По заданию нужно найти гипотенузу. Тогда

Ответ 80

Спасибо, что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог

Источник

1. Площадь разностороннего треугольника

2. Площадь треугольника с тупым углом

I. Площадь треугольника через синус

II. Площадь треугольника через косинус

Синус, косинус и тангенс острого угла прямоугольного треугольника

Тригонометрические функции тупых углов

Вычисление координат точки

Вычисление площади треугольника

Площадь параллелограмма

Теорема синусов

Теорема косинусов

Вам также может понравиться

Как составить таблицу значение грибов 5 класс биология

Как при пароле найти таблицу символов

Как найти плейлисты в youtube

Добавить комментарий Отменить ответ