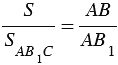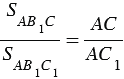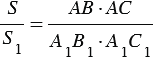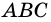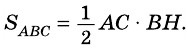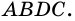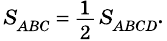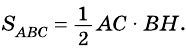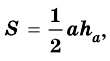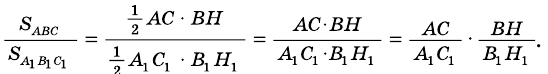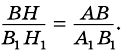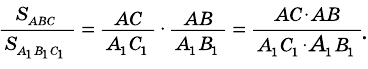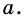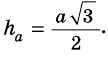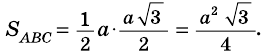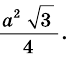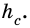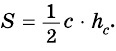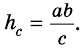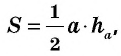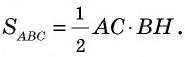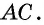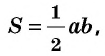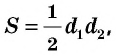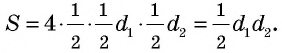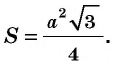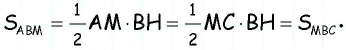- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Площадь
- Площадь треугольника
Одну из сторон треугольника часто называют основанием. Если основание выбрано, то под словом “высота” подразумевают высоту треугольника, проведенную к основанию.
Теорема
Площадь треугольника равна половине произведения его основания на высоту
Доказательство
Дано: 

Доказать: S = 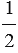

Доказательство:
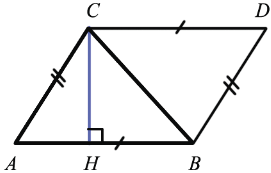
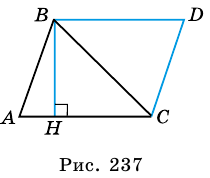
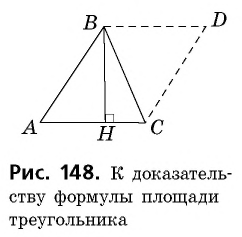
Достроим данный треугольник до параллелограмма ABCD так, как показано на рисунке. 


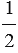

Следствие 1
Следствие 2
Если высоты двух треугольников равны, то их площади относятся как основания
Теорема
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы
Доказательство
Дано: 



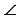
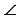
Доказать: 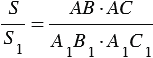
Доказательство:
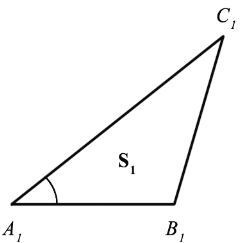
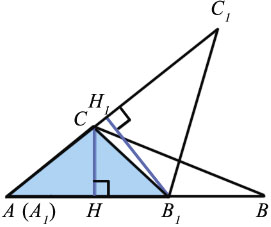
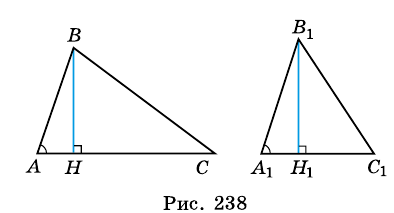
Наложим треугольник А1В1С1 на треугольник АВС так, чтобы вершина А1 совместилась с вершиной А, а стороны А1В1 и А1С1 наложились соответственно на лучи АВ и АС.
Треугольники АВС и АВ1С имеют общую высоту СН, поэтому
Треугольники АВ1С и АВ1С1 также имеют общую высоту – В1Н1, поэтому
Перемножая полученные равенства, находим:
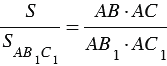
Теорема доказана.
Советуем посмотреть:
Понятие площади многоугольника
Площадь квадрата
Площадь прямоугольника
Площадь параллелограмма
Площадь трапеции
Теорема Пифагора
Теорема, обратная теореме Пифагора
Формула Герона
Площадь
Правило встречается в следующих упражнениях:
7 класс
Задание 492,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 12,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 515,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 571,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 598,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 842,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 867,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1136,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1241,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1277,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Площадь треугольника:
Теорема (о площади треугольника). Площадь треугольника равна половине произведения его стороны на высоту, к ней проведенную.
Доказательство:
Пусть
Докажем, что
1) Проведем через вершину 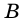
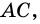
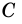
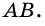
2) 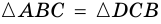
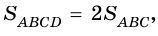
3) Так как 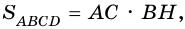
В общем виде формулу площади 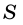
где 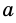
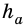
Следствие 1. Площадь прямоугольного треугольника равна половине произведения катетов.
Следствие 2. Если сторона одного треугольника равна стороне другого треугольника, то площади таких треугольников относятся как их высоты, проведенные к этим сторонам.
Следствие 3. Если высота одного треугольника равна высоте другого треугольника, то площади этих треугольников относятся как стороны, к которым проведены эти высоты.
Пример:
Докажите, что если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, образующих этот угол.
Доказательство:
Рассмотрим 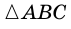
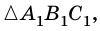
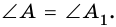
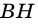
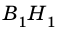
1) Имеем:
2) 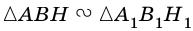
3) Имеем:
Пример:
Найдите площадь равностороннего треугольника, сторона которого равна
Решение:
Пусть 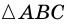
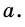
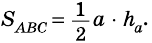
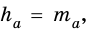
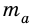
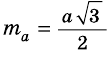
Следовательно,
Ответ.
Пример:
Стороны треугольника равны 8 см, 15 см и ^ 17 см. Найдите высоту треугольника, проведенную к его наибольшей стороне.
Решение:
Так как 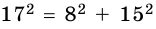
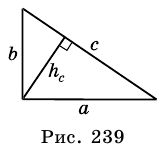
Пусть на рис. 239 изображен прямоугольный треугольник, у которого 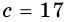
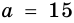
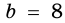
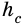
Площадь этого треугольника можно найти
по формулам: 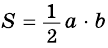
Тогда 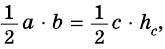
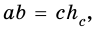
Таким образом, имеем: 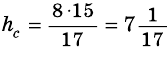
Ответ. 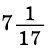
Теорема (формула площади треугольника)
Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне:
где 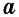
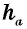
Доказательство:
Пусть 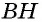
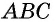
Проведем через вершины 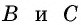
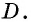
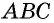
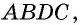
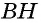
По формуле площади параллелограмма 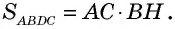
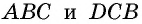
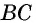
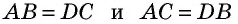
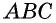
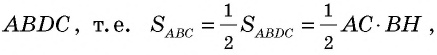
Следствие 1
Площадь прямоугольного треугольника равна половине произведения его катетов:
где 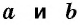
Действительно, в прямоугольном треугольнике высота, проведенная к катету, совпадает с другим катетом.
Следствие 2
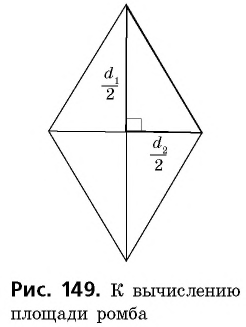
Площадь ромба равна половине произведения его диагоналей:
где 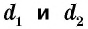
Действительно, диагонали делят ромб на четыре равных прямоугольных треугольника с катетами 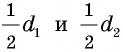
Следствие 3
Площадь равностороннего треугольника со стороной 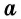
Обоснуйте это следствие самостоятельно.
Опорная задача
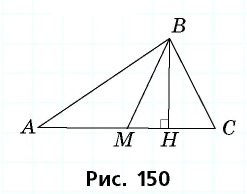
Медиана делит треугольник на два равновеликих треугольника. Докажите.
Решение:
Пусть 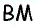
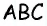
Проведем высоту 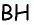
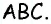
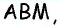
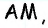
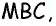
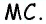
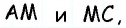
Эта задача имеет интересные обобщения: если высоты двух треугольников равны, то отношение площадей этих треугольников равно отношению их оснований; если основания двух треугольников равны, то отношение площадей этих треугольников равно отношению их высот.
Докажите эти утверждения самостоятельно.
- Соотношения между сторонами и углами произвольного треугольника
- Окружность и круг
- Описанные и вписанные окружности
- Плоские и пространственные фигуры
- Взаимное расположения прямых на плоскости
- Треугольник
- Решение треугольников
- Треугольники и окружность
Здравствуйте, уважаемые читатели. В этой статье рассмотрим задачи по геометрии за 8-9 класс. Задачи на нахождение площади треугольника. Они встречаются в 15 задании ОГЭ по математике.
В статье будут рассмотрены несколько формул вычисления площади треугольника.
Первая теорема
Площадь треугольника равна половине произведения его высоты на сторону, к которой она проведена.
Задача №1
Сторона треугольника равна 16, а высота, проведённая к этой стороне, равна 19. Найдите площадь этого треугольника
Решение
Задача №2
У треугольника со сторонами 2 и 10 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 5. Чему равна высота, проведённая ко второй стороне?
Решение
Площадь треугольника равна половине произведения его высоты на сторону, к которой она проведена. Поэтому площадь треугольника в каждом случае будет одинаковой.
Задача №3
На стороне AC треугольника ABC отмечена точка D так, что AD=6, DC=10. Площадь треугольника ABC равна 48. Найдите площадь треугольника BCD.
Решение
Если на стороне треугольника взята точка, которая делит эту сторону в отношении m:n, то отрезок, соединяющий эту точку с вершиной противолежащего угла, делит треугольник на два треугольника, площади которых относятся как m:n:
Отрезок AD относиться к отрезку DC как 6:10. Значить площадь треугольника ABD составляет 6 частей от площади треугольника АВС, а площадь треугольника DBC – 10 частей. Вся площадь треугольника ABC равна 16 частей. По условию площадь треугольника АВС равна 48. Значит площадь треугольника ВСD=(48/16)*10=30.
Ответ 30
Задача №4
Два катета прямоугольного треугольника равны 4 и 10. Найдите площадь этого треугольника.
Решение
Вторая теорема
Площадь прямоугольного треугольника равна половине произведения его катетов.
Ответ 20
Задача №5
В прямоугольном треугольнике один из катетов равен 4, а угол, лежащий напротив него равен 45°. Найдите площадь треугольника
Решение:
Если в прямоугольном треугольнике, один из острых углов равен 45 градусам, то и второй острый угол равен 45 градусам, так как сумма острых углов в прямоугольном треугольнике равна 90 градусов. Если в треугольнике два угла равны, то этот треугольник равнобедренный.
Значит в треугольнике катеты равны 4 ( a=b=4). Найдем площадь равнобедренного прямоугольного треугольника:
Ответ 8
Задача №6
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 8 и 17.
Решение
Вспомним что такое катет и гипотенуза.
Стороны прямоугольного треугольника, которые образуют прямой угол, называются катеты, а третья сторона – гипотенуза.
Чтобы вычислить площадь прямоугольного треугольника, необходимо вычислить второй катет. Для этого воспользуемся теоремой Пифагора.
Теорема Пифагора
Квадрат гипотенузы равен сумме квадратов катетов.
Зная оба катета прямоугольного треугольника, вычислим его площадь:
Ответ 60
Задача №7
Катеты прямоугольного треугольника равны 21 и 72. Найдите высоту, проведенную к гипотенузе.
Решение
В этой задаче, чтобы найти высоту, проведенную к гипотенузе, необходимо воспользоваться двумя формулами нахождения площади треугольника. Первая формула (для прямоугольного треугольника): половина произведения его катетов. Вторая формула: половина произведения высоты на сторону, к которой эта высота проведена. Площадь, вычисленная разными формулами одной фигуры, одинаковая. Для решения, нам понадобятся размеры гипотенузы. Вычислим ее:
Теперь найдем, чему будет равна высота:
Ответ 20,16
Задача №8
Боковая сторона равнобедренного треугольника равна 25, а основание равно 48. Найдите площадь этого треугольника.
Решение.
В этой задаче, площадь треугольника найдем по формуле Герона. Для этого нужно знать полупериметр (периметр, деленный на 2) треугольника и длину каждой стороны.
В равнобедренном треугольнике, боковые стороны равны. Найдем периметр треугольника. Периметр треугольника – это сумма всех длин сторон треугольника
Ответ 168
Задача №9
В прямоугольном треугольнике гипотенуза равна 82, а один из острых углов равен 45°. Найдите площадь треугольника.
Решение
Если в прямоугольном треугольнике, один из острых углов равен 45 градусам, то и второй острый угол равен 45 градусам, так как сумма острых углов в прямоугольном треугольнике равна 90 градусов. Если в треугольнике два угла равны, то этот треугольник равнобедренный.
В нашем случает получается треугольник прямоугольный и равнобедренный т.е. катеты треугольника равны. Найдем катеты прямоугольного треугольника через теорему Пифагора.
Пусть катеты прямоугольного треугольника это Х
Ответ 1681
Задача №10
Решение
Третья теорема. Теорема о площади треугольника (9 класс)
Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
Ответ 50
Спасибо, что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог
Комментарии преподавателя
Повторение темы «Площадь». Решение задач
1. Повторение теоретической части главы «Площадь»
Вначале уделим внимание тому, что вспомним все основные теоремы, формулы и факты, полученные нами при изучении главы «Площадь», и акцентируем внимание на их особенностях. Затем рассмотрим сложный пример на комплексное применение нескольких из упомянутых фактов, касающихся площадей фигур.
1. Площадь квадрата равна квадрату его стороны (см. Рис. 1). 
Рис. 1. Квадрат
2. Площадь прямоугольника равна произведению его сторон (см. Рис. 2). 
Рис. 2. Прямоугольник
3. Площадь параллелограмма равна произведению основания на опущенную на него высоту (см. Рис. 3). 
Рис. 3. Параллелограмм
4. Площадь произвольного треугольника равна половине произведения основания на опущенную на него высоту (см. Рис. 4). 
Рис. 4. Произвольный треугольник
5. Площадь прямоугольного треугольника равна половине произведения катетов (см. Рис. 5). 
Рис. 5. Прямоугольный треугольник
6. Если у двух треугольников высоты равны (

Рис. 6
7. Медиана треугольника делит его на два равновеликих треугольника (см. Рис. 7). 
Рис. 7
8. Площадь ромба равна половине произведения диагоналей (см. Рис. 8). 
Рис. 8. Ромб
9. Если у двух треугольников равны углы (

Рис. 9
10. Площадь трапеции равна произведению полусуммы ее оснований на высоту (см. Рис. 10). 
Рис. 10. Трапеция
11. Теорема Пифагора. Для прямоугольного треугольника с катетами 



Теорема, обратная теореме Пифагора. Для всякой тройки положительных чисел 



Рис. 11
12. Формула Герона. Применяется для нахождения площади треугольника, если известны длины его сторон (см. Рис. 12). 

Рис. 12
2. Рассмотрение сложного примера
Пример 1. Через вершину прямого угла прямоугольного треугольника с катетами 6 м и 8 м проведен перпендикуляр к гипотенузе. Вычислить площади образовавшихся треугольников.
Решение. Изобразим Рис.13.
Рис. 13
Нам известно: 

Найдем по теореме Пифагора гипотенузу треугольника: 
Для того чтобы в дальнейшем выразить высоту треугольника, вычислим его площадь с помощью катетов: 


Рассмотрим треугольник 





Площадь треугольника 








Ответ: 

ИСТОЧНИК
http://x-uni.com/geometriya/8-klass/video/povtorenie-temy-ploschad
http://metodbook.ru/index.php/matematika/13-testy-po-geometrii-8-klass/96-test-po-geometrii-8-klass-obobshchenie-temy-ploshchad-variant-1.html
http://metodbook.ru/index.php/matematika/13-testy-po-geometrii-8-klass/97-test-po-geometrii-8-klass-obobshchenie-temy-ploshchad-variant-2.html
http://www.uchportal.ru/_ld/105/10586_zad_ploschadi.rar
http://rushkolnik.ru/tw_files2/urls_3/891/d-890061/890061_html_m5ff065f.jpg
http://cs1-48v4.vk-cdn.net/p24/3551abddfac0c8.mp3?extra=amJxaBk9gfTT0lPmsOEwb8Rn_T2twbNJH1OUazYT-T9cSSu4_1787ibMzOu6ytv1rZKrpdEq7XnWZN1f-bjAuKyWIFf7mzw
Прежде, чем
рассматривать вопрос о нахождении площади треугольника, вспомним, что высотой
треугольника называется перпендикуляр, проведённый из вершины треугольника
на противоположную сторону или её продолжение.
Теперь докажем, что
площадь треугольника равна половине произведения длины стороны на высоту,
проведённую к ней.
Доказательство
Пусть –
треугольник.
Докажем, что .
Рассмотрим и
.
,
как
противолеж. стороны ,
–
общая.
по
третьему признаку.
Значит, .
,
,
.
.
.
Что и
требовалось доказать.
Из доказанного
следует, что площадь прямоугольного треугольника равна половине
произведения длин его катетов.
Возьмём некоторый
прямоугольный треугольник ABC.
Катет AC –
это и есть высота, проведённая к стороне BC, которая также является катетом.
А тогда, так как
площадь треугольника равна половине произведения длины стороны на высоту,
проведённую к ней, получаем, что площадь треугольника
, то
есть равняется половине произведения длин катетов рассматриваемого
треугольника.
Также следует, что если
высота одного треугольника равна высоте другого треугольника, то их площади
относятся как длины сторон, к которым проведены высоты.
На рисунке
перпендикуляр BE, проведённый к
прямой AC, является высотой треугольника
ABC и треугольника CBD.
,
.
, то
есть как длины сторон треугольников, к которым проведены высоты.
Теорема. Если угол одного треугольника равен углу другого треугольника, то
площади этих треугольников относятся как произведения сторон, заключающих
равные углы.
Доказательство.
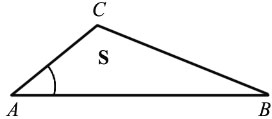
Рассмотрим
треугольники ABC и A1B1C1. Пусть S – площадь
треугольника ABC, а S1 – площадь
треугольника A1B1C1. Углы А и A1 этих треугольников равны.
–
площадь ,
–
площадь .
.
Докажем, что .
,
,
,
.
Таким образом, теорема
доказана.
Закрепим новый
материал на практике.
Задача. Найдите площадь треугольника ,
если длина стороны см,
а высота , проведённая к этой стороне, в два раза её меньше.
Решение.
,
(см).
(см2).
Ответ: см2.
Задача. Вычислите площадь треугольника ,
если высота см,
отрезок см,
а .Решение.
Решение
–
прямоугольный,
так как –
высота.
,
тогда .
Значит, –
равнобедренный, тогда см.
(см).
(см2).
Ответ: см2.
Задача. Найдите длины катетов прямоугольного треугольника, если они относятся
как , а
его площадь равна см2.
Решение.
,
,
,
(см).
(см).
Ответ: см,
см.
Итак, на этом уроке
мы доказали, что площадь треугольника равна половине произведения длины стороны
на высоту, проведённую к ней.
Убедились, что
площадь прямоугольного треугольника равна половине произведения длин его
катетов. А также, что если высота одного треугольника равна высоте другого
треугольника, то их площади относятся как длины сторон, к которым проведены
высоты.
Доказали теорему: если
угол одного треугольника равен углу другого треугольника, то площади этих
треугольников относятся как произведения сторон, заключающих равные углы.
Также мы решили
несколько задач для закрепления изученного материала.