Формулы площади геометрических фигур
Площадь геометрической фигуры – численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Формулы площади треугольника

-
Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты -
Формула площади треугольника по трем сторонам
Формула Герона
S = √p(p – a)(p – b)(p – c)
-
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними. -
Формула площади треугольника по трем сторонам и радиусу описанной окружности
-
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.где S – площадь треугольника,
a, b, c – длины сторон треугольника,
h – высота треугольника,
γ – угол между сторонами a и b,
r – радиус вписанной окружности,
R – радиус описанной окружности,p = a + b + c – полупериметр треугольника. 2
Формулы площади квадрата

-
Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.S = a2
-
Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.где S – площадь квадрата,
a – длина стороны квадрата,
d – длина диагонали квадрата.
Формула площади прямоугольника

Площадь прямоугольника равна произведению длин двух его смежных сторон
S = a · b
где S – Площадь прямоугольника,
a, b – длины сторон прямоугольника.
Формулы площади параллелограмма

-
Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.S = a · h
-
Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.S = a · b · sin α
-
Формула площади параллелограмма по двум диагоналям и углу между ними
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.где S – Площадь параллелограмма,
a, b – длины сторон параллелограмма,
h – длина высоты параллелограмма,
d1, d2 – длины диагоналей параллелограмма,
α – угол между сторонами параллелограмма,
γ – угол между диагоналями параллелограмма.
Формулы площади ромба

-
Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.S = a · h
-
Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.S = a2 · sin α
-
Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.где S – Площадь ромба,
a – длина стороны ромба,
h – длина высоты ромба,
α – угол между сторонами ромба,
d1, d2 – длины диагоналей.
Формулы площади трапеции

-
Формула Герона для трапеции
S = a + b √(p-a)(p-b)(p-a-c)(p-a-d) |a – b| -
Формула площади трапеции по длине основ и высоте
Площадь трапеции равна произведению полусуммы ее оснований на высотугде S – площадь трапеции,
a, b – длины основ трапеции,
c, d – длины боковых сторон трапеции,p = a + b + c + d – полупериметр трапеции. 2
Формулы площади выпуклого четырехугольника

-
Формула площади четырехугольника по длине диагоналей и углу между ними
Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними:
где S – площадь четырехугольника,
d1, d2 – длины диагоналей четырехугольника,
α – угол между диагоналями четырехугольника. -
Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности)
Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности
S = p · r
-

Формула площади четырехугольника по длине сторон и значению противоположных углов
S = √(p – a)(p – b)(p – c)(p – d) – abcd cos2θ
где S – площадь четырехугольника,
a, b, c, d – длины сторон четырехугольника,
p = a + b + c + d2 – полупериметр четырехугольника,
θ = α + β2 – полусумма двух противоположных углов четырехугольника.
-
Формула площади четырехугольника, вокруг которого можно описать окружность
S = √(p – a)(p – b)(p – c)(p – d)
Формулы площади круга

-
Формула площади круга через радиус
Площадь круга равна произведению квадрата радиуса на число пи.S = π r2
-
Формула площади круга через диаметр
Площадь круга равна четверти произведения квадрата диаметра на число пи.где S – Площадь круга,
r – длина радиуса круга,
d – длина диаметра круга.
Формулы площади эллипса
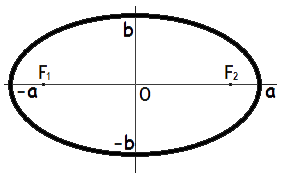
Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи.
S = π · a · b
где S – Площадь эллипса,
a – длина большей полуоси эллипса,
b – длина меньшей полуоси эллипса.
Площади фигур. Основные формулы.
Площадь треугольника.
| Формула | Рисунок | Расшифровка формулы |
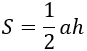 |
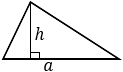 |
а – основание, h – высота, проведенная к этому основанию. Формула применима для любого треугольника. |
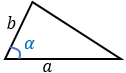 |
a, b – стороны, α – угол между этими сторонами. Формула применима для любого треугольника. |
|
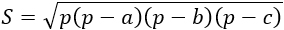 |
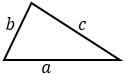 |
a, b, с – стороны, р – полупериметр (сумма трех сторон, деленная пополам). Формула применима для любого треугольника. |
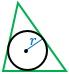 |
r – радиус вписанной в треугольник окружности, р – полупериметр (сумма трех сторон, деленная пополам). Формула применима для любого треугольника. |
|
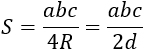 |
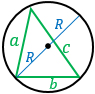 |
a, b, с – стороны, R – радиус описанной около треугольника окружности, d – диаметр описанной окружности. Формула применима для любого треугольника. |
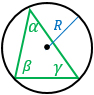 |
R – радиус описанной около треугольника окружности, α, β, γ – углы треугольника. Формула применима для любого треугольника. |
|
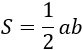 |
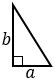 |
a, b – катеты. Формула применима для прямоугольного треугольника. |
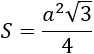 |
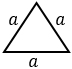 |
a – сторона. Формула применима для равностороннего (правильного) треугольника. |
Площадь квадрата и прямоугольника.
Площадь параллелограмма и ромба.
| Формула | Рисунок | Расшифровка формулы |
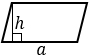 |
а – одна из сторон параллелограмма, h – высота, проведенная к этой стороне | |
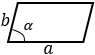 |
а, b – стороны параллелограмма, α – угол между этими сторонами | |
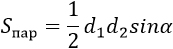 |
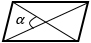 |
d1, d2 – диагонали, α – угол между диагоналями (можно брать любой угол, т.к. синусы смежных углов равны) |
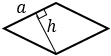 |
а – сторона ромба, h – высота, проведенная к этой стороне | |
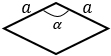 |
а – сторона ромба, α – угол между этими сторонами | |
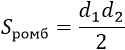 |
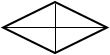 |
d1, d2 – диагонали ромба |
Площадь трапеции.
| Формула | Рисунок | Расшифровка формулы |
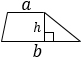 |
а, b – основания трапеции, h – высота. Формула применима для любой* трапеции. |
|
|
m – средняя линия трапеции, h – высота. Формула применима для любой трапеции. |
||
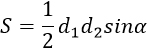 |
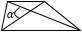 |
d1, d2 – диагонали трапеции, α – угол между диагоналями (можно брать любой угол, т.к. синусы смежных углов равны). Формула применима для любой трапеции. |
*Любая трапеция – это и равнобедренная, и прямоугольная, и тупоугольная, и произвольная 🙂
Площадь круга и кругового сектора.
Площадь многоугольника.
| Формула | Рисунок | Расшифровка формулы |
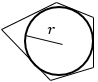 |
р – полупериметр (сумма всех сторон многоугольника, деланная на 2), r – радиус вписанной в этот многоугольник окружности. *Пятиугольник нарисован для примера. Формула работает как для правильного, так и для произвольного многоугольника, главное, чтобы в него можно было вписать окружность. |
1. Формула площади равнобедренной трапеции через стороны и угол

b – верхнее основание
a – нижнее основание
c – равные боковые стороны
α – угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S):

Формула площади равнобедренной трапеции через стороны и угол, (S):



2. Формула площади равнобокой трапеции через радиус вписанной окружности

R – радиус вписанной окружности
D – диаметр вписанной окружности
O – центр вписанной окружности
H – высота трапеции
α, β – углы трапеции
Формула площади равнобокой трапеции через радиус вписанной окружности, (S):

СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:

3. Формула площади равнобедренной трапеции через диагонали и угол между ними

d – диагональ трапеции
α, β – углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):

4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании

m – средняя линия трапеции
c – боковая сторона
α, β – углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):

5. Формула площади равнобедренной трапеции через основания и высоту

b – верхнее основание
a – нижнее основание
h – высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S):

Площадь многоугольника — это величина той части плоскости, которую занимает многоугольник.
Некоторые свойства площади фигур
-
Если многоугольники равны, то они имеют равные площади.
-
Если многоугольник состоит из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.

Рис. (1). Нахождение площади многоугольника
Рассмотрим, как найти площадь у разных фигур.
Площадь квадрата
Площадь квадрата равна квадрату его стороны.
, где
a
— длина стороны квадрата.
Площадь прямоугольника
Площадь прямоугольника равна произведению его длины на ширину (смежные стороны).
, где
a
и
b
— длина и ширина.
Площадь параллелограмма равна произведению основания на высоту.

Рис. (2). Параллелограмм
,
a
(
AD
и
CD
) — основание,
h
(
BE
и
BF
) — высота.
Площадь ромба равна половине произведения его диагоналей.

Рис. (3). Ромб

Рис. (4). Треугольник
Площадь треугольника равна половине произведения основания на высоту.
, где
a
(
AD
) — основание,
h
(
BE
) — высота треугольника.
Площадь прямоугольного треугольника равна половине произведения его катетов.

Рис. (5). Трапеция
Площадь трапеции равна половине суммы оснований, умноженной на высоту.
, где
a
(
BC
) и
b
(
AD
) — основания,
h
(
BE
) — высота.
Площадь круга и кругового сектора

Рис. (6). Круг
— площадь кругового сектора.
Более подробно ознакомиться с примерами можно здесь.
