Здравствуйте, уважаемые читатели. В этой статье рассмотрим задачи по геометрии за 8-9 класс. Задачи на нахождение площади треугольника. Они встречаются в 15 задании ОГЭ по математике.
В статье будут рассмотрены несколько формул вычисления площади треугольника.
Первая теорема
Площадь треугольника равна половине произведения его высоты на сторону, к которой она проведена.
Задача №1
Сторона треугольника равна 16, а высота, проведённая к этой стороне, равна 19. Найдите площадь этого треугольника
Решение
Задача №2
У треугольника со сторонами 2 и 10 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 5. Чему равна высота, проведённая ко второй стороне?
Решение
Площадь треугольника равна половине произведения его высоты на сторону, к которой она проведена. Поэтому площадь треугольника в каждом случае будет одинаковой.
Задача №3
На стороне AC треугольника ABC отмечена точка D так, что AD=6, DC=10. Площадь треугольника ABC равна 48. Найдите площадь треугольника BCD.
Решение
Если на стороне треугольника взята точка, которая делит эту сторону в отношении m:n, то отрезок, соединяющий эту точку с вершиной противолежащего угла, делит треугольник на два треугольника, площади которых относятся как m:n:
Отрезок AD относиться к отрезку DC как 6:10. Значить площадь треугольника ABD составляет 6 частей от площади треугольника АВС, а площадь треугольника DBC – 10 частей. Вся площадь треугольника ABC равна 16 частей. По условию площадь треугольника АВС равна 48. Значит площадь треугольника ВСD=(48/16)*10=30.
Ответ 30
Задача №4
Два катета прямоугольного треугольника равны 4 и 10. Найдите площадь этого треугольника.
Решение
Вторая теорема
Площадь прямоугольного треугольника равна половине произведения его катетов.
Ответ 20
Задача №5
В прямоугольном треугольнике один из катетов равен 4, а угол, лежащий напротив него равен 45°. Найдите площадь треугольника
Решение:
Если в прямоугольном треугольнике, один из острых углов равен 45 градусам, то и второй острый угол равен 45 градусам, так как сумма острых углов в прямоугольном треугольнике равна 90 градусов. Если в треугольнике два угла равны, то этот треугольник равнобедренный.
Значит в треугольнике катеты равны 4 ( a=b=4). Найдем площадь равнобедренного прямоугольного треугольника:
Ответ 8
Задача №6
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 8 и 17.
Решение
Вспомним что такое катет и гипотенуза.
Стороны прямоугольного треугольника, которые образуют прямой угол, называются катеты, а третья сторона – гипотенуза.
Чтобы вычислить площадь прямоугольного треугольника, необходимо вычислить второй катет. Для этого воспользуемся теоремой Пифагора.
Теорема Пифагора
Квадрат гипотенузы равен сумме квадратов катетов.
Зная оба катета прямоугольного треугольника, вычислим его площадь:
Ответ 60
Задача №7
Катеты прямоугольного треугольника равны 21 и 72. Найдите высоту, проведенную к гипотенузе.
Решение
В этой задаче, чтобы найти высоту, проведенную к гипотенузе, необходимо воспользоваться двумя формулами нахождения площади треугольника. Первая формула (для прямоугольного треугольника): половина произведения его катетов. Вторая формула: половина произведения высоты на сторону, к которой эта высота проведена. Площадь, вычисленная разными формулами одной фигуры, одинаковая. Для решения, нам понадобятся размеры гипотенузы. Вычислим ее:
Теперь найдем, чему будет равна высота:
Ответ 20,16
Задача №8
Боковая сторона равнобедренного треугольника равна 25, а основание равно 48. Найдите площадь этого треугольника.
Решение.
В этой задаче, площадь треугольника найдем по формуле Герона. Для этого нужно знать полупериметр (периметр, деленный на 2) треугольника и длину каждой стороны.
В равнобедренном треугольнике, боковые стороны равны. Найдем периметр треугольника. Периметр треугольника – это сумма всех длин сторон треугольника
Ответ 168
Задача №9
В прямоугольном треугольнике гипотенуза равна 82, а один из острых углов равен 45°. Найдите площадь треугольника.
Решение
Если в прямоугольном треугольнике, один из острых углов равен 45 градусам, то и второй острый угол равен 45 градусам, так как сумма острых углов в прямоугольном треугольнике равна 90 градусов. Если в треугольнике два угла равны, то этот треугольник равнобедренный.
В нашем случает получается треугольник прямоугольный и равнобедренный т.е. катеты треугольника равны. Найдем катеты прямоугольного треугольника через теорему Пифагора.
Пусть катеты прямоугольного треугольника это Х
Ответ 1681
Задача №10
Решение
Третья теорема. Теорема о площади треугольника (9 класс)
Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
Ответ 50
Спасибо, что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог
Площадь треугольника

Задача
1. В
треугольнике одна из сторон равна 27, а опущенная на нее высота – 11. Найдите
площадь треугольника.
Решение: Площадь треугольника = ½
основания*высоту
Пл.треугольника
= ½*27*11=148,5
Ответ:
148,5
Задача
2. Два
катета прямоугольного треугольника равны 4 и 9. Найдите площадь этого
треугольника.
Решение:
Пл.прямоугольного
треуг. = половине произведения катетов.
Пл.прямоуг.треуг.=(4*9):2=36:2=18
Ответ: 18
Задача
3. Периметр
равнобедренного треугольника равен 144, а основание – 64. Найдите площадь
треугольника.
Решение:
1) Т.к.
Треугольник равнобедренный, из этого следует, что две стороны равны АС=СВ,
найдем длину этих  сторон:
сторон:
АС=СВ=(144-64):2=40.
2)
Формула Герона:
Найдем
полупериметр, т.к. периметр = 144, то полупериметр = 144:2=72.
![]()
Ответ: 768
Задача
4. Найдите
площадь треугольника.

Решение: Для формулы нам необходимо
знать основание и высоту
![]() Основание=32+11=43.
Основание=32+11=43.
Высота
= 60.
S треуг.= ½*60*43=1290
Ответ: 1290
![]()
32+11=43
Задача
5.

 |

6
3
Решение:
Задачу
можно решить по формуле Пика, можно по формуле площади треугольника.
Считаем
по клеточкам основание =3, высота = 6.
S=1/2*3*6= 9
Ответ: 9
Задачи
для самостоятельного решения:
1)
В
треугольнике одна из сторон равна 14, а опущенная на нее высота – 31. Найдите
площадь треугольника.
2)
Сторона
треугольника равна 16, а высота, проведённая к этой стороне, равна 19. Найдите
площадь этого треугольника.
3)
Два катета прямоугольного треугольника равны 7 и 12. Найдите площадь этого
треугольника.
4) Два катета
прямоугольного треугольника равны 18 и 7. Найдите площадь этого треугольника.
5) Периметр
равнобедренного треугольника равен 162, а основание – 72. Найдите площадь
треугольника.
6) Найдите площадь
треугольника

7) Найдите площадь
треугольника

8) Найдите площадь треугольника:

9) Найдите площадь треугольника

10) 
11) 
12) 
13)
14) 15)
15) 
16)
Проверить решение можно по ссылке:
https://onlinetestpad.com/hnl6ukjjcnpgo
3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи на нахождение площади и периметра треугольника
(blacktriangleright) Площадь треугольника равна полупроизведению основания (a) и высоты (h), проведенной к этому основанию.
(blacktriangleright) Формула Герона для площади треугольника:
(large{S_{triangle}=sqrt{p(p-a)(p-b)(p-c)}}), где (p) – полупериметр.
(blacktriangleright) Если треугольники имеют равные высоты ((triangle) и (triangle_{1})), то их площади относятся как основания, к которым эти высоты проведены.
Как следствие: медиана треугольника делит его на два равновеликих (равных по площади) треугольника.
(blacktriangleright) Если треугольники имеют по равному углу ((triangle) и (triangle_{2})), то их площади относятся как произведения сторон, образующих этот угол.
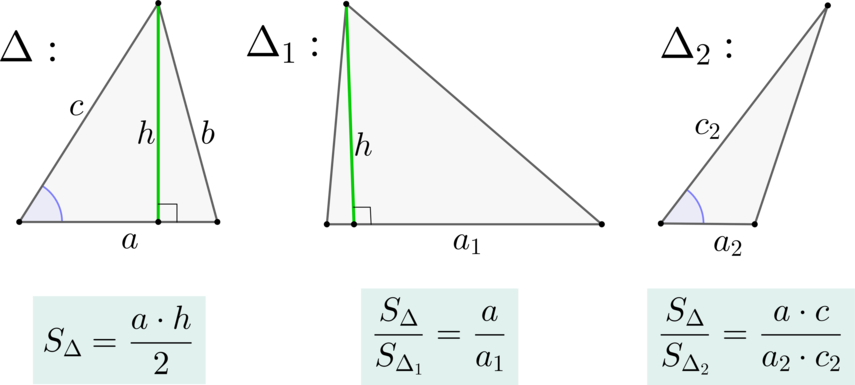
Задание
1
#263
Уровень задания: Равен ЕГЭ
В треугольнике (ABC): (angle C = 90^{circ}), (CM) – медиана, (AC = 4), (CM = 2,5). Найдите периметр треугольника (ABC).
В прямоугольном треугольнике медиана, проведённая к гипотенузе, равна половине гипотенузы, тогда (AB = 2,5 cdot 2 = 5). По теореме Пифагора: (AB^2 = AC^2 + CB^2), откуда находим (CB = 3). Периметр треугольника (ABC) равен (3 + 4 + 5 = 12).
Ответ: 12
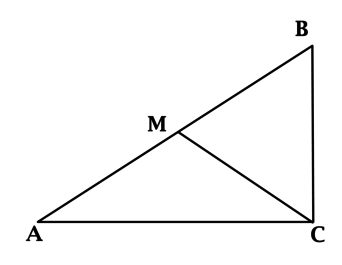
Задание
2
#264
Уровень задания: Равен ЕГЭ
Точка (D) лежит на стороне (AC) треугольника (ABC). Периметр треугольника (ABD) равен (10), периметр треугольника (BDC) равен (7), (BD = 3). Найдите периметр треугольника (ABC).
Периметр треугольника (ABC) равен (AB + AC + BC).
Периметр треугольника (BDC) равен (BD + DC + BC = 7), а (BD = 3), тогда (DC + BC = 4),
периметр треугольника (ABD) равен (AB + BD + AD = 10), тогда (AB + AD = 7).
(AB + AC + BC = AB + AD + DC + BC = 4 + 7 = 11).
Ответ: 11
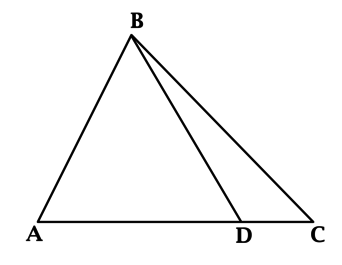
Задание
3
#265
Уровень задания: Равен ЕГЭ
В треугольнике (ABC): (BD) – высота, (AD = 1), (DC = 3), (angle DBC = 45^{circ}). Найдите площадь треугольника (ABC).
(angle BCD = 90^{circ} – angle DBC = 45^{circ} = angle DBC), тогда (BD = DC = 3). Площадь треугольника равна половине произведения основания на высоту, проведённую к этому основанию, тогда площадь треугольника (ABC) равна (0,5 cdot (3 + 1) cdot 3 = 6).
Ответ: 6
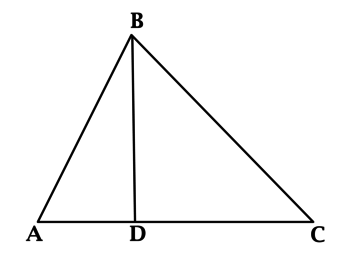
Задание
4
#266
Уровень задания: Равен ЕГЭ
В треугольнике (ABC): (AF) и (BD) – высоты, (AF = 4), (BD = 3), (AC = 6). Найдите (BC).
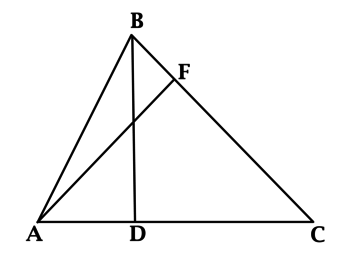
Площадь треугольника равна половине произведения основания на высоту, проведённую к этому основанию. Так как площадь треугольника не зависит от выбора основания, то (0,5 cdot AC cdot BD = 0,5 cdot BC cdot AF), откуда (9 = 0,5 cdot BC cdot 4), значит, (BC = 4,5).
Ответ: 4,5
Задание
5
#2644
Уровень задания: Равен ЕГЭ
Точки (P) и (Q) – середины сторон (AB) и (AC) треугольника (ABC) соответственно. Найдите периметр треугольника (ABC), если периметр треугольника (APQ) равен (21).
(Задача от подписчиков.)
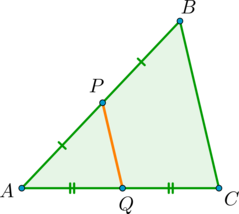
Т.к. (PQ) – средняя линия (triangle ABC), то (2PQ=BC). Периметр (triangle ABC): [P_{ABC}=AB+AC+BC=2AP+2AQ+2PQ=2(AP+AQ+PQ)=2cdot P_{APQ}=2cdot 21=42.]
Ответ: 42
Задание
6
#1768
Уровень задания: Равен ЕГЭ
В треугольнике (ABC): (BD) – медиана. Площадь треугольника (ABD) равна (1). Найдите площадь треугольника (ABC).
Так как медиана делит треугольник на два равновеликих (то есть, с равными площадями), то площадь треугольника (BDC) равна площади треугольника (ABD) и равна (1). Тогда площадь треугольника (ABC), равная сумме площадей треугольников (ABD) и (BDC), равна 2.
Покажем подробнее тот факт, что медиана делит треугольник на два равновеликих треугольника:
площадь треугольника равна половине произведения основания на высоту, проведённую к этому основанию, тогда площадь треугольника (ABD) равна (0,5 cdot AD cdot h), где (h) – высота, проведённая из (B) к стороне (AC). Площадь треугольника (BDC) равна (0,5 cdot
CD cdot h), но (CD = AD), тогда (0,5 cdot AD cdot h = 0,5 cdot
CD cdot h) и, значит, площади треугольников (ABD) и (BDC) равны.
Ответ: 2
Задание
7
#1769
Уровень задания: Равен ЕГЭ
В треугольнике (ABC): точка (D) лежит на (AC), причём (dfrac{AD}{DC} = dfrac{2}{3}). Площадь треугольника (ABD) равна (7,5). Найдите площадь треугольника (BCD).
Построим высоту (BK) 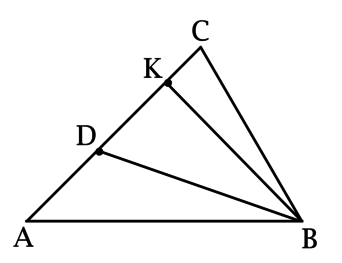
Площадь треугольника (ABD) может быть найдена по формуле: (S_{ABD} = 0,5cdot ADcdot BK).
Аналогично (S_{BCD} = 0,5cdot CDcdot BK), откуда можно сделать вывод:
(dfrac{S_{BCD}}{S_{ABD}} = dfrac{0,5cdot CDcdot BK}{0,5cdot ADcdot BK} = dfrac{CD}{AD} = dfrac{3}{2}), тогда (S_{BCD} = dfrac{3}{2}cdot S_{ABD} = dfrac{3}{2}cdot 7,5 = 11,25).
Ответ: 11,25
Задачи на нахождение площади и периметра равностороннего и равнобедренного треугольника каждый год включаются в программу ЕГЭ по математике. Понимать принцип их решения должны старшеклассники, которые планируют сдавать базовый и профильный уровень аттестационного испытания. Научившись правильно решать задачи на нахождение периметра треугольника в ЕГЭ, школьники смогут оперативно выполнять задания в несколько действий и рассчитывать на получение достаточно высоких баллов по результатам сдачи единого госэкзамена.
Подготовка к аттестационному испытанию вместе со «Школково» — залог вашего успеха
Зачастую во время занятий накануне сдачи единого государственного экзамена перед учащимися встает проблема поиска подходящего источника. Школьного учебника иногда просто не оказывается под рукой в нужный момент. А подобрать все необходимые формулы, к примеру, для вычисления площади прямоугольного треугольника оказывается вовсе не так легко даже в Интернете.
Чтобы успешно пройти выпускное аттестационное испытание, рекомендуем вам заниматься вместе с образовательным порталом «Школково». Наш ресурс предлагает учащимся и преподавателям выстроить процесс подготовки к единому госэкзамену по-новому. Занимаясь вместе с нами, старшеклассники смогут определить те разделы, которые вызывают у них наибольшие трудности, и улучшить собственные знания.
На сайте «Школково» собран весь базовый материал по теме «Вычисление длин и площадей треугольника», который позволит качественно подготовиться к единому государственному экзамену. Данная информация систематизирована и изложена нашими специалистами с учетом их богатого опыта максимально просто и понятно.
Чтобы задачи ЕГЭ на вычисление площади правильного треугольника по трем сторонам не вызывали особых затруднений, мы предлагаем также попрактиковаться в выполнении соответствующих упражнений. Множество подобных заданий представлено в разделе «Каталог». В каждом из них старшеклассники смогут увидеть подробный алгоритм решения и правильный ответ. Базу упражнений в соответствующем разделе мы регулярно обновляем и дополняем.
Выполнять задания на нахождение высоты треугольника или его площади учащиеся из МО и других регионов нашей страны могут в онлайн-режиме. В случае необходимости выполненное упражнение можно сохранить в разделе «Избранное». В дальнейшем задачу, к примеру, на вычисление периметра треугольника можно будет оперативно найти, чтобы обсудить принцип ее решения со школьным преподавателем или репетитором.

УСТАЛ? Просто отдохни
Привет! Это первая статья посвящённая планиметрии.
В ней речь пойдёт о задачах на площадь треугольника.
Вспомним основные формулы для площади треугольника.
Формулы для площади треугольника
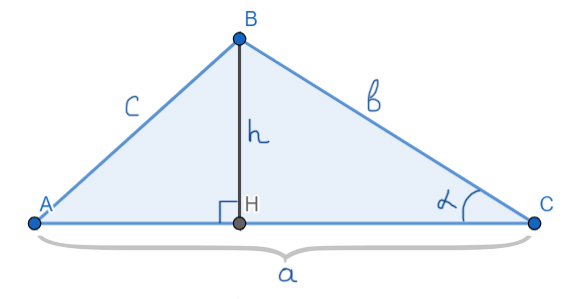
Основная формула:
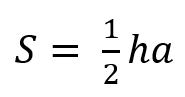
Площадь треугольника равна половине произведения основания на высоту.
Запасная формула:
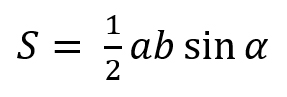
Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
Формула Герона:
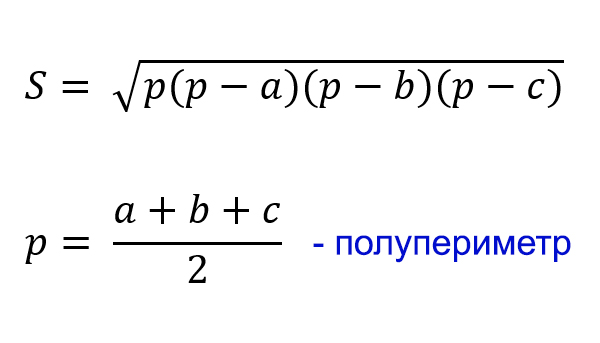
Решение задач
Приступим к тренировочным задачам задания №1 из ЕГЭ по математике профильного уровня на площадь треугольника.
Задача (Прямоугольный треугольник)
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 16 и 20.
Решение:
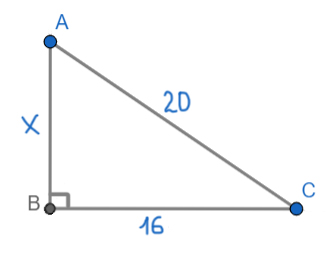
Здесь можно воспользоваться основной формулой для нахождения площади прямоугольного треугольника. Но важно знать, что любой катет — это и есть высота прямоугольного треугольника.
Таким образом, высота будет, к примеру, сторона AB. Тогда основанием будет сторона ВС.
Найдём сторону АВ по теореме Пифагора.
x2 + 162 = 202
x2 = 400 – 256 = 144
x = 12
Тогда площадь будет равна:
S = 0,5 * 12 * 16 = 6 * 16 = 96
Ответ: 96
Задача (Прямоугольный треугольник, закрепление)
Катеты прямоугольного треугольника равны 6 и 8. Найдите высоту, проведённую к гипотенузе.
Решение:
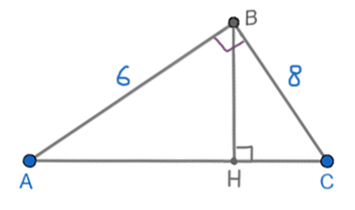
Найдём гипотенузу по теореме Пифагора.
AC2 = AB2 + BC2
AC2 = 62 + 82 = 100
AC = 10
Мы в прошлой задаче выяснили, что площадь прямоугольного треугольника можно найти, как половину произведения его катетов. А с другой стороны, исходя из основной формулы, площадь равна половине произведения высоты ВН и основания (гипотенузы AC).
S = 0,5*AB*BC = 0,5*BH*AC
BH = AB*BC / AC = 6*8 / 10 = 4,8
Ответ: 4,8
Задача (Три треугольника, одна высота)
На стороне AC треугольника ABC отмечена точка D так, что AD=3, DC=7. Площадь треугольника ABC равна 100. Найдите площадь треугольника BCD.
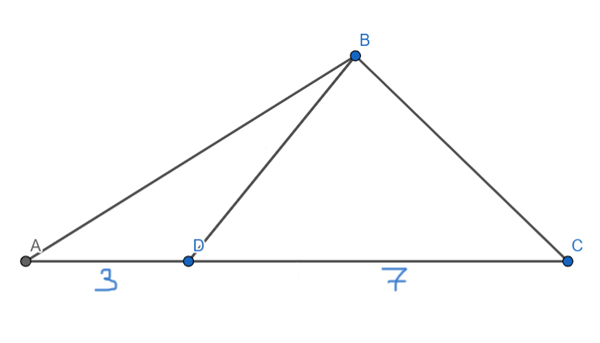
Решение:
Проведём в треугольнике ABC высоту BH. Оказывается, что ВН является высотой и для треугольника ABD, и для треугольника DBC, и для треугольника ABC.
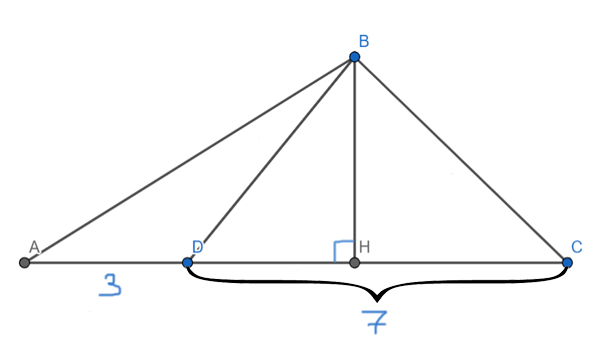
Применим основную формулу для треугольника ABC и найдём высоту BH.
SABC = 0,5 * AC *BH
SABC = 0,5 * 10 * BH = 100
BH = 100 / (0,5*10) = 20
Теперь применим основную формулу, чтобы найти площадь треугольника BCD.
SDBC = 0,5 * DC * BH
SDBC = 0,5 * 7 * 20 = 70
Ответ: 70
Задача (Запасная формула)
В равнобедренном треугольнике ABC (AB = BC) угол при основании равен 15°. Боковая сторона равна 10. Найдите площадь треугольника ABC.
Решение:
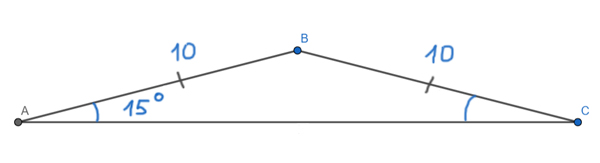
Здесь удобно использовать запасную формулу. Мы знаем две боковые стороны треугольника. Остаётся найти синус угла между ними.
Мы знаем, что углы при основании равны в равнобедренном треугольнике. Поэтому
∠ABC + ∠ВАС + ∠BCA = 180°
∠ABC = 180° – ∠ВАС – ∠BCA
∠ABC = 180° – 15° – 15° = 150°
Синус угла 150° известен. Он равен sin(150°) = sin(30°) = 0,5. Тогда
S = 0,5 * AB*BC * sin(∠ABC)
S = 0,5 * 10*10 * 0,5 = 25
Ответ: 25
Задача (Треугольники в ромбе)
Найдите площадь ромба, если один из его углов равен 60°, а меньшая диагональ равна 10. В ответе запишите число, делённое на √3.
Решение:
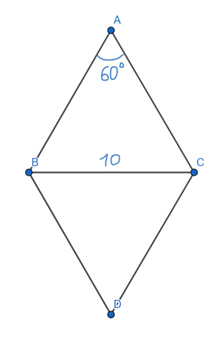
Меньшая диагональ будет находится напротив угла 60°, т.к. второй угол у ромба будет 120°, и напротив этого угла будет находится большая диагональ.
Рассмотрим треугольник ВАС. Мы знаем, что у ромба все стороны равны, поэтому треугольник ВАС равносторонний. Ведь, ВА = АС ⇒ ∠ABC = ∠ACB. Тогда
∠ABC + ∠ACB + ∠BAC = 180°
x = ∠ABC = ∠ACB
x + x + 60° = 180°
2x = 120°
x = 60°
Значит, треугольник ВАС равносторонний. Следовательно, BA = AC = CB = 10.
Чтобы найти площадь ромба, можно разбить его на два одинаковых треугольника: BAC и BDC. Эти два треугольника равны по трём сторонам (BA = AC = CD = DB, BC – общая).
Площадь треугольника BAC легко найти по запасной формуле, ведь две стороны мы знаем, и синус угла между ними тоже известен.
SBAC = 0,5 * BA * AC * sin(60°)
SBAC = 0,5 * 10 * 10 * (√3/2)
SBAC = 25 * √3
Площадь ромба будет равна
SBACD = 2 * SBAC = 2 * 25 * √3 = 50 * √3
В ответе нужно указать число, делённое на √3.
Ответ: 50
Задача (Решаем задачу двумя способами)
На рисунке AB ⊥ BD, AB = 5, AD = 13 и CD = 6. Найдите площадь треугольника CAD.
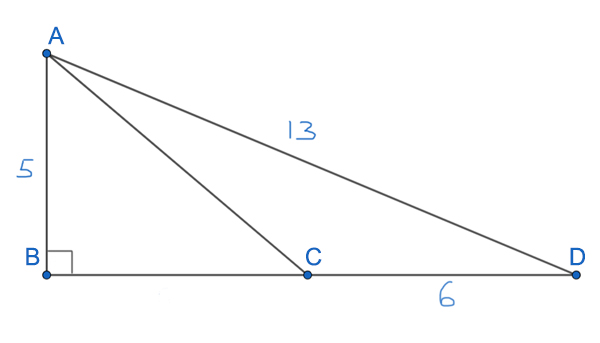
Решение:
Первый способ (основная формула)
Нам известна высота треугольника CAD, AB=5. Нам известно основание, на которое она опущена, это CD=6. Применим основную формулу для площади треугольника.
SCAD = ½ * AB * CD
SCAD = ½ * 5 * 6 = 15
Второй способ (запасная формула)
В прямоугольном треугольнике ABD найдём синус ∠BDA.
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
sin(∠BDA) = AB/AD = 5/13
Теперь воспользуемся запасной формулой для треугольника CAD.
SCAD = ½ * CD * DA * sin(∠BDA)
SCAD = ½ * 6 * 13 * (5/13) = 15
Ответ: 15
Задача (Формула Герона)
Найдите площадь треугольника, стороны которого равны 28, 26, 30.
Решение:
Решим по формуле Герона.
Найдём полупериметр.
p=(28+26+30)/2 = 42
Тогда
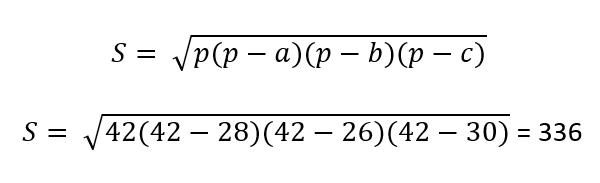
Ответ: 336
На этом всё! Сегодня мы повторили основные формулы для нахождения площади треугольника и порешали задачи на эту темы. Всем удачи!
§2. Площадь треугольника. Метод площадей
В школьном курсе геометрии доказано несколько формул площади треугольника. Напомним их.
Пусть `A`, `B` и `C` – углы треугольника`ABC`; `a`, `b` и `c` – противолежащие этим углам стороны; `h_a`, `h_b` и `h_c` – высоты к этим сторонам; `r` – радиус вписанной окружности;`R` – радиус описанной окружности; `2p=(a+b+c)` – периметр треугольника; `S` – площадь треугольника
| `S=1/2ah_a=1/2bh_b=1/2ch_c`, | (1) |
| `S=1/2 ab sinC=1/2acsinB=1/2bcsinA`, | (2) |
| `S=pr`, | (3) |
| ``S=sqrt(p(p-a)(p-b)(p-c))` – формула Герона, | (4) |
| `S=(abc)/(4R)`. | (5) |
При вычислении площади из этих формул следует выбрать ту, которая в условиях конкретной задачи приводит к более простому решению.
Для примера, рассмотрим два треугольника:
`DeltaABC:` `AB=13`, `BC=14`, `AC=15`;
`DeltaKML:` `KL=sqrt(13)`, `LM=sqrt(14)`, `KM=sqrt(15)`;
Надо найти площадь и радиус описанной окружности.
Для треугольника `ABC` удобен ход решения такой:
`p=1/2(AB+BC+AC)=21`, по формуле Герона
`S_(ABC)=sqrt(21*6*7*8)= ul(84)` и по формуле (5)
`R=(abc)/(4S)=(13*14*15)/(4*84)=65/8=ul(8,125)`.
Для треугольника `KLM` вычисленная по формуле Герона затруднительны, более простой путь – найти косинус, например, угла `M`. По теореме косинусов
`13=14+15-2sqrt(14)*sqrt(15)cosM iffcosM=8/(sqrt(14)*sqrt(15))`,
тогда `sinM=sqrt(1-64/(210))=(sqrt(146))/(sqrt(14)*sqrt(15))` и по формуле (2):
`S_(KML)=1/2KM*LMsinM=1/2*(sqrt(14)*sqrt(15)*sqrt(146))/(sqrt(14)*sqrt(15))=(sqrt(146))/2`,
тогда `R=(KL)/(2sinM)=ul((sqrt(13)*sqrt(14)*sqrt(15))/(2*sqrt(146)))=(sqrt(13)*sqrt7*sqrt(15))/(2*sqrt(73))` (точно также по формуле 5).
Сравнение площадей треугольников обычно опирается на одно из следующих утверждений:
$$ 2.{1}^{○}$$. Площади треугольников с одинаковой высотой относятся как длины соответствующих оснований. В частности, если точка `D` лежит на основании `AC` (рис. 6а), то
`(S_(DBC))/(S_(ABC))=(DC)/(AC)`.
$$ 2.{2}^{○}$$. Площади треугольников с общим углом относятся как произведения сторон, заключающих этот угол (см. рис. 6б):
`(S_(KBL))/(S_(ABC))=(BK*BL)/(BA*BC)`.
$$ 2.{3}^{○}$$. Площади подобных треугольников относятся как квадраты их
сходственных сторон, т. е. если `Delta ABC~DeltaA_1B_1C_1`, то `(S_(A_1B_1C_1))/(S_(ABC))=((A_1B_1)/(AB))^2`.
Все эти утверждения легко доказываются с использованием соответственно формул площади (1) и (2).
Обратим внимание на важное свойство медиан треугольника.
Три медианы треугольника разбивают его на `6` треугольников с общей вершиной и равными площадями.
Известно, что три медианы треугольника пересекаются в одной точке и делятся в отношении `2:1`, считая от вершины. Пусть `O` – точка пересечения медиан треугольника `DeltaABC` площади `S` (рис. 7а). Надо доказать, что площади всех шести треугольников с верш иной в точке `O`, составляющих треугольник `ABC`, равны между собой, т. е. равны `1/6S`.
Докажем, например, для треугольника `BOM`, что `S_(BOM)=1/6S_(ABC)`.
Точка `M` – середина стороны `BC` (рис. 7б), по утверждению $$ 2.{1}^{○}$$ о сравнении площадей `S_(ABM)=1/2S`. Медиана `BN`, пересекая медиану `AM` в точке `O` (рис. 7в), делит её в отношении `AO:OM=2:1`, т. е. `OM=1/3AM`. По тому же утверждению $$ 2.{1}^{○}$$ площадь треугольника `BOM` составляет `1//3` площади треугольника `ABM`, т. е.
`S_(BOM)=1/3(1/2S)=1/6S`.
Дан треугольник `ABC`. Точка `D` лежит на стороне `AB`, `AD:DB=1:2`, точка `K` лежит на стороне `BC`, `BK:KC=3:2` (рис. 8а). Отрезки `AK` и `CD` пересекаются в точке `O`. Найти отношение площади четырёхугольника `DBKO` к площади треугольника `ABC`.
1. Обозначим `S_(ABC)=S`, `S_(DBKO)=sigma` и `S_(ADO)=a`. По утверждению $$ 2.{1}^{○}$$ имеем `S_(ABK)=a+sigma=3/5S` (так как `BK:BC=3:5`). Площадь `a` треугольника `ADO` найдём как часть площади треугольника `ADC`, зная, что `S_(ADC)=1/3S` (так как `AD:AB=1:3`).
2. Через точку `D` проведём прямую `DL“||“AK`. По теореме о пересечении сторон угла параллельными прямыми (`/_ABC`, `DL“||“AK`) имеем `(BL)/(LK)=(BD)/(AD)`, откуда `LK=y`.
По той же теореме (`/_DCB`, `OK“||“DL`) получим `(DO)/(DC)=(LK)/(LC)`, `DO=1/3DC`.
3. Теперь находим `S_(ADO):S_(ADC)=DO:DC`, `a=1/3(1/3S)=1/9S`.
(Можно по теореме Менелая для треугольника `BCD` и секущей `CD:`
`(BK)/(KC)*(CO)/(OD)*(DA)/(AB)=1 iff 3/2*(CO)/(OD)*1/3=1 iff CO=2OD=>OD=1/3DC`).
Находим площадь: `sigma=3/5S-a=(3/5-1/9)S=22/45S`.
`22/45`.
Найти площадь треугольника, две стороны которого равны `3` и `7`, а медиана к третьей стороне равна `4` (рис. 9).
Пусть `AB=3`, `BC=7`, `AM=MC` и `BM=4`. Достроим треугольник `ABC` до параллелограмма, для этого на прямой `BM` отложим отрезок `MD=BM` и соединим точки: `A` с `D` и `C` с `D`. Противоположные стороны параллелограмма равны: `(DC=AB)` и равны площади треугольников `ABC` и `DBC` (общее основание `BC` и равные высоты из вершин `A` и `D`).
В треугольнике `DBC` известны все три стороны: `BC=7`, `DC=3`, `BD=2BM=8`.
Находим его площадь по формуле Герона: `p=9`, `S_(BCD)=6sqrt3`.
Значит и `S_(ABC)=6sqrt3`.
В решении этой задачи дополнительным построением получен треугольник, площадь которого равна площади заданного и легко вычисляется по данным задачи. Приведём ещё одну задачу, где сначала вычисляется площадь дополнительно построенной фигуры, а затем легко находится искомая площадь.
Найти площадь треугольника, если его медианы равны `3`, `4` и `5`.
Пусть `O` – точка пересечения медиан треугольника `ABC` (рис. 10) и пусть `m_a=AM=3`, `m_b=BN=4` и `m_c=CP=5`.
По свойству медиан `AO=2/3m_a`, `CO=2/3m_c` и `ON=1/3m_b`. В треугольнике `AOC` известны две стороны `AO` и `CO` и медиана третьей стороны `ON`. Площадь этого треугольника найдём как в предыдущей задаче.
Достроим треугольник `AOC` до параллелограмма `AOCD`, `S_(AOC)=S_(DOC)`, в треугольнике `DOC` известны три стороны:
`DO=2ON=2/3m_b`, `OC=2/3m_c`, `DC=AO=2/3m_a`.
Площадь треугольника `DOC` вычисляем по формуле Герона `S_1=S_(AOC)=S_(DOC)=8/3`. Сравним теперь площадь треугольника `ABC` (обозначим её `S`) с площадью треугольника `AOC`. Из теоремы 2 о медианах и площадях следует `S_(AOC)=S_(AON)+S_(NOC)=2*1/6S=1/3S`.
Итак, `S=3`, `S_1=8`.
В следующей задаче докажем лемму об отношении площади треугольника к площади другого треугольника, построенного из медиан первого.
Найти отношение площади `S` треугольника к площади `S_0` треугольника, составленного из медиан первого.
Рассмотрим рис. 10. В построенном треугольнике `OCD` стороны таковы: `OC=2/3m_c`, `OD=2/3m_b`, `CD=2/3m_a`. Очевидно, что треугольник со сторонами `m_a`, `m_b`, `m_c` подобен (по третьему признаку) треугольнику со сторонами `2/3m_a`, `2/3m_b`, `2/3m_c`.
Из решения предыдущей задачи следует, что `S_(OCD)=S_1=1/3S` (здесь `S` – площадь треугольника `ABC`). Кроме того, площади подобных треугольников относятся как квадраты сходственных сторон, поэтому `(S_1)/(S_0)=(2/3)^2`. Таким образом, имеем `S_0=9/4S_1=3/4S`, т. е.
`S_(m_am_bm_c)=3/4S_(abc)`.
Из рассуждений в решении Примера 9 следует, что всегда существует треугольник со сторонами, равными медианам данного треугольника, поскольку всегда существует подобный ему треугольник со сторонами `2/3m_a`, `2/3m_b`, `2/3m_c`. Кроме того, становится ясным план построения треугольника по трём отрезкам, равным его медианам: сначала строится треугольник `OCD` (см. рис. 10) со сторонами `2/3m_a`, `2/3m_b`, `2/3m_c`, затем точка `N` – середина отрезка `OD`, потом точка `A` (из `AN=NC`) и точка `B` (из `OB=OD`). Это построение осуществимо, если существует треугольник `OCD`, т. е. если существует треугольник со сторонами `m_a`, `m_b`, `m_c`. Итак, вывод: три отрезка могут быть медианами некоторого треугольника тогда и только тогда, когда из них можно составить треугольник.
Около окружности радиуса `sqrt3` описан треугольник. Найти его площадь, если одна из его сторон точкой касания делится на отрезки `9` и `5`.
Пусть `AP=9`, `PC=5` (рис. 11) и пусть `BM=x`. По свойству касательных `AM=AP`, `CN=CP` и `BN=BM`, поэтому стороны треугольника таковы: `AC=14`, `AB=9+x`, `BC=5+x`, тогда `p=14+x`. (Заметим, что `p=AC+BM`!). По формулам площади (3) и (4) имеем: `S=pr=(14+x)sqrt3` и `S=sqrt((14+x)x*5*9)`. Приравниваем правые части, возводим в квадрат, приводим подобные члены, получаем `x=1`. Вычисляем площадь треугольника:
`S=pr=(14+1)*sqrt3=15sqrt3`.
Приём, применённый в решении этой задачи, когда площадь фигуры выражается двумя различными способами, часто используется в задачах на доказательство.
Проведём два примера, в каждом выведем полезную формулу.
В треугольнике `ABC` угол `C` равен `varphi`, `AC=b`, `BC=a` (рис. 12). Доказать, что биссектриса `CD` равна `(2ab)/(a+b) cos varphi/2`.
Обозначим `CD=x`. Очевидно, что `S_(ABC)=S_(ACD)+S_(DCB)`. По формуле (2) `S_(ABC)=1/2 ab sin varphi`, `S_(ACD)=1/2 bx sin varphi/2`, `S_(BDC)=1/2 ax sin varphi/2`. Таким образом, имеем: `1/2 ab sin varphi=1/2(a+b)x sin varphi/2`. Используем формулу синуса двойного угла `sin varphi=2sin varphi/2 cos varphi/2`, получим:
`x=(2ab)/(a+b)cos varphi/2`.
называется окружность, касающаяся одной из сторон треугольника и продолжений двух других сторон. Таких окружностей, очевидно, три (рис. 13). Их радиусы обычно обозначаются `r_a`, `r_b`, `r_c` в зависимости от того, какой стороны окружность касается.
Вневписанная окружность касается стороны `a=BC` треугольника `ABC` (рис. 14). Доказать, что `S_(ABC)=r_a(p-a)`, где `2p=a+b+c`.
Центр окружности `I_a` лежит на пересечении биссектрисы угла `A` и биссектрис внешних углов при вершинах `B` и `C`. Легко видеть, что если `D`, `F` и `E` – точки касания, то `I_aD=I_aF=I_aE=r_a`.
Считаем площадь `S_0` четырёхугольника `ABI_aC`:
`S_0=S_(ABC)+S_(BCI_a)` и `S_0=S_(ABI_a)+S_(ACI_a)`, откуда
`S_(ABC)=S_(ABI_a)+S_(ACI_a)-S_(BCI_a)=1/2 cr_a+1/2br_a-1/2ar_a=`
`=r_a (c+b-a)/2=r_a(2p-2a)/2=r_a(p-a)`.
Итак,
