ВО 2 классе треугольники рисуют в тетради в клеточку
поэтому
1. сначала считаешь сколько целых клеточек помещается в треугольнике
2. потом считаешь сколько нецелых клеточек помещается в треугольнике и делишь на 2
3. суммируешь
************************
таким же образом считаешь площадь любой фигуры )))
удачи !
************************
можно конечно и следующим образом (он является разновидностью первого)
1. сначала считаешь сколько целых клеточек помещается в треугольнике
2. потом считаешь сколько клеточек помещается в треугольнике в том числе и те клетки, часть которых попала в треугольник
3. суммируешь, делишь на 2
****************************
замечание к ответу удачника
– мой ребенок ходит в школу, сейчас в 3 классе, таблицу умножения прошли частично
как он умножит основание 9 на высоту 12, если он этого еще не умеет делать
а квадратики он считать умеет и делить на 2 умеет
– возьмем треугольник у которого нет ни горизонтальных ни вертикальных сторон
как узнать высоту и сторону треугольника ученику 2 класса
Как найти площадь треугольника
О чем эта статья:
8 класс, 9 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
Площадь — это численная характеристика, которая дает нам информацию о размере части плоскости, ограниченной замкнутой геометрической фигурой.
Если значения заданы в разных единицах измерения длины, мы не сможем узнать, какая площадь треугольника получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
Популярные единицы измерения площади:
- квадратный миллиметр (мм 2 );
- квадратный сантиметр (см 2 );
- квадратный дециметр (дм 2 );
- квадратный метр (м 2 );
- квадратный километр (км 2 );
- гектар (га).
Формула площади треугольника
Для решения задач применяются различные формулы, в зависимости от известных исходных данных. Далее мы рассмотрим способы решения для всех типов треугольников, в том числе частные случаи для равносторонних, равнобедренных и прямоугольных фигур.
Быстро вычислить площадь треугольника поможет наш онлайн-калькулятор. Просто введите известные вам значения и получите ответ в метрах, сантиметрах или миллиметрах.
Научиться быстро щелкать задачки на нахождение площади треугольника помогут курсы по математике от Skysmart!
Общая формула
1. Площадь треугольника через основание и высоту
, где — основание, — высота.
2. Площадь треугольника через две стороны и угол между ними
, где , — стороны, — угол между ними.
3. Площадь треугольника через описанную окружность и стороны
, где , , — стороны, — радиус описанной окружности.
4. Площадь треугольника через вписанную окружность и стороны
, где , , — стороны, — радиус вписанной окружности.
Если учитывать, что — это способ поиска полупериметра, то формулу можно записать следующим образом:
5. Площадь треугольника по стороне и двум прилежащим углам
, где — сторона, и — прилежащие углы.
6. Формула Герона для вычисления площади треугольника
Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.
, где , , — стороны, — полупериметр, который можно найти по формуле:
Для прямоугольного треугольника
Площадь треугольника с углом 90° по двум сторонам
Площадь треугольника по гипотенузе и острому углу
, где — гипотенуза, — любой из прилегающих острых углов.
Гипотенузой принято называть сторону, которая лежит напротив прямого угла.
Площадь прямоугольного треугольника по катету и прилежащему углу
, где — катет, — прилежащий угол.
Катетом принято называть одну из двух сторон, образующих прямой угол.
Площадь треугольника через гипотенузу и радиус вписанной окружности
, где — гипотенуза, — радиус вписанной окружности.
Площадь треугольника по отрезкам, на которые делит вписанная окружность его гипотенузу
, где , — части гипотенузы.
Площадь прямоугольного треугольника по формуле Герона
, где , — катеты, — полупериметр, который можно найти по формуле:
Для равнобедренного треугольника
Вычисление площади через основание и высоту
, где — основание, — высота, проведенная к основанию.
Поиск площади через боковые стороны и угол между ними
, где — боковая сторона, — угол между боковыми сторонами.
Площадь равностороннего треугольника через радиус описанной окружности
, где — радиус описанной окружности.
Площадь равностороннего треугольника через радиус вписанной окружности
, где — радиус вписанной окружности.
Площадь равностороннего треугольника через сторону
Площадь равностороннего треугольника через высоту
Таблица формул нахождения площади треугольника
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу, использовать как закладку в тетрадке или учебнике и обращаться к ней по необходимости.
Как найти площадь треугольника – все способы от самых простых до самых сложных
Зависит от того, какой треугольник.
Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.
Если треугольник прямоугольный
То есть один из его углов равен 90 градусам.
Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.
Если он равнобедренный
То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.
Если он равносторонний
То есть все три стороны равны. Ваши действия такие:
- Найдите квадрат стороны – умножьте эту сторону на нее же. Если у вас сторона равна 4, умножьте 4 на 4, будет 16.
- Умножьте полученное значение на корень из 3. Это примерно 1,732050807568877293527.
- Поделите все на 4.
Если известна сторона и высота
Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.
Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.
Если известны две стороны и градус угла между ними
Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:
Если известны длины трех сторон
- Найдите периметр. Для этого сложите все три стороны.
- Найдите полупериметр – разделите периметр на два. Запомните значение.
- Отнимите от полупериметра длину первой стороны. Запомните.
- Отнимите от полупериметра длину второй стороны. Тоже запомните.
- Отнимите от полупериметра длину третьей стороны. И ее запомните.
- Умножьте полупериметр на каждое из этих чисел (разницу с первой, второй и третьей стороной).
- Найдите квадратный корень.
Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.
Если известны три стороны и радиус описанной окружности
Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.
Если известны три стороны и радиус вписанной окружности
Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.
Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.
Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.
Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона
Формула Герона для нахождения площади треугольника:
Через основание и высоту
Формула нахождения площади треугольника с помощью половины его основания и высоту:
Через две стороны и угол
Формула нахождения площади треугольника через две стороны и угол между ними:
Через сторону и два прилежащих угла
Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
Площадь прямоугольного треугольника
Прямоугольный треугольник – треугольник у которого один из углов прямой, т.е. равен 90°.
Формула нахождения площади прямоугольного треугольника через катеты:
Площадь равнобедренного треугольника через стороны
Равнобедренный треугольник – треугольник, в котором две стороны равны. А значит, равны и два угла.
Формула нахождения площади равнобедренного треугольника через две стороны:
Площадь равнобедренного треугольника через основание и угол
Формула нахождения площади равнобедренного треугольника через основание и угол:
Площадь равностороннего треугольника через стороны
Равносторонний треугольник – треугольник, в котором все стороны равны, а каждый угол равен 60°.
Формула нахождения площади равностороннего треугольника через сторону:
Площадь равностороннего треугольника через высоту
Формула нахождения площади равностороннего треугольника через высоту:
Площадь равностороннего треугольника через радиус вписанной окружности
Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
Площадь равностороннего треугольника через радиус описанной окружности
Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
Площадь треугольника через радиус описанной окружности и три стороны
Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
Площадь треугольника через радиус вписанной окружности и три стороны
Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
[spoiler title=”источники:”]
http://vsvoemdome.ru/obrazovanie/kak-nayti-ploschad-treugolnika
http://www.mozgan.ru/Geometry/AreaTriangle
[/spoiler]
Содержание
- – Как найти площадь треугольника по синусу и двум сторонам?
- – Как найти угол если известны 2 стороны?
Как найти площадь треугольника по синусу и двум сторонам?
по двум сторонам и углу между ними: площадь треугольника равна половине произведения его сторон на синус угла между ними; 1.3.
Как найти угол если известны 2 стороны?
Если известны 2 катета – то необходимо воспользоваться арктангенсом (или арккотангенсом). Вычисляем арктангенс из результата деления противолежащего катета на прилежащий – tg−1 (b/a), либо арккотангенс из результата деления прилежащего катета на противолежащий – ctg−1 (a/b).
Интересные материалы:
Какой цвет дает хром?
Какой цвет дивана под серые обои?
Какой цвет дивана подходит под серые обои?
Какой цвет дивана подойдет к бирюзовым обоям?
Какой цвет дивана подойдет к оливковым обоям?
Какой цвет дивана подойдет к серым обоям?
Какой цвет дивана подойдет к желтым обоям?
Какой цвет дивана сейчас в моде?
Какой цвет дивана универсальный?
Какой цвет дивана в моде?
У геометрической фигуры — треугольника — 3 стороны и 3 вершины. Треугольник получается, если три точки, которые не лежат на одной прямой, соединить отрезками.
Для названия треугольника используются большие латинские буквы, при этом соблюдается последовательность вершин, но начинать название можно с любой вершины.
Иногда используют знак Δ.
В зависимости от величин углов треугольника выделяют:
- остроугольные треугольники (все углы острые, как на рисунке выше);
- прямоугольные треугольники (один угол прямой — ∡P=90°);
- тупоугольные треугольники (один угол тупой — ∡M).
Площадь треугольника
Прямоугольный треугольник легко представить как половину прямоугольника.
Если площадь прямоугольника равна произведению длин сторон, то для определения площади треугольника необходимо это произведение разделить на 2.
Допустим, RP = a, TP = b;
SRPT=(ab)/2.
Если треугольник не имеет прямого угла, можно построить два прямоугольника, как показано на рисунке.
Допустим, MA=BD=NC = h, AC = a.
SABC=SABD+SCBD=h⋅AD/2+h⋅DC/2=h⋅AC/2=h⋅a/2.
Как видно, достаточно в треугольнике от одной вершины провести отрезок под прямым углом к противолежащей стороне и использовать длины отрезка для определения площади треугольника.
Отрезок называют высотой треугольника.
Свойства треугольника
- длина любой стороны треугольника меньше суммы длин двух остальных сторон, но больше разницы длин двух остальных сторон;
- высота треугольника образует прямой угол со стороной, к которой проведена;
- площадь треугольника равна половине произведения длины высоты треугольника и длины стороны, к которой проведена высота SABC=a⋅h/2.
Пример. Можно ли построить треугольник из отрезков с длинами: 3 см, 7 см, 4 см?
Пример. Можно ли построить треугольник из отрезков с длинами: 16 см, 32 см, 18 см?
Пример. Можно ли построить треугольник из отрезков с длинами: 1 см, 3 см, 7 см ?
Одна сторона, которая образует прямой угол прямоугольного треугольника ABD, равна 12 см, другая сторона, которая образует прямой угол, в 3 раза меньше.
Определи площадь треугольника.
Рассчитай площадь треугольника ABC, если дана площадь клетки — 1 м2.
Известно, что периметр равностороннего треугольника — 21 см. Определи периметр данного четырёхугольника, который состоит из равносторонних треугольников.
Дан равносторонний треугольник. 2 раза сделано следующее:
1. на всех сторонах отмечены и соединены серединные точки.
2. На сторонах внутреннего треугольника опять отмечены и соединены серединные точки.
Треугольник, который образовался на этот раз, закрашен розовым цветом.
1. Сколько маленьких треугольников необходимо для перекрытия данного треугольника?
2. Чему равна площадь большого треугольника, если площадь розового треугольника равна 4 м²?
3. Сколько маленьких треугольников получится, если повторить эти действия (построить такую конструкцию) 4 раза?
4. Сколько маленьких треугольников получится, если повторить эти действия (построить такую конструкцию) 3 раза?
Определи площадь данных фигур, если площадь одной клетки равна 6 см2.
1)
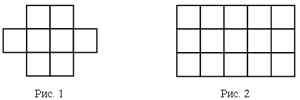
Сколько клеток образует площадь фигуры? Чему равна площадь фигуры?
Сколько клеток образует площадь фигуры? Чему равна площадь фигуры?
Подумай, как построены данные фигуры, и определи, сколько клеток будет у следующих двух фигур, если их построить по той же закономерности.
Цель: познакомиться с понятием площадь
фигуры.
Оборудование: презентация, модели:
квадратные сантиметры, квадратные дециметры,
квадратные метры.
| Этапы урока | Деятельность учителя | Деятельность учащихся |
| I. Мотивирование к учебной деятельности. 1. Организационный момент. |
Здравствуй, мой любимый класс, Очень рада видеть вас! Ты готов начать урок? Всё ль на месте? Всё ль в порядке? Ручки, книжки и тетрадки? |
Приветствуют учителя.
Проверяют свою |
| II. Актуализация знаний.
Устный |
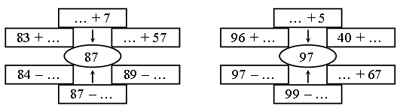
1)Вставьте пропущенные числа.
2) Решите задачу. В аллее 28 каштанов, а ясеней в 4 раза меньше. |
Повторяют правила нахождения неизвестных компонентов сложения и вычитания, закрепляют таблицу умножения. |
| III. Определение темы урока.
1. 2. Постановка проблемы. |
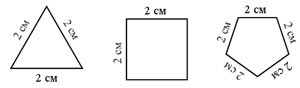
– Как называются данные на доске фигуры? – Что их объединяет? (Это многоугольники,
– Как найти периметр каждого многоугольника? 2 + 2 + 2 = 6 (см) 2 + 2 +2 + 2 = 8 (см). 2 + 2 + 2 + 2 + 2 = 10 (см). – Как найти площадь этих фигур? – Какие трудности у вас возникли? – Сегодня на уроке мы узнаем, что называют |
Фиксируют затруднение. |
| IV. Открытие нового знания. | Какая фигура меньше занимает места на плоскости? Говорят, что треугольник имеет – Площадь какой фигуры больше? Площадь – свойство фигуры, занимать место на Площадь – это внутренняя часть фигуры. – Площадь квадрата больше, чем площадь круга? – Площадь какой фигуры больше красной или – Сможем ли мы сравнить площади фигур – Наложить мы не сможем эти фигуры, но можем Площадь фигуры можно измерять и другими Сравните жёлтый и красный прямоугольники по – Сколько квадратов в первом прямоугольнике, во – Почему так получилось? Чтобы этого не было вводятся специальные |
Работают с презентацией.
Треугольник Площадь четырёхугольника больше, чем площадь Площадь квадрата больше, чем площадь круга. Площадь двух кругов одинаковая. Сравнивают прямоугольники по количеству Т.к. фигуры разбиты на квадраты разных размеров. |
| V. Первичное закрепление.
Работа |
– Образуйте фигуры, площадь которой 3 кв. см.(5,4 кв.см) Назовите площадь. Фигуры у всех -Образуйте фигуры, площадь которой 5 кв. см. (4 Чтение правила по учебнику стр. 27.
(Квадратным сантиметром называют площадь
– Сформулируйте определение квадратного – Квадратный сантиметр, квадратный дециметр, Их обозначают так: см2, дм2, м2. – Рассмотрите вырезанные из бумаги квадраты – Сравните попарно площади этих квадратов. – В квадрате площадью 1 дм2 может |
Работают в парах. У учащихся модели У наших фигур одинаковые площади. Читают определение квадратного дециметра, Сравнивают попарно площади этих квадратов, |
| Физминутка. | Определите площади фигур на экране.
1) Площадь одного такого квадрата называют квадратным 2) Прямоугольник на рисунке состоит из 3 полос, |
1) Фигура состоит из 8 квадратов со стороной 1 см каждый. Значит, площадь всей фигуры равна 8 см2. 2) Весь прямоугольник состоит из 5 * 3 = 15 таких |
| VI. Самостоятель ная работа. Работа в группах. |
Дополни высказывание.
|
Работают в группах. Дополняют высказывание. |
| VIII. Систематизация и повторение. | Задание № 3 (с. 28).
Работа в печатной
Задание № 3,стр.13.
Напиши площадь данных фигур. |
Читают величины, записанные единицами площади. Устанавливают взаимосвязь между Записывают площадь фигур. |
| VII. Итог урока. | Выбери правильное утверждение:
1. 2. Площадь – это … – Назовите единицы измерения площади фигуры. Пригодится ли вам в жизни умение находить – Где и зачем? |
Выбирают правильное утверждение. |
| Рефлексия деятельности. | Покажите своё настроение в конце урока смайликом. – Что не получилось? Почему? |
Литература.