Как найти площадь треугольника зная длину гипотенузы - Сайт, где вы сможете решить свои вопросы

Найти площадь прямоугольного треугольника

Главная
/
Математика
/
Геометрия
/
Найти площадь прямоугольного треугольника

Чтобы посчитать площадь прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Чтобы вычислить площадь прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):

длины катетов a и b
длину гипотенузы с и длину любого из катетов (a или b)
длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
длину гипотенузы с и один из острых углов (α или β)

Найти площадь прямоугольного треугольника по двум катетам

Катет a =
Катет b =
S =

Просто введите длины двух катетов, и получите ответ.

Теория

Чему равна площадь (S) прямоугольного треугольника если известны оба катета (a и b)?

Формула

S = ½ ⋅ a ⋅ b

Пример

К примеру найдём площадь прямоугольного треугольника у которого сторона a = 2 см, а сторона b = 4 см:

S = 2 ⋅ 4 / 2 = 8 / 2 = 4 см²

Найти площадь прямоугольного треугольника по катету и гипотенузе

Гипотенуза c =
Катет (a или b) =
S =

Введите длины гипотенузы и одного из катетов, и получите ответ.

Теория

Чему равна площадь (S) прямоугольного треугольника если известны его гипотенуза (c) и один из катетов (a или b)?

Формула

S = ½ ⋅ a ⋅ √c² – a² = ½ ⋅ b ⋅ √c² – b²

Пример

К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 2 см, а гипотенуза c = 5 см:

S = 2 ⋅ √5² – 2² / 2 = √25 – 4 ≈ 4.58 см²

Найти площадь прямоугольного треугольника по катету и прилежащему к нему острому углу

Катет (a или b) =
Прилежащий угол (β или α) = °
S =

Введите длину одного из катетов и прилежащий к нему острый угол в градусах.

То есть к катету a прилежащий ∠β, а к катету b – ∠α

Теория

Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и прилежащий к нему угол?

Формула

S = ½ ⋅ a² ⋅ tg(β) = ½ ⋅ b² ⋅ tg(α)

Пример

К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а прилежащий к нему ∠β = 45°:

S = ½ ⋅ 4² ⋅ tg(45) = ½ ⋅ 16 ⋅ 1 = 16 / 2 = 8 см²

Найти площадь прямоугольного треугольника по катету и противолежащему к нему острому углу

Катет (a или b) =
Противолежащий угол (α или β) = °
S =

Введите длину одного из катетов и противолежащий к нему острый угол в градусах.

То есть к катету a противолежащий ∠α, а к катету b – ∠β

Теория

Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и противолежащий к нему угол?

Формула

S = ½ ⋅ a² ⋅ tg(90 – α) = ½ ⋅ b² ⋅ tg(90 – β)

Пример

К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а противолежащий к нему ∠α = 45°:

S = 4² / 2⋅ tg(45) = 16 / 2 ⋅ 1 = 8 см²

Найти площадь прямоугольного треугольника зная длину гипотенузы и один из острых углов

Гипотенуза c =
Угол (α или β) = °
S =

Введите длину гипотенузы и один из острых угол в градусах.

Теория

Чему равна площадь (S) прямоугольного треугольника если известны длина гипотенузы (c) и один из острых углов?

Формула

S = ½ ⋅ c² ⋅ sin(α) ⋅ cos(α) = ½ ⋅ c² ⋅ sin(β) ⋅ cos(β)

Пример

К примеру посчитаем чему равна площадь прямоугольного треугольника у которого гипотенуза c = 8 см, а ∠α = 45°:

S = ½ ⋅ 8² ⋅ sin(45) ⋅ cos(45) ≈ ½ ⋅ 64 ⋅ 0.7071067812 ⋅ 0.7071067812 ≈ 16 см²

Источник

Формула:

S
=

1

2

ab

Где: a, b – стороны.

цифр после запятой

обновите расчет!!!

укажите правильное значение!!!

скопировано

Формула:

S
=

1

4

С2
·sin(2α)

Где: C – гипотенуза, α – острый угол.

цифр после запятой

обновите расчет!!!

укажите правильное значение!!!

скопировано

Формула:

S
=

1

2

a2
·tg(α)

Где: a – катет, α – острый угол.

цифр после запятой

обновите расчет!!!

укажите правильное значение!!!

скопировано

Формула:

S
=
R·(R+C)

Где: С – гипотенуза, R – радиус вписанной окружности.

цифр после запятой

обновите расчет!!!

укажите правильное значение!!!

скопировано

Формула:

S
=

D

2

·(

D

2

+ C
)

Где: С – гипотенуза, D – диаметр вписанной окружности.

цифр после запятой

обновите расчет!!!

укажите правильное значение!!!

скопировано

Формула:

S
=

S

π

·(

S

π

+ C
)

Где: С – гипотенуза, S – площадь вписанной окружности.

цифр после запятой

обновите расчет!!!

укажите правильное значение!!!

скопировано

Формула:

S
=

P

2π

·(

P

2π

+ C
)

Где: С – гипотенуза, P – длина вписанной окружности.

цифр после запятой

обновите расчет!!!

укажите правильное значение!!!

скопировано

Формула:

S
=

C1

·

C2

Где: C1 , C2 – части гипотенузы.

цифр после запятой

обновите расчет!!!

укажите правильное значение!!!

скопировано

Формула:

S
=

1

2

ch

Где: c – гипотенуза, h – высота.

цифр после запятой

обновите расчет!!!

укажите правильное значение!!!

скопировано

Площадь треугольника равна одной четверной квадрата гипотенузы умноженной на синус двойного угла.

Калькуляторы площади прямоугольного треугольника

Источник

Найти площадь прямоугольного треугольника

Онлайн калькулятор

Чтобы вычислить площадь прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):

длины катетов a и b
длину гипотенузы с и длину любого из катетов (a или b)
длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
длину гипотенузы с и один из острых углов (α или β)

Найти площадь прямоугольного треугольника по двум катетам

Теория

Чему равна площадь (S) прямоугольного треугольника если известны оба катета (a и b)?

Формула

Пример

К примеру найдём площадь прямоугольного треугольника у которого сторона a = 2 см, а сторона b = 4 см:

S = 2 ⋅ 4 / 2 = 8 / 2 = 4 см²

Найти площадь прямоугольного треугольника по катету и гипотенузе

Теория

Чему равна площадь (S) прямоугольного треугольника если известны его гипотенуза (c) и один из катетов (a или b)?

Формула

S = ½ ⋅ a ⋅ √ c² – a² = ½ ⋅ b ⋅ √ c² – b²

Пример

S = 2 ⋅ √ 5² – 2² / 2 = √ 25 – 4 ≈ 4.58 см²

Найти площадь прямоугольного треугольника по катету и прилежащему к нему острому углу

То есть к катету a прилежащий ∠β, а к катету b – ∠α

Теория

Формула

S = ½ ⋅ a² ⋅ tg(β) = ½ ⋅ b² ⋅ tg(α)

Пример

S = ½ ⋅ 4² ⋅ tg(45) = ½ ⋅ 16 ⋅ 1 = 16 / 2 = 8 см²

Найти площадь прямоугольного треугольника по катету и противолежащему к нему острому углу

То есть к катету a противолежащий ∠α, а к катету b – ∠β

Теория

Формула

S = ½ ⋅ a² ⋅ tg(90 – α) = ½ ⋅ b² ⋅ tg(90 – β)

Пример

S = 4² / 2⋅ tg(45) = 16 / 2 ⋅ 1 = 8 см²

Найти площадь прямоугольного треугольника зная длину гипотенузы и один из острых углов

Теория

Чему равна площадь (S) прямоугольного треугольника если известны длина гипотенузы (c) и один из острых углов?

Формула

S = ½ ⋅ c² ⋅ sin(α) ⋅ cos(α) = ½ ⋅ c² ⋅ sin(β) ⋅ cos(β)

Пример

К примеру посчитаем чему равна площадь прямоугольного треугольника у которого гипотенуза c = 8 см, а ∠α = 45°:

S = ½ ⋅ 8² ⋅ sin(45) ⋅ cos(45) ≈ ½ ⋅ 64 ⋅ 0.7071067812 ⋅ 0.7071067812 ≈ 16 см²

Площадь прямоугольного треугольника

О чем эта статья:

площадь, 8 класс

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Основные определения

Прямоугольный треугольник — это треугольник, в котором один угол прямой, то есть равен 90˚.

Гипотенуза — это сторона, противолежащая прямому углу.

Катеты — это стороны, прилежащие к прямому углу.

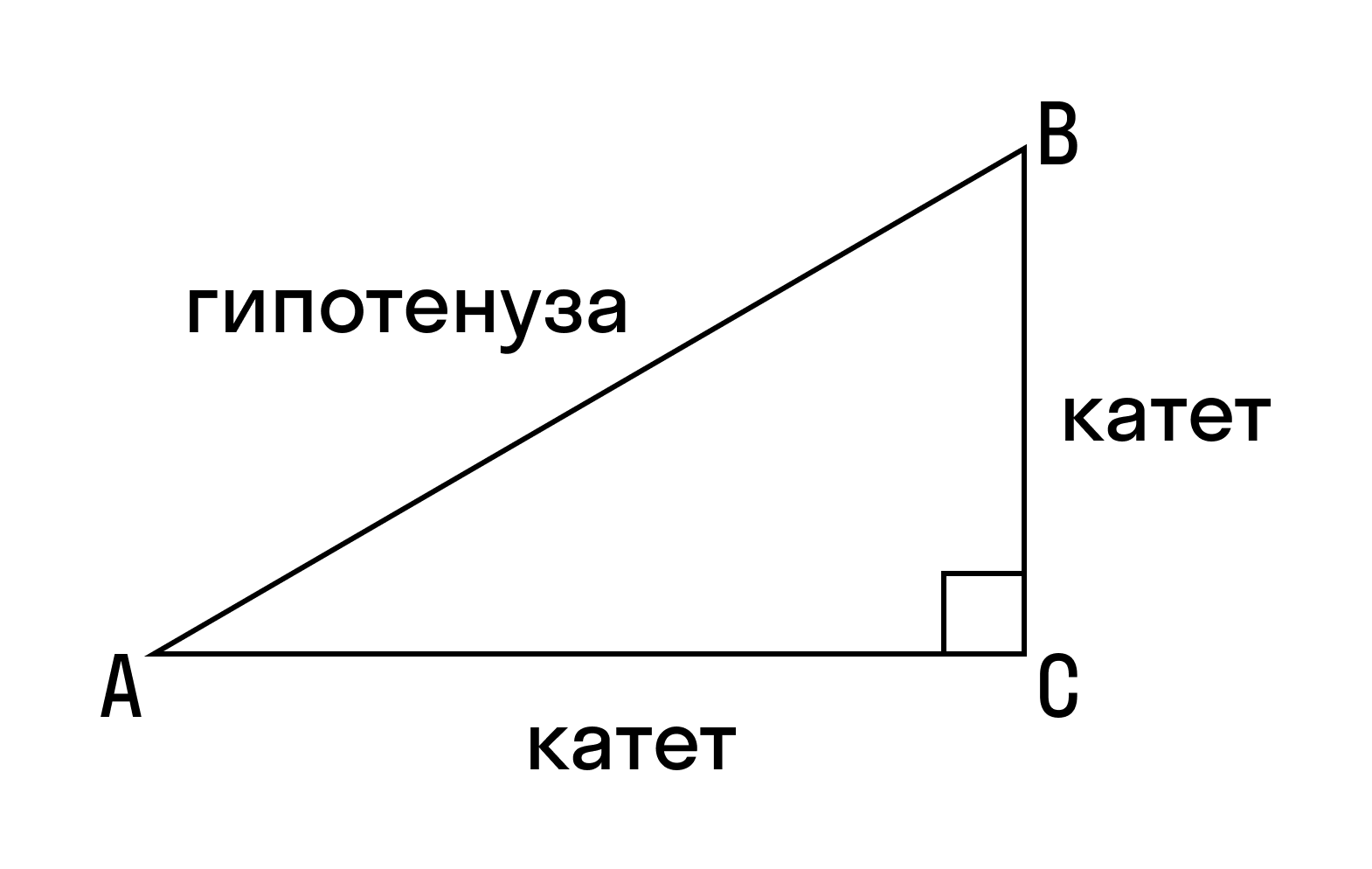
Чтобы найти площадь прямоугольного треугольника, можно применить любую формулу нахождения площади треугольника — их несколько.

Формула для нахождения площади прямоугольного треугольника через катеты

Чтобы найти площадь, нужно вывести формулу:

Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию.

Так как в прямоугольном треугольнике катеты перпендикулярны, то один катет — это высота, проведенная ко второму катету.

Отсюда следует, что площадь прямоугольного треугольника равна половине произведения его катетов.

Используйте эту формулу, чтобы найти площадь прямоугольного треугольника через катеты.

S = 1/2 (a × b), где a и b — катеты

Формула для нахождения площади прямоугольного треугольника через гипотенузу

Площадь прямоугольного треугольника равна половине произведения гипотенузы на высоту, проведенную к гипотенузе.

где с — гипотенуза,

Используйте эту формулу, чтобы найти площадь прямоугольного треугольника через гипотенузу.

Формула для нахождения площади прямоугольного треугольника через гипотенузу и острый угол

α, β — острые углы

Формулы нахождения площади прямоугольного треугольника через катет и угол

α, β — острые углы

Формулы нахождения площади прямоугольного треугольника через радиус вписанной окружности и гипотенузу

Радиус вписанной окружности выражается через катеты и гипотенузу по формуле:

S прямоугольного треугольника = r (r + c) = c1 × c2

r — радиус вписанной окружности

C1 и С2 — отрезки, полученные делением гипотенузы на две части точкой касания с окружностью

Уверены, что во всем разобрались? Закрепите знания на курсах обучения математике в онлайн-школе Skysmart!

Площадь прямоугольного треугольника

Онлайн калькулятор – площадь прямоугольного треугольника

Треугольник – это геометрическая фигура, образованная тремя отрезками соединяющихся тремя точками, у которой все углы внутренние.

Треугольники бывают прямоугольный, равнобедренный, равносторонний.

Катет – это прилежащая прямому углу сторона треугольника.

Гипотенуза – это сторона треугольника противолежащая прямому углу.

Формула площади прямоугольного треугольника

Чтобы посчитать площадь прямоугольного треугольника, необходимо знать размеры двух сторон треугольника.

Площадь прямоугольного треугольника расчитывается по формуле:

S – площадь треугольника
a – катет
b – катет
c – гипотенуза

Если известены размеры только одного катета и гипотенузы, тогда площадь прямоугольного треугольника можно расчитать по формулам:

[spoiler title=”источники:”]

http://skysmart.ru/articles/mathematic/kak-najti-ploshad-pryamougolnogo-treugolnika

http://kalk.top/s/triangle-pr

[/spoiler]

Источник

Площадь прямоугольного треугольника онлайн

С помощю этого онлайн калькулятора можно найти площадь прямоугольного треугольника. Для нахождения площади прямоугольного треугольника введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть и численные примеры смотрите ниже.

Содержание

Площадь прямоугольного треугольника по двум катетам
Площадь прямоугольного треугольника по катету и гипотенузе
Площадь прямоугольного треугольника по гипотенузе и углу
Площадь прямоугольного треугольника по катету и прилежащему углу
Площадь прямоугольного треугольника по катету и противолежащему углу
Площадь прямоугольного треугольника по гипотенузе и вписанной окружности
Площадь прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность

Площадь прямоугольного треугольника по двум катетам

Как известно, площадь треугольника равна половине произведения его основания на высоту (см. страницу Площадь треугольника онлайн).В прямоугольном треугольнике катеты перпендикулярны друг другу. Поэтому можно один из них считать как основание, а другой − как высоту.

На рисунке 1 можем считать a как основание, а b − как высоту. Тогда площадь прямоугольного треугольника равна:

Пример 1. Известны катеты прямоугольного треугольника: 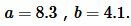Найти площадь треугольника.

Решение. Для вычисления площади треугольника воспользуемся формулой (1). Подставляя значения 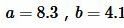в (1), получим:

Ответ:

Площадь прямоугольного треугольника по катету и гипотенузе

Пусть в прямоугольном треугольнике известны катет a и гипотенуза c (Рис.2):

Найдем площадь треугольника. Из формулы Пифагора имеем:

Подставляя (2) в (1), получим формулу вычисления площади прямоугольного треугольника по катету и гипотенузе:

Пример 2. Известны катет и гипотенуза прямоугольного треугольника: 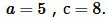Найти площадь треугольника.

Решение. Для вычисления площади треугольника воспользуемся формулой (3). Подставляя значения 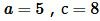в (3), получим:

Ответ: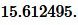

Площадь прямоугольного треугольника по гипотенузе и углу

Пусть в прямоугольном треугольнике известны гипотенуза с и угол α (Рис.3):

Найдем площадь прямоугольного треугольника. Из теоремы синусов имеем:

или

Подставим (4) в (1):

Из формулы произведения тригонометрических функций имеем:

Подставим в (6) ( small beta=alpha ):

Применяя (7) относительно формулы (5), получим:

Пример 3. Известны гипотенуза и прилегающий угол прямоугольного треугольника: 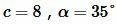. Найти площадь треугольника.

Решение. Для вычисления площади треугольника воспользуемся формулой (8). Подставляя значения 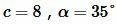в (8), получим:

Ответ: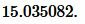

Площадь прямоугольного треугольника по катету и прилежащему углу

Пусть в прямоугольном треугольнике известны катет a и прилежащий угол α (Рис.4):

Найдем площадь прямоугольного треугольника. Тангенс угла α прямоугольного треугольника равна:

Откуда

Подставляя (9) в (1), получим формулу площади прямоугольного треугольника по катету и прилежащему углу:

Пример 4. Известны катет и прилегающий угол прямоугольного треугольника: 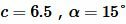. Найти площадь треугольника.

Решение. Для вычисления площади треугольника воспользуемся формулой (10). Подставляя значения 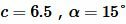в (10), получим:

Ответ:

Площадь прямоугольного треугольника по катету и противолежащему углу

Пусть в прямоугольном треугольнике известны катет a и противолежащий угол α (Рис.5):

Найдем площадь прямоугольного треугольника. Коангенс угла α прямоугольного треугольника равна:

Откуда

Подставляя (12) в (1), получим формулу площади прямоугольного треугольника по катету и противожащему углу:

Пример 5. Известны катет и противолежащий угол прямоугольного треугольника: 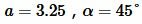. Найти площадь треугольника.

Решение. Для вычисления площади треугольника воспользуемся формулой (13). Подставляя значения 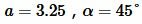в (13), получим:

Ответ: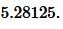

Площадь прямоугольного треугольника по гипотенузе и вписанной окружности

Пусть в прямоугольном треугольнике известны гипотенуза с и радиус вписанной окружности r (Рис.6):

Найдем площадь прямоугольного треугольника. Соединим центр окружности O c вершинами A, B и с точками D, E, F.

Треугольники AOD, AOF, BOD, BOE прямоугольные, поскольку 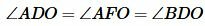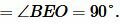Прямоугольные треугольники AOD и AOF равны по гипотенузе и катету (сторона AO общая, OD=OF):

Прямоугольные треугольники BOD и BOE равны по гипотенузе и катету (сторона BO общая, OD=OE):

Запишем формулы площадей прямоугольных треугольников AOD и BOD и квадрата OECF:

Тогда, учитывая (14) и (15), площадь прямоугольного треугольника ABC равна:

Подставляя (16), (17) в (18), получим:

или

Пример 6. Известны гипотенуза и радиус вписанной окружности прямоугольного треугольника: 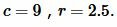Найти площадь треугольника.

Решение. Для вычисления площади треугольника воспользуемся формулой (19). Подставляя значения 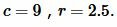в (19), получим:

Ответ: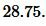

Площадь прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность

Пусть в прямоугольном треугольнике известны отрезки AD и DB (Рис.6). Найдем площадь прямоугольного треугольника выраженные через эти отрезки. Площадь прямоугольного треугольника через катеты имеет вид:

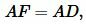
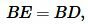
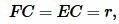
Учитывая, что 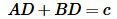, (20) примет вид:

То есть

Сравнивая формулы (19) и (21) можем записать:

Таким образом формула площади прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность имеет следующий вид:

Пример 7. Известны отрезки гипотенузы разделенные вписанной окружностью прямоугольного треугольника (Рис.6) 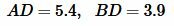Найти площадь треугольника.

Решение. Для вычисления площади треугольника воспользуемся формулой (22). Подставляя значения в (22), получим:

Ответ:

Смотрите также:

Площадь треугольника онлайн
Площадь равностороннего треугольника онлайн
Площадь равнобедренного треугольника онлайн

Источник

{S = dfrac{1}{2} cdot a cdot h}

Задача нахождения площади треугольника довольно распространена не только в науке, но и в быту. Для вас мы разработали калькулятор для нахождения площади любого треугольника – равнобедренного, равностороннего, прямоугольного или обыкновенного (разностороннего) по 22 формулам.

Калькулятор площади треугольника
Площадь треугольника
1. через основание и высоту
2. через две стороны и угол между ними
3. через сторону и два прилежащих угла
4. через радиус описанной окружности и 3 стороны
5. через радиус вписанной окружности и 3 стороны
6. по формуле Герона
Площадь прямоугольного треугольника
1. через катеты
2. через гипотенузу и прилежащий угол
3. через катет и прилежащий угол
4. через радиус вписанной окружности и гипотенузу
5. через вписанную окружность
6. по формуле Герона
7. через катет и гипотенузу
Площадь равнобедренного треугольника
1. через основание и сторону
2. через основание, боковую сторону и угол
3. через основание и высоту
4. через боковые стороны и угол между ними
5. через основание и угол между боковыми сторонами
Площадь равностороннего треугольника
1. через сторону
2. через высоту
3. через радиус описанной окружности
4. через радиус вписанной окружности
Примеры задач

Площадь треугольника

Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.

Площадь треугольника через основание и высоту

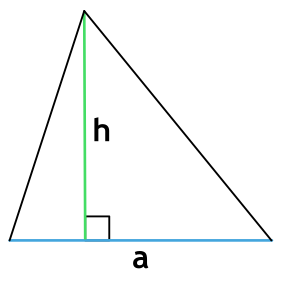
{S = dfrac{1}{2} cdot a cdot h}

a – длина основания

h – высота, проведенная к основанию

Площадь треугольника через две стороны и угол между ними

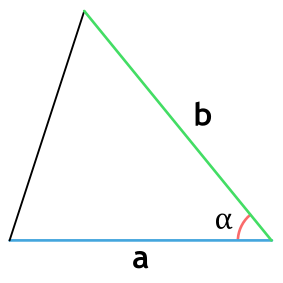
{S = dfrac{1}{2} cdot a cdot b cdot sin(alpha)}

a и b – стороны треугольника

α – угол между сторонами a и b

Площадь треугольника через сторону и два прилежащих угла

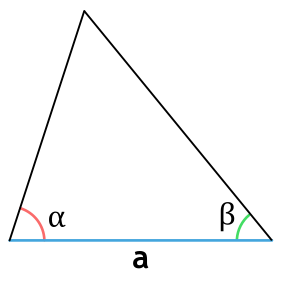
{S = dfrac{a^2}{2} cdot dfrac{sin{(alpha)} cdot sin{(beta)}}{sin{(gamma)}}}
{gamma = 180 – (alpha + beta)}

a – сторона треугольника

α и β – прилежащие к стороне a углы

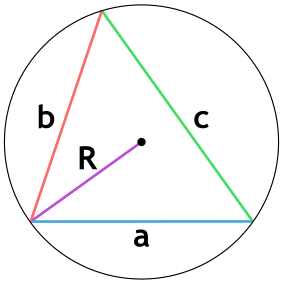
Площадь треугольника через радиус описанной окружности и 3 стороны

{S = dfrac{a cdot b cdot c}{4 cdot R}}

a, b и c – стороны треугольника

R – радиус описанной окружности

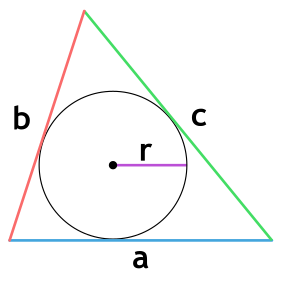
Площадь треугольника через радиус вписанной окружности и 3 стороны

{S = r cdot dfrac{a + b + c}{2}}

a, b и c – стороны треугольника

r – радиус вписанной окружности

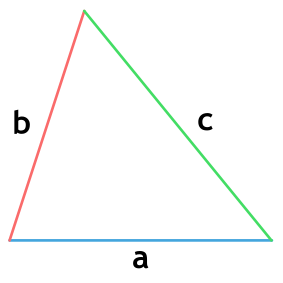
Площадь треугольника по формуле Герона

{S = sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)}}
{p= dfrac{a+b+c}{2}}

a, b и c – стороны треугольника

p – полупериметр треугольника

Площадь прямоугольного треугольника

Прямоугольный треугольник — это треугольник, в котором один угол прямой (равен 90 градусов).

Площадь прямоугольного треугольника через катеты

{S = dfrac{1}{2} cdot a cdot b}

a и b – стороны треугольника

Площадь прямоугольного треугольника через гипотенузу и прилежащий угол

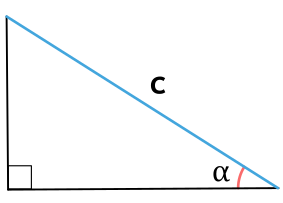
{S = dfrac{1}{4} cdot c^2 cdot sin{(2 alpha)}}

c – гипотенуза прямоугольного треугольника

α – прилежащий к гипотенузе c угол

Площадь прямоугольного треугольника через катет и прилежащий угол

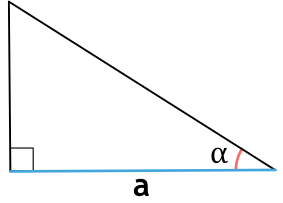
{S = dfrac{1}{2} cdot a^2 cdot tg{(alpha)}}

a – катет прямоугольного треугольника

α – прилежащий к катету a угол

Площадь прямоугольного треугольника через радиус вписанной окружности и гипотенузу

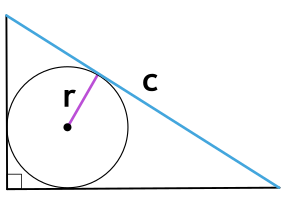
{S = r cdot (r+c)}

r – радиус вписанной окружности

c – гипотенуза прямоугольного треугольника

Площадь прямоугольного треугольника через вписанную окружность

{S = c_1 cdot c_2}

с₁ и с₂ – отрезки, полученные делением гипотенузы точкой касания окружности

Площадь прямоугольного треугольника по формуле Герона

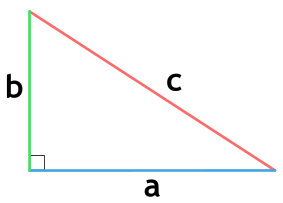
{S = (p-a) cdot (p-b)}
{p= dfrac{a+b+c}{2}}

a, b и c – стороны треугольника

p – полупериметр треугольника

Площадь прямоугольного треугольника через катет и гипотенузу

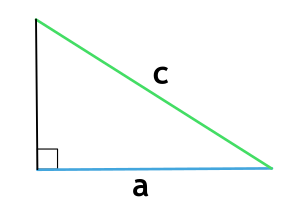
{S = dfrac{1}{2} cdot a cdot sqrt{c^2 – a^2}}

a – катет прямоугольного треугольника

c – гипотенуза прямоугольного треугольника

Площадь равнобедренного треугольника

Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по длине.

Площадь равнобедренного треугольника через основание и сторону

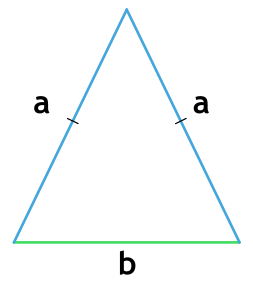
{S = dfrac{b}{4} sqrt{4a^2 – b^2}}

a – боковая сторона равнобедренного треугольника

b – основание равнобедренного треугольника

Площадь равнобедренного треугольника через основание, сторону и угол

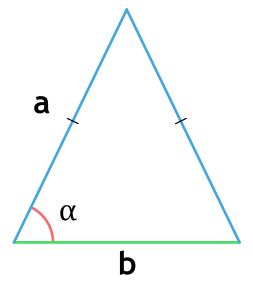
{S = dfrac{1}{2} cdot a cdot b cdot sin{(alpha)}}

a – боковая сторона равнобедренного треугольника

b – основание равнобедренного треугольника

α – угол между основанием и боковой стороной

Площадь равнобедренного треугольника через основание и высоту

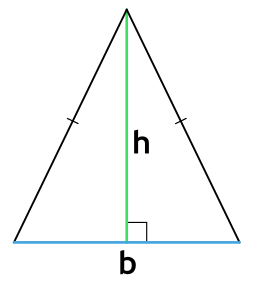
{S = dfrac{1}{2} cdot b cdot h}

b – основание равнобедренного треугольника

h – высота, проведенная к основанию равнобедренного треугольника

Площадь равнобедренного треугольника через боковые стороны и угол между ними

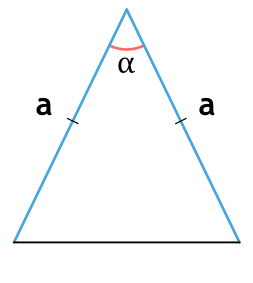
{S = dfrac{1}{2} cdot a^2 cdot sin(alpha)}

a – боковые стороны равнобедренного треугольника

α – угол между боковыми сторонами

Площадь равнобедренного треугольника через основание и угол между боковыми сторонами

{S = dfrac{b^2}{4 cdot tg {( dfrac{alpha}{2} )}}}

b – основание равнобедренного треугольника

α – угол между боковыми сторонами

Площадь равностороннего треугольника

Равносторонний треугольник – треугольник, у которого все стороны равны.

Площадь равностороннего треугольника через сторону

{S = dfrac{sqrt{3} cdot a^2}{4}}

a – сторона равностороннего треугольника

Площадь равностороннего треугольника через высоту

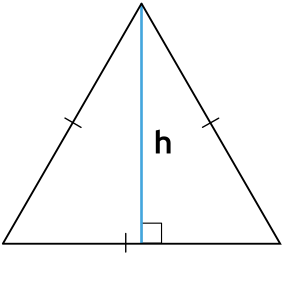
{S = dfrac{h^2}{sqrt{3}}}

h – высота равностороннего треугольника

Площадь равностороннего треугольника через радиус описанной окружности

{S = dfrac{3 sqrt{3} cdot R^2}{4}}

R – радиус описанной окружности

Площадь равностороннего треугольника через радиус вписанной окружности

{S = 3 sqrt{3} cdot r^2}

r – радиус описанной окружности

Примеры задач на нахождение площади треугольника

Задача 1

Найдите площадь треугольника со сторонами 13 14 15.

Решение

Для решения задачи воспользуемся формулой Герона.

S = sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)}

Для начала нам необходимо найти полупериметр p:

p= dfrac{a+b+c}{2}p= dfrac{13+14+15}{2}= dfrac{42}{2} = 21

Теперь можем подставить его в формулу Герона и найти ответ:

S = sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)} = sqrt{21 cdot (21-13) cdot (21-14) cdot (21-15)} = sqrt{21 cdot (8) cdot (7) cdot (6)} = sqrt{21 cdot 336} = sqrt{7056} = 84 : см^2

Ответ: 84 см²

Убедимся в правильности решения с помощью калькулятора .

Задача 2

Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 100.

Решение

Воспользуемся формулой.

S = dfrac{1}{2} cdot a cdot sqrt{c^2 – a^2} = dfrac{1}{2} cdot 28 cdot sqrt{100^2 – 28^2} = dfrac{1}{2} cdot 28 cdot sqrt{10000 – 784} = dfrac{1}{2} cdot 28 cdot sqrt{9216} = dfrac{1}{2} cdot 28 cdot 96 = 14 cdot 96 = 1344 : см^2

Ответ: 1344 см²

Проверим ответ на калькуляторе .

Задача 3

Найдите площадь прямоугольного треугольника если его катет и гипотенуза равны соответственно 15 и 17.

Решение

Задача аналогична предыдущей, поэтому решение очень похоже.

S = dfrac{1}{2} cdot a cdot sqrt{c^2 – a^2} = dfrac{1}{2} cdot 15 cdot sqrt{17^2 – 15^2} = dfrac{1}{2} cdot 15 cdot sqrt{289 – 225} = dfrac{1}{2} cdot 15 cdot sqrt{64} = dfrac{1}{2} cdot 15 cdot 8 = 15 cdot 4 = 60 : см^2

Ответ: 60 см²

Проверка .

Задача 4

Найдите площадь прямоугольного треугольника, если гипотенуза его равна 40 см а острый угол равен 60°.

Решение

Для решения задачи воспользуемся формулой.

S = dfrac{1}{4} cdot c^2 cdot sin{(2 alpha)} = dfrac{1}{4} cdot 40^2 cdot sin{(2 cdot 60°)} = dfrac{1}{4} cdot 1600 cdot sin{(120°)} = 400 cdot dfrac{sqrt{3}}{2} = 200 sqrt{3} : см^2 approx 346.41016 : см^2

Ответ: 200 sqrt{3} : см^2 approx 346.41016 : см^2

Проверка .

Задача 5

Найдите площадь равнобедренного треугольника, если боковая сторона равна 7 см а основание 4 см.

Решение

В этой задаче используем формулу для нахождения площади равнобедренного треугольника через основание и боковую сторону.

S = dfrac{b}{4} sqrt{4a^2 – b^2} = dfrac{4}{4} sqrt{4 cdot 7^2 – 4^2} = sqrt{4 cdot 49 – 16} = sqrt{196 – 16} = sqrt{180} = sqrt{36 cdot 5} = 6sqrt{5} : см^2 approx 13.41641 : см^2

Ответ: 6sqrt{5} : см^2 approx 13.41641

Проверка .

Задача 6

Найдите площадь равнобедренного треугольника, если его основание равно 30, боковая сторона равна 17.

Решение

Решим эту задачу по анологии с предыдущей.

S = dfrac{b}{4} sqrt{4a^2 – b^2} = dfrac{30}{4} sqrt{4 cdot 17^2 – 30^2} = dfrac{30}{4} sqrt{4 cdot 289 – 900} = dfrac{30}{4} sqrt{1156 – 900} = dfrac{30}{4} sqrt{256} = dfrac{30}{4} cdot 16= 30 cdot 4 = 120 : см^2

Ответ: 120 см²

Проверка .

Задача 7

Найдите площадь равностороннего треугольника со стороной 12 см.

Решение

Используем для решения задачи формулу.

S = dfrac{sqrt{3} cdot a^2}{4} = dfrac{sqrt{3} cdot 12^2}{4} = dfrac{sqrt{3} cdot 144}{4} = 36 sqrt{3} : см^2 approx 62.35383 : см^2

Ответ: 36 sqrt{3} : см^2 approx 62.35383 : см^2

Проверка .

Источник