Как найти площадь треугольника зная векторы - Сайт, где вы сможете решить свои вопросы

Калькулятор онлайн.
Вычисление площади треугольника построенного на векторах.

Этот калькулятор онлайн вычисляет площадь треугольника построенного на векторах. Треугольник может быть задан координатами двух векторов или
координатами трех вершин треугольника.

Онлайн калькулятор для вычисления площади треугольника построенного на векторах не просто даёт ответ задачи, он приводит подробное решение с
пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.

Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и
экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре.
А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее
сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным
решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень
образования в области решаемых задач повышается.

Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.

Правила ввода чисел

Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.

Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5 или так 1,3

Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.

Знаменатель не может быть отрицательным.

При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: ( -frac{2}{3} )

Целая часть отделяется от дроби знаком амперсанд: &
Ввод: -1&5/7
Результат: ( -1frac{5}{7} )

Наши игры, головоломки, эмуляторы:

Немного теории.

Определение векторного произведения векторов

Определение
Векторы ( vec{a}, ; vec{b} ) и ( vec{c} ) называются компланарными, если они лежат в одной плоскости
или параллельных плоскостях.

Определение
Тройка векторов называется упорядоченной, если указано, какой из них считается первым, вторым и третьим.

Например, в записи ( ( vec{a} ; vec{b} ; vec{c} ) ) вектор ( vec{a} ) считается первым, ( vec{b} )
– вторым, ( vec{c} ) – третьим.

Определение
Упорядоченная тройка некомпланарных векторов называется правой, если после приведения их к общему началу из конца третьего
вектора кратчайший поворот от первого ко второму виден совершающимся против часовой стрелки. В противном случае тройка векторов
называется левой.

Определение
Векторным произведением вектора ( vec{a} ) на вектор ( vec{b} ) называется вектор
( vec{a} times vec{b} ), который определяется тремя условиями:
1) длина вектора ( vec{a} times vec{b} ) равна ( |vec{a}| |vec{b}| sin varphi ), где ( varphi )
– угол между векторами ( vec{a} ) и ( vec{b} )
2) вектор ( vec{a} times vec{b} ) перпендикулярен каждому из векторов ( vec{a} ) и ( vec{b} )
3) векторы ( vec{a}, ;; vec{b}, ;; vec{a} times vec{b} ) образуют правую тройку векторов

Заметим, что условия 2 и 3 относятся к случаю, когда ( |vec{a}| |vec{b}| sin varphi neq 0 ), т.е. вектор
( vec{a} times vec{b} neq vec{0} ). Если же ( |vec{a}| |vec{b}| sin varphi = 0 ), то векторное произведение
определяется только условием 1: в этом случае ( vec{a} times vec{b} = 0 )

Основные свойства векторного произведения векторов

1. Если ( vec{a} ) и ( vec{b} ) – коллинеарные векторы, то ( vec{a} times vec{b} = 0 )

2. Длина векторного произведения неколлинеарных векторов ( vec{a} ) и ( vec{b} ) равна площади параллелограмма,
построенного на этих векторах.

3. ( vec{a} times vec{b} = – vec{b} times vec{a} ) свойство антиперестановочности сомножителей

4. ( ( alpha vec{a} ) times vec{b} = alpha ( vec{b} times vec{a} ) ) свойство сочетательности по отношению к
скалярному произведению

5. ( ( vec{a}+vec{b} ) times vec{c} = vec{a} times vec{c} + vec{b} times vec{c} ) свойство распределительности
относительно суммы векторов.

Выражение векторного произведения через координаты векторов

Теорема
Если векторы ( vec{a} ) и ( vec{b} ) заданы своими координатами:
( vec{a} left( a_x; a_y; a_z right), ;; vec{b} left( b_x; b_y; b_z right) ), то векторное произведение
векторов вычисляется по формуле:
( vec{a} times vec{b} = left( a_y b_z – b_y a_z ; ; ; a_z b_x – b_z a_x ; ; ; a_x b_y – b_x a_y right) )

Эту формулу с помощью определителей второго порядка можно записать в виде
( vec{a} times vec{b} = left( begin{vmatrix} a_y & a_z \ b_y & b_z end{vmatrix} ; ; ;
begin{vmatrix} a_z & a_x \ b_z & b_x end{vmatrix} ; ; ; begin{vmatrix} a_x & a_y \ b_x & b_y end{vmatrix} right) )

Источник

Самый простой многоугольник и вектор

Чтобы найти площадь треугольника через векторы и известные координаты его вершин, необходимо подробнее познакомиться с этими геометрическими объектами. Знание их свойств позволяет легко вычислять разные характеристики изучаемой фигуры, включая периметр, высоту, углы при вершинах и другие. При этом используются универсальные математические операции, которые можно применять с успехом не только для треугольника, но и для других многоугольников.

Фигура на плоскости

Треугольник в геометрии представляет собой самый простой многоугольник, который лежит всегда в одной плоскости, даже если фигура рассматривается в трехмерном пространстве. Состоит он из сторон и вершины.

Сторон и вершин у фигуры по три. Сторона является отрезком, а вершина — это точка пересечения этих отрезков. Для нее характерен определенный угол. Все углы треугольника являются разными в общем случае, их сумма всегда соответствует 180°. Однако, существуют специальные типы фигуры, для которых либо два угла равны друг другу (равнобедренный), либо все три (равносторонний). В задачах называют треугольники по имени их трех вершин, обозначенных латинскими буквами, например, ABC или NPQ.

Для треугольника важное значение имеют следующие отрезки:

делящий противоположную углу сторону пополам — медиана;
разделяющий угол при вершине на два равных — биссектриса;
падающий под прямым углом на противоположную углу сторону — высота.

Высота, например, используется для расчета площади фигуры. Для равностороннего треугольника все эти отрезки совпадают друг с другом для любой вершины, а для равнобедренного они одинаковы лишь для угла, образованного равными сторонами.

Направленный отрезок

Вектором называют линейный элемент, который имеет начало и конец. Для его определения удобнее всего использовать координатную плоскость. Она представляет собой две направленные оси, имеющие шкалу и пересекающиеся под углом 90°. Точка пересечения является началом координат и обозначается буквой O (0; 0). Здесь каждая из цифр указывает точку пересечение перпендикуляра, опущенного из рассматриваемого объекта к каждой из двух осей.

Если начало A (x0; y0) и конец B (x1; y1) вектора известны, тогда легко можно вычислить его собственные координаты. Делается это так:

AB- = B-A = (x1-x0; y1-y0).

Иными словами, чтобы получить вектор AB-, следует из соответствующих координат его конца вычесть его начало. Эта операция эквивалентна параллельному перемещению AB- в начало координатной плоскости, что говорит о существовании бесконечного количества одинаковых AB-векторов.

Направленные отрезки можно складывать, вычитать и умножать. Для каждой из операций существуют определенные правила. Если для сложения и вычитания речь идет о геометрических особенностях, то в случае умножения применяются исключительно алгебраические выражения. Вектор a- можно умножить на b- двумя принципиально разными способами:

Скалярно: (a-*b-). В этом случае мы получаем число. Правило умножения записывается следующим образом: (a-*b-) = |a-|*|b-|*cos (ab)=x1*x2+y1*y2. Здесь знаком модуля (||) обозначены длины соответствующих отрезков, cos (ab) — это косинус угла между a- и b-, при этом a-(x1; y1), b-(x2; y2). Этот тип произведения можно использовать для вычисления углов между направленными отрезками, а также для определения объема фигур в пространстве.
Векторно: [a-*b-]. Результатом этой операции является вектор, который перпендикулярен исходным, его направление (вверх или вниз) принято определять по правилу правой руки: четыре пальца должны быть направлены от конца a- к концу b-, тогда оттопыренный большой палец укажет направление их векторного произведения. Длина этого перпендикулярного вектора определяется так: [a-*b-] = |a-|*|b-|*sin (ab) = x1*y2-x2*y1. Векторное произведение используют для вычисления площадей фигур.

Методы вычисления площади по координатам

Задачи на вычисление площадей, периметров или объемов фигур по известным координатам их вершин являются типичными для школьного курса геометрии. В связи с развитием современных технологий школьники часто ищут в интернете, как решить треугольник онлайн по координатам. Тем не менее, существует ряд простых способов, которые позволяют быстро найти площадь фигуры, если известно расположение трех его вершин на координатной плоскости.

Универсальный подход

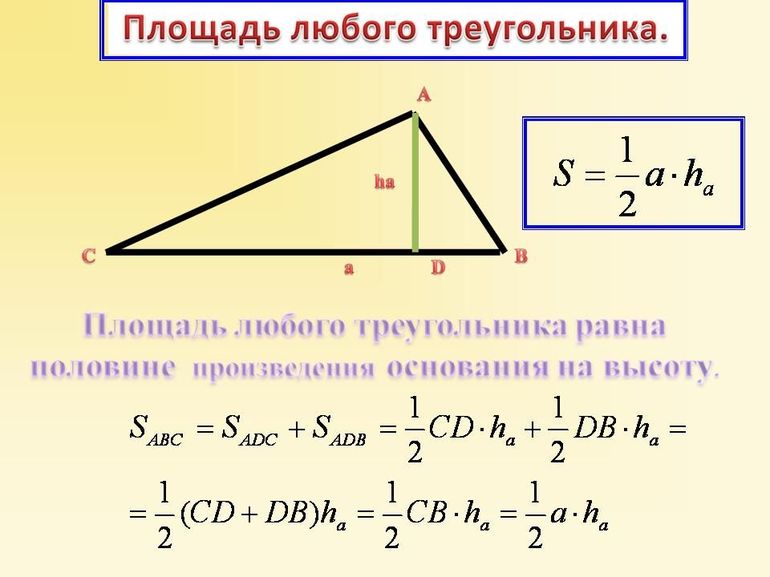
Этот метод можно применять всегда, независимо от того, какой тип треугольника рассматривается. Известно, что площадь фигуры вычисляется, как произведение половины стороны на опущенную на нее высоту: S = ½*a*h.

Пусть имеются координаты вершин заданного треугольника ABC:

A (x1; y1);
B (x2; y2);
C (x3; y3).

Тогда координаты его векторов AB- и AC- выразятся так:

AB- = (x2-x1; y2-y1);
AC- = (x3-x1; y3-y1).

Если провести высоту h треугольника ABC к любой из этих сторон, например, к AC, то ее длина может быть рассчитана с использованием тригонометрической функции синуса:

h = AB*sin (α).

Здесь α является углом между векторами-сторонами AB- и AC-. Тогда формулу площади можно переписать в следующем виде: S = ½*a*h = ½*AC* AB*sin (α).

Можно заметить, что записанное выражение является не чем иным, как векторным произведением для AB- и AC-, поэтому можно переписать формулу для S так:

S = ½*[ AB-* AC- ] = ½*((x2-x1)*(y3-y1) — (y2-y1)*(x3-x1)).

Можно аналогично показать, что подобные выражения получаются для пар векторов AC-, BC- и AB-, BC-.

Рекомендуется не запоминать конечные выражения для площади треугольника, поскольку они являются несколько громоздкими, и при их использовании ученики могут запутаться. Для решения подобного рода задач достаточно понять свойства векторов и единственную универсальную формулу для S для любого типа треугольников.

Любопытно отметить, что векторное произведение при вычислении площади можно применять не только для треугольников, но и для любых четырехугольников. Так, в случае параллелограмма рассматриваемая характеристика будет точно равна векторному произведению любых смежных (непараллельных) его сторон.

Использование формулы Герона

Этот способ также может считаться универсальным, поскольку он применим к любым типам треугольников. В работе Герона Александрийского, которая называется «Метрика» и относится к I веку нашей эры, впервые было обнаружено выражение, позволяющее по длинам сторон рассматриваемой фигуры определить ее площадь. Формула имеет следующий вид:

S = (p*(p-a)*(p-b)*(p-c))^0,5.

Здесь p — полупериметр, a, b, c — длины сторон.

Последовательность этапов решения задачи можно выразить таким образом:

Необходимо определить координаты векторов, образующих стороны треугольника.
Затем, следует вычислить длины их сторон.
Посчитать полупериметр фигуры.
Применить формулу Герона.

Ключевым этапом является определение длины вектора. Пусть AB- имеет координаты (x1; y1), тогда его длина вычисляется так:

|AB-| = (x1² + y1²)^0,5.

Длина любого вектора как на плоскости, так и в пространстве, вычисляется, как сумма квадратов всех его координат, взятых под корень.

Очевидно, что можно записать общее выражение для площади треугольника через координаты с использованием формулы Герона, но оно будет слишком громоздким, поэтому нет никакого смысла запоминать его.

Другие способы

Существуют эмпирические правила, которые можно запомнить и легко решать задачи на определение площади треугольника. Пусть координаты его вершин задаются так: A (x1; y1), B (x2; y2), C (x3; y3). Предположим, что порядок вершин A, B, C расположен против часовой стрелки, тогда существуют следующие правила определения площади ABC:

Можно воспользоваться формулой: S = ½*(x1*(y2-y3) + x2*(y3-y1) + x3*(y1-y2)). То есть выбирается первая координата вершины и умножается на разность вторых координат двух других вершин, возникающих против хода стрелки часов от первой. Затем, все три члена складываются и делятся на 2.
Матричный способ. Необходимо выписать в столбик пары координат каждой вершины против часовой стрелки и завершить координатами исходной. После этого следует сложить три попарных произведения первой и второй координат двух соседних вершин, а затем, вычесть три попарных произведений второй и первой координат тех же вершин. Результат поделить пополам. Например: (x1; y1) (x2; y2) (x3; y3) (x1; y1). S = ½*(x1*y2 + x2*y3 + x3*y1 — y1*x2 — y2*x3 — y3*x1).

Решение задачи

Дана фигура АВС. Найдите площадь треугольника, вершины которого имеют координаты A (1; -3), B (2; 5), C (-2; -2).

Для нахождения решения следует обратиться за помощью к универсальному способу. Сначала необходимо выбрать два вектора, образующих стороны треугольника. Пусть это будут AB- и BC-. Теперь нужно знать их координаты. Они равны:

AB- = (2−1; 5-(-3)) = (1; 8);
BC- = (-2−2; -2−5) = (-4; -7).

Чтобы рассчитать площадь, достаточно вычислить полупроизведение векторное для выбранных направленных отрезков: S = ½*[AB-*BC-] = ½*(1*(-7)-8*(-4)) = 12,5 квадратных единиц.

Таким образом, существует несколько методик вычисления площади треугольника, если известны координаты его вершин. Все они сводятся к использованию свойств векторов и известных формул. Существуют также выражения, которые следует запомнить, чтобы решать подобные задачи.

Источник

Содержание

1. Площадь в геометрии
2. Площадь по координатам вершин или двух определяющих его векторов
3. Площадь в матричном виде
4. Площадь в тензорном исчислении
5. Площадь треугольника в трехмерном пространстве
6. Через проекции площадей на координатные плоскости
7. Использованием операции векторного произведения векторной алгебры
8. Площадь с использованием операций свертки тензорного исчисления

В математике и физике широко пользуются тензорным исчислением, в которой понятия “скаляр”, “вектор” и “тензор” являются широко употребляемыми объектами. Смысл этих понятий и анализ первых двух понятий был определен в предыдущей статье, и последующей . В первой были определены понятия “длины ” вектора и “скалярного” произведения векторов и некоторые определения, с ними связанные, их геометрический смысл, а во второй введены понятия и определения, связанные с тензорами. Без них любая статья подобного направления будет художественным текстом на иностранном языке без перевода.

Под понятием “тензор ” обычно понимаются объекты типа “вектор “, “матрица “, и другие многоиндексные объекты произвольной валентности с размерностью, равной размерности n рассматриваемого пространства:

где i .. j , k .. m – индексы тензора,
m –символ последнего индекса.

Тензоры в математике применяются очень широко. В частности, с их помощью можно определять геометрические параметры – длину, площадь, объем. А также различные “прекции”. А для многомерных объектов – гиперобъемы. Длину вектора или отрезка и проекции мы определили в предыдущих статьях. Здесь определим площади.

1. Площадь в геометрии

Из школьной геометрии мы знаем, что площадь квадрата со сторонами d равна d ² .
Площадь прямоугольника со сторонами a и b равна ab .
Площадь треугольника со стороной a и высотой h равна ah /2.
Площадь треугольника со сторонами a и b равна a · b · sin ( a , b ).

2. Площадь по координатам вершин или двух определяющих его векторов

А чему равна площадь треугольника, заданного с помощью координат ее вершин или двух известных определяющих его сторон–векторов? Конечно, можно вычислить, применяя геометрический метод. Но есть еще один метод – универсальный, годный при любом расположении ее вершин и сторон–векторов. Попробуем найти эту формулу для двумерного случая.

Задача: найти площадь треугольника OAB .

Решение: ACB )площадь треугольника ОАВ равна площади квадрата OYa CXb = Ya Xb за вычетом окружающих треугольник OAB треугольников

S = S(OYb B) + S(BCA) + S(OAXa ).

Вычислим их:

S(OYb B) = (OYb) *(OXb) = Yb Xb,
S(OXa A) = (OXa )*( Ya ) = Xa Ya,
S(BCA) = (Yb – Ya )*( Xa – Xb ) = Yb Xa – Yb Xb – Ya Xa + Ya Xb.

Сложим ( точнее – вычтем ) их :

После приведения подобных членов имеем:

S = ½(Yb Xa – Ya Xb) = A × B.

Это очень замечательная формула, по которой, зная координаты вектора, можно напрямую вычислить площадь треугольника и четырехугольника, построенных на них. При этом получим скалярную – точнее, псевдоскалярную – величину. Псевдоскалярную – потому что, если поменять местами вектора A и B , то результат поменяет свой знак – можете поверить – а можете проверить.

Но у этой формулы имеется недостаток – она годится только на двумерной плоскости.

3. Площадь в матричном виде

Есть еще одна математическая дисциплина, которая позволяет ее методами вычислить площадь треугольника по значениям двух матриц-векторов. В виде формулы она представляется через представление площади как детерминанта матрицы, составленного из элементов этих векторов, в таком виде:

У этой формулы также имеется недостаток – она годится только на двумерной плоскости.

4. Площадь в тензорном исчислении

Эта замечательная формула записана не в тензорном формате. Но она состоит из тензорных элементов, элементы которой определяются как элементы прямого произведения элементов векторов A и B . Для того, чтобы получить скаляр, в тензорном исчислении необходимо свернуть все индексы тензора. Поэтому в тензорном виде площадь записывается в форме, где ε ᵢ ⱼ – антисиммметричный тензор:

5. Площадь треугольника в трехмерном пространстве

В трехмерном случае обойтись такими простыми формулами будет невозможно – алгоритмы будут немножко сложнее. В трехмерном пространстве два вектора будут иметь уже по три координаты – ( x , y , z ). Здесь можно выделить основных метода.

Первый метод – используя двухмерные параметры треугольника – находим соответствующие параметры треугольника (длины сторон, углы, координаты точек A и B в плоскости, где находится треугольник) и применяем любые из выше показанных методов (есть, конечно, и другие методы).

Второй метод – используя непосредственно трехмерные параметры треугольника.

6. Через проекции площадей на координатные плоскости

Например, так. Первой операцией будет нахождение площадей получающегося треугольника в координатных плоскостях S(yz), S(zx) и S(xy). Это можно сделать любым из показанных выше методов. В результате получим проекции площадей треугольника на соответствующие координатные плоскости. Причем три проекции {S(yz), S(zx), S(xy)} составлять координаты некоторого вектора [S(yz), S(zx), S(xy)]. Точнее, опять – псевдовектора или по другому – аксиального вектора . Псевдовектор меняет свой знак при преобразовании отражения осей координат.

А общая площадь получится как длина этого вектора. А длину вектора проходили ранее .

7. Использованием операции векторного произведения векторной алгебры

Есть такая математическая дисциплина, которая называется векторной алгеброй , в которой определена операция 3-мерного векторного умножения, результат которой есть именно определенный только что (п.7) вектор:

C ₃ = A × B = [S(yz), S(zx), S(xy)] = ( Az By – Ay Bz , Ax Bz – Az Bx , Ay Bx – Ax By,) .

А общая площадь получится, как писали там же, как длина этого вектора. Как отмечали выше, этот вектор не совсем обычный – а псевдовектор.

8. Площадь с использованием операций свертки тензорного исчисления

Для этого используем формулу площади треугольника через длину сторон и угол между ними: площадь треугольника со сторонами a и b равна a · b · sin ( a , b ). Найдем участвующие в формуле параметры через скалярные произведения. Длины векторов равны | a | и | b |, а также

В результате получили выражение, состоящее только из скалярных произведений участвующих в формуле параметров треугольника – векторов его сторон a и b. Только в формуле опущены индексы.

И эта формула может быть применена в пространстве любой размерности, а не только размерности 2 и 3.

Если статья понравилась – ставьте лайк, делитесь в ваших соцсетях.
И комментируйте!

Источник

Как найти площадь треугольника по координатам его вершин?

1способ:

Найти длины трёх сторон треугольника и вычислить площадь по формуле Герона. Способ удобен, если длины сторон являются целыми числами. В противном случае предстоят громоздкие вычисления.

2 способ:

вывести формулу для нахождения площади и использовать её для вычисления.

Утверждение

Площадь треугольника ABC с вершинами в точках A(x₁;y₁), B(x₂;y₂), C(x₃;y₃) можно вычислить с помощью формулы

$[S_{Delta ABC} = frac{1}{2}left| {(x_2 - x_1 )(y_3 - y_1 ) - (x_3 - x_1 )(y_2 - y_1 )} right|.]$

Доказательство:

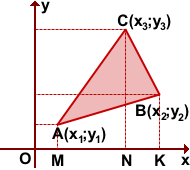Рассмотрим треугольник ABC,

A(x₁;y₁), B(x₂;y₂), C(x₃;y₃)

Опустим перпендикуляры из вершин треугольника на координатные оси.

$[S_{Delta ABC} = S_{MACN} + S_{NCBK} - S_{MABK} ]$

$[S_{MACN} = frac{{MA + CN}}{2} cdot MN = frac{{y_1 + y_3 }}{2} cdot (x_3 - x_1 ),]$

$[S_{NCBK} = frac{{NC + BK}}{2} cdot NK = frac{{y_3 + y_2 }}{2} cdot (x_2 - x_3 ),]$

$[S_{MABK} = frac{{MA + BK}}{2} cdot MK = frac{{y_1 + y_2 }}{2} cdot (x_2 - x_1 ).]$

$[S_{Delta ABC} = ]$

$[= frac{{y_1 + y_3 }}{2} cdot (x_3 - x_1 ) + frac{{y_3 + y_2 }}{2} cdot (x_2 - x_3 ) - frac{{y_1 + y_2 }}{2} cdot (x_2 - x_1 ) = ]$

$[= frac{1}{2}[(y_1 + y_3 )(x_3 - x_1 ) + (y_3 + y_2 )(x_2 - x_3 ) - (y_1 + y_2 )(x_2 - x_1 )] = ]$

$[= frac{1}{2}[x_3 y_1 - x_1 y_1 underline { + x_3 y_3 } - x_1 y_3 + x_2 y_3 underline { - x_3 y_3 } + x_2 y_2 - x_3 y_2 - ]$

$[= frac{1}{2}[(x_2 y_3 - x_2 y_1 ) + ( - x_1 y_3 + x_1 y_1 ) + (x_1 y_2 - x_1 y_1 ) + ]$

$[= frac{1}{2}[x_2 (y_3 - y_1 ) - x_1 (y_3 - y_1 ) + x_1 (y_2 - y_1 ) - x_3 (y_2 - y_1 )] = ]$

$[= frac{1}{2}[(x_2 - x_1 )(y_3 - y_1 ) - (x_3 - x_1 )(y_2 - y_1 )].]$

С учетом вариантов взаимного расположения точек A, B и C формула для вычисления площади треугольника по координатам его вершин приобретает вид:

$[ S_{Delta ABC} = frac{1}{2}left| {(x_2 - x_1 )(y_3 - y_1 ) - (x_3 - x_1 )(y_2 - y_1 )} right|. ]$

Что и требовалось доказать.

3 способ:

Найти длины двух сторон и косинус угла между ними и вычислить площадь треугольника через стороны и синус угла между ними.

4 способ:

Найти длину и уравнение одной стороны треугольника и длину высоты, проведённой к этой стороне. Вычислить площадь через сторону и высоту.

Рассмотрим эти способы на конкретном примере.

Найти площадь треугольника, вершины которого имеют координаты A(-1;-3), B(3;4), C(5;-5).

1 способ:

Находим длины сторон треугольника ABC.

$[AB = sqrt {(x_B - x_A )^2 + (y_B - y_A )^2 } ]$

$[ AB = sqrt {(3 - ( - 1))^2 + (4 - ( - 3))^2 } = sqrt {16 + 49} = sqrt {65} ;]$

$[AC = sqrt {(x_C - x_A )^2 + (y_C - y_A )^2 } ]$

$[AC = sqrt {(5 - ( - 1))^2 + ( - 5 - ( - 3))^2 } = sqrt {36 + 4} = sqrt {40} ;]$

$[BC = sqrt {(x_C - x_B )^2 + (y_C - y_B )^2 } ]$

$[BC = sqrt {(5 - 3)^2 + ( - 5 - 4)^2 } = sqrt {4 + 81} = sqrt {85} .]$

Поскольку длины сторон выражены иррациональными числами, вычислять площадь треугольника по формуле Герона — не самый лучший способ.

2 способ:

Подставляем в формулу x₁=-1, y₁=-3, x₂=3, y₂=4, x₃=5, y₃=-5:

$[S_{Delta ABC} = frac{1}{2}left| {(3 - ( - 1))( - 5 - ( - 3)) - (5 - ( - 1))(4 - ( - 3))} right| = ]$

$[= frac{1}{2}left| {4 cdot ( - 2) - 6 cdot 7} right| = frac{1}{2} cdot 50 = 25.]$

3 способ:

Угол A образован векторами AC и AB. Отсюда

$[ cos angle A = frac{{overrightarrow {AB} cdot overrightarrow {AC} }}{{left| {overrightarrow {AB} } right| cdot left| {overrightarrow {AC} } right|}} ]$

Находим координаты векторов:

$[overrightarrow {AB} (x_B - x_A ;y_B - y_A )]$

$[overrightarrow {AC} (x_C - x_A ;y_C - y_A )]$

Скалярное произведение

Длины AB и AC уже знаем:

$[cos angle A = frac{{10}}{{sqrt {65} cdot sqrt {40} }} = frac{{10}}{{sqrt {5 cdot 13} cdot sqrt {5 cdot 4 cdot 2} }} = ]$

$[= frac{{10}}{{5 cdot 2sqrt {26} }} = frac{1}{{sqrt {26} }}.]$

Синус и косинус одного угла связаны соотношением:

Синус угла от 0° до 180° является положительным числом, поэтому

$[sin angle A = sqrt {1 - cos ^2 angle A} ]$

$[sin angle A = sqrt {1 - frac{1}{{26}}} = sqrt {frac{{25}}{{26}}} = frac{5}{{sqrt {26} }}.]$

Отсюда

$[S_{Delta ABC} = frac{1}{2} cdot AB cdot AC cdot sin angle A,]$

$[S_{Delta ABC} = frac{1}{2} cdot sqrt {65} cdot sqrt {40} cdot frac{5}{{sqrt {26} }} = 25.]$

4 способ:

Найдём уравнение прямой AB. Подставляем координаты A и B в уравнение y=kx+b:

$[left{ begin{array}{l} - 3 = k cdot ( - 1) + b \ 4 = k cdot 3 + b \ end{array} right.]$

Отсюда k=7/4, b=-5/4

$[y = frac{7}{4}x - frac{5}{4},4y = 7x - 5,]$

Найдём расстояние от точки C до прямой AB:

$[d = frac{{left| {7 cdot 5 - 4 cdot ( - 5) - 5} right|}}{{sqrt {7^2 + 4^4 } }} = frac{{50}}{{sqrt {65} }}.]$

Это расстояние равно высоте треугольника, проведённой из вершины C к стороне AB. Отсюда

$[S_{Delta ABC} = frac{1}{2} cdot AB cdot d = frac{1}{2} cdot sqrt {65} cdot frac{{50}}{{sqrt {65} }} = 25.]$

Источник

Площадь треугольника

,
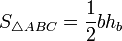
так как

,
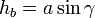
то:
—
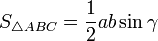
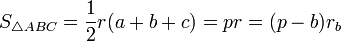
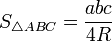
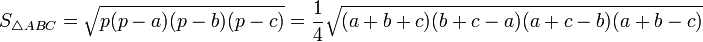
формула
Герона
—
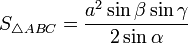
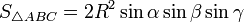
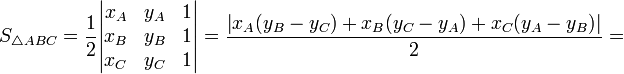
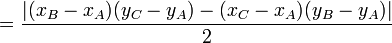
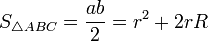
для прямоугольного
треугольника
—
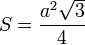
для равностороннего
треугольника
—
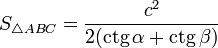
если треугольник
задан по стороне и двум прилежащим к
ней углам
—
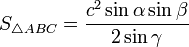
если треугольник
задан по стороне и двум прилежащим к
ней углам
—
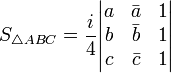
ориентированная
площадь треугольника на комплексной
плоскости с вершинами в a, b, c.

Где:

—
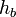
высота, проведённая
на сторону

,
—
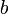
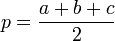
полупериметр,
—
радиус вписанной
окружности,
—
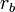
радиус вневписанной
окружности,
касающейся стороны

,
—
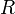
радиус описанной
окружности,
—
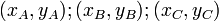
координаты вершин
треугольника.

Для
площади справедливы неравенства:

,
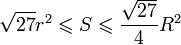
причём оба равенства достигаются.
,
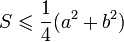
где равенство достигается для
равнобедренного прямоугольного
треугольника.

Вычисление площади треугольника в пространстве с помощью векторов

Пусть
вершины треугольника находятся в точках

Введём
вектор площади

.
Длина этого вектора равна площади
треугольника, а направлен он по нормали
к плоскости треугольника:

Положим

,
где

,

—
проекции треугольника на координатные
плоскости. При этом

и аналогично

Площадь
треугольника равна

.

Альтернативой
служит вычисление длин сторон (по теореме
Пифагора)
и далее по формуле
Герона.

Площадь
параллелограмма

,
где a — сторона, h — высота проведенная
к этой стороне.

,
где a и b — стороны, а

—
угол между сторонами a и b.

,
где p — полупериметр, r — радиус вписанной
окружности

20)

Объём
пирамиды может быть вычислен по формуле:

где

—
площадь
основания и

—
высота;

Прямой
параллелепипед

Объём
V=S_о*h

Прямоугольный
параллелепипед

Объём
V=abc, где a, b, c — измерения прямоугольного
параллелепипеда.

Куб

Объём
V=a³

21)

Уравнения
плоскости

Плоскость —
алгебраическая
поверхность
первого порядка: в декартовой
системе координат
плоскость может быть задана уравнением
первой степени.

Общее
уравнение (полное) плоскости

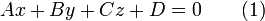
где

—
постоянные, причём

и

одновременно
не равны нулю; в векторной
форме:

где

—
радиус-вектор точки

,
вектор

перпендикулярен
к плоскости (нормальный вектор).
Направляющие
косинусы
вектора

:

Если
один из коэффициентов в уравнении
плоскости равен нулю, уравнение называется
неполным.
При

плоскость
проходит через начало
координат,
при

(или

)
П. параллельна оси

(соответственно

или

).
При

(
,
или

)
плоскость параллельна плоскости

(соответственно

или

Уравнение
плоскости в отрезках:

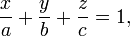
где

—
отрезки, отсекаемые плоскостью на осях

Уравнение
плоскости, проходящей через точку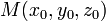

перпендикулярно
вектору нормали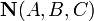

:

в
векторной форме:

Уравнение
плоскости, проходящей через три заданные
точки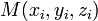

,
не
лежащие на одной прямой:

(смешанное
произведение векторов), иначе

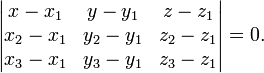
Нормальное
(нормированное) уравнение плоскости

в
векторной форме:

где

–
единичный вектор,

—
расстояние П. от начала координат.
Уравнение (2) может быть получено из
уравнения (1) умножением на нормирующий
множитель

(знаки

противоположны).

22)

Векторное
параметрическое уравнение прямой
в пространстве:

где

—
радиус-вектор
некоторой фиксированной точки

лежащей
на прямой,

—
ненулевой вектор,
коллинеарный
этой прямой (называемый её направляющим
вектором),

—
радиус-вектор
произвольной точки прямой.

Параметрическое
уравнение прямой
в пространстве:

где

—
координаты
некоторой фиксированной точки

лежащей
на прямой;

—
координаты
вектора,
коллинеарного
этой прямой.

Каноническое
уравнение прямой
в пространстве:

где

—
координаты
некоторой фиксированной точки

лежащей
на прямой;

—
координаты
вектора,
коллинеарного
этой прямой.

Общее
векторное уравнение прямой^[^{уточнить}^]
в пространстве:

Поскольку
прямая является пересечением двух
различных непараллельных
плоскостей,
заданных соответственно общими
уравнениями:

А1х
+ В1у + С1 = 0,

А2х
+ В2у + С2 = 0,

то
уравнение прямой можно задать системой
этих уравнений:

Уравнение
прямой в пространстве можно записать
в виде векторного
произведения
радиуса-вектора произвольной точки
этой прямой

на
фиксированный направляющий вектор
прямой

где
фиксированный вектор

,
ортогональный вектору

,
можно найти, подставляя в это уравнение
радиус-вектор какой-нибудь одной
известной точки прямой.

23)

Определение.
Любая
прямая на плоскости может быть задана
уравнением первого порядка

Ах
+ Ву + С = 0,

причем
постоянные А, В не равны нулю одновременно.
Это уравнение первого порядка называют
общим
уравнением прямой. В
зависимости от значений постоянных А,В
и С возможны следующие частные случаи:

• C
= 0, А ≠0, В ≠ 0 – прямая проходит через
начало координат

• А
= 0, В ≠0, С ≠0 { By + C = 0}- прямая параллельна
оси Ох

• В
= 0, А ≠0, С ≠ 0 { Ax + C = 0} – прямая параллельна
оси Оу

• В
= С = 0, А ≠0 – прямая совпадает с осью Оу

• А
= С = 0, В ≠0 – прямая совпадает с осью Ох

Уравнение
прямой может быть представлено в
различном виде в зависимости от каких
– либо заданных начальных условий.

24)

Пусть
плоскость

задана
уравнением

и
дана точка

.
Тогда расстояние

от
точки

до
плоскости

определяется
по формуле

(11.7)

Доказательство.
Расстояние от точки

до
плоскости

— это, по определению, длина перпендикуляра

,
опущенного из точки

на
плоскость

(рис. 11.9).

Рис.11.9.Расстояние
от точки до плоскости

Вектор

и
нормальный вектор n
плоскости

параллельны,
то есть угол

между
ними равен 0 или

,
если вектор n
имеет направление противоположное,
указанному на рис. 11.9. Поэтому

Откуда

(11.8)

Координаты
точки

,
которые нам неизвестны, обозначим

.
Тогда

.
Так как

,
то

.
Раскрыв скобки и перегруппировав
слагаемые, получим

(11.9)

Точка

лежит
на плоскости

,
поэтому ее координаты удовлетворяют
уравнению плоскости:

.
Отсюда находим, что

.
Подставив полученный результат в
формулу (11.9),
получим

.
Так как

,
то из формулы (11.8)
следует формула (11.7).

Пусть
плоскости

и

заданы
соответственно уравнениями

и

.
Требуется найти угол

между
этими плоскостями.

Плоскости,
пересекаясь, образуют четыре двугранных
угла (рис. 11.6): два тупых и два острых или
четыре прямых, причем оба тупых угла
равны между собой, и оба острых тоже
равны между собой. Мы всегда будем искать
острый угол. Для определения его величины
возьмем точку

на
линии пересечения плоскостей и в этой
точке в каждой из плоскостей проведем
перпендикуляры

и

к
линии пересечения. Нарисуем также
нормальные векторы

и

плоскостей

с
началами в точке

(рис.
11.6).

Рис.11.6.Угол
между плоскостями

Если
через точку

провести
плоскость

,
перпендикулярную линии пересечения
плоскостей

,
то прямые

и
изображения векторов

будут
лежать в этой плоскости. Сделаем чертеж
в плоскости

(возможны
два варианта: рис. 11.7 и 11.8).

Рис.11.7.Угол
между нормальными векторами острый

Рис.11.8.Угол
между нормальными векторами тупой

В
одном варианте (рис. 11.7)

и

,
следовательно, угол

между
нормальными векторами равен углу

,
являющемуся линейным углом острого
двугранного угла между плоскостями

Во
втором варианте (рис. 11.8)

,
а угол

между
нормальными векторами равен

.
Так как

то
в обоих случаях

.

По
определению скалярного произведения

.
Откуда

и
соответственно

(11.4)

Так
как координаты нормальных векторов
известны, если заданы уравнения
плоскостей, то полученная формула (11.4)
позволяет найти косинус острого угла
между плоскостями.

Если
плоскости перпендикулярны, то
перпендикулярны и их нормальные векторы.
Получаем условие перпендикулярности
плоскостей:

(11.5)

Если
плоскости параллельны, то коллинеарны
их нормальные векторы. Получаем условие
параллельности плоскостей

(11.6)

Угол
между прямыми. Угол между прямой и
плоскостью.

Угол
между прямыми в пространстве равен углу
между их направляющими векторами.
Поэтому, если две прямые заданы
каноническими уравнениями вида

косинус угла между ними можно найти по
формуле:

.
(8.14)

Условия
параллельности и перпендикулярности
прямых тоже сводятся к соответствующим
условиям для их направляющих векторов:

–
условие
параллельности прямых,
(8.15)

–
условие
перпендикулярности прямых.
(8.16)

Угол
φ между прямой, заданной каноническими
уравнениями

и
плоскостью, определяемой общим уравнением

Ax
+ By
+ Cz
+ D
= 0,

можно рассматривать как дополнительный
к углу ψ между направляющим вектором
прямой и нормалью к плоскости. Тогда

(8.17)

Условием
параллельности прямой и плоскости
является при этом условие перпендикулярности
векторов n
и а:

Al
+ Bm
+ Cn
=
0,
(8.18)

а
условием
перпендикулярности прямой и плоскости
– условие параллельности этих векторов:
A/l
= B/m
= C/n.

(8.19)

25)

Линейное,
или векторное
пространство

над
полем

—
это непустое
множество

,
на котором введены операции

сложения,
то есть каждой паре элементов множества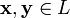

ставится
в соответствие элемент того же множества,
обозначаемый

и
умножения
на скаляр
(то есть элемент поля

),
то есть любому элементу

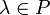
и
любому элементу

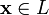
ставится
в соответствие единственный элемент
из

,
обозначаемый

.

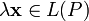
При
этом на операции накладываются следующие
условия:

,
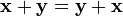
для любых

(коммутативность
сложения);
,
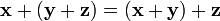
для любых

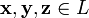
(ассоциативность
сложения);
существует
такой элемент

,
что

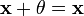
для
любого

(существование
нейтрального элемента относительно
сложения),
в частности

не
пусто;
для
любого

существует
такой элемент

,
что

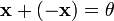
(существование
противоположного элемента относительно
сложения).
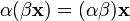
(ассоциативность
умножения на скаляр);
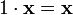
(унитарность:
умножение на нейтральный (по умножению)
элемент поля P сохраняет вектор).
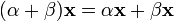
(дистрибутивность
умножения на вектор относительно
сложения скаляров);
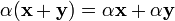
(дистрибутивность
умножения на скаляр относительно
сложения векторов).