Как найти площадь треугольного сечения тетраэдра - Сайт, где вы сможете решить свои вопросы

Геометрия. Объясните, пожалуйста, как найти площадь сечения тетраэдра.

мойше цехновицер

Ученик

(9),
на голосовании

7 лет назад

В тетраэдре DABC угол DBA = угол DBC = 90 градусов, DB = 6, AB = BC = 8, AC = 12. Постройте сечение тетраэдра плоскостью, проходящей через середину DB и параллельной плоскости ADC (построил). Найдите площадь сечения. Как это сделать?

Голосование за лучший ответ

Михаил Ужов

Эксперт пока не указал должность

7 лет назад

Две грани – прямоугольные треугольники. Стороны сечения – средние линии этих треугольников, равные половинам гипотенузы.
Гипотенуза равна √(DB²+AB²)=√(36+64)=10; Стороны равны по 5.
Третья сторона сечения равна половине АС, 12/2=6
А дальше – формула Герона:
р=(5+5+6)/2=8
S=√(8×3×3×2)=12

Юлия Коваленко

Мудрец

(18185)

7 лет назад

Можно и как сказал Михаил, но зачем такие сложности?

Допустим, обозначь точку сечения на стороне ВС как С1, на стороне АВ как А1, на стороне DВ как D1. У тебя получается, что СС1=С1В, АА1=А1В, DD1=D1B.Находишь D1B, С1В, А1В. По теореме Пифагора считаешь D1C1, А1D1. А1С1=1/2АС как средняя линия треугольника АВС. Итак, ты нашёл все стороны треугольника сечения и доказал, что он равнобедренный. Проводишь в нём высоту, считаешь её, по формуле S=1/2основания*высоту находишь его площадь.

Источник

Как найти площадь тетраэдра

Тетраэдром в стереометрии называется многогранник, который состоит из четырёх треугольных граней. Тетраэдр имеет 6 рёбер и по 4 грани и вершины. Если у тетраэдра все грани являются правильными треугольниками, то и сам тетраэдр называется правильным. Площадь полной поверхности любого многогранника, в том числе и тетраэдра можно рассчитать, зная площади его граней.

Инструкция

Чтобы найти площадь полной поверхности тетраэдра, необходимо вычислить площадь треугольника составляющего его грань.

Если треугольник равносторонний, то его площадь равна

S = √3 * 4 / a², где a – ребро тетраэдра,

тогда площадь поверхности тетраэдра находится по формуле

S = √3 * a².

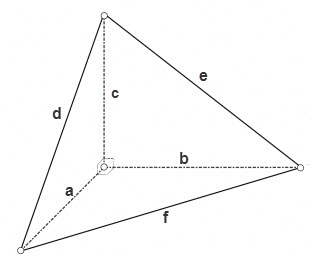
В случае, если тетраэдр является прямоугольным, т.е. все плоские углы при одной из его вершин являются прямыми, то площади трёх его граней являющихся прямоугольными треугольниками можно рассчитать по формуле

S = a * b *1/2,

S = a * c *1/2,

S = b * c *1/2,

площадь третьей грани можно рассчитать по одной из общих формул для треугольников, например по формуле Герона

S = √(p * (p – d) * (p – e) * (p – f)), где p = (d + e + f)/2 – полупериметр треугольника.

В общем случае, площадь любого тетраэдра можно рассчитать, используя формулу Герона для вычисления площадей каждой его грани.

Источники:

площадь поверхности тетраэдра
Найдите площадь сечения тетраэдра биссекторной плоскостью

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Найдите площадь сечения правильного тетраэдра PABC плоскостью, параллельной рёбрам PA и PC и проходящей через середину ребра PB, если все рёбра тетраэдра равны 8.

Найдите площадь сечения правильного тетраэдра PABC плоскостью, параллельной рёбрам PA и PC и проходящей через середину ребра PB, если все рёбра тетраэдра равны 4.

Аналоги к заданию № 488: 489 Все

Найдите площадь сечения правильного тетраэдра PABC плоскостью, проходящей через середины рёбер BC и PC параллельно ребру AC, если все рёбра тетраэдра равны 10.

Найдите площадь сечения правильного тетраэдра PABC плоскостью, проходящей через середины рёбер BC и PC параллельно ребру AC, если все рёбра тетраэдра равны 6.

Аналоги к заданию № 490: 491 Все

Найдите площадь сечения правильного тетраэдра PABC плоскостью, проходящей через точки, делящие рёбра PC и BC в отношении 2:1, считая от вершины C, параллельно ребру BP, если все рёбра тетраэдра равны 3.

Пройти тестирование по этим заданиям

Источник

Тема:

« Тетраэдр

и его сечение ».

Урок №2 10 класс стереометрия

10 класс

Актуализация опорных знаний

Вопросы:

1) Что такое многогранник? Какие многогранники вы знаете?

МНОГОГРАННИК – это поверхность геометрического тела, составленная из многоугольников.

Мы познакомимся с двумя из них – ТЕТРАЭДРОМ и ПАРАЛЛЕЛЕПИПЕДОМ.

Актуализация опорных знаний

2) Дайте определение тетраэдра.

Поверхность, составленная из четырех треугольников АВС , ADC, ADB и BDC , называется тетраэдром и обозначается: DABC .

Актуализация опорных знаний

3) Назовите элементы тетраэдра

Треугольники, из которых состоит тетраэдр, называются гранями.

ABC, ADC, ADB и BDC – грани тетраэдра DABC.

Стороны треугольников называются ребрами тетраэдра , а вершины треугольника – вершинами тетраэдра.

AB,AC,AD,DC,DB и BC – ребра,

A,B,C, и D – вершины тетраэдра.

Задача по готовому чертежу

Укажите все грани, ребра, вершины, противоположные ребра, скрещивающиеся ребра тетраэдра.

1) Определение секущей плоскости тетраэдра

Секущей плоскостью тетраэдра называют такую плоскость, по обе стороны от которой имеются точки тетраэдра.

Секущая плоскость пересекает грани тетраэдра по отрезкам .

Многоугольник, сторонами которого являются эти отрезки, называется сечением тетраэдра .

2) Сечение тетраэдра

Т.к. тетраэдр имеет четыре грани, то его сечениями могут быть только треугольники и четырёхугольники .

3) Правила построения сечений ТЕТРАЭДРА

а)Проводим прямые через точки, лежащие в одной плоскости;

б) Ищем прямые пересечения плоскости сечения с гранями многогранника, для этого:

— ищем точки пересечения прямой принадлежащей плоскости сечения с прямой, принадлежащей одной из граней (лежащие в одной плоскости);

— параллельные грани плоскость сечения пересекает по параллельным прямым.

Построение сечения тетраэдра через точки M, N, K

Построение:

1. KM

2. NM

Построение сечения тетраэдра через точки M, N, K

Построение:

3. NM ∩ АС = F

Построение сечения тетраэдра через точки M, N, K

Построение:

4. KF ∩ АС = L

5. KL

Построение сечения тетраэдра через точки M, N, K

Построение:

1. KM

2. NM

3. NM ∩ АС = F

4. KF ∩ АС = L

5. KL

6. LN

7. KLNM – искомое сечение

Объясните, как построить сечение тетраэдра DABC плоскостью, проходящей через точки M,N,K

Найдите периметр сечения, если

M, N, K – середины ребер и каждое ребро тетраэдра

равно а.

Объясните, как построить сечение тетраэдра DABC плоскостью, проходящей через точки M,N,K

Найдите периметр сечения, если M, N, K – середины ребер и каждое ребро тетраэдра равно а .

Индивидуальное задание

Построить сечение тетраэдра по данным точкам

Источник

Тетраэдр. Виды тетраэдров

Тетраэдр (четырёхгранник) — многогранник, гранями которого являются четыре треугольника (от греческого tetra — четыре и hedra — грань).

Рис. 1

У тетраэдра (4) грани, (4) вершины и (6) рёбер (Рис. 1).

Один из треугольников называется основанием тетраэдра, а три остальные — боковыми гранями тетраэдра.

В зависимости от видов треугольников и их расположения выделяют разные виды тетраэдров.

В школьном курсе чаще говорят о следующих видах тетраэдра:

– равногранный тетраэдр, у которого все грани — равные между собой треугольники;

– правильная треугольная пирамида — основание — равносторонний треугольник, все боковые грани — одинаковые равнобедренные треугольники (Рис. 3);

– правильный тетраэдр, у которого все четыре грани — равносторонние треугольники (Рис. 2).

Рис. 2 Рис. 3

Свойство правильного тетраэдра:

из определения правильного многогранника следует, что все рёбра тетраэдра имеют равную длину, а грани — равную площадь.

Параллелепипед. Виды параллелепипедов

Параллелепипедом называется многогранник, у которого (6) граней — параллелограммы.

Рис. 4

У параллелепипеда, как отмечено, (6) граней, (8) вершин и (12) рёбер (Рис. 4).

Две грани параллелепипеда, имеющие общее ребро, называются смежными, а не имеющие общих рёбер — противоположными.

Обычно выделяют какие-нибудь две противоположные грани и называют их основаниями, а остальные грани — боковыми гранями параллелепипеда.

Рёбра параллелепипеда, не принадлежащие основаниям, называют боковыми рёбрами.

Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю параллелепипеда (Рис. 5).

Рис. 5

В зависимости от видов параллелограммов и их расположения выделяют разные виды параллелепипедов:

параллелепипеды могут быть прямые и наклонные.

У прямых параллелепипедов боковые грани — прямоугольники (Рис. 5),

у наклонных — параллелограммы (Рис. 4).

Прямой параллелепипед, у которого основанием тоже является прямоугольник, называется прямоугольным параллелепипедом.

Рис. 6

Длины непараллельных рёбер прямоугольного параллелепипеда называются его линейными размерами (измерениями).

У прямоугольного параллелепипеда — три линейных размера:

DD1

(Рис. 6).

Свойства параллелепипеда:
– противоположные грани параллелепипеда равны и параллельны.

– Все четыре диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.

– Боковые грани прямого параллелепипеда — прямоугольники.

Построение сечения тетраэдра и параллелепипеда

Плоскостью сечения многогранника можно назвать любую плоскость, по обе стороны которой находятся точки многогранника.

Секущая плоскость пересекает грани многогранников по отрезкам.

Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника.

Так как у тетраэдра (4) грани, то сечением тетраэдра может быть треугольник (Рис. 7) или

четырёхугольник (Рис. 8).

Рис. 7 Рис. 8

У параллелепипеда (6) граней, поэтому сечением этого многогранника может быть треугольник (Рис. 9), четырёхугольник ( Рис. 10), пятиугольник (Рис. 11) или шестиугольник (Рис. 12).

При построении сечения надо вспомнить следующие знания из предыдущих тем:

1. если две точки прямой принадлежат плоскости, то прямая находится в этой плоскости.

2. Если две плоскости имеют общую точку, то эти плоскости пересекаются по прямой.

3. Если плоскость пересекает две параллельные плоскости, то линии пересечения параллельны.

Пример:

Задача

Построить сечение параллелепипеда плоскостью, которая проходит через точки (K), (M) и (N).