Как найти площадь трппеции

Как найти площадь трппеции

Выбирайте формулу в зависимости от известных величин.

1. Как найти площадь трапеции через основания и высоту

Посчитайте сумму оснований трапеции.

Умножьте результат на высоту и поделите на два.

Иллюстрация: Лайфхакер
  • S – искомая площадь трапеции.
  • a и b – основания трапеции (её параллельные стороны).
  • h – высота трапеции.

2. Как вычислить площадь трапеции через высоту и среднюю линию

Просто умножьте высоту трапеции на среднюю линию.

Иллюстрация: Лайфхакер
  • S – искомая площадь трапеции.
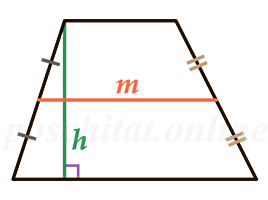
  • m – средняя линия трапеции (отрезок, соединяющий середины боковых сторон).
  • h – высота трапеции.

3. Как найти площадь трапеции через диагонали и угол между ними

Умножьте одну диагональ на другую, а затем — на синус любого угла между ними.

Поделите результат на два.

Иллюстрация: Лайфхакер
  • S – искомая площадь трапеции.
  • x и y – диагонали трапеции.
  • α – любой угол между диагоналями.

4. Как найти площадь трапеции через четыре стороны

Отнимите от большего основания меньшее.

Найдите квадрат полученного числа.

Прибавьте к результату квадрат одной боковой стороны и отнимите квадрат второй.

Поделите полученное число на удвоенную разность оснований.

Найдите квадрат результата и отнимите его от квадрата боковой стороны.

Найдите корень из полученного числа.

Умножьте результат на половину от суммы оснований.

Иллюстрация: Лайфхакер
  • S – искомая площадь трапеции.
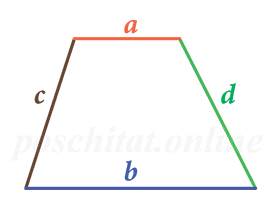
  • a, b – основания трапеции.
  • c, d – боковые стороны.

5. Как вычислить площадь равнобедренной трапеции через четыре стороны

Отнимите от большего основания трапеции меньшее и поделите результат на два.

Найдите квадрат полученного числа и отнимите его от квадрата боковой стороны.

Найдите корень из результата.

Умножьте полученное число на сумму оснований и поделите на два.

Иллюстрация: Лайфхакер
  • S — искомая площадь трапеции.
  • a, b — основания трапеции.
  • c, d — боковые стороны (напомним, в равнобедренной трапеции они равны).

6. Как найти площадь равнобедренной трапеции через радиус вписанной окружности и угол

Найдите квадрат радиуса и умножьте его на четыре.

Поделите результат на синус известного угла.

Иллюстрация: Лайфхакер
  • r — радиус вписанной окружности.
  • α — любой угол трапеции.

Читайте также 📐✏️🎓

  • 8 способов найти длину окружности
  • 8 способов найти периметр треугольника
  • 7 способов найти площадь прямоугольника
  • Как перевести обычную дробь в десятичную
  • Как освоить устный счёт школьникам и взрослым
Источник

Площадь трапеции

  1. Главная
  2. /
  3. Математика
  4. /
  5. Геометрия
  6. /
  7. Площадь трапеции

Чтобы найти площадь трапеции воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Через длины оснований и высоту

Площадь трапеции через длины оснований и высоту
Чему равна площадь трапеции, если:

основание a =
основание b =
высота h =

Ответ: S =

0

ед.²

Округление ответа:

Чему равна площадь трапеции если известны основания a и b, а также высота h?

Формула

S = ½ ⋅ (a + b) ⋅ h

Пример

Если у трапеции основание a = 3 см, основание b = 6 см, а высота h = 4 см, то её площадь:

S = ½ ⋅ (3 + 6) ⋅ 4 = 36 / 2 = 18 см²

Через среднюю линию и высоту

Площадь трапеции через среднюю линию и высоту
Чему равна площадь трапеции, если:

средняя линия m =
высота h =

Ответ: S =

0

ед.²

Округление ответа:

Чему равна площадь трапеции если известны средняя линия m и высота h?

Формула

S = m ⋅ h

Пример

Если у трапеции средняя линия m = 6 см, а высота h = 4 см, то её площадь:

S = 6 ⋅ 4 = 24 см²

Через длины сторон и оснований

Площадь трапеции через длины сторон и оснований
Чему равна площадь трапеции, если:

основание a =
основание b =
сторона c = сторона d =

Ответ: S =

0

ед.²

Округление ответа:

Чему равна площадь трапеции если известны основания a и b, а также стороны c и d?

Формула

Формула площади трапеции через длины сторон и оснований

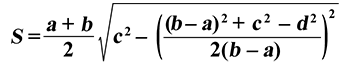
Пример

Если у трапеции основание a = 2 см, основание b = 6 см, сторона c = 4 см, а сторона d = 7 см, то её площадь:

S ≈ 13.555 см²

Через диагонали и угол между ними

Площадь трапеции через диагонали и угол между ними
Чему равна площадь трапеции, если:

диагональ d1 =
диагональ d2 =
угол α =

Ответ: S =

0

ед.²

Округление ответа:

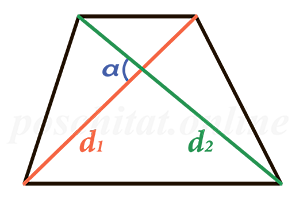
Чему равна площадь трапеции если известны диагонали d1 и d2 и угол между ними α?

Формула

S = ½ ⋅ d1 ⋅ d2 ⋅ sin(α)

Пример

Если у трапеции одна диагональ d1 = 5 см, другая диагональ d2 = 7 см, а угол между ними ∠α = 30°, то её площадь:

S = ½ ⋅ 5 ⋅ 7 ⋅ sin (30) = 17.5 ⋅ 0.5= 8.75 см²

Площадь равнобедренной трапеции

Через среднюю линию, боковую сторону и угол при основании

Площадь равнобедренной трапеции
Чему равна площадь трапеции, если:

средняя линия m =
сторона c =
угол α =

Ответ: S =

0

ед.²

Округление ответа:

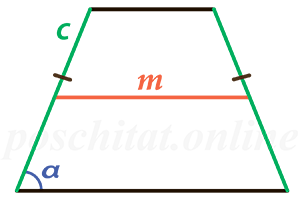
Чему равна площадь равнобедренной трапеции если средняя линия m, боковая сторона с, a угол при основании α?

Формула

S = m ⋅ c ⋅ sin(α)

Пример

Если у равнобедренной трапеции средняя линия m = 6 см, сторона c = 4 см, а угол при основании ∠α = 30°, то её площадь:

S = 6 ⋅ 4 ⋅ sin (30) = 24 ⋅ 0.5 = 12 см²

Через радиус вписанной окружности

Площадь равнобедренной трапеции через радиус вписанной окружности
Чему равна площадь трапеции, если:

радиус r =
угол α =

Ответ: S =

0

ед.²

Округление ответа:

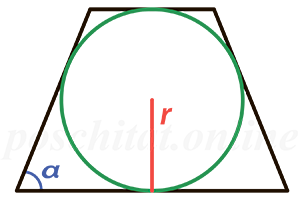
Чему равна площадь равнобедренной трапеции если радиус вписанной окружности r, a угол при основании α?

Формула

S = 4⋅r² ⁄ sin(α)

Пример

Если у равнобедренной трапеции радиус вписанной окружности r = 5 см, а угол при основании ∠α = 30°, то её площадь:

S = 4 ⋅ 5² / sin (30) = 100 / 0.5 = 200 см²

См. также

Источник

Как рассчитать площадь трапеции

На данной странице калькулятор поможет рассчитать площадь трапеции онлайн. Для расчета задайте высоту и длуну основания трапеции.

Трапеция – четырёхугольник, у которого две стороны параллельны (основания трапеции), а две другие – непараллельны (боковые стороны трапеции). Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.

Через основания и высоту

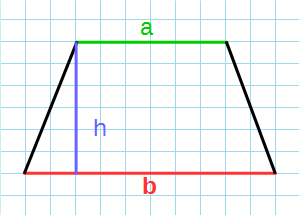
Трапеция с высотой и основаниями

Формула для нахождения площади трапеции через основания и высоту:

a,b – основания трапеции; h – высота трапеции.

Через среднюю линию и высоту

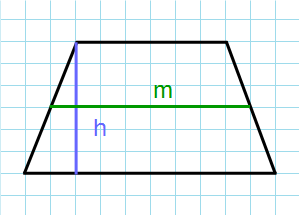
Трапеция с высотой и среденей линией

Формула для нахождения площади трапеции через основания и среднюю линию:

m – средняя линия; h – высота трапеции.

Через четыре стороны

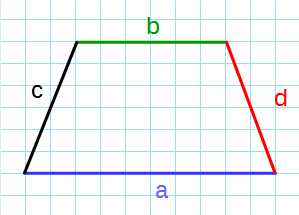
Трапеция с высотой и среденей линией

Формула для нахождения площади трапеции через основания и среднюю линию:

a – нижнее основание; b – верхнее основание; c, d – боковые стороны.

Через диагонали и угол между ними

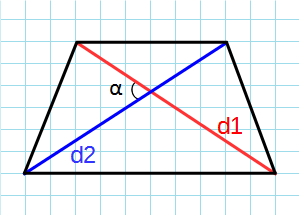
Трапеция с диагоналями

Формула для нахождения площади трапеции через диагонали и угол между ними:

d1, d2 – диагонали трапеции; α – угол между диагоналями.

Через среднюю линию, боковую сторону и угол при основаниии

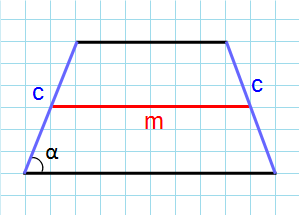
Трапеция со средней линией и боковой стороной

Формула для нахождения площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании:

m – средняя линия трапеции; c – боковая сторона трапеции; α – угол при основании.

Через радиус вписанной окружности

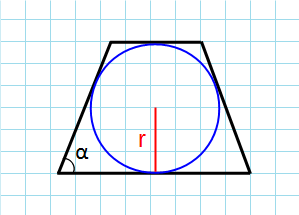
Трапеция с вписанной окружностью

Формула для нахождения площади равнобедренной трапеции через радиус вписанной оккужности:

r – радиус окружности; α – угол при основании.

Источник


Загрузить PDF


Загрузить PDF

Трапеция является четырехугольником, у которого две параллельные стороны (основания) имеют разную длину. Формула для вычисления площади трапеции: S = ½(b1+b2)h, где b1 и b2 — основания, h — высота трапеции. Если известны только боковые стороны правильной трапеции, ее можно разбить на ряд простых фигур, чтобы найти высоту, а затем вычислить площадь.

  1. Изображение с названием Calculate the Area of a Trapezoid Step 1

    1

    Сложите основания. Основания — это две стороны трапеции, которые параллельны друг другу. Если значения оснований не даны, измерьте их линейкой, а затем сложите полученные значения.[1]

    • Например, если верхнее основание (b1) равно 8 см, а нижнее (b2) — 13 см, сумма оснований b = b1 + b2 = 8 + 13 = 21 см.

  2. Изображение с названием Calculate the Area of a Trapezoid Step 2

    2

    Измерьте высоту трапеции. Высота трапеции — это расстояние между параллельными основаниями. Проведите перпендикуляр к основаниям, а затем с помощью линейки измерьте его и запишите найденное значение.[2]

    • Помните, что высота не равна боковым сторонам трапеции. Высота равна боковой стороне трапеции, только если эта сторона перпендикулярна основаниям.

  3. Изображение с названием Calculate the Area of a Trapezoid Step 3

    3

    Перемножьте сумму оснований и высоту. То есть умножьте значение «b» на значение «h». Результат запишите в квадратных единицах измерения.[3]

    • В нашем примере: 21 x 8 = 147 см2.

  4. Изображение с названием Calculate the Area of a Trapezoid Step 4

    4

    Разделите найденное значение на 2, чтобы найти площадь трапеции. Также найденное значение можно умножить на ½. Результат запишите в квадратных единицах измерения.[4]

    • В нашем примере: S = 147/2 = 73,5 см2.

    Реклама

  1. Изображение с названием Calculate the Area of a Trapezoid Step 5

    1

    Разбейте трапецию на 1 прямоугольник и 2 прямоугольных треугольника. Проведите два перпендикуляра из вершин трапеции на нижнее основание. Так вы получите 1 прямоугольник (посередине) и 2 прямоугольных равных треугольника (по бокам).[5]

    • Этот метод можно применить только к правильной трапеции.

  2. Изображение с названием Calculate the Area of a Trapezoid Step 6

    2

    Найдите основание прямоугольного треугольника. Для этого сначала вычтите верхнее основание из нижнего основания. Теперь найденное значение разделите на 2, чтобы вычислить основание треугольника. На данном этапе вам известны основание и гипотенуза треугольника.[6]

    • Например, если верхнее основание (b1) трапеции равно 6 см, а нижнее основание (b2) равно 12 см, основание треугольника равно 3 см (потому что b = (b2 – b1)/2 = (12 – 6)/2 = 3 см).

  3. Изображение с названием Calculate the Area of a Trapezoid Step 7

    3

    Найдите высоту трапеции по теореме Пифагора. Для этого подставьте значения основания и гипотенузы треугольника в формулу A2 + B2 = C2, где A — основание, C — гипотенуза. Найдите значение B, то есть высоту трапеции. Если основание треугольника равно 3 см, а гипотенуза равна 5 см:[7]

    • Подставьте значения: 32 + B2 = 52
    • Возведите в квадрат: 9 + B2 = 25
    • Вычтите 9 из каждой стороны уравнения: B2 = 16
    • Извлеките квадратный корень из каждой стороны уравнения: B = 4 см

    Подсказка: если в уравнении нет идеального квадрата, упростите ответ и оставьте квадратный корень. Например, √32 = √(16)(2) = 4√2.

  4. Изображение с названием Calculate the Area of a Trapezoid Step 8

    4

    Подставьте значения оснований и высоты в формулу для вычисления площади трапеции. Формула: S = ½(b1 + b2)h. Результат запишите в квадратных единицах измерения.[8]

    • Запишите формулу: S = ½(b1 + b2)h
    • Подставьте значения: S = (6 + 12)(4)
    • Упростите выражение и перемножьте числа: S = ½(18)(4)
    • Ответ: S = 36 см2.

    Реклама

Советы

  • Если вам известна медиана трапеции (отрезок, который соединяет середины боковых сторон трапеции и параллелен основаниям трапеции), умножьте ее на высоту, чтобы найти площадь.[9]

Реклама

Об этой статье

Эту страницу просматривали 105 334 раза.

Была ли эта статья полезной?

Источник

Трапеция – это геометрическая фигура; четырехугольник, имеющий 2 параллельные и 2 непараллельные стороны.

  • Формулы вычисления площади

    • По длине оснований и высоте

    • Через длины всех сторон (Формула Герона)

    • Через диагонали и угол между ними

  • Примеры задач

Формулы вычисления площади

По длине оснований и высоте

Площадь трапеции (S) равняется половине суммы ее оснований, умноженной на высоту, проведенную к ним.

Формула расчета площади трапеции по основаниям и высоте

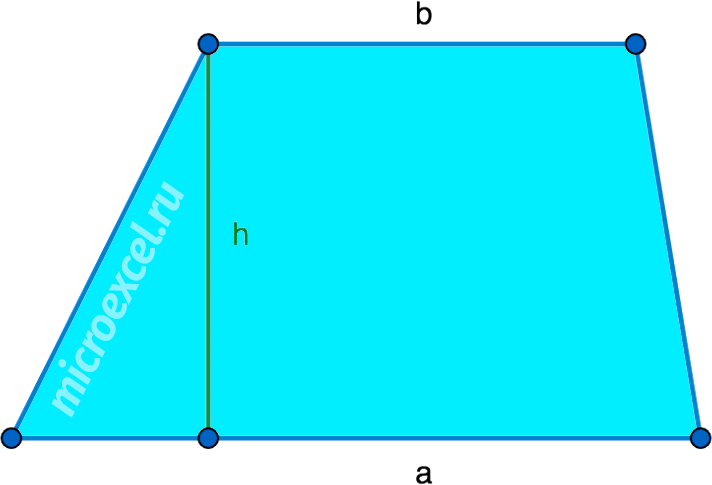
Расчет площади трапеции по основаниям и высоте

Через длины всех сторон (Формула Герона)

Для вычисления площади трапеции необходимо знать длины всех ее сторон:

Формула расчета площади трапеции через длины всех ее сторон

Расчет площади трапеции через длину всех ее сторон

p – полупериметр трапеции, считается по формуле:

Формула расчета полупериметра трапеции

Через диагонали и угол между ними

Площадь трапеции равна половине произведения диагоналей и синуса угла между ними. Вычисляется по одной из двух формул ниже:

Формула расчета площади трапеции через диагонали и угол между ними

Формула расчета площади трапеции через диагонали и угол между ними

Расчет площади трапеции по диагоналям и углу между ними

Примеры задач

Задание 1
Найдите площадь трапеции, если ее основания равны 4 и 7 см, а высота – 4 см.

Решение:
Используем первую формулу, рассмотренную выше: S = 1/2 * (4 см + 7 см) * 4 см = 22 см2.

Задание 2
Найдите площадь трапеции, если ее основания равны 6 и 12 см, а боковые стороны – 8 и 10 см.

Решение:
Т.к. нам известны длины всех сторон, применим формулу Герона:
S = (6+12) / |6-12| * √(18-6)(18-12)(18-6-8)(18-6-10) = 18 / 6 * √576 = 72 см2.

Источник

Добавить комментарий