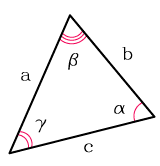
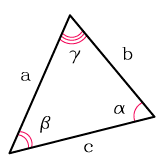
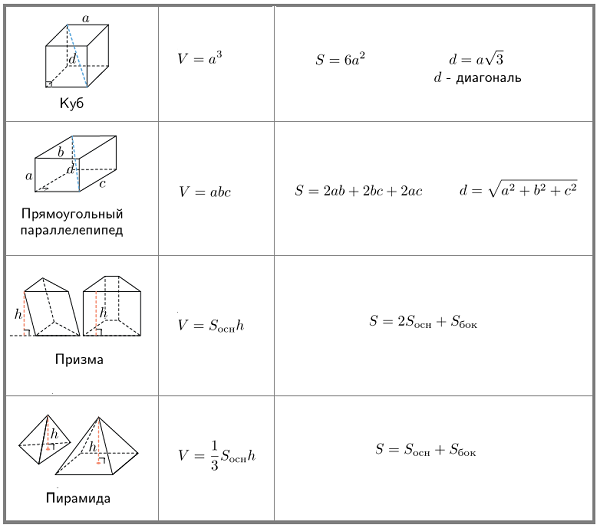
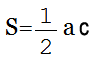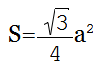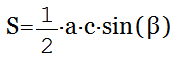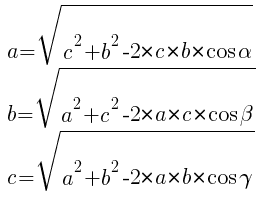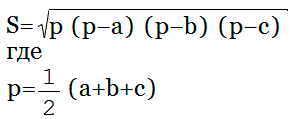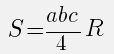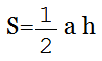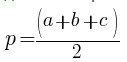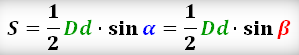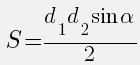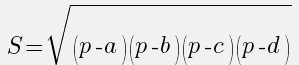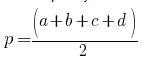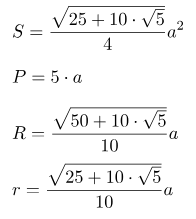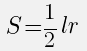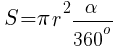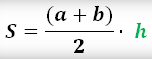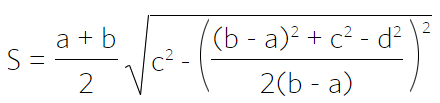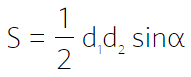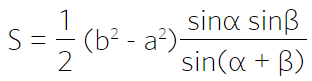Формула расчета площади треугольника
Треугольник это плоская фигура, которая имеет три стороны и три угла. Сумма всех трех углов, равна 180 градусов.
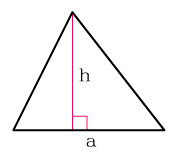
Высота треугольника это – опущенный перпендикуляр из вершины угла на противоположенную сторону или ее продолжение, которую в этом случае, называют основанием.
Что бы найти площадь треугольника,
для этого надо основание умножить на высоту и разделить на два
1. Площадь разностороннего треугольника
h – высота треугольника
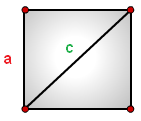
Формула площади треугольника (S):
Калькулятор для расчета площади треугольника
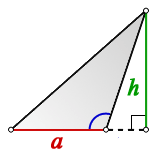
2. Площадь треугольника с тупым углом
h – высота треугольника
Формула площади треугольника с тупым углом (S):
Формулы для треугольника:
Тупоугольный треугольник
Что такое тупоугольный треугольник
Тупоугольный треугольник — геометрическая фигура на плоскости, которая представляет собой треугольник, один из углов которого является тупым, то есть больше 90º.
Такой треугольник не может быть прямоугольным и равносторонним, но может быть равнобедренным.
Сумма углов треугольника равна 180º. Именно поэтому только один из них может быть больше 90º, два других всегда острые. Это единственная особенность данной фигуры. Подход к решению задач с такой фигурой не отличается от решения задач с треугольниками других типов.
Элементы тупоугольного треугольника
Помимо сторон и углов, тупоугольный треугольник имеет следующие элементы:
- Внешний угол — тот, который смежен с внутренним, всего их шесть, по два на один внутренний. Внешний угол тупого всегда будет острым, острого — тупым.
- Медиана — отрезок, который соединяет вершину треугольника с противолежащей стороной и делит ее пополам. Все медианы пересекаются друг с другом в одной точке (центроиде). Эта точка делит медианы в соотношении 2:1, считая от вершины.
- Высота — перпендикуляр, который проведен из высоты треугольника на противоположную сторону. В тупоугольном треугольнике может лежать за пределами фигуры.
- Биссектриса — прямая, делящая угол пополам. Делит противоположную сторону на отрезки, которые пропорциональны прилежащим сторонам фигуры. Точка, которая является пересечением биссектрис, также является центром вписанной окружности.
Формулы площади тупоугольного треугольника
Для нахождения площади, периметра и других показателей тупоугольного треугольника используются те же формулы, что и для вычисления любого произвольного треугольника.
Площадь данной фигуры можно найти при помощи следующих формул:
S = ½ * x * h , где х — сторона;
S = √ p * ( p – x ) * ( p – y ) * ( p – z ) ,
p — полупериметр, p = ( x + y + z ) / 2
S = x * y * z / 4 * R , R — радиус описанной окружности;
S = p * r , p — полупериметр, r — радиус вписанной окружности.
Пример решения задачи
Найти площадь тупоугольного треугольника, у которого стороны равны x=9, y=5, z=6.
Для решения задачи стоит использовать формулу площади с полупериметром.
p = ( x + y + z ) / 2 , p = ( 9 + 5 + 6 ) / 2 = 20 / 2 = 10 .
S = √ p * ( p – x ) * ( p – y ) * ( p – z ) , S = √ 10 * ( 10 – 9 ) * ( 10 – 5 ) * ( 10 – 6 ) = √ 10 * 1 * 5 * 4 = √ 200 = 10 √ 2
Как найти площадь треугольника
О чем эта статья:
8 класс, 9 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
Площадь — это численная характеристика, которая дает нам информацию о размере части плоскости, ограниченной замкнутой геометрической фигурой.
Если значения заданы в разных единицах измерения длины, мы не сможем узнать, какая площадь треугольника получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
Популярные единицы измерения площади:
- квадратный миллиметр (мм 2 );
- квадратный сантиметр (см 2 );
- квадратный дециметр (дм 2 );
- квадратный метр (м 2 );
- квадратный километр (км 2 );
- гектар (га).
Формула площади треугольника
Для решения задач применяются различные формулы, в зависимости от известных исходных данных. Далее мы рассмотрим способы решения для всех типов треугольников, в том числе частные случаи для равносторонних, равнобедренных и прямоугольных фигур.
Быстро вычислить площадь треугольника поможет наш онлайн-калькулятор. Просто введите известные вам значения и получите ответ в метрах, сантиметрах или миллиметрах.
Научиться быстро щелкать задачки на нахождение площади треугольника помогут курсы по математике от Skysmart!
Общая формула
1. Площадь треугольника через основание и высоту
, где — основание, — высота.
2. Площадь треугольника через две стороны и угол между ними
, где , — стороны, — угол между ними.
3. Площадь треугольника через описанную окружность и стороны
, где , , — стороны, — радиус описанной окружности.
4. Площадь треугольника через вписанную окружность и стороны
, где , , — стороны, — радиус вписанной окружности.
Если учитывать, что — это способ поиска полупериметра, то формулу можно записать следующим образом:
5. Площадь треугольника по стороне и двум прилежащим углам
, где — сторона, и — прилежащие углы.
6. Формула Герона для вычисления площади треугольника
Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.
, где , , — стороны, — полупериметр, который можно найти по формуле:
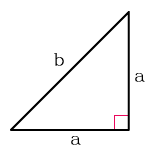
Для прямоугольного треугольника
Площадь треугольника с углом 90° по двум сторонам
Площадь треугольника по гипотенузе и острому углу
, где — гипотенуза, — любой из прилегающих острых углов.
Гипотенузой принято называть сторону, которая лежит напротив прямого угла.
Площадь прямоугольного треугольника по катету и прилежащему углу
, где — катет, — прилежащий угол.
Катетом принято называть одну из двух сторон, образующих прямой угол.
Площадь треугольника через гипотенузу и радиус вписанной окружности
, где — гипотенуза, — радиус вписанной окружности.
Площадь треугольника по отрезкам, на которые делит вписанная окружность его гипотенузу
, где , — части гипотенузы.
Площадь прямоугольного треугольника по формуле Герона
, где , — катеты, — полупериметр, который можно найти по формуле:
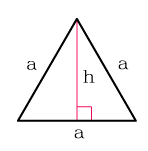
Для равнобедренного треугольника
Вычисление площади через основание и высоту
, где — основание, — высота, проведенная к основанию.
Поиск площади через боковые стороны и угол между ними
, где — боковая сторона, — угол между боковыми сторонами.
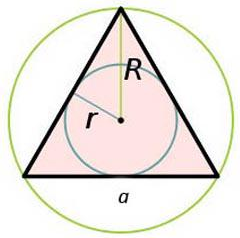
Площадь равностороннего треугольника через радиус описанной окружности
, где — радиус описанной окружности.
Площадь равностороннего треугольника через радиус вписанной окружности
, где — радиус вписанной окружности.
Площадь равностороннего треугольника через сторону
Площадь равностороннего треугольника через высоту
Таблица формул нахождения площади треугольника
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу, использовать как закладку в тетрадке или учебнике и обращаться к ней по необходимости.
[spoiler title=”источники:”]
http://wika.tutoronline.ru/geometriya/class/7/tupougolnyj-treugolnik
http://skysmart.ru/articles/mathematic/ploshad-treugolnika
[/spoiler]
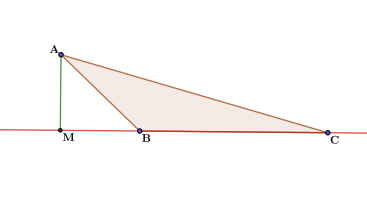
В тупоугольном треугольнике высота, проведённая из вершины острого угла, лежит вне треугольника.
Вот об этом часто забывают школьники и пытаются вместить высоту внутрь треугольника по подобию медианы и биссектрисы, которые всегда лежат внутри треугольника.
А высота в общем случае – это перпендикуляр, опущенный из вершины основания на прямую, содержащую противоположную сторону. На отрезок из точки перпендикуляр опустить не всегда можно, а на прямую – всегда. Поэтому нужно сторону треугольника продлить до прямой, а потом уже опустить на неё перпендикуляр из вершины. Длина этого перпендикуляра – это и есть высота, проведённая к этой стороне (точнее, из вершины угла, лежащего против этой стороны). Длину этой стороны a нужно умножить на эту высоту h и разделить пополам. Получится площадь для тупоугольного треугольника:
А если высота проведена из вершины тупого угла, к самой длинной стороне, то в этом случае она лежит внутри треугольника, и площадь уже вычисляется по привычной формуле – полупроизведение основания на высоту, проведённую к основанию. Здесь уже основанием служит самая длинная сторона, та, которая лежит против тупого угла. А в предыдущем случае она была одной из двух коротких сторон, прилегающих к тупому углу. Любую сторону треугольника можно выбрать основанием, но если основание выбрано, то под высотой следует понимать высоту, проведённую к основанию, т. е. длину перпендикуляра, опущенного на прямую, содержащую основание, из вершины, лежащей против основания.
Есть и множество других формул для площади треугольника, как тупоугольного, так и любого другого, но все они так или иначе выводятся из этой.
Если пользоваться формулой для площади треугольника через стороны треугольника и угол между ними (S = (1/2)*b*c*sin α), то надо помнить, что синус тупого угла равен синусу острого угла, дополняющего этот тупой угол до 180 градусов. Это послужило одной из причин, чтобы расширить понятия синуса и косинуса, определяемых в прямоугольном треугольнике, в котором нет тупого угла, обобщив эти понятия на любой угол, который может встретиться в треугольнике.
В остальном особенности формул для площади тупоугольного треугольника такие же, как и для любого треугольника. В зависимости от данных, пригодна та или иная формула. Универсальная формула Герона, к примеру (S² = p*(p-a)*(p-b)*(p-c), где p = (a+b+c) / 2 – полупериметр треугольника), требует только знания трёх сторон треугольника, вне зависимости от того, какой это треугольник – тупоугольный, остроугольный или прямоугольный.
Тупоугольный треугольник

4.6
Средняя оценка: 4.6
Всего получено оценок: 145.
4.6
Средняя оценка: 4.6
Всего получено оценок: 145.
Тупоугольный треугольник мало чем отличается от обычных произвольных остроугольных треугольников, но тупой угол делает треугольник непривычным для восприятия. Это зачастую приводит в недоумение, поэтому стоит рассмотреть различные варианты решения задач на нахождение параметров тупоугольного треугольника.
Опыт работы учителем математики – более 33 лет.
Определения
Тупоугольным треугольником будет называться любой треугольник, содержащий тупой угол. Тупоугольный треугольник может быть равнобедренным, но при этом не может быть равносторонним или прямоугольным. Собственно на этом свойства этой фигуры заканчиваются. В остальном, это обычный треугольник и подход к решению таких фигур ничем не отличается.
В треугольнике сумма углов равна 180 градусам, поэтому только один угол треугольника может быть тупым, два других при этом всегда острые. Площадь тупоугольного треугольника находится так же, как площадь произвольного треугольника.
Только в тупоугольном треугольнике высота может лежать за пределами треугольника.
Рассмотрим несколько интересных задач на нахождение данных в тупоугольном треугольнике.
Пример решения задачи
В тупоугольном треугольнике АВС известно, что косинус тупого угла равен $-2/sqrt{13}$. Сторона АС находится напротив тупого угла, $АВ=sqrt{13}$, ВС=2. Необходимо найти внешнюю высоту треугольника АМ.
Для решения любой задачи можно найти несколько способов. В данной ситуации можно пойти через площадь треугольников, достроить тупоугольный треугольник до прямоугольного или воспользоваться теоремой косинусов. Каждый из способов дает представление о том, как можно решать задачи с тупоугольным треугольником. Воспользуемся каждым из них.
Ответ в каждом случае должен быть одинаков. Но если округлять неточные ответы, то в одной задаче при одинаковых решениях можно получить разные величины. Будьте внимательны, результат не должен отличаться больше, чем на 1.
- Через площадь треугольников. Площадь можно найти как половину произведения основания на высоту, проведенную к этому основанию. А можно – как половину произведения двух сторон на синус угла между ними. Нам известен косинус угла, а через косинус всегда можно найти синус.
$$sin(ABC)=sqrt{1-cos^2(ABC)}=sqrt{13-4 over13}=sqrt{9 over13}={3oversqrt{13}}$$
Теперь запишем две формулы площади, выразим через них высоту и найдем ее значение.
$$S={1over2}*AM*BC$$
$$S={1over2}*AB*BC sin(ABC)$$
$${1over2}*AM*BC={1over2}*AB*BC*sin(ABC)$$
$$AM*ВС=AB*BC*sin(ABC)$$
$$AM=AB*sin(ABC)$$
$$AM=sqrt{13}*{3 over sqrt{13}}=3$$
- Второй способ – это достроить тупоугольный треугольник до прямоугольного. Если присмотреться, то можно заметить на чертеже два прямоугольных треугольника – это треугольники АМС и АМВ. В треугольнике АМВ можно найти косинус угла АВМ с помощью формул-приведений. Затем, через значение косинуса найти значение синуса того же угла. А синус – это отношение противолежащего катета к гипотенузе. Противолежащей катет – это искомая нами высота, а гипотенуза – это сторона АВ прямоугольного треугольника.
$$cos(ABM)=cos(180-ABC)=-cos(ABC)$$
$$cos(ABM)=-cos(ABC)={2over sqrt{13}}$$
Тогда синус, как и в первом способе, выразим через основное тригонометрическое тождество.
$$Sin(ABM)=sqrt{1-cos(ABM)^2}=sqrt{13-4over13}=sqrt{9over13}={3oversqrt{13}}$$
$$Sin(ABM)=AM/AB$$
$$AM=AB*sin(ABM)=sqrt{13}*{3oversqrt{13}}=3$$
- Третий метод – это теорема синусов и косинусов. Для того, чтобы воспользоваться этим способом, через теорему косинусов найдем значение АС, потом через теорему синусов найдем синус угла АСВ и определим АМ из синуса угла АСВ большого прямоугольного треугольника АМС.
$$АС=sqrt{AB^2+BC^2-2AB*BC*cos(ABC)}=$$
$$sqrt {sqrt{13}^2+2^2-2*sqrt{13}*{-2oversqrt{13}}}=$$
$$sqrt{13+4+8}=sqrt{25}=5$$ – по теореме косинусов.
$${АСover{sin(ABC)}}={ABover{sin(ACB)}}$$ – по теореме синусов.
Значение синуса угла АВС определим по основному тригонометрическому тождеству.
$$ Sin(ABC)=sqrt{1-cos^2(ABC)}=sqrt{13-{4over{4}}}=sqrt{9over{13}}={3oversqrt{13}}$$
Выразим искомый синус угла АСВ.
$$Sin(ACB)=AB*{sin(ABC)over{AC}}$$
$$Sin(ACB)=(sqrt{13}*{{3oversqrt{13}}over{5}})={3over5}$$
Выразим из треугольника АМС и найденного значения синуса сторону АМ.
$$Sin(ACB)={AMover AC}$$
$$AM=sin(ACB)*AC$$
$$AM={3over5}*{5}=3$$
Ответы всех трех способов совпали, а, значит, задача решена верно.
Что мы узнали?
Мы поговорили об определении тупоугольного треугольника. Узнали и посмотрели на практике, какие методы решения тупоугольных треугольников существуют, а также выяснили ,какие формулы и теоремы необходимо знать для успешного решения тупоугольного треугольника.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-
Азамат Дильдабаев
5/5
-
Арина Алисултанова
5/5
-
Иван Дарьин
5/5
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 145.
А какая ваша оценка?
Как найти площадь любого треугольника
Вспоминаем геометрию: формулы для произвольных, прямоугольных, равнобедренных и равносторонних фигур.
Как найти площадь любого треугольника
Посчитать площадь треугольника можно разными способами. Выбирайте формулу в зависимости от известных вам величин.
Зная сторону и высоту
- Умножьте сторону треугольника на высоту, проведённую к этой стороне.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a — сторона треугольника.
- h — высота треугольника. Это перпендикуляр, опущенный на сторону или её продолжение из противоположной вершины.
Зная две стороны и угол между ними
- Посчитайте произведение двух известных сторон треугольника.
- Найдите синус угла между выбранными сторонами.
- Перемножьте полученные числа.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a и b — стороны треугольника.
- α — угол между сторонами a и b.
Зная три стороны (формула Герона)
- Посчитайте разности полупериметра треугольника и каждой из его сторон.
- Найдите произведение полученных чисел.
- Умножьте результат на полупериметр.
- Найдите корень из полученного числа.
- S — искомая площадь треугольника.
- a, b, c — стороны треугольника.
- p — полупериметр (равен половине от суммы всех сторон треугольника).
Зная три стороны и радиус описанной окружности
- Найдите произведение всех сторон треугольника.
- Поделите результат на четыре радиуса окружности, описанной вокруг прямоугольника.
- S — искомая площадь треугольника.
- R — радиус описанной окружности.
- a, b, c — стороны треугольника.
Зная радиус вписанной окружности и полупериметр
Умножьте радиус окружности, вписанной в треугольник, на полупериметр.
- S — искомая площадь треугольника.
- r — радиус вписанной окружности.
- p — полупериметр треугольника (равен половине от суммы всех сторон).
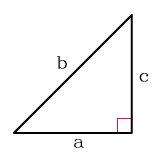
Как найти площадь прямоугольного треугольника
- Посчитайте произведение катетов треугольника.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a, b — катеты треугольника, то есть стороны, которые пересекаются под прямым углом.
Как найти площадь равнобедренного треугольника
- Умножьте основание на высоту треугольника.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a — основание треугольника. Это та сторона, которая не равняется двум другим. Напомним, в равнобедренном треугольнике две из трёх сторон имеют одинаковую длину.
- h — высота треугольника. Это перпендикуляр, опущенный на основание из противоположной вершины.
Как найти площадь равностороннего треугольника
- Умножьте квадрат стороны треугольника на корень из трёх.
- Поделите результат на четыре.
- S — искомая площадь треугольника.
- a — сторона треугольника. Напомним, в равностороннем треугольнике все стороны имеют одинаковую длину.
Читайте также 🧠👨🏻🎓✍🏻
- 7 причин полюбить математику
- ТЕСТ: Помните ли вы геометрию?
- 10 хитрых головоломок со спичками для тренировки воображения
- Интересные математические факты для тех, кто хочет больше узнать о мире вокруг
- ТЕСТ: Сможете ли вы решить простые математические примеры?
Содержание:
- Площадь треугольника
- Площадь параллелограмма
- Формула площади прямоугольника
- Площадь квадрата
- Площадь четырехугольника
- Площадь многоугольника
- Площадь ромба
- Площадь многогранника
- Площадь пятиугольника
- Площадь закрашенного сектора
- Площадь круга
- Площадь трапеции
Площадь треугольника
Прямоугольного
Равностороннего треугольника
Площадь равнобедренного прямоугольного треугольника
S = a2/2
Площадь треугольника через синус
Площадь треугольника через косинус
Для нахождения площади треугольника нужно знать все стороны. По теореме косинусов квадрат неизвестной стороны равен:
Следовательно:
Далее используем формулу Герона:
Площадь треугольника через радиус описанной окружности
Произвольного треугольника
Формула Герона
Площадь треугольника через высоту
Площадь треугольника через полупериметр
Формула Герона
является полупериметром.
Площадь тупоугольного треугольника
S = ah/2
Площадь треугольника через радиус вписанной окружности
S = p×r
где p – полупериметр:
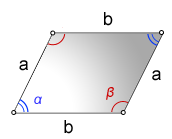
Площадь параллелограмма
Через синус
Через стороны и углы
S = a×b×sin(α) = a×b×sin(β)
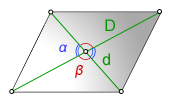
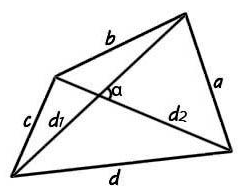
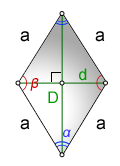
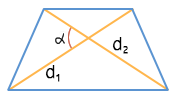
Через диагонали и угол между ними
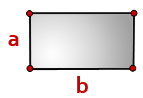
Формула площади прямоугольника
S = a×b
Площадь квадрата
S = a2
Площадь четырехугольника
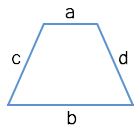
Выпуклого четырехугольника
где
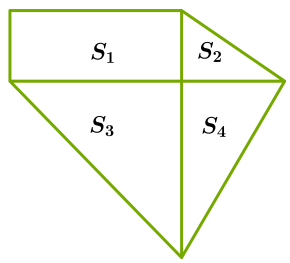
Площадь многоугольника
S = S1 + S2 + S3 + S4
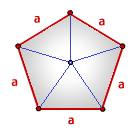
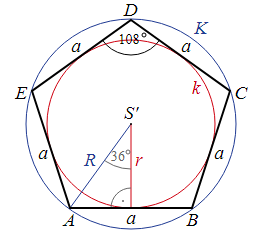
Правильного многоугольника
где n – количество сторон многоугольника.
Площадь ромба
Площадь многогранника
Площадь пятиугольника
Площадь закрашенного сектора
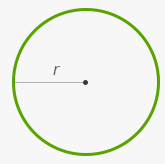
Площадь круга
S = πr2
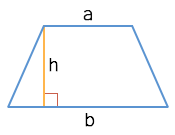
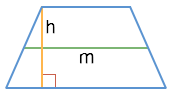
Площадь трапеции
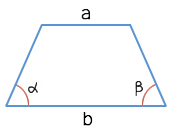
Через основания и высоту
Через высоту и среднюю линию
S = hm
Через четыре стороны
Через диагонали и угол между ними
Через основания и два угла