Наверно, даже тот, кто в школе был отъявленным троечником, ответит на этот вопрос утвердительно. И в самом деле – формула проста и легко запоминается: нужно лишь длину основания умножить на длину опущенного до этого основания из противолежащего угла перпендикуляра (высоты), и затем разделить на два. С прямоугольным треугольником – вообще красота: перемножай длины катетов – и половина от полученного произведения как раз и будет площадью фигуры.
Ответ почти на «пятерку»! Ну а прочему – «почти»? Потому что это не единственный способ, а зачастую – и весьма труднореализуемый.


Мнение эксперта:
Афанасьев Е.В.
Главный редактор проекта Stroyday.ru.
Инженер.
Задать вопрос эксперту
Например, при работе на местности, в условиях, когда треугольник – явно не прямоугольный, а без специального геодезического инструмента сложно отбить точный перпендикуляр. Вы полностью уверены, что знаете, как рассчитывается площадь треугольника в таких условиях? Нет ли какого-нибудь метода, что позволял бы избежать дополнительных построений или вычерчиваний схем в масштабе? Скажем, можно было бы обойтись только промером длин сторон с помощью рулетки?
Да, такой метод тоже существует, вот только помнят о нем не все. По все видимости потому что лежащая в его основе формула Герона — довольно-таки «тяжеловесная», не располагающая к быстрому и четкому запоминанию.
Рассчитываем площадь треугольника по формуле Герона
Многим может показаться, что расчет площади треугольника – вообще мало кому нужное занятие. Ведь на практике при строительстве, проведении ремонта, при работах на территории участка чаще приходится иметь дело с четырёхугольниками.
Возможно, это и так, но треугольник тоже очень часто может пригодиться.
- Ну, во-первых, не надо делать категоричных заключений. Нечасто, но встречаются и треугольные территории. А если говорить о разбивке этой территории на зоны, особенно при использовании радиального принципа, то есть от центра по расходящимся к периферии лучам – треугольников может получиться больше чем достаточно. Нельзя совсем исключить треугольники и в области архитектуры — тому тоже немало примеров.

- А во-вторых, и это главное, знание этого вопроса поможет вам «бороться» и с куда более сложными фигурами. Ведь любой многоугольник, независимо от количества его вершин, можно воображаемыми секущими линиями разбить на совокупность прилегающих друг к другу треугольников различной формы и размеров.

И если знать формулу вычисления площади только по длине сторон, то не придется делать каких-то дополнительных построений. То есть меряй себе рулеткой расстояния от точки до точки – и считай!
Правда, формула одним своим видом быстро развеивает оптимизм:
Формула Герона:
S = √ (p × (p – а) × (p – b) × (p – c))
S — площадь треугольника;
a b c — длины сторон треугольника;
p — полупериметр треугольника, то есть
p = (a + b + c) / 2
М-да,, так просто, в уме – и не подсчитаешь, Тем более что в формуле присутствует еще и квадратный корень…
А в уме и не надо – это очень точно и быстро сделает за вас онлайн-калькулятор, размещенный ниже.
Калькулятор расчета площади треугольного участка
Перейти к расчётам
Тот редкий случай, когда никаких пояснений по расчету, должно быть, и не требуется. Знай себе, подставляй промеренные длины сторон – и получай готовый результат.
А как быть с остальными фигурами?
С многоугольными – понятно. А если присутствуют ещё и округлые формы? Приходится разбираться с каждым случаем индивидуально, и очень часто для этого отыскивается то или иное приемлемое решение. Разбор интересных с точки зрения геометрии вариантов проведен в специальной статье нашего портала, посвященной именно расчету площадей.
Наверно, даже тот, кто в школе был отъявленным троечником, ответит на этот вопрос утвердительно. И в самом деле – формула проста и легко запоминается: нужно лишь длину основания умножить на длину опущенного до этого основания из противолежащего угла перпендикуляра (высоты), и затем разделить на два. С прямоугольным треугольником – вообще красота: переможай длины катетов – и половина от полученного произведения как раз и будет плоадью фигуры.
Ответ почти на «пятерку»! Ну а прочему – «почти»? Потому что это не единственный способ, а зачастую – и весьма труднореализуемый.

Да, такой метод тоже существует, вот только помнят о нем не все. По все видимости потому что лежащая в его основе формула Герона — довольно-таки «тяжеловесная», не располагающая к быстрому и четкому запоминанию.
Рассчитываем площадь треугольника по формуле Герона
Многим может показаться, что расчет площади треугольника – вообще мало кому нужное занятие. Ведь на практике при строительстве, проведении ремонта, при работах на территории участка чаще приходится иметь дело с четырёхугольниками.
Возможно, это и так, но треугольник тоже очень часто может пригодиться.
- Ну, во-первых, не надо делать категоричных заключений. Нечасто, но встречаются и треугольные территории. А если говорить о разбивке этой территории на зоны, особенно при использовании радиального принципа, то есть от центра по расходящимся к периферии лучам – треугольников может получиться больше чем достаточно. Нельзя совсем исключить треугольники и в области архитектуры — тому тоже немало примеров.

- А во-вторых, и это главное, знание этого вопроса поможет вам «бороться» и с куда более сложными фигурами. Ведь любой многоугольник, независимо от количества его вершин, можно воображаемыми секущими линиями разбить на совокупность прилегающих друг к другу треугольников различной формы и размеров.

И если знать формулу вычисления площади только по длине сторон, то не придется делать каких-то дополнительных построений. То есть меряй себе рулеткой расстояния от точки до точки – и считай!
Правда, формула одним своим видом быстро развеивает оптимизм:
Формула Герона:
S = √ (p × (p – а) × (p – b) × (p – c))
S — площадь треугольника;
a b c — длины сторон треугольника;
p — полупериметр треугольника, то есть
p = (a + b + c) / 2
М-да,, так просто, в уме – и не подсчитаешь, Тем более что в формуле присутствует еще и квадратный корень…
А в уме и не надо – это очень точно и быстро сделает за вас онлайн-калькулятор, размещенный ниже.
Калькулятор расчета площади треугольного участка
Перейти к расчётам
Тот редкий случай, когда никаких пояснений по расчету, должно быть, и не требуется. Знай себе, подставляй промеренные длины сторон – и получай готовый результат.
А как быть с остальными фигурами?
С многоугольными – понятно. А если присутствуют ещё и округлые формы? Приходится разбираться с каждым случаем индивидуально, и очень часто для этого отыскивается то или иное приемлемое решение. Разбор интересных с точки зрения геометрии варинтов проведен в специальной статье нашего портала, посвященной именно расчету площадей.
Данный калькулятор поможет Вам вычислить площадь земельного участка, даже если участок имеет не строго прямоугольную форму,
а представляет собой многоугольник с непрямыми углами. Вычисления производятся методом треугольников. Этот метод основан на двух постулатах:
1) Любой многоугольник можно разбить на треугольники (см. схемы разбивки ниже)

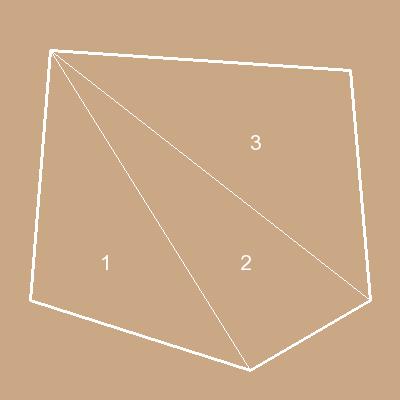


2) Зная длины сторон треугольника, его площадь можно вычислить по формуле Герона
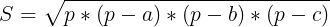
где
a, b, c – длины сторон треугольника
p – полупериметр треугольника, вычисляемый по формуле
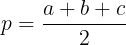
Таким образом, чтобы узнать площадь земельного участка, нужно разбить участок на треугольники и замерить длины сторон всех треугольников.
После этого занести результаты замера в калькулятор. Или самим вычислить поочередно площадь каждого треугольника по вышеприведенным формулам, а
потом площади всех треугольников сложить.
Примечание: если Вам известны координаты поворотных точек Вашего участка, то можно рассчитать площадь,
воспользовавшись формулой немецкого математика и геодезиста Иоганна Карла Фридриха Гаусса (формулой землемера)
Калькулятор площади участка
Замер участка можно производить с помощью бечевки или шпагата. Главное, чтобы бечевка не была эластичной. А если Вам не обязательно нужен точный результат
(достаточно и приблизительного), то можно воспользоваться более быстрым и менее трудозатратным способом – измерять длины сторон шагами.
Шаг среднего человека равен приблизительно одному аршину (71,12 см). Замерьте расстояние шагами, а в калькуляторе укажите единицы измерения – аршины.
Выбор калькулятора для расчета земельно участка, зависит от его формы: прямоугольный, ромбический, круглый, треугольный, неправильной формы, четырехсторонний с разными сторонами.
Расчет площади участка квадратной или прямоугольной формы
Проще всего рассчитать площадь участка прямоугольной формы. Для этого нужно знать только его длину и ширину.
Площадь треугольного участка, четырехугольного с разными сторонами, пятиугольного

Расчет участка круглой формы
Для расчета площади участка круглой формы, воспользуйтесь онлайн-калькулятором вычисления площади круга. Для расчетов нужно знать лишь диаметр круга.
Площадь – важнейшая характеристика участка, которая может быть необходима при различных сделках. Например, при продаже, покупке или обмене участка. Этот показатель обязательно присутствует в перечне параметров участка, зафиксированных в ЕГРН.
СодержаниеПоказать
- Виды расчета площади
- Аналитический расчет
- Треугольная форма
- Четырехугольная форма
- Многоугольная форма
Виды расчета площади
Существуют следующие виды расчета площади:
- аналитический;
- графический;
- механический.
Аналитический метод наиболее точен, поскольку его точность зависит только от точности полевых измерений. В двух других методах дополнительные ошибки могут появиться еще и из-за неточности планов и деформации бумаги.
В первом случае при расчете используются результаты полевых измерений координат или длин границ участка, во втором случае используются данные, полученные с плана участка, в третьем случае используется специальный прибор – планиметр.
Аналитический расчет
Наиболее полный и точный расчет можно произвести по координатам поворотных точек. Такие координаты определяются кадастровым инженером при проведении межевания участка. Вычисление таких координат производится с помощью различных методов, указанных в приказе МЭР № 518 «О требованиях в точности определения характерных точек».
Наиболее точными методами определения координат являются геодезический и спутниковый методы, для которых используются опорные межевые сети. Эти координаты можно получить в выписке из ЕГРН.
При этом площадь участка вычисляется по формуле Гаусса:
S=0,5*(x1-1+ x2y3+…+ xn-1yn+ xny1- x2y1- x3y2-…- xnyn-1- x1yn),

где xi, yi –координаты i-той опорной точки.
Для проведения такого сложного расчета надо знать координаты опорных точек земельного участка.
На практике часто требуется оценить площадь земельного участка на месте. При этом в качестве средства измерения может быть только рулетка.
В этом случае порядок расчета площади зависит от геометрической формы участка. Для простой формы участка площадь считается в соответствии с простейшими правилами геометрии.
Треугольная форма
Например, площадь участка в виде прямоугольного треугольника рассчитывается по формуле:
S=0,5*a*b,
где а и b – длина двух сторон участка.
Для треугольника, не являющимся прямоугольным, площадь равна:
S=0,5*h*b,
где b – основание фигуры, а h – его высота.
На практике не всегда удается измерить высоту треугольника, отображающего форму участка. Проще измерить длины сторон. В этом случае для расчета площади участка используется формула Герона:
S=√(p-a)*(p-b)*(p-c),
где а,b и c – стороны треугольника, а p=0,5*(a+b+c) – полупериметр треугольника.
Четырехугольная форма
Для участка в виде прямоугольника площадь равна:
S=a*b,
где а и b – размеры длинной и короткой сторон прямоугольника.
Для участка в форме трапеции площадь равна:
S= (a+b)/2*h,

где а и b – длины оснований фигуры, а h – ее высота.
В общем случае площадь участка в виде четырехугольника можно определить по формуле:
S=0,5*d1*d2*sin α,
где d1и d2 – диагонали фигуры, а α – угол между ними.
В некоторых случаях площадь четырехугольного участка можно вычислить по его четырем сторонам. В частности, если четырехугольник, отображающий форму участка, может быть вписан в окружность (то есть суммы его противоположных углов равны между собой и равны 180°), то его площадь вычисляется по формуле Брахмагупты, подобной формуле Герона для треугольника:
S=√(p-a)*(p-b)*(p-c)*(p-d),
где а,b,c и d – стороны четырехугольника, а p=0,5*(a+b+c+d) – его полупериметр.
Многоугольная форма
Для участка со сложным контуром основной прием расчета его площади состоит в разбиении сложной фигуры на простые (например, треугольники и прямоугольники). Вычисленные площади простых фигур затем суммируются.
Возможный алгоритм действий для определения площади участка, имеющего форму многоугольника, состоит в следующем:

- Выбрать точку внутри многоугольника и забить в нее колышек.
- От колышка к каждой вершине многоугольника протянуть бечевку.
- С помощью рулетки измерить длины каждой из сторон всех образовавшихся треугольников.
- По формуле Герона вычислить площади треугольников.
- Просуммировав площади треугольников, получить величину площади участка.
Если многоугольник не имеет внутренних углов, больших 180 градусов, центральную точку можно совместить с одной из вершин. В этом случае количество образовавшихся треугольников уменьшится на 2, что упростит задачу.
В некоторых случаях, когда участок имеет слишком сложную форму и много опорных точек, более правильным приемом является использование замеров по азимуту. При этом для каждой опорной точки по контуру границы участка определяется размер угла по азимуту и расстояние до следующей опорной точки. Измерения производятся по часовой стрелке. После окончания измерений все результаты загружаются в специальную программу, которая с большой точностью рассчитывает площадь участка.
