Как рассчитать площадь трапеции
На данной странице калькулятор поможет рассчитать площадь трапеции онлайн. Для расчета задайте высоту и длуну основания трапеции.
Трапеция – четырёхугольник, у которого две стороны параллельны (основания трапеции), а две другие – непараллельны (боковые стороны трапеции). Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
Через основания и высоту
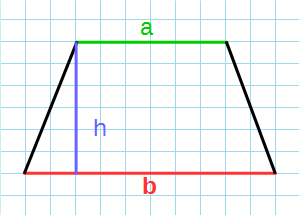
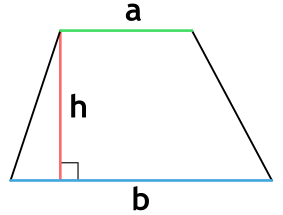
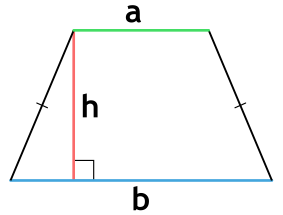
Формула для нахождения площади трапеции через основания и высоту:
a,b – основания трапеции; h – высота трапеции.
Через среднюю линию и высоту
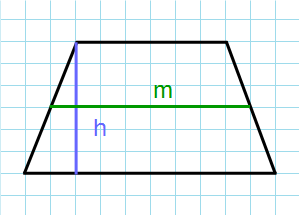
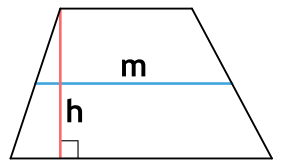
Формула для нахождения площади трапеции через основания и среднюю линию:
m – средняя линия; h – высота трапеции.
Через четыре стороны
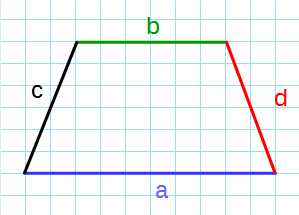
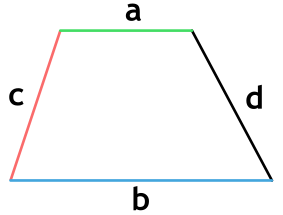
Формула для нахождения площади трапеции через основания и среднюю линию:
a – нижнее основание; b – верхнее основание; c, d – боковые стороны.
Через диагонали и угол между ними
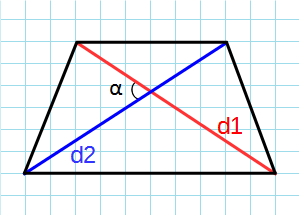
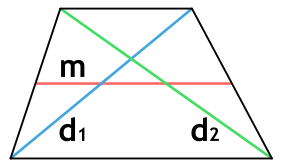
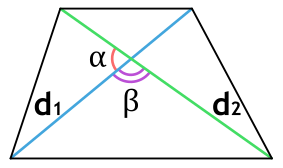
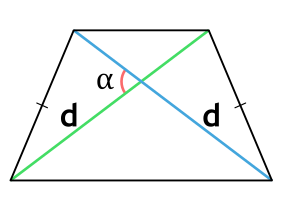
Формула для нахождения площади трапеции через диагонали и угол между ними:
d1, d2 – диагонали трапеции; α – угол между диагоналями.
Через среднюю линию, боковую сторону и угол при основаниии
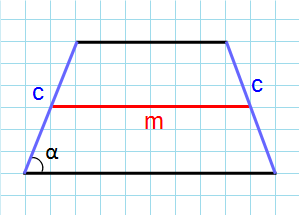
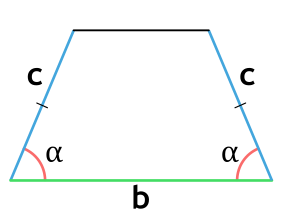
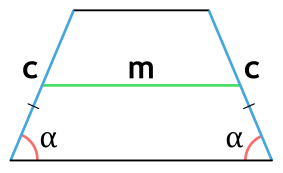
Формула для нахождения площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании:
m – средняя линия трапеции; c – боковая сторона трапеции; α – угол при основании.
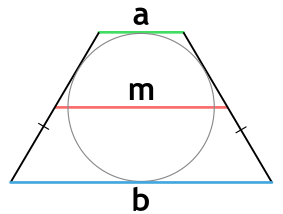
Через радиус вписанной окружности
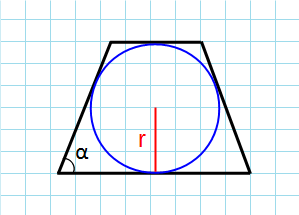
Формула для нахождения площади равнобедренной трапеции через радиус вписанной оккужности:
r – радиус окружности; α – угол при основании.

{S = dfrac{1}{2} (a + b) cdot h}
Площадь трапеции можно найти множеством способов. Для вас мы собрали все возможные варианты нахождения площади. Для вашего удобства для каждой формулы создан калькулятор, который поможет рассчитать площадь трапеции по известным данным. От вас требуется только подставить значения и в режиме онлайн мгновенно получить ответ. Формулы и калькуляторы сгруппированы по типам трапеций – обычная, равнобедренная (равнобокая).
- Калькулятор площади трапеции
- Площадь трапеции
- через основания и высоту
- через среднюю линию и высоту
- через диагонали и среднюю линию
- через 4 стороны
- через диагонали и угол между ними
- через основания и углы при основании
- через площади треугольников
- через диагонали и высоту
- через радиус вписанной окружности и основания
- через перпендикулярные диагонали
- Площадь равнобедренной (равнобокой) трапеции
- через основания и высоту
- через 3 стороны (формула Брахмагупты)
- через верхнее основание, боковую сторону и угол при нижнем основании
- через нижнее основание, боковую сторону и угол при нижнем основании
- через основания и угол
- через диагонали и угол между ними
- через боковую сторону, угол при основании и среднюю линию
- через радиус вписанной окружности и угол при основании
- Площадь равнобедренной (равнобокой) трапеции, в которую можно вписать окружность
- через высоту (диаметр вписанной окружности) и угол при основании
- через основания и угол при основании
- через основания и радиус вписанной окружности
- через основания
- через основания и боковую сторону
- через основания и среднюю линию
- Примеры задач
Площадь трапеции
Трапеция — выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Площадь трапеции через основания и высоту
{S = dfrac{1}{2} (a + b) cdot h}
a и b – основания трапеции
h – высота, проведенная к основанию
Площадь трапеции через среднюю линию и высоту
{S = m cdot h}
m – средняя линия трапеции
h – высота трапеции
Площадь трапеции через диагонали и среднюю линию
{S = sqrt{p(p-d_1)(p-d_2)(p-2m)}}
{p = dfrac{d_1+d_2+2m}{2}}
d1 и d2 – диагонали трапеции
m – средняя линия трапеции
Площадь трапеции через 4 стороны
{S = dfrac{a+b}{2} sqrt{c^2 – {Big( dfrac{(a-b)^2 + c^2 – d^2}{2(a-b)} Big)}^2}}
a, b, c и d – стороны трапеции
Площадь трапеции через диагонали и угол между ними
{S = dfrac{d_1 cdot d_2}{2}cdot sin(alpha); S = dfrac{d_1 cdot d_2}{2}cdot sin(beta)}
d1 и d2 – диагонали трапеции
α или β – угол между диагоналями трапеции
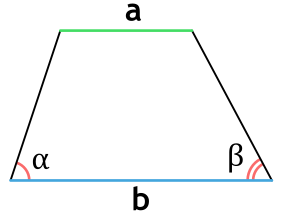
Площадь трапеции через основания и углы при основании
{S = dfrac{b^2 – a^2}{2} cdot dfrac{sin(alpha) cdot sin(beta)}{sin(alpha + beta)}}
a и b – основания трапеции
α или β – прилежащие к основанию трапеции углы
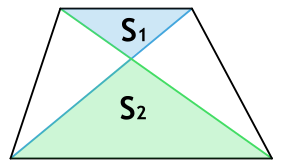
Площадь трапеции через площади треугольников
{S = (sqrt{S_1} + sqrt{S_2})^2}
S1 и S2 – площади образованных пересечением диагоналей трапеции треугольников
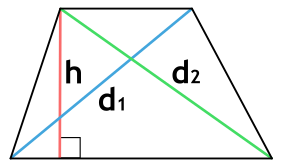
Площадь трапеции через диагонали и высоту
{S = dfrac{sqrt{{d_2}^2-h^2}+sqrt{{d_1}^2-h^2}}{2} cdot h}
d1 и d2 – диагонали трапеции
h – высота трапеции
Площадь трапеции через радиус вписанной окружности и основания
{S = (a+b)cdot r}
a и b – основания трапеции
r – радиус вписанной в трапецию окружности
Площадь трапеции через перпендикулярные диагонали
{S = dfrac{1}{2} cdot d_1 cdot d_2}
d1 и d2 – перпендикулярные диагонали трапеции
Площадь равнобедренной (равнобокой) трапеции
Равнобедренная трапеция — это трапеция, у которой боковые стороны равны.
Площадь равнобедренной трапеции через основания и высоту
{S = dfrac{a+b}{2} cdot h}
a и b – основания равнобедренной трапеции
h – высота, проведенная к основанию равнобедренной трапеции
Площадь равнобедренной трапеции через 3 стороны (формула Брахмагупты)
{S = sqrt{(p-a)(p-b)(p-c)^2}}
{p = dfrac{a+b+2c}{2}}
a и b – основания равнобедренной трапеции
c – боковая сторона равнобедренной трапеции
Площадь равнобедренной трапеции через верхнее основание, боковую сторону и угол при нижнем основании
{S = c cdot sin(alpha) cdot (a+c cdot cos(alpha))}
a – верхнее основание равнобедренной трапеции
c – боковая сторона равнобедренной трапеции
α – прилежащие к нижнему основанию трапеции углы
Площадь равнобедренной трапеции через нижнее основание, боковую сторону и угол при нижнем основании
{S = c cdot sin(alpha) cdot (b-c cdot cos(alpha))}
b – нижнее основание равнобедренной трапеции
c – боковая сторона равнобедренной трапеции
α – прилежащий к нижнему основанию трапеции угол
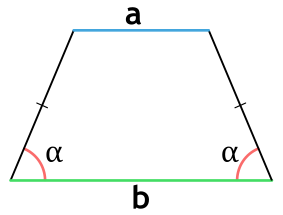
Площадь равнобедренной трапеции через основания и угол
{S = dfrac{1}{2}(b^2-a^2) cdot tg(alpha)}
a и b – основания равнобедренной трапеции
α – прилежащий к основанию трапеции угол
Площадь равнобедренной трапеции через диагонали и угол между ними
{S = dfrac{1}{2}d^2 cdot sin(alpha)}
a – диагональ равнобедренной трапеции
α – угол между диагоналями равнобедренной трапеции
Площадь равнобедренной трапеции через боковую сторону, угол при основании и среднюю линию
{S = m cdot c cdot sin(alpha)}
m – средняя линия равнобедренной трапеции
c – боковая сторона равнобедренной трапеции
α – угол при основании равнобедренной трапеции
Площадь равнобедренной трапеции через радиус вписанной окружности и угол при основании
{S = dfrac{4r^2}{sin(alpha)}}
r – радиус вписанной окружности
α – угол при основании равнобедренной трапеции
Площадь равнобедренной (равнобокой) трапеции, в которую можно вписать окружность
В трапецию можно вписать окружность тогда и только тогда, когда суммы ее противоположных сторон равны.
Площадь равнобедренной трапеции, в которую можно вписать окружность, через высоту (диаметр вписанной окружности) и угол при основании
{S = dfrac{h^2}{sin(alpha)}}
h – высота равнобедренной трапеции
α – угол при основании равнобедренной трапеции
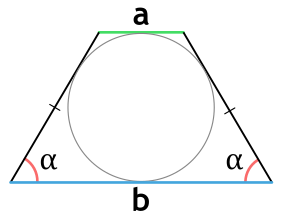
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и угол при основании
{S = dfrac{a cdot b}{sin(alpha)}}
a и b – основания равнобедренной трапеции
α – угол при основании равнобедренной трапеции
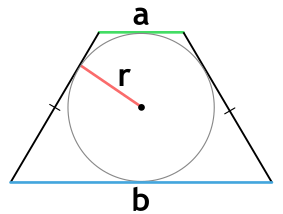
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и радиус вписанной окружности
{S = r(a+b); r=dfrac{sqrt{a cdot b}}{2}}
a и b – основания равнобедренной трапеции
r – радиус вписанной окружности
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания
{S = sqrt{a cdot b} cdot dfrac{a+b}{2}}
a и b – основания равнобедренной трапеции
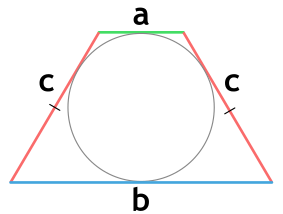
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и боковую сторону
{S = c cdot sqrt{a cdot b}}
a и b – основания равнобедренной трапеции
c – боковая сторона равнобедренной трапеции
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и среднюю линию
{S = m cdot sqrt{a cdot b}}
a и b – основания равнобедренной трапеции
m – средняя линия равнобедренной трапеции
Примеры задач на нахождение площади трапеции
Задача 1
Найдите площадь трапеции, если основания равны 6см и 9 см, а высота трапеции равна 5 см.
Решение
Для решения задачи воспользуемся первой формулой.
S = dfrac{1}{2} (a + b) cdot h = dfrac{1}{2} (6 + 9) cdot 5 = dfrac{1}{2} cdot 15 cdot 5 = dfrac{1}{2} cdot 75 = 37dfrac{1}{2} : см^2
Ответ: 37.5 см²
Полученный ответ легко проверить с помощью калькулятора .
Задача 2
Найдите площадь трапеции средняя линия которой равна 18 см, а высота 9 см.
Решение
С решением этой задачи нам поможет вторая формула.
S = m cdot h = 18 cdot 9 = 162 : см^2
Ответ: 162 см²
Воспользуемся калькулятором для проверки результата.
Задача 3
Найдите площадь трапеции диагонали которой равны 10 и 8, а средняя линия равна 3.
Решение
Для решения этой задачи нам поможет третья формула.
На первом этапе вычислим p:
p = dfrac{d_1+d_2+2m}{2} = dfrac{10+8+2 cdot 3}{2} = dfrac{10+8+6}{2} = dfrac{24}{2} = 12
А теперь можно вычислить площадь трапеции:
S = sqrt{p(p-d_1)(p-d_2)(p-2m)} = sqrt{12(12-10)(12-8)(12-2 cdot 3)} = sqrt{12 cdot 2 cdot 4 cdot 6} = sqrt{576} = 24 : см^2
Ответ: 24 см²
Осталось проверить полученный ответ.
Задача 4
Найдите площадь трапеции диагонали которой равны 17 и 15, а средняя линия равна 4.
Решение
Задача похожа на ту, что мы только что решили. Поэтому повторим шаги.
На первом этапе вычислим p:
p = dfrac{d_1+d_2+2m}{2} = dfrac{17+15+ 2 cdot 4}{2} = dfrac{17+15+8}{2} = dfrac{40}{2} = 20
А теперь можно вычислить площадь трапеции:
S = sqrt{p(p-d_1)(p-d_2)(p-2m)} = sqrt{20(20-17)(20-15)(20-2 cdot 4)} = sqrt{20 cdot 3 cdot 5 cdot 12} = sqrt{3600} = 60 : см^2
Ответ: 60 см²
Проверка .
Задача 5
Найдите площадь трапеции диагонали которой равны 8 и 6 а средняя линия равна 5.
Решение
Еще одна типовая задача. Повторим действия как в задачах выше.
На первом этапе вычислим p:
p = dfrac{d_1+d_2+2m}{2} = dfrac{8+6+ 2 cdot 5}{2} = dfrac{8+6+10}{2} = dfrac{24}{2} = 12
А теперь можно вычислить площадь трапеции:
S = sqrt{p(p-d_1)(p-d_2)(p-2m)} = sqrt{12(12-8)(12-6)(12-2 cdot 5)} = sqrt{12 cdot 4 cdot 6 cdot 2} = sqrt{576} = 24 : см^2
Ответ: 24 см²
Проверка .
Задача 6
Найдите площадь равнобедренной трапеции если её основания равны 5 см и 17 см, а боковая сторона равна 10 см.
Решение
Для решения этой задачи используем формулу Брахмагупты.
Сначала вычислим p:
p = dfrac{a+b+2c}{2} = dfrac{5+17+2 cdot 10}{2} = dfrac{22+20}{2} = dfrac{42}{2} = 21
А теперь можно вычислить площадь трапеции:
S = sqrt{(p-a)(p-b)(p-c)^2} = sqrt{(21-5)(21-17)(21-10)^2} = sqrt{16 cdot 4 cdot 11^2} = sqrt{16 cdot 4 cdot 121} = sqrt{7744}= 88 : см^2
Ответ: 88 см²
Проверка .
Задача 7
Острый угол равнобедренной трапеции равен 45°, а основания равны 8 и 6 см. Найдите площадь трапеции.
Решение
Для решения этой задачи воспользуемся формулой.
S = dfrac{1}{2}(b^2-a^2) cdot tg(alpha) = dfrac{1}{2}(8^2-6^2) cdot tg(45°)
Тангенс 45° = 1, продолжим вычисления:
S = dfrac{1}{2}(8^2-6^2) cdot tg(45°) = dfrac{1}{2}(64-36) cdot 1 = dfrac{1}{2} cdot 28 = 14 : см^2
Ответ: 14 см²
Убедиться в правильности решения нам поможет калькулятор .
Трапеция, ее свойства, формулы площади, высоты, сторон.
Трапеция – это выпуклый четырехугольник, у которого только одна пара сторон параллельна.
Трапеция (понятие, определение)
Видеоурок “Трапеция”
Виды трапеций
Элементы трапеции: основания, боковые стороны, средняя линия и высота
Свойства трапеции
Свойства равнобедренной трапеции
Формулы трапеции
Трапеция (понятие, определение):
Трапеция (от др.-греч. τραπέζιον – «столик» от τράπεζα – «стол») – это выпуклый четырёхугольник, у которого две стороны параллельны, а другие две стороны не параллельны.
Трапеция – это выпуклый четырехугольник, у которого только одна пара сторон параллельна.
Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, и стороны не равны между собой.
Рис. 1. Трапеция
Выпуклым четырёхугольником называется четырёхугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
@ https://youtu.be/Q4EpXexoMrM
Виды трапеций:
Равнобедренная трапеция или равнобокая трапеция – это трапеция, у которой боковые стороны равны.
Рис. 2. Равнобедренная трапеция
Прямоугольная трапеция – это трапеция, один из углов при боковой стороне которой прямой.
Прямоугольная трапеция – это трапеция, имеющая прямые углы при боковой стороне.
Рис. 3. Прямоугольная трапеция
Элементы трапеции: основания, боковые стороны, средняя линия и высота:
Параллельные стороны трапеции называются основаниями трапеции, а две другие – непараллельные – боковыми сторонами.
Рис. 4. Трапеция
AD и BC – основания трапеции, AB и CD – боковые стороны трапеции.
AD – большее основание трапеции, BC – меньшее основание трапеции.
Отрезок, соединяющий середины боковых сторон трапеции, называется средняя линия.
Рис. 5. Трапеция и срединная линия
Расстояние между основаниями трапеции называется высотой трапеции.
Рис. 6. Трапеция
Высота трапеции (h) определяется формулой:
где b – большее основание трапеции, a – меньшее основание трапеции, c и d – боковые стороны трапеции.
Свойства трапеции:
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
Рис. 7. Трапеция и срединная линия
MN || BC, MN || AD,
l = (a + b) / 2
2. Отрезок, соединяющий середины диагоналей трапеции, равен половине разности оснований и лежит на средней линии.
Рис. 8. Трапеция
MN = (b – a) / 2
3. Сумма внутренних углов трапеции (и любого другого четырёхугольника) равна 360° .
Сумма углов, прилежащих к боковой стороне трапеции, равна 180° .
Рис. 9. Трапеция
4. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
Рис. 9. Трапеция
5. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.

AB = BK
6. Если сумма углов при одном из оснований трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
Рис. 11. Трапеция
∠BAD + ∠CDA = 90°, MN = (AD – DC) / 2
7. В трапецию можно вписать окружность, если сумма длин оснований трапеции равна сумме длин её боковых сторон.
Рис. 12. Трапеция
AB + CD = AD + BC
В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.
Рис. 13. Трапеция
Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований).
Рис. 14. Трапеция
MN = (AB + CD) / 2,
MN = (AD + BC) / 2
8. Диагонали трапеции делят ее на 4 треугольника.
Два из них, прилежащие к основаниям, подобны.
Два других, прилежащие к боковым сторонам, имеют одинаковую площадь.
Рис. 15. Трапеция
Треугольники BCO и AOD подобны. Коэффициент подобия треугольников (k) находится как отношение оснований трапеции. k = AD / BC. Отношение площадей этих подобных треугольников есть k2.
Треугольники ABO и CDO имеют одинаковую площадь.
9. Каждая диагональ в точке пересечения делится на две части с таким соотношением длины, как соотношение между основаниями.
Рис. 16. Трапеция
BC : AD = OC : AO = OB : DO
10. Диагонали трапеции d1 и d2 связаны со сторонами соотношением:
d12 + d22 = 2ab + c 2 + d 2
где b – большее основание трапеции, a – меньшее основание трапеции, c и d – боковые стороны трапеции.
11. Средняя линия трапеции разделяет пополам любой отрезок, который соединяет основания трапеции, так же делит диагонали пополам.
Рис. 17. Трапеция
AK = KB, AM = MC, BN = ND, CL = LD,
KL – средняя линия
Рис. 17. Трапеция
AK = KB, AM = MC, BN = ND, CL = LD,
KL – средняя линия, UV – отрезок, который соединяет основания трапеции
12. Средняя линия разбивает трапецию на две трапеции, площади которых соотносятся как:
где b – большее основание трапеции, a – меньшее основание трапеции, S1 и S2 – площади образованных трапеций, в результате разделения средней линией.
Рис. 18. Трапеция
S1 – площадь трапеции MBCN,
S2 – площадь трапеции AMND
Свойства равнобедренной трапеции:
1. Прямая, которая проходит через середины оснований, перпендикулярна основаниям, тем самым, является осью симметрии равнобедренной трапеции.
2. Высота, опущенная из вершины на большее основание равнобедренной трапеции, делит его на два отрезка, один из которых равен полусумме оснований, а другой — полуразности оснований.
3. Углы при любом основании равнобедренной трапеции равны.
4. Сумма противоположных углов равнобедренной трапеции равна 180°.
5. Длины диагоналей равнобедренной трапеции равны.
6. Вокруг равнобедренной трапеции можно описать окружность.
7. При перпендикулярности диагоналей в равнобедренной трапеции ее высота равна полусумме оснований.
Формулы трапеции:
Пусть a – большее основание трапеции, b – меньшее основание трапеции, c – левая сторона трапеции, d – правая сторона трапеции, α и β – углы при нижнем основании трапеции, d1 и d2 – диагонали трапеции, m – средняя линия трапеции, h – высота трапеции, γ и δ – углы между диагоналями трапеции, S – площадь трапеции, P – периметр трапеции.
Формулы для определения сторон трапеции:
Через среднюю линию и одно из оснований трапеции:
a = 2m – b
b = 2m – a
Через высоту и углы при нижнем основании трапеции:
a = b + h · (ctg α + ctg β)
b = a – h · (ctg α + ctg β)
Через боковые стороны и углы при нижнем основании:
a = b + c·cos α + d·cos β
b = a – c·cos α – d·cos β
Через высоту и углы при нижнем основании трапеции:
Формулы для определения средней линии трапеции:
Через длины оснований трапеции:
Через площадь и высоту трапеции:
Формулы для определения высоты трапеции:
Через сторону и прилегающий угол при нижнем основании трапеции:
h = c·sin α = d·sin β
Через диагонали трапеции и углы между ними:
Через диагонали трапеции, углы между ними и среднюю линию трапеции:
Через площадь и длины оснований трапеции:
Через площадь и длину средней линии трапеции:
Формула для определения периметра трапеции:
P = a + b + c + d
Формулы для определения площади трапеции:
Через основания и высоту трапеции:
Через среднюю линию и высоту трапеции:
S = m · h
Через диагонали трапеции и угол между ними:
Через все стороны трапеции:
С помощью формулы Герона для трапеции:
Как называется объемная трапеция?
Если трапецию изобразить в объеме, то такая фигура будет напоминать усеченную пирамиду.
В правильной усеченной пирамиде боковые грани являются равнобокими трапециями.
Квадрат
Овал
Полукруг
Прямой угол
Прямоугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Ромб
Трапеция
Тупой угол
Шестиугольник
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Видео https://youtu.be/Q4EpXexoMrM
Коэффициент востребованности
6 463
Трапеция — это четырехугольник, в котором две противоположные стороны параллельны.
Онлайн-калькулятор площади трапеции
Введем некоторые понятия, которые в дальнейшем помогут решить задачи, связанные с нахождением площади данной фигуры.
Основания трапеции — это стороны, параллельные друг другу.
Боковые стороны — соответственно, две оставшиеся стороны.
Средняя линия — отрезок, который соединяет центры боковых сторон. Эта линия всегда параллельна основаниям трапеции.
Виды трапеций
Трапеция бывает трех видов:
- Равнобедренная – та, у которой боковые стороны равны.
- Прямоугольная, у которой два углы прямые, т. е. равны 90 градусам.
- Произвольная, которая не относится к двум вышеописанным категориям.
Площадь трапеции можно найти различными способами. Разберем их более подробно и закрепим материал решением простых задач.
Формула площади трапеции по основанию и высоте
Пусть нам дана произвольная трапеция. Чтобы найти ее площадь, воспользуемся следующей формулой:
S=a+b2⋅hS=frac{a+b}{2}cdot h
a,ba, b — основания трапеции;
hh — высота трапеции.
Найти площадь SS трапеции, в которой известны основания, численно равные 10 (см.) и 8 (см.) и высота, длиной 6 (см.).
Решение
a=8a=8
b=10b=10
h=6h=6
Сразу подставляем числа в имеющуюся у нас формулу и вычисляем искомую величину:
S=a+b2⋅h=8+102⋅6=54S=frac{a+b}{2}cdot h=frac{8+10}{2}cdot 6=54 (см. кв.)
Ответ: 54 см. кв.
Формула площади трапеции по основанию и средней линии
Нужно упомянуть, что средняя линия трапеции равна половине суммы ее оснований. Тем самым, способ нахождения площади через среднюю линию есть не что иное, как способ, аналогичный первому. Поскольку:
l=a+b2,l=frac{a+b}{2},
то:
S=l⋅hS=lcdot h
ll — средняя линия трапеции;
hh — высота.
Найти площадь трапеции, если известно, что средняя линия равна 5 (см.), а высота трапеции в 2 раза больше её.
Решение
l=5l=5
h=2⋅lh=2cdot l
Найдем высоту трапеции:
h=2⋅5=10h=2cdot 5=10
Площадь:
S=l⋅h=5⋅10=50S=lcdot h=5cdot 10=50 (см. кв.)
Ответ: 50 см. кв.
Формула площади трапеции по всем сторонам
Данный способ подходит для тех случаев, когда в задаче известны все 4 стороны нашей трапеции.
S=a+b2c2−((b−a)2+c2−d22⋅(b−a))2S=frac{a+b}{2}sqrt{c^2-big(frac{(b-a)^2+c^2-d^2}{2cdot(b-a)}big)^2}
Даны длины всех сторон трапеции. Основания равны 10 (см.) и 5 (см.), боковые стороны: 4 (см.) и 3 (см.). Найти площадь фигуры.
Решение
a=5a=5
b=10b=10
c=4c=4
d=3d=3
Тогда:
S=a+b2c2−((b−a)2+c2−d22⋅(b−a))2=15216−(25+16−910)2=18S=frac{a+b}{2}sqrt{c^2-big(frac{(b-a)^2+c^2-d^2}{2cdot(b-a)}big)^2}=frac{15}{2}sqrt{16-big(frac{25+16-9}{10}big)^2}=18 (см. кв.)
Ответ: 18 см. кв.
Формула площади трапеции через диагонали и угол между ними
S=12⋅d1⋅d2⋅sin(α)S=frac{1}{2}cdot d_1cdot d_2cdotsin(alpha)
d1,d2d_1, d_2 — диагонали трапеции;
αalpha — угол между диагоналями.
Пусть две диагонали трапеции равны 20 (см.) и 7 (см.) и при пересечении они образуют угол 30 градусов. Найти площадь трапеции SS.
Решение
d1=20d_1=20
d2=7d_2=7
α=30∘alpha=30^{circ}
Площадь:
S=12⋅d1⋅d2⋅sin(α)=12⋅20⋅7⋅sin(30∘)=35S=frac{1}{2}cdot d_1cdot d_2cdotsin(alpha)=frac{1}{2}cdot20cdot 7cdotsin(30^{circ})=35 (см. кв.)
Ответ: 35 см. кв.
Формула площади трапеции через радиус вписанной окружности и угол
Этот случай подходит только для равнобедренной трапеции.
S=4⋅r2sin(α)S=frac{4cdot r^2}{sin(alpha)}
rr — радиус вписанной окружности;
αalpha — угол между основанием и боковой стороной.
Дан радиус вписанной окружности в трапецию, равный 4 (см.). Угол αalpha равный 90 градусам. Найти площадь трапеции.
Решение
r=4r=4
α=90∘alpha=90^{circ}
По формуле:
S=4⋅r2sin(α)=4⋅16=64S=frac{4cdot r^2}{sin(alpha)}=4cdot 16=64 (см. кв.)
Ответ: 64 см. кв.
Хотите заказать контрольную работу по геометрии? У нас самые низкие цены среди конкурентов!
Тест по теме «Площадь трапеции»
Усеченная пирамида – это многогранник, который образуется основанием пирамиды и параллельным ему сечением. Можно сказать, что усеченная пирамида – это пирамиду со срезанной верхушкой. Эта фигура обладает множеством уникальных свойств:
- Боковые грани пирамиды являются трапециями;
- Боковые ребра правильной усеченной пирамиды одинаковой длины и наклонены к основанию под одинаковым углом;
- Основания являются подобными многоугольниками;
- В правильной усеченной пирамиде, грани представляют собой одинаковые равнобедренные трапеции, площадь которых равна. Также они наклонены к основанию под одним углом.
Формула площади боковой поверхности усеченной пирамиды представляет собой сумму площадей ее сторон:
Так как стороны усеченной пирамиды представляют собой трапеции, то для расчета параметров придется воспользоваться формулой площади трапеции. Для правильной усеченной пирамиды можно применить другую формулу расчета площади. Так как все ее стороны, грани, и углы при основании равны, то можно применить периметры основания и апофему, а также вывести площадь через угол при основании.
Если по условиям в правильной усеченной пирамиде даны апофема (высота боковой стороны) и длины сторон основания, то можно произвести расчет площади через полупроизведение суммы периметров оснований и апофемы:
Давайте рассмотрим пример расчета площади боковой поверхности усеченной пирамиды.
Дана правильная пятиугольная пирамида. Апофема l = 5 см, длина грани в большом основании равна a = 6 см, а грань в меньшем основании b = 4 см. Рассчитайте площадь усеченной пирамиды.
Для начала найдем периметры оснований. Так как нам дана пятиугольная пирамида, мы понимаем, что основания представляют собой пятиугольники. Значит, в основаниях лежит фигура с пятью одинаковыми сторонами. Найдем периметр большего основания:
Таким же образом находим периметр меньшего основания:
Теперь можем рассчитывать площадь правильной усеченной пирамиды. Подставляем данные в формулу:
Таким образом, мы рассчитали площадь правильной усеченной пирамиды через периметры и апофему.
Еще один способ расчета площади боковой поверхности правильной пирамиды, это формула через углы у основания и площадь этих самых оснований.
Давайте рассмотрим пример расчета. Помним, что данная формула применяется только для правильной усеченной пирамиды.
Пусть дана правильная четырехугольная пирамида. Грань нижнего основания a = 6 см, а грань верхнего b = 4 см. Двухгранный угол при основании β = 60°. Найдите площадь боковой поверхности правильной усеченной пирамиды.
Для начала рассчитаем площадь оснований. Так как пирамида правильная, все грани оснований равны между собой. Учитывая, что в основании лежит четырехугольник, понимаем, что нужно будет рассчитать площадь квадрата. Она представляет собой произведение ширины на длину, но в квадрате эти значения совпадают. Найдем площадь большего основания:
Теперь используем найденные значения для расчета площади боковой поверхности.

Зная несколько несложных формул, мы легко рассчитали площадь боковой трапеции усеченной пирамиды через различные значения.